矩形通道局部变形堵塞对流传热实验研究

郭玖元邓永皓许 巍刘晓晶何晓强

1（上海交通大学 核科学与工程学院 上海200240）

2（中国核动力研究设计院 成都610041）

板状燃料元件因具有结构紧凑、传热效率较高等特点，被广泛应用于核反应堆中。板状燃料元件反应堆堆芯的冷却剂流道为狭窄的矩形通道，各通道间互不相通［1］。燃料包壳在长期的中子辐照和高温环境下可能会使矩形通道发生局部的肿胀、变形乃至鼓泡［2］，这将有可能引起冷却剂流道堵塞事故。

冷却剂流道堵塞事故会使得流道阻力增大、流量减少［3］，这可能造成燃料板失冷，板温升高，威胁包壳完整性，引发严重的事故后果。一些运行中的板状燃料反应堆已发生过此类事故，如1965年美国橡树岭研究堆发生过一起因橡胶垫片随冷却剂流入堆芯而引起的堵流事故，最终导致一个板状燃料组件中的三块燃料板局部熔化；1996年，Stovall等［4］开展了在冷却剂通道入口分别为25%部分堵塞和35%部分堵塞的实验研究，结果显示：流体在堵塞下游会存在一个流速降低区域，这导致了冷却剂通道内的流动传热能力降低，使得壁面温度升高；2014年，Li等［5］应用多维堆芯物理与热工水力耦合程序PORSTA的电动阀模型完成流道堵塞的瞬态模拟分析。结果显示：堆芯在发生流道堵塞事故瞬态会产生强烈的局部的物理热工负反馈效应，这使得堆芯局部功率下降。而从整个堆芯整体来看，反应堆的功率最终的变化趋势和堵塞份额有关；2014年，宋磊等［2］针对板状燃料组件在入口堵流事故下进行了数值模拟计算。计算结果显示即使达到95%的堵塞事故，甚至到全部堵塞，通道内部还是没有发生冷却剂沸腾现象，还发现在堵塞流道的内部的上游和下游存在旋涡区，在紧邻堵塞通道得到燃料元件表面出现了不同大小的高温区域。

目前对于矩形通道局部变形堵塞的流动传热实验研究，公开的文献报道极少，本文针对流道局部变形堵塞的情形，开展了低流量工况下实验研究，这将有助于分析实际局部变形堵塞对矩形通道流动传热的影响，对于了解反应堆的安全特性具有重要的意义。

1 实验装置

1.1 实验回路

实验装置示意图如图1所示。整个回路主要设备包括：水箱、隔膜计量泵、隔膜脉冲阻尼器、电磁流量计、电动调节阀、实验段、低压直流电源、热电偶数据采集器。实验装置的参数范围如表1所示。

表1 实验装置参数范围Table 1 Range of the paramenters

本实验在常压下进行，水泵将水箱的实验工质水泵出，水从实验段底部进入到加热的局部变形堵塞的矩形通道，经实验段的顶部出口后直接排出。

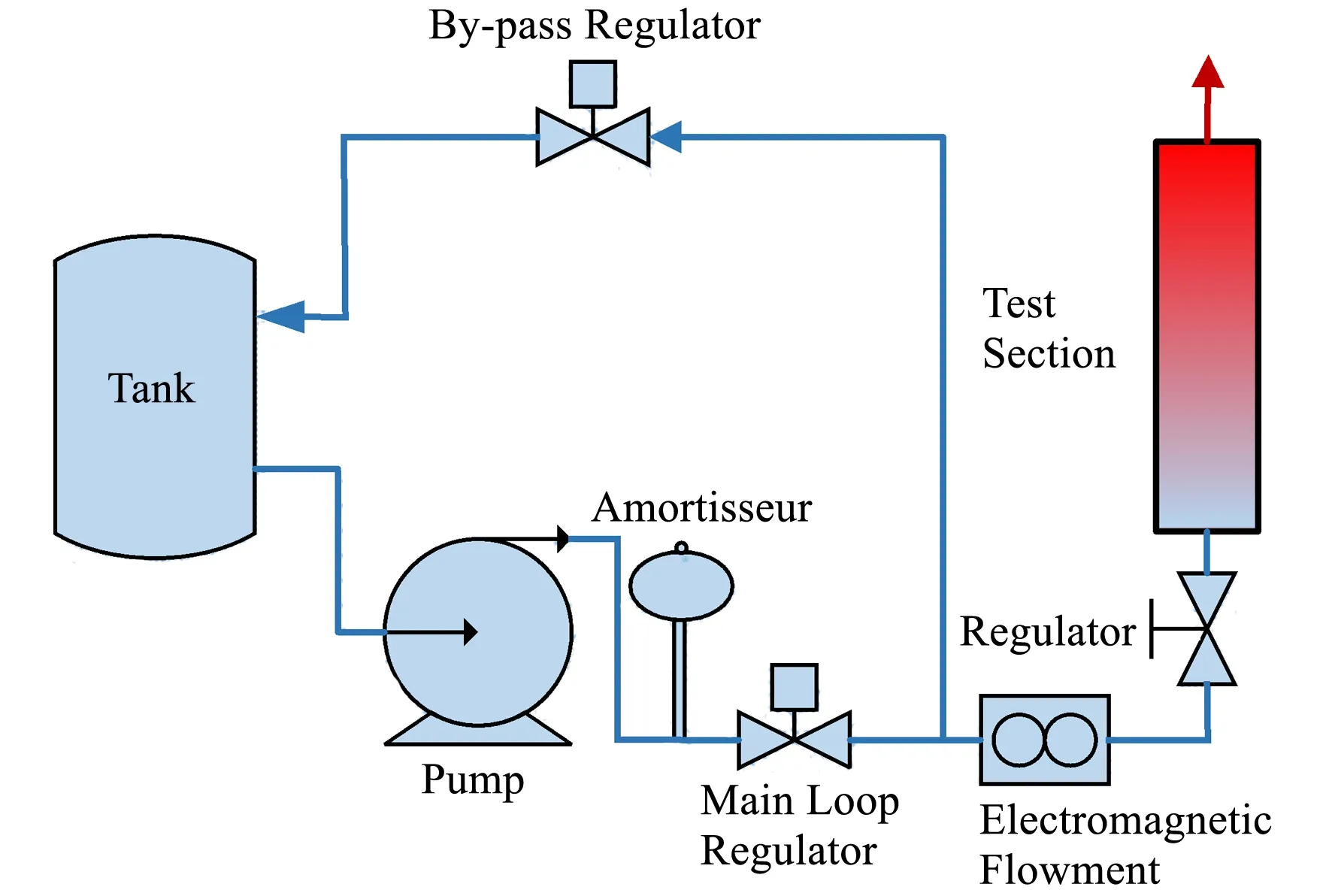
图1 实验装置示意图Fig.1 Schematic diagram of the experimental apparatus

1.2 实验段设计

实验段的主体是一块316L的不锈钢板，矩形通道的尺寸为宽60 mm、长600 mm、深3 mm。利用鼓泡结构模拟局部变形堵塞工况，参考了西屋公司设计的鼓泡结构［6］，本实验设计的鼓泡形状为球冠形状，如图2所示，球冠直径为7 mm，露出矩形通道的球冠高度hb是2.9 mm，鼓泡间距Sz为2 mm。设计了单鼓泡工况和无鼓泡工况分析鼓泡存在对换热的影响，并根据前期的数值模拟结果，选择了较为恶劣的横向三鼓泡，纵向三鼓泡分析鼓泡排列方式对换热的影响。

不锈钢板背部安装有Cr20Ni80电加热合金板，通过低压直流电源对电加热合金板通电对实验段单面进行加热，电加热合金板尺寸为长200 mm、宽60 mm，安装在实验段背面的正中央。实验段总长600 mm，在加热段上下区域各留有200 mm长非加热段，目的是使得流动更加稳定从而降低进、出口效应。图3是横向三鼓泡实验段的截面示意图。

图2 鼓泡示意图Fig.2 Schematic diagram of bubble

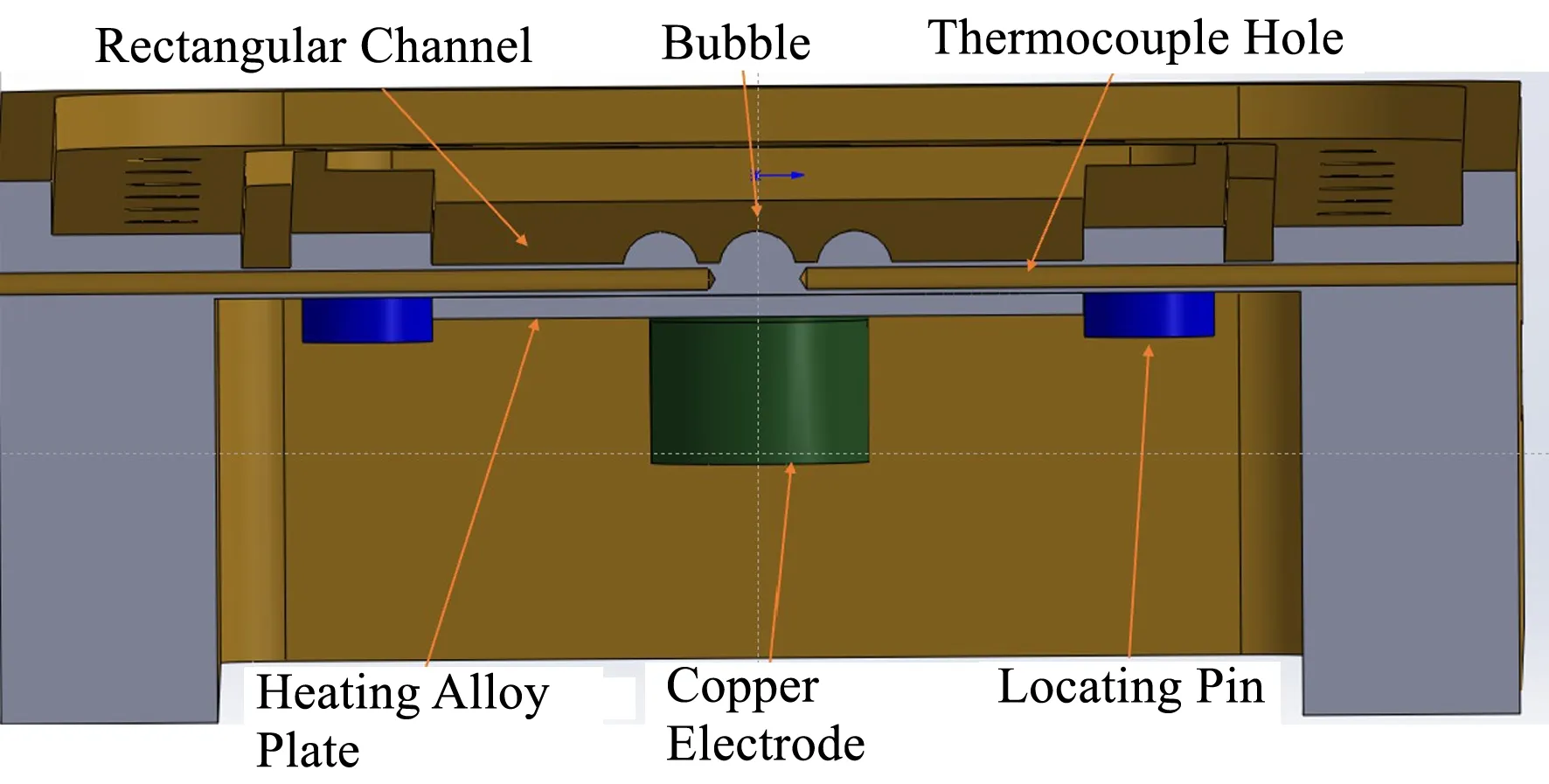
图3 横向三鼓泡实验段的截面示意图Fig.3 Cross section diagram of test section with transverse three bubbles

为防止电加热合金板的电流传导到实验段，影响到非接触式热电偶的数据采集的准确性，在电加热合金与实验段之间安装一块耐高温绝缘且易导热的氮化硼陶瓷垫片。热电偶从实验段侧面加工的孔插入测量温度，测点距离通道表面为0.5 mm。热电偶位置如图4所示，1号热电偶布置在下腔室，测量入口流体温度；9号热热电偶布置在上腔室，测量出口流体温度；2号、5号、6号、7号热电偶分别测量鼓泡右、下、左、上边缘的温度，4号、8号热电偶测量鼓泡来流和尾流的温度。

图4 热电偶位置示意图Fig.4 Schematic diagram of the thermocouples'location

2 实验数据处理

该实验通过间接加热对实验段进行加热，工质实际吸收的热量为Qh，由进出口处流体的比焓h的差值乘以体积流量V和工质密度ρ计算得到。

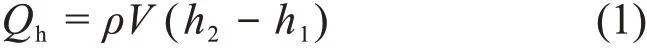
雷诺数Re根据式（2）计算：

式中：ρ为入口处流体密度；u取入口处流体平均速度；Dh为矩形通道的水力直径；μ为入口流体的动力粘性系数。

使用一维导热［7］推导出热电偶对应的壁面温度，并利用壁面温度平均值计算平均换热系数［8−9］，将2号、4号、5号、6号、7号、8号热电偶对应的壁面温度值取平均值，作为壁面温度平均值Tw［10］：

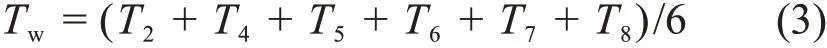
其中：Tf为主流区流体温度，取入口流体温度与出口流体温度的平均值［11］：

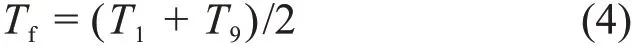
实验的平均努塞尔数Nue根据式（6）计算得到，计算导热率λ的定性温度取主流区温度Tf［12］：

通过处理实验数据，得到不同流速工况下的平均Nue数如图5所示。

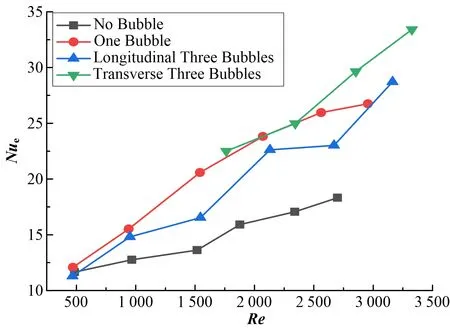
图5 不同实验工况平均Nue数对比Fig.5 Comparison of average Nusselt number of different cases

直接测量的参数体积流量和进出口流体温度以及壁面温度的最大不确定度分别为0.5%、0.4%、0.4%。实验段的加工精度为0.05 mm。采用Kline和McClintock的方法［8］，如式（7）所示，分析间接实验结果的最大不确定度，参数F是关于多个彼此相互独立的直接测量参数的函数。雷诺数的计算涉及到直接测量的参数实验段加工精度和体积流量V，努塞尔数的计算涉及到直接测量参数实验段加工精度、体积流量V、进出口流体温度T1、T9和壁面平均温度Tw和主流区温度Tf。

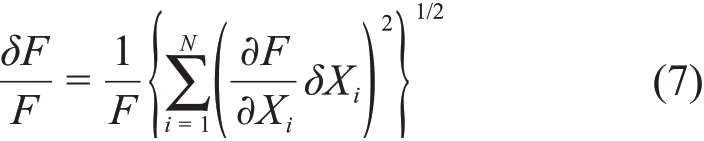
通过式（7）计算得出雷诺数Re和平均努塞尔数Nue的最大不确定度分别为1.69%和5.72%。

3 实验结果分析

根据图5所示的平均Nue数对比结果能够发现，在低雷诺数470～3 500内，各实验工况下的平均Nue数会随着Re而增大，流体对应传热能力也会随之增强；相同雷诺数下，鼓泡工况相对于无鼓泡工况，鼓泡的存在改变了鼓泡周围和下游位置的壁面热边界层的发展，突出的鼓泡诱发了涡流，加速了壁面附近流体的混合，这使得鼓泡附近的局部表面传热能力增强；相对于单鼓泡，横向三鼓泡的突出的鼓泡更多，影响流动的面积更大，对下游的影响更大，故对流动传热的影响更大；相对于单鼓泡，纵向三鼓泡在鼓泡间隙存在低速回流区，这一定程度上降低了流动传热能力，使得其流动传热能力在三种鼓泡工况中最弱。

国内外针对管道对流传热的研究比较成熟，适用于计算层流、过渡流、湍流的平均Nue且应用较广泛的相关对流传热关联式如表2所示。本实验工况大多在层流，因此选用齐德-泰特（Sieder-Tate）对流传热公式与实验数据进行对比分析。齐德-泰特公式如下：

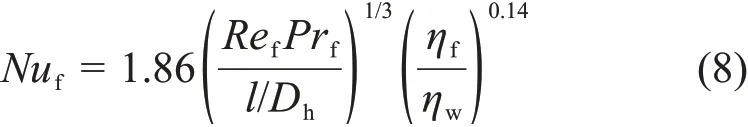
该公式考虑到入口段效应的层流传热，适用于计算长l的管道的平均努塞尔数，Prf为普朗特数，定性温度为流体平均温度Tf，特征长度Dh为水力直径，ηf、ηw分别为以流体平均温度和壁面温度定义的动力粘度。

表2 对流传热关联式对比Table 2 Convection heat transfer correlations

本实验工况是矩形通道局部变形堵塞，实验值与齐德-泰特的计算值之间存在一定的误差，通过将齐德-泰特公式计算出的平均Nuc数与实验平均Nue数对比，并计算其相对误差分别对不同实验工况的误差进行分析。

3.1 无鼓泡工况

从图6无鼓泡工况的误差图可以看出，无鼓泡工况的实验结果与齐德-泰特关系式的计算结果最大误差仅为14.8%，从而表明齐德-泰特关系式可用于计算矩形通道无鼓泡工况的对流传热。

而鼓泡工况下的实验结果与齐德-泰特关系式的计算结果的误差较大，由于鼓泡对矩形通道内流动的影响，使得对流传热强化，因此齐德-泰特关系式低估了矩形通道鼓泡工况的流动传热，通过对齐德-泰特关系式进行拟合修正，使得拟合修正后的关系式可以更准确地计算矩形通道鼓泡工况的流动传热系数。

3.2 鼓泡工况

鼓泡工况下，鼓泡突出的高度［16］以及排列方式对流动传热的影响明显［17］，对齐德-泰特公式进行拟合修正，通过对实验数据运用线性回归的方法拟合出反映Re的变化、球冠鼓泡的半径D、鼓泡突出的高度hb、鼓泡横向排布间距S1、鼓泡纵向排布间距S2与矩形通道水力直径Dh的流动传热关系式。

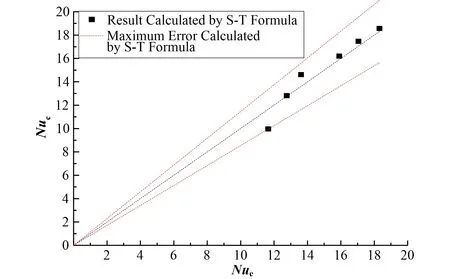
图6 无鼓泡工况公式计算平均Nuc数与实验平均Nue数误差图Fig.6 Diagram of the error between average Nusselt number calculated by the Sieder-Tate formula and the average Nusselt number calculated by experimental data in the case with no bubble

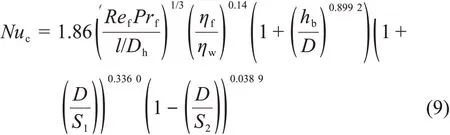
相比原来的齐德-泰特公式，修正公式中增加的含hb一项表示鼓泡突出高度对矩形通道传热的影响，增加的含鼓泡横向排布间距S1一项表示鼓泡横向排布时对矩形通道传热强化的效果，增加的含鼓泡横向排布间距S2一项表示鼓泡纵向排布时对矩形通道传热弱化的效果。

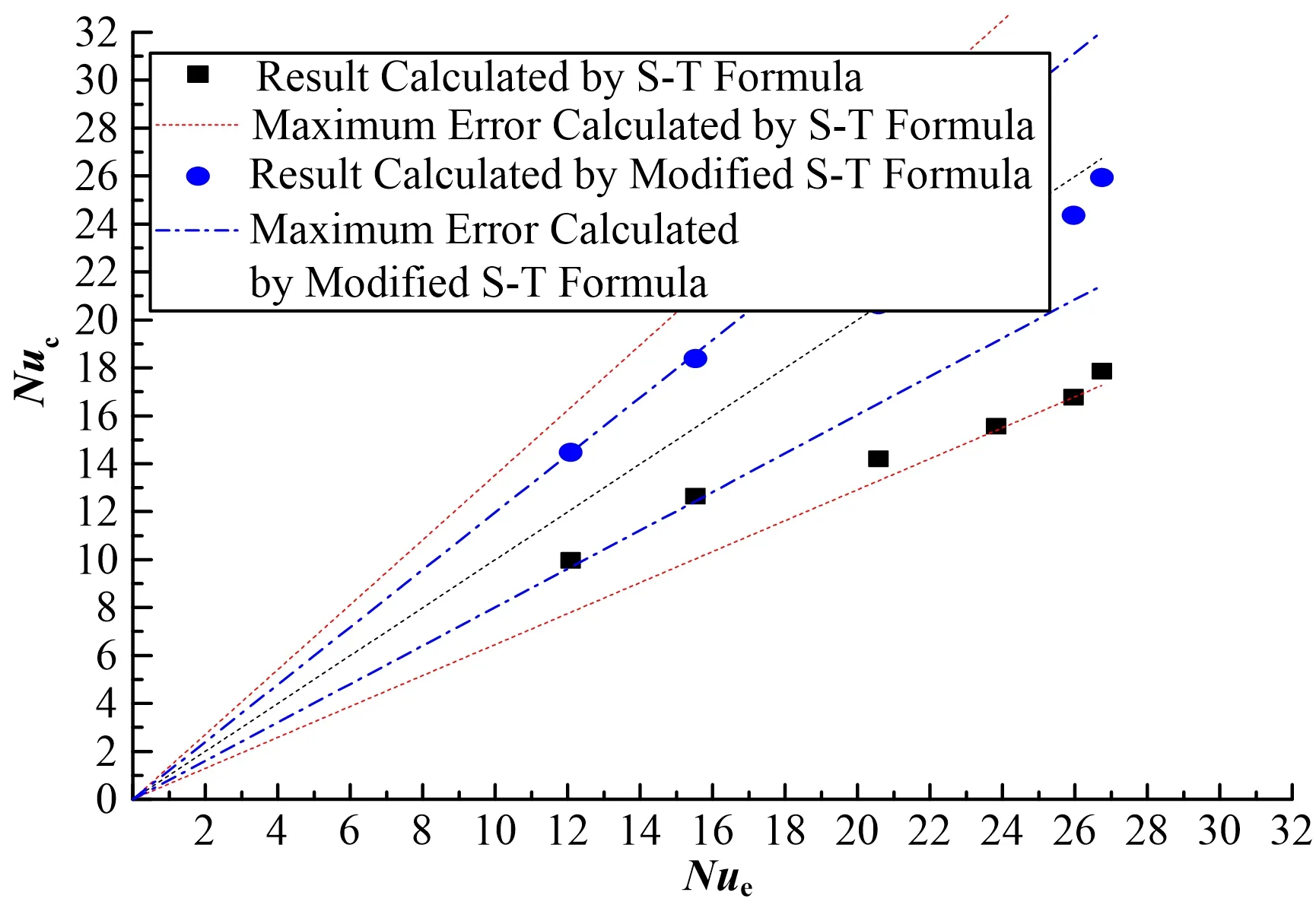
图7 单鼓泡工况公式计算平均Nuc数与实验平均Nue数误差图Fig.7 Diagram of the error between average Nusselt number calculated by the formula and the average Nusselt number calculated by experimental data in the case with one bubble

单鼓泡工况中随着Re增大鼓泡对对流传热的影响越来越大，齐德-泰特公式的计算值与实验值的相对误差越大，最大相对误差为35.4%。与原始公式相比，修正后的式（8）虽然高估了低雷诺数470～940工况的传热，但可以更准确地计算雷诺数1 500～3 000范围内的换热，而且修正公式与实验值的最大误差从原来的35.4%降至19.8%，可以更准确地计算单鼓泡工况下矩形通道内的对流传热系数。

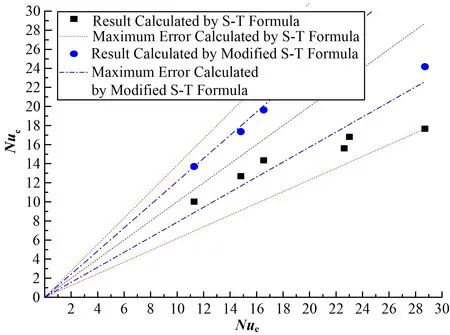
图8 纵向三鼓泡工况公式计算平均Nuc数与实验平均Nue数误差图Fig.8 Diagram of the error between average Nusselt number calculated by formula and the average Nusselt number calculated by experimental data in the case with longitudinal three bubbles

在纵向三鼓泡工况，在雷诺数470～1 540范围内，齐德-泰特公式与实验值的误差较小，随着雷诺数继续增大相对误差增大，最大误差出现在雷诺数3 160处，最大相对误差为38.5%。相对单鼓泡，纵向三鼓泡在鼓泡间隙存在低速回流区，弱化了其流动传热增强能力，所以修正公式的鼓泡个数n的指数为负值。修正后的公式虽然高估了雷诺数470～1 540工况的传热，但可以较好地计算雷诺数2 100～2 670的流动传热，修正后的公式最大误差从之前的32.8%降至21.3%，可以更准确地计算纵向三鼓泡工况下矩形通道内的对流传热系数。

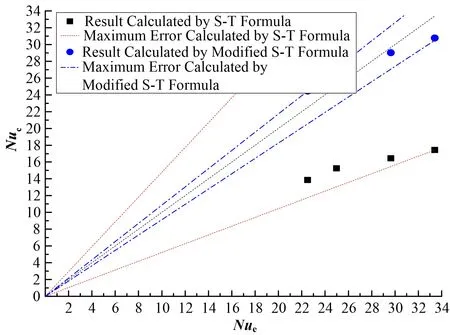
图9 横向三鼓泡工况公式计算平均Nuc数与实验平均Nue数误差图Fig.9 Diagram of the error between average Nusselt number calculated by formula and the average Nusselt number calculated by experimental data in the case with transverse three bubbles

由于横向三鼓泡对对流传热的增强效果最为明显，影响较大，齐德-泰特公式的计算值与实验值的相对误差较大，并且随着雷诺数而增大，最大相对误差在实验雷诺数最大3 300处达到47.8%。与原始公式相比，修正公式（9）与实验值的最大误差从之前的47.8%降至8.7%，可以更准确地计算横向三鼓泡工况下矩形通道内的对流传热系数。

4 结语

通过对矩形通道分别进行横向三鼓泡、纵向三鼓泡、单鼓泡三种局部变形堵塞工况和无鼓泡工况在低雷诺数400～3 300内的实验研究，得到以下结论：

1）随着实验工质的Re增大，矩形通道的平均Nue数增大。鼓泡诱发了涡流，破坏了热边界层地发展，使得流动传热增强，横向三鼓泡对传热增强最大，相对单鼓泡，纵向三鼓泡在鼓泡间隙存在低速回流区，弱化了其流动传热增强能力。

2）使用齐德-泰特公式计算矩形通道无鼓泡工况的平均Nuc数与实验的平均Nue数对比，最大误差仅为14.8%，从而表明齐德-泰特公式能够应用于计算矩形通道的对流传热。

3）考虑到鼓泡对流道对流传热的增强，分别对不同鼓泡工况对齐德-泰特公式的修正，单鼓泡工况修正后的公式的传热计算最大误差从35.4%降为19.8%；纵向三鼓泡工况修正后的公式的传热计算最大误差从38.5%降为21.3%；横向三鼓泡工况修正后的公式的传热计算最大误差从47.8%降为8.7%。修正的公式可以更加准确地计算矩形通道局部变形堵塞工况的对流传热系数。