基于偶然正确性概率的错误定位技术*

周小莉,赵建华

(计算机软件新技术国家重点实验室(南京大学),江苏 南京 210023)

1 引 言

软件测试是保障软件质量的一种重要而有效的手段,而软件的调试过程是测试中最耗时、最占据成本的任务之一.软件调试过程中,错误定位是最耗时和困难的一步[1].目前有许多自动化的错误定位技术,其中,基于代码覆盖的错误定位技术(coverage-based-faul-localization,简称CBFL)是实际开发中经常使用的一种自动化的错误定位技术[2-4],该方法通过比较成功用例和失败用例之间代码覆盖的差异,以对各语句的可疑度进行计算并排序.然而,基于覆盖的错误定位技术的有效性受到了偶然正确性现象的副作用的影响.偶然正确性现象是指程序中包含错误的语句被执行到但仍通过了测试的现象.许多研究已经证明偶然正确性现象是影响基于代码覆盖的错误定位技术有效性的主要因素之一[5],并且是降低成功测试用例的错误定位效能的最大影响因素[6].

不少研究工作都证明了偶然正确性现象在实际场景中是非常普遍的.偶然正确性现象的发生与如下两方面的因素有关:错误语句能否产生错误的中间结果以及错误的中间结果能否传递程序输出.在对西门子程序集的初步实验中,我们发现错误语句产生错误的中间结果的平均概率只有30%.而错误的中间结果能否传递到程序输出,与程序的信息流及其强度有关[7].在程序执行过程中,如果在某一程序点观测到的变量y的取值可以降低更早之前某一点上变量x取值的不确定性,则称从x到y产生了一个信息流.例如,顺序语句z=x+1;y=z/5 的执行将产生从x到y的信息流,而语句z=x+1;z=5;y=z/5 的执行将不产生从x到y的信息流.变量x和y之间的信息流强度表示已知y的取值的情况下变量x取值的不确定性的降低程度,信息流强度可在一定程度上反映变量取值之间的依赖程度.Masri 等人提出一种基于熵的方法来估量信息流强度,用熵对随机变量的不确定性进行量化,将变量x取值的不确定性与已知y取值时x的不确定性之间的差值作为x到y的信息流强度.偶然正确性现象是否发生,与错误语句所产生的中间结果能否将错误的中间状态传递到程序输出有关.因此,如果错误的中间结果与程序的输出之间不存在信息流或者强度比较弱,则很可能会发生偶然正确性现象[8].Masri 和Podgurski等人[7]对实际场景中信息流强度的统计结果表明,弱信息流是非常普遍的,甚至其中大多数信息流强度为0,这个结果也验证了其他工作中偶然正确性现象在实际场景中普遍发生的实验结果.

面向工程控制领域的软件(简称工控软件)被广泛地用于各种制造业以及电力、交通等国家关键基础设施,已成为国家安全战略的重要组成,对生产效率和安全性都有较高的要求.工控软件包含大量的控制过程,在执行时变量间的关联性不强,导致其信息流强度弱,使得偶然正确性现象更加频繁地出现在工控软件,从而对工控软件的错误定位产生了不良影响.

为了消除偶然正确性现象对工控软件等安全攸关软件的错误定位技术产生的影响,我们提出了一种基于偶然正确性概率的错误定位技术.该方法首先估算测试用例执行时发生偶然正确性现象的概率(coincidental correctness probability,简称CCP),然后基于偶然正确性概率对错误定位技术中可疑度的计算方法进行新的定义.本文采用了与我们以往工作[9]中类似的方法对偶然正确性概率进行估算,估计了各语句的执行实例对最终程序输出的影响程度.基于估算得到的偶然正确性现象发生概率,本文重新定义了错误定位中语句可疑度的度量方法,新的可疑度度量方法既考虑了代码覆盖,也考虑了偶然正确性现象对语句可疑度的影响.

本文第2 节介绍关于错误定位技术和偶然正确性现象的基本概念.第3 节对偶然正确性现象如何影响错误定位技术进行讨论,并介绍有关消除其副作用影响的相关工作.第4 节详细介绍基于偶然正确性概率的错误定位技术,包括偶然正确性概率的估算方法及可疑度的计算方法.第5 节介绍实验工作,将基于偶然正确性概率的错误定位技术与基于代码覆盖的错误定位技术进行对比.最后对本文工作进行总结.

2 基本概念

2.1 基于代码覆盖的错误定位技术

基于代码覆盖的错误定位技术是一种常用的自动化错误定位技术,其目标是发现被执行的代码中与错误有相关性的代码.该方法通过比较成功执行的用例和失败执行的用例之间代码覆盖的差异来为发现错误提供帮助.具有代表性的基于代码覆盖的错误定位技术有χSlice[10]、CBI(cooperative bug isolation)[11]、Tarantula[12]、Jaccard[13]和Ochiai[14]等技术.

基于代码覆盖的错误定位技术收集程序执行时的信息(包括语句执行覆盖信息和测试用例是否通过的信息),然后根据某种统计公式对各语句的可疑度进行计算并排序.语句的可疑度高表示其包含错误的可能性大,可疑度高的语句将被测试人员优先检查.基于代码覆盖进行错误定位的过程分为下面几个步骤.

(1) 对程序进行插桩,生成插桩后的可执行程序.

(2) 在插桩后的程序上执行测试用例集合,收集测试执行时的信息.对于每个测试用例,标记其是否通过测试,并获取对应的代码覆盖信息.在执行测试用例时,如果某条语句被至少执行过1 次,则标记该条语句被该测试用例所覆盖.

(3) 通过统计代码在成功和失败用例中被覆盖的比率来计算语句的可疑度,为测试人员提供一个需要被检查的语句集合,这个语句集合被称为语句检查集.

(4) 测试人员依次判断语句检查集中的每条语句是否包含错误.

这里,以Tarantula 方法为例展示对语句的可疑度进行度量的方法.Tarantula 方法是一种非常经典的错误定位方法,它是由Jones 等人于2005 年提出来的[15],Tarantula 方法的主要思想是相对于被更多成功测试用例所覆盖的程序元素,被更多失败测试用例覆盖的元素包含错误的可能性更高.在失败的测试用例中的覆盖率越大,程序元素越可能包含错误,可疑度越大.反之,程序元素在成功通过的测试用例中的覆盖比例越大,越可能是正确的语句,可疑度越小.本文将程序元素限制为程序中的语句.Tarantula 将语句s的可疑度度量定义为

当语句的可疑度相同时,使用另外一个度量值Confidence 来对语句进行排序:

计算出各语句的可疑度后,将语句按照可疑度取值从大到小进行排序,依次审查,直到找到错误语句为止.

Tarantula 技术取得了不错的错误定位效果,并且成为后续研究中被广泛使用和比较的技术.随后,Abreu 等人[13,14]提出了两种不同的可疑度计算公式:Jaccard 和Ochiai.其中,Jaccard 的可疑度计算公式受到聚类分析的启发,Ochiai 的可疑度计算受到分子生物学的启发.Ochiai 方法的效果相比Tarantula 有一定的提升.此外,Wong 等人[16]提出一种随着语句成功执行次数增加,其对可疑度贡献率逐渐减小的可疑度的计算方法.这种方法将语句成功执行的次数划分为3 个区间:[0,1]、[3,10]和[11,+∞].当语句的执行次数在区间[0,2]时,语句执行次数的贡献率权重为1,区间[3,10]的贡献率权重为0.1,区间[11,+∞]的贡献率仅为0.001.除了上述可疑度计算公式以外,还存在许多不同的可疑度计算公式[17-19].

为了衡量错误定位技术的有效性,可以用下面两个指标对其进行评估.

(1) 安全性变化

安全性表示错误代码的相对可疑度.假设f是实际包含错误的语句,使用score(f)表示根据错误定位方法计算出的f的可疑度值,T是被用来进行错误定位的测试集合.将安全性定义为下面这个集合的大小[20].

由定义可知,S(T)是大于或等于score(f)的不同的可疑度取值的集合.分别用S(T)和S＇(T)表示基于偶然正确性概率的错误定位技术和Tarantula 计算出的可疑度不低于score(f)的可疑度值的集合.如果|S(T)|＞|S＇(T)|,表明基于偶然正确性概率的技术提高了错误定位的安全性;如果|S(T)|=|S＇(T)|,表明错误定位的安全性保持不变;如果|S(T)|＜|S＇(T)|,表示基于偶然正确性的技术降低了错误定位的安全性.

(2) 精确度变化

精确度代表定位到错误语句所需的代码检查代价.假设R为比错误语句的可疑度高的语句的数目,R值越高,表明找到错误语句的代价越大.反之,R值越低,找到错误语句的代价越小.如果一种错误定位技术使得R值变小了,则认为该方法提高了精确度.精确度的变化可以用错误语句的排名直观地观测到.

2.2 偶然正确性现象

对于基于代码覆盖的错误定位技术,如果一个测试用例执行了包含错误的语句,却没有产生错误的程序输出,此时这个用例对错误定位没有贡献,甚至对可疑度的计算产生负面的影响.这种错误语句被执行却没有产生错误结果的现象称为偶然正确性现象.

偶然正确性现象是指程序中发生了错误但仍通过了测试的现象.最初,偶然正确性的概念是由Budd 和Angluin[21]提出来的.Masri 使用PIE(propagation-infection-execution,传播-感染-执行)模型对偶然正确性现象进行了定义[20].Voas 于1992 年提出的PIE 模型[22]强调了程序缺陷的执行并不是程序失效的充分条件,还需要满足将错误的中间状态传播到程序的输出中.Ammman 和Offutt 提出的RIP(reachiability-infection-propagation,到达-感染-传播)[23]模型中再次讨论了这个问题.Voas 指出当且仅当满足下面3 个条件时错误才会被观测到.

执行(execution),错误代码需要被执行到;

感染(infection),执行错误代码时必须触发一个错误的中间状态;

传播(propagation),这个错误的中间状态必须能够传播到程序的输出,使得我们能够观测到它与预期的输出不一致,即失效.

Masri[8]将偶然正确性现象进一步分类为强偶然正确性现象和弱偶然正确性现象.强偶然正确性现象发生在“执行”和“感染”两个条件被满足而“传播”条件没有被满足时.若“执行”条件被满足而“传播”条件没有被满足,则无论“感染”条件是否被满足,都称发生了弱偶然正确性现象.许多工作都证明了偶然正确性现象的普遍性[5,8,24],尤其弱偶然正确性现象的发生是非常频繁的[8].

2.3 偶然正确性现象对错误定位技术的影响

许多研究工作[5,6,24]都证明偶然正确性现象对错误定位的有效性带来了副作用影响.Denmat 等人[25]对经典的基于代码覆盖的错误定位技术Tarantula 的局限性进行了研究,并表明要使其有效,必须满足错误语句的执行在大多数情况下会导致程序出错,即大多数程序的执行中不会发生偶然正确性现象.Masri 等人[5]对降低基于代码覆盖的错误定位技术有效性的因素进行了实验性研究,结果表明,偶然正确性现象普遍存在,并且是影响基于覆盖的错误定位技术有效性的主要因素之一.另外,Lei 等人[6]对测试用例的错误定位效能进行了分析和总结,证明偶然正确性现象是影响成功测试用例的错误定位效能的最主要的因素.

Table 1 Suspiciousness metrics of three CBFL techniques表1 3 种基于覆盖的错误定位技术的可疑度计算公式

本文从偶然正确性现象对各语句的可疑度计算产生的具体影响的角度出发,讨论偶然正确性现象如何影响错误定位技术的有效性.我们以Tarantula、Jaccard、Ochiai 这3 种流行的基于代码覆盖的错误定位技术为例,分别比较考虑和忽略偶然正确性现象所计算出的可疑度.对于一个语句s,分别用s00、s01、s10、s11表示4 类测试集合的用例数目.

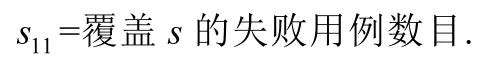
测试集合的这些属性将用来计算语句的可疑度度量.在表1 中展示了Tarantula、Ochiai 和Jaccard 这3 种错误定位技术的可疑度度量的计算公式.假设在测试集合中有n个测试用例发生了偶然正确性现象.这里,使用M(s)和M＇(s)分别来表示忽略和考虑偶然正确性现象的可疑度度量.

首先以Tarantula 为例来展示可疑度的计算.假设s是包含错误的语句,在全部测试用例中有n个测试用例发生了偶然正确性现象,也就是说有n个测试用例覆盖了语句s但并没有产生错误的结果.这种情况下,M(s)的值被错误地估计了,为了得到更精确的值,需要将n个测试用例从s10中去掉,新的可疑度度量M＇(s)的值为

显然地,M＇(s)＞=M(s),也就是说,如果不考虑发生偶然正确性现象的测试用例将低估错误语句s的可疑度.并且,随着n的增大,M＇(s)的值也会相应增大.也就是说,在估算语句s的可疑度时,覆盖语句s且因为偶然正确性而通过测试的测试用例个数越多,则可疑度估算的误差越大,从而对错误定位的安全性和准确性造成影响.因此,针对该语句的可疑度估算需要做出不同程度的修正,以得到能够更加准确地反映出语句中包含错误的可疑度排序.

对于Ochiai 和Jaccard,可用相同的思路估计偶然正确性现象对可疑度的影响,需要将n个发生偶然正确性现象的测试用例从s10中抽出,以得到一个修正的可疑度度量值.对于Ochiai,考虑了偶然正确性现象的可疑度为

对于Jaccard,考虑偶然正确性现象的可疑度公式为

同样地,对于Ochiai 和Jaccard,考虑了偶然正确性现象所估算的可疑度值也是大于或等于原本公式计算出的可疑度值.实际执行中发生偶然正确性现象的测试用例越多,其可疑度估算的误差也越大,因而对错误语句的可疑度排序的准确性产生影响.

3 偶然正确性现象的相关工作

Masri 等人[20]围绕偶然正确性现象的定义、分类和产生原因进行了研究,并对其在实际场景中出现的频率进行了实验.Daran 等人[24]在对实际场景中出现的错误进行分析时,也验证了偶然正确性现象的普遍性.

目前,偶然正确性现象的相关工作大多集中在错误定位方向.Masri[5]、Yei[6]和Denmat[24]等人的研究工作都证明了偶然正确性现象是影响基于代码覆盖的错误定位技术有效性的主要原因之一.随后,许多研究工作试图消除偶然正确性现象对错误定位技术产生的副作用影响.这些工作通常使用两种不同的策略消除偶然正确性的影响,第1 种策略是直接将发生偶然正确性现象的用例从测试集中删除,另一种策略是将发生偶然正确性现象的用例归类为失败用例.其中,最大的挑战是如何判断测试过程中是否发生了偶然正确性现象.

Masri 等人[8,20]提出了多种识别发生偶然正确性的测试用例的方法,这些方法大多基于一个类似的思想,即发生偶然正确性现象的测试用例是与失败用例有着相似行为的成功用例.Masri 等人[20]通过聚类分析来识别偶然正确性现象,其采用的聚类算法是K-均值聚类算法.首先,将测试用例使用欧式距离计算类间距离并进行聚类,将原始测试集合聚类为两个类簇.然后,选取包含更多的失败用例的类簇,将该类簇中的成功用例识别为发生偶然正确性现象的用例.然后,Masri 在Tarantula 技术的基础上,将发生偶然正确性现象的用例删除后再进行错误定位.另外,Marsi 等人[8]还提出一种基于散点图来识别偶然正确性用例的方法.这种方法将散点图上两个测试用例间直接的距离作为两者的不同程度,将与执行失败的用例最接近的用例识别为偶然正确性用例.

基于与上述方法类似的思想,一些基于聚类的识别偶然正确性用例的方法被提出[26,27].陈振宇等人[23]提出了一种基于聚类分析的方法来消除偶然正确性现象对错误定位技术的影响.Li 等人[27]提出了对谓词信息进行聚类分析来识别偶然正确性用例的方法.孙召倩等人[28]在聚类分析算法的基础上引入了模糊概率算法,将一个成功测试用例是偶然正确性用例的概率设置为0 到1 之间的取值,降低了识别偶然正确性用例的误报率和漏报率.此外,Wang 等人[29]使用带上下文模式的覆盖度重定义方法来消除偶然正确性现象对Tarantula 技术的影响.这种模式从程序的数据依赖和控制依赖关系的角度出发,认为如果错误可以被发现,那么一定有与之相匹配的上下文模式.Wang 等人总结了12 个上下文模式,可以对实际开发中常见的13 种类型的错误进行匹配.然而,实际开发场景中程序包含的错误类型远不止13 种,因此这种方法具有一定的局限性.另外,张卓等人[30]提出了一种增强上下文的错误定位方法,该方法关注失败测试用例,通过动态切片提取更精确的信息,缩小错误搜索范围,抑制了发生偶然正确性现象的成功用例对错误定位结果产生负效应的空间,间接地缓解了偶然正确性问题.同时,张卓等人也指出这种方法无法彻底消除偶然正确性现象的影响.

另外，偶然正确性现象在测试充分度和边界值分析方面也引起了一些研究关注.基于代码覆盖的测试充分度是在测试中最常用的测试充分度准则,然而代码覆盖和错误发现之间并没有很强的相关性.偶然正确性现象是导致代码覆盖无法准确表示测试充分程度的主要原因之一.在以往的工作[9-31]中,我们提出了一种估算程序执行时发生偶然正确性现象的概率的方法,并基于偶然正确性概率对测试充分度进行衡量.相对于基于代码覆盖的测试充分度,基于偶然正确性概率的测试充分度与错误发现之间有更强的相关性,更能准确地反映测试的充分程度.偶然正确性现象对边界值分析也产生了副面影响.Hierons[32]对发生偶然正确性现象的实例进行了研究,并提出了一种生成不发生偶然正确性现象用例的方法.

4 基于偶然正确性概率的错误定位技术

基于代码覆盖的错误定位技术是通过语句在成功和失败用例中被覆盖的比率来对其可疑度进行计算的.然而,这个比率的计算会因为偶然正确性现象发生而产生误差,需要根据偶然正确性现象对可疑度加以修正.

在以往工作[9]中,我们提出一种对测试用例执行时发生偶然正确性的概率进行估算的方法.基于偶然正确性现象的发生概率,本文将测试用例部分地分类为失败用例和成功用例,从而对可疑度的计算进行修正.下文首先介绍偶然正确性概率估算方法,然后详细给出利用偶然正确性概率对可疑度进行度量的方法.

4.1 偶然正确性概率的估算

偶然正确性概率的估算[9]是本文工作的基础,本文从代码执行过程中内存空间变化的角度出发,通过动态的数据流和控制流两个方面来估算程序执行过程中发生偶然正确性的概率.程序的执行过程可以看作这些语句实例对内存空间中值进行读取、计算和写入的过程.通常根据检查程序输出来判断是否通过了测试,因此包含错误的程序在一次执行中发生偶然正确性概率可以看作在该错误执行后程序仍然产生正确输出的概率.

偶然正确性现象发生在包含错误的语句被执行但是没有产生错误的中间值时,或者错误语句产生了错误中间值却没有将错误的中间状态传递到输出中的时候.错误的中间值没有被传递到输出的原因是这个错误中间值没有被用来生成最终的输出,或者错误中间值在产生程序输出前被掩盖.这里的掩盖可能是错误的值被后续语句的赋值所直接覆盖,也可能是参与运算,却偶然地产生了正确的运算结果.例如,假设错误语句s的执行为变量x进行了错误的赋值,如果x与值为False 的操作数进行并运算,或者与值为0 的操作数进行乘法运算,此时运算结果仍然是正确的,x中的错误会被掩盖.再比如,x被用于比较运算中,虽然x的值是错误的,但与正确的取值在同一区间,那么比较运算的结果仍是正确的.

本文从运算和控制流两方面来估计错误的中间状态被传播到程序输出的概率.

(1) 运算的影响

运算的影响是估计错误的中间结果被计算性使用时对运算结果产生的影响.例如,当错误的中间值被用于赋值语句表达式、输出语句或当作函数调用的参数以及被用于索引表达式中时,通常会得到错误的运算结果,但也仍然可能是正确的运算结果,这也是偶然正确现象出现的原因之一.运算结果的正确性与操作数的正确性和所参与的运算有关.如果操作数的取值都正确,那么运算结果也一定是正确的;如果至少一个操作数是错误的,那么运算结果也很可能是错误的.对于不同的运算和操作数的取值,操作数对运算结果正确性的影响程度也不同.对不同类型的运算,本文通过为每个操作数都设定不同的影响因子来量化该操作数对运算结果正确性的影响程度.运算结果的正确性概率可以根据运算的类型、操作数的正确性概率以及其当前的取值进行估计.

(2) 控制流的影响

控制流的影响是指错误的中间结果被判定性使用时所产生的影响.当错误的中间结果被用于分支语句的条件表达式时,会导致程序错误地执行了某条路径,被实际执行的路径上和应该被执行的路径上的语句所改变的变量的值,其正确性都受到了影响.由于未被执行的路径信息难以获取,这里只考虑被执行的分支内所涉及的内存单元的正确性.对于一条语句实例s,为了估算控制流对其结果正确性概率的影响,我们首先找到影响s的所有控制表达式的执行实例,然后根据这些表达式的正确性概率对s的结果的正确性概率进行修正.

对于程序中的任意一个语句s,通过分析s的各个实例产生的中间结果直接或间接传播到输出的过程,可以估计出s的执行对程序输出的影响程度.这里,我们将程序输出不受到s的执行影响的概率定义为CCP(s,t),这一概率同时也是假定s中包含错误的前提下此次执行的输出结果的正确性概率,即发生偶然正确性现象的概率.

对于一个测试用例,错误所在的位置不同(即包含错误的语句不同),其执行时对程序输出的影响程度也有所不同.因此,为了估计程序的一次执行发生偶然正确性现象的情况,我们对每一条语句都进行分析,估算它的执行对程序输出的影响.本文所使用的估算方法是针对每个测试用例和程序中每条语句进行估算,可以比较精细地分析出偶然正确性现象发生的情况.

4.2 基于偶然正确性概率的可疑度计算方法

本文在Tarantula 的基础上,根据偶然正确性概率对其可疑度的计算公式进行修正,从而得到一个基于偶然正确性概率的可疑度度量方法.Tarantula 是一种非常经典的基于代码覆盖的错误定位技术,在错误定位相关研究中被广泛使用和比较.同时,其他消除偶然正确现象对错误定位影响的相关研究工作[8,26,30]也都是在Tarantula的基础上进行修正的.本文提出对可疑度的修正方法同样可以用于Jaccard 等基于代码覆盖的错误定位技术上.

为了计算语句s的可疑度,Tarantula 方法根据测试用例是否覆盖s以及是否通过测试将测试用例集合分成4 个互不相交的子集,用s00、s01、s10和s11分别表示这4 个集合的元素个数.其中,s00表示未覆盖语句s的成功测试用例的数目,s01表示未覆盖s的失败用例数目,s10表示覆盖s的成功测试用例数目,s11表示覆盖s的失败测试用例数目.

本文提出的错误定位技术不是将测试用例简单地归入到上述某个集合中,而是根据偶然正确性概率按照一定比例将测试用例“部分”分配到上述集合中.这里,用f00(s,t)、f01(s,t)、f10(s,t)和f11(s,t)分别表示测试用例t被“部分”分配到这4 个子集中的值,则有,

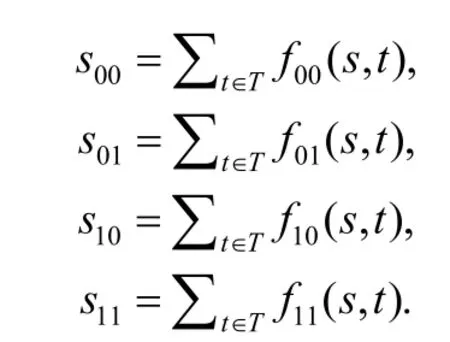
这里,将s00、s01、s10和s11称为FPValue变量,将f00(s,t)、f01(s,t)、f10(s,t)、f11(s,t)称为FPValue增量函数.对于语句s和测试用例t,首先估算出偶然正确性概率CCP(s,t),然后根据CCP(s,t)对FPValue增量函数进行计算.这里的CCP(s,t)并不是测试用例t在实际执行时发生偶然正确性现象的概率,而是在假设s包含错误的情况下执行t时发生偶然正确性现象的概率,即t执行时程序输出不受到s执行时所产生的影响的概率.

基于代码覆盖的错误定位技术认为,如果语句被失败用例覆盖得越多、被成功用例覆盖得越少,其可疑度就越高.这类技术有一个潜在的假设:错误语句被覆盖时很可能会产生错误的程序输出,而错误语句没有被覆盖时则很可能产生正确的输出.当语句s的执行对t执行时的程序输出没有任何影响时,从错误定位的角度考虑来看,相当于s没有被执行到.表2 中给出了根据CCP(s,t)计算FPValue增量函数的方法,将测试用例分为4 种情况进行分析.

(1) 如果t是覆盖语句s的成功用例,语句s有CCP(s,t)的概率对程序的输出不产生影响,因此,将该用例CCP(s,t)的概率分配到未覆盖且成功用例集合中,1-CCP(s,t)的概率分配到覆盖且成功用例集合中.

(2) 如果t是覆盖s的失败用例,此时用与第1 种情况类似的方法进行分配.语句s有CCP(s,t)的概率不对程序的输出产生影响,因此,将该用例以CCP(s,t)的概率分配到未覆盖且失败用例集合中,以1-CCP(s,t)的概率分配到覆盖且失败用例集合中.

(3) 如果t是未覆盖语句s的失败用例,则将其归类到未覆盖且失败用例,即f01(s,t)=1,其他FPValues函数的值为0.

(4) 如果t是未覆盖语句s的成功用例,则将其归类为未覆盖的失败用例,即f00(s,t)=1,其他FPValues函数的值为0.

Table 2 The calculation of incremental functions of FPValues表2 FPValues 增量函数的计算

本文只考虑了前两种情况下语句s的偶然正确性概率.其他两者情况下,语句s的偶然正确性概率与错误定位的关联并不大,因此可疑度的计算方法与原始的Tarantula 方法相同.对于前两种情况,在CCP(s,t)=0 这种极端情况下,如果t包含错误,它的执行一定会导致程序出错,此时,FPValues函数的计算方法将退化为Tarantula 中的计算方法.如果CCP(s,t)的值非常高,测试用例t对程序输出的影响非常小,本文提出的方法倾向于将测试用例t更多地放入未被覆盖的测试用例集合中.本文按照偶然正确性概率对测试用例重新划分,从而消除了偶然正确性现象对可疑度计算的影响.

5 实验评估

5.1.1 目标程序和实验设计

西门子程序集被广泛地应用于评估各种测试技术有效性的实验工作上,也是偶然正确性现象相关工作[7-9,20]中经常使用到的目标程序.在实验中,本文从SIR 中获取了西门子程序集的7 个合适大小的C 程序,其中包含了62 个错误版本的程序,每个错误版本程序中只包含1 个错误.表3 提供了目标程序的基本信息和配套的测试用例集合,包含了源程序代码的大小、测试用例的数目以及失败的测试用例的数目等信息.

Table 3 Subject programs表3 目标程序

实验中将基于偶然正确性概率的错误定位技术与Tarantula 技术进行比较,统计其错误定位结果安全性精确度的变化,并与相关工作[8]的结果进行对比.对于每一个版本的程序,按照下面几个步骤进行实验.

(1) 获得预备信息

首先,根据执行结果将测试用例集合分类为执行成功和执行失败两种用例.然后,找到并标记包含错误的语句.对于每一个测试用例,标记是否覆盖了包含错误的语句.

(2) 估算偶然正确性概率

对于每一个语句s和每一个成功执行的测试用例s,计算CCP(s,t)的值,即假设s为错误语句时测试用例t因为偶然正确性现象而被通过的概率.

(3) 计算可疑度

对于每一个语句,分别使用Tarantula 和基于偶然正确性概率及代码覆盖的错误定位技术来计算可疑度.对于每个版本的程序,分别统计其错误定位结果的安全性和准确性的变化情况.

5.1.2 实验结果和分析

本文对目标程序执行时发生偶然正确性现象的频率进行了统计,并将基于偶然正确性概率的错误定位方法与Tarantula 的错误定位结果的安全性和精确度进行对比.

(1) 偶然正确性现象的发生频率

在实验中将覆盖了错误语句的被通过用例归类为偶然正确性用例.图1 展示了偶然正确性用例的统计信息,图中将错误版本的程序按照原始程序进行了分组显示,其横坐标是原始程序,纵坐标为这个程序的所有变种程序所对应的测试集合中偶然正确性用例所占的平均比例,即偶然正确性现象出现的平均频率.对于所有原始程序的错误版本,其偶然正确性现象发生的平均频率都超过20%,其中对于“schedule2”的变种程序,偶然正确性现象的平均概率甚至高达90%以上.对图中的数据作进一步的统计后发现,偶然正确性现象在所有目标程序执行中出现的平均频率为53%.很明显地,偶然正确性现象在目标程序中非常频繁地出现.

(2) 错误定位结果的对比

在实验中,本文将基于偶然正确性概率的错误定位方法与Tarantula 在错误定位的安全性和精确度上进行了对比.图2 和图3 展示了错误定位的安全性和精确度的变化情况.图2 中将所有错误版本的程序按照原始程序进行了分组显示,图中的横坐标是原始程序,纵坐标为这个程序的所有变种的错误版本中其错误定位结果的安全性和精确度有所提高或保持不变的程序版本的比例.在图3 中展示了关于精确度变化的更详细的信息,其中,横坐标代表不同的程序版本,纵坐标表示精确度的变化.从图2 和图3 中可以看出,基于偶然正确性概率的错误定位技术在安全性和精确度上均得到了一定的提升.

(a) 安全性方面

从图2 中可以看出,错误定位的安全性被提升的程序版本比例在75%～100%之间.对图上所有程序进行综合统计后发现,对于95%的程序,其错误定位的安全性都得到了提升,其他5%的程序(只有3 个程序版本)维持了原有的错误定位的安全性指标,没有任何程序的安全性被降低.这个实验结果表明,对于所有版本的程序,基于偶然正确性的错误定位技术都提高或维持了错误定位的安全性.

(b) 精确度方面

精确度表示搜索到错误语句所付出的代价,它是衡量错误定位有效性的最重要的指标.如图2 所示,错误定位的精确度得到提升或者保持不变的程序所占的比例在66.67%～89.47%之间,其他程序的错误定位的精确度被降低.如果考虑精确度不变的情况,那么,维持或者提升精确度的比例为66.67%～89.47%之间.对于所有版本的程序,其精确度变化的综合结果是错误定位的精确度平均被提升了3.77%.其中,对于77.42%的程序,基于偶然正确性概率的错误定位技术得到了精确度的提升,其平均上升幅度为5.3%.对于19.35%的程序,错误定位的精确度有所下降,其平均下降幅度为1.9%.对于另外3.22%的程序,其错误定位的精确度保持不变.

Fig.1 Percentage of coincidental correctness tests图1 发生偶然正确性现象的用例所占的比例

在实验中,实际执行时发生偶然正确性概率高的程序在精确度上的表现相对优于其他程序,这也说明,我们的方法可以有效地消除偶然正确性现象对错误定位的影响.发生偶然正确性现象频率较低的程序在错误定位精确度上的表现上略劣于其他程序,这是因为,消除偶然正确现象的影响对其定位结果的提升是有限的.另外,某些程序在精确度上被降低的原因可能与偶然正确现象概率的估算值与实际的差异有关.

精确度相关的实验结果表明,对于大多数版本的程序,基于偶然正确性概率的错误定位技术提高了出错语句在可疑语句序列中的排名,使得错误可以更早地被测试人员所定位到.对于小部分版本的程序,出错语句的排序下降了,但其下降程度相对较小.总体而言,本文提出的错误定位技术一定程度上提高了错误定位的精确度.

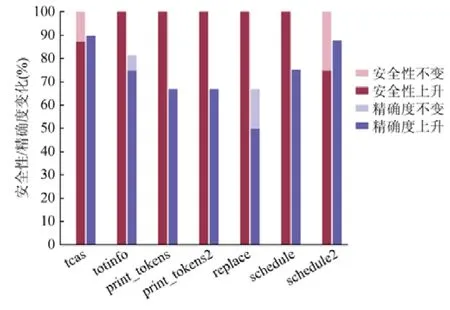
Fig.2 Changes of safety and precision图2 安全性和精确度的变化

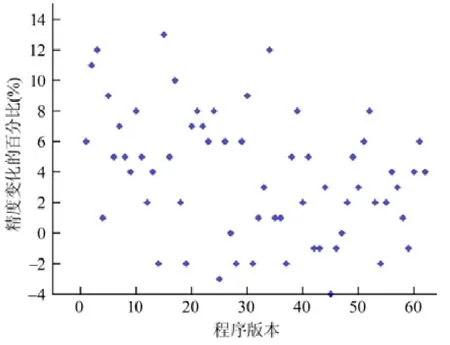
Fig.3 Deatals of precision changes图3 精确度变化的详细信息

(c) 与相关工作的对比

在相关工作中,Masri 等人[8]提出了多种提高错误定位技术有效性的技术,并在西门子程序集中的18 个版本的程序上进行了实验.在这项工作中,达到最优效果的技术(系数为0.8 的技术3)对于80%的程序提高了错误定位的安全性,对于61%的程序提高了错误定位的精确度.本文在实验中所选取的程序包含了文献[8]的工作中所用的目标程序,我们的方法提高了95%的程序定位结果的安全性,提高了77%的程序定位结果的精确度.相对于Masri 的方法,本文提出的方法在安全性和精确性上都有一定的优势.

基于与Masri 工作[8]类似的思想,另有一些使用聚类方法来消除偶然正确性现象影响的研究.为了保证聚类分析的效果,这些工作选取了较大规模的程序进行实验,而没有选取西门子中常用的小规模程序,与本文选取的目标程序不同,所以不能直接与我们的实验结果进行对比.在这些基于聚类的工作中,Li 等人[30]的在错误定位上的实验结果较优,这种方法对偶然正确现象识别的误报率较低(平均值为4.85%),而漏报率较高(平均值为47.4%).Li 等人[30]在实验中用精确度变化来衡量错误定位技术有效性的提升情况.他们通过对测试用例重新划分的方法使得84.5%的程序的错误定位的精确度得到提升或保持不变,其提升程度为6.15%,另外,15.5%的程序的定位结果的精确度降低,其降低程度为1.5%.其他基于聚类的方法也存在部分程序的定位结果变差的情况.这些基于聚类的方法与Masri 的工作有一定的相似性,其有效性很大程度上受到程序规模和测试集合大小的影响,如果目标程序的规模过小,那么会导致程序执行剖面的数据维度过小,使得测试用例之间的相似性过大,最终聚类算法难以分辨出测试用例之间的区别.如果测试集合太小,聚类分析得到的数据过少,也无法得到比较好的识别效果.

6 总结

偶然正确性现象是指包含错误的语句被执行却产生了正确的程序输出的现象,在程序执行过程中普遍存在.偶然正确性现象被证明是影响错误定位技术有效性的主要因素之一,因此亟需一种有效的方法消除偶然正确性现象对错误定位技术的影响.以往的研究工作多数使用聚类等方法找到与失败用例具有相似行为特征的用例,将其作为发生偶然正确性现象的用例从测试集合中删除,或者将其归类为失败用例.与上述研究工作不同,本文关注错误的值是如何产生并被传播到程序的输出中的,对在程序的执行过程中各语句的执行对程序输出的影响程度进行估计,并基于这种估计对可疑度的度量方法进行修正.与基于代码覆盖的错误定位技术的对比实验也表明,本文提出的错误定位技术提高或至少维持了错误定位的安全性,并在一定程度上提高了错误定位的精确度.对于工控软件等偶然正确性现象频繁发生的软件,本文提出的错误定位方法可以有效地消除偶然正确性现象带来的副作用所产生的影响.本文根据偶然正确性概率对Tarantula 的可疑度计算方法进行修正,这种方法同样可用于Jaccard 等其他基于代码覆盖的错误定位技术.