内置式减振镗杆减振性能分析

陈林, 李伟, 何全文, 张丽

（四川工商职业技术学院, 四川 都江堰611830）

0 引言

减振镗杆是细长孔加工领域最为理想的工具之一。细长孔是在零件内部进行加工，导致随着孔径深度增加，减振镗杆的悬臂增长。随着减振镗杆加工次数及工作时间增加，镗杆极易出现变形。由于镗杆在镗削过程中，很容易出现振动问题，从而导致加工质量低、表面质量差、加工效率低和刀具磨损严重等问题[1]。因此，研究减振镗杆及提高减振镗杆的刚度是提高深孔镗孔加工精度的重要手段。根据研究分析和技术的应用镗杆减振主要分为3种：一是通过控制系统进行减振；二是通过机器学习进行主动减振；三是通过优化参数进行减振。

参数优化方法因成本较低、可实现性好、稳定性强等优点成为了世界各大刀具制造商的首选方法。早期的研究被动阻尼镗杆的重点是机构镗、阻尼结构、减振器类型、使用新材料和被动阻尼理论。目前国内外学者主要是采用被动阻尼法和主动阻尼法对减振镗杆进行分析。Chen Fan等[2]通过在镗杆上增加磁激励器对镗杆进行主动阻尼的减振。通过仪表控制镗杆振动频率，提高了颤振的稳定性和镗杆的动刚度。哈尔滨理工大学刘强等[3]分析了频率与变质量动力吸振器对减振镗杆性能的影响。通过增加一个可调支架，以增加镗杆的动态刚度。通过将支架固有频率与减振镗杆的自然频率有效结合，可以建立一个新的动态系统并降低新动态系统的振动幅度。此外，通过采用模拟仿真方法对结构和参数进行优化取得了较好的成果。

针对减振镗杆颤振和易变形等问题，本文基于前期的研究分析，建立了减振镗杆的动力学模型，讨论了减振模块不同参量下振幅幅值和振幅频率问题，优化了减振模块的参量，为以后减振镗杆的生产及应用提供了参考。

1 减振镗杆动力学模型

为了分析减振镗杆的减振性能，对内置式可变刚度减振镗杆的动力学及运动学进行了分析。减振镗杆主要由镗杆和可变刚度减振器两部分组成。可变刚度减振器内部主要由阻尼液与减振模块组成，内置式可变减振器安装于镗杆内部。基于动态减振器设计理论，可变刚度减振器放置镗杆前端位置，目的是减少来自阻尼镗杆传递而来的振动。减振模块是可变刚度减振器的关键部件，不仅要确保减振镗杆的刚度问题，同时需保证减振效果及高效吸能问题。根据动力吸振器理论，单位体积下减振模块的密度越大，减振阻尼效果越明显。因此，减振模块在材料选取上通常采用高密度材料以达到减振效果。

镗孔过程中由于减振镗杆具有极高的细长比特性，与径向弯曲和切向弯曲相比，减振镗杆在进给或轴向弯曲时的刚性要大得多。因此，需要镗杆的扭转刚度远远大于它的弯曲刚度。在对镗杆进行力学分析时，需要考虑镗杆弯曲振动的径向和切线方向。根据材料力学分析可知，减振镗杆在切削过程中主要受3个力，分别是轴向力、径向力和切向力。然而，该工具的几何分析表明，与径向力和切向力相比，加工过程中轴向力对零件表面加工质量影响较小，可以忽略不计[4-5]。因此，减振镗杆在切削过程中的受力分析可以简化为只受径向力和切向力影响（如图1（a））。

根据前面分析，镗孔过程可以建模为一个统一的长度为L、横截面积为A、弹性模量为E、密度为r、阻尼为c2的欧拉-伯努利梁，一端夹紧，另一端自由振动，径向振动的力学模型，如图1（b）所示。在此力学模型中，假设切削力与切削的横截面积成正比，在截面面积计算过程中，未考虑插入机头的半径。在计算切削力的径向分量时，只关注刀具切削过程中前一次切削过程引起的表面波动切削深度变化。图1（b）中，减振模块被放置于距离固定夹紧端距离为xa的位置处，c2为阻尼系数，m2为减振模块等效质量质心处质量，镗杆总长度为L，镗孔加工位置处距离固定端的距离为xb。根据假设镗杆的横向位移v（x,t）和减振模块的位移VD可以确定为[6]：

图1 钻孔过程示意图及模型

假设，任意位置处减振镗杆的挠度为

式中：qi（t）为未知时变广义坐标；Φj（x）为无减振装置夹紧梁的正交特征函数。 Φj（x）的表达式为

其中,特征值λj是超越方程的解,表达式为

图2中：m1和m2分别为减振镗杆等效质量质心处质量和减振模块等效质量质心处质量；k1为减振镗杆等效刚度；k2为减振模块等效刚度；c2为阻尼系数；F为外部载荷；x1为等效质量m1的位移响应；x2为等效质量m2的位移响应。对减振镗杆进行受力分析可以得知，外部载荷F不是固定不变的。根据减振镗杆的振动特性分析，对减振镗杆分析过程中，只考虑载荷波动特征，并将载荷当作具有周期性波动的简谐激励力，则可以表示为

图2 减振镗杆动力学模型

式中：Fa为外部载荷的振幅值；ω为外部载荷的角频率。

根据图2，对减振系统内各个质量单元进行分析可以得知质量单元m1和m2的受力方程分别为：

假设梁的动力学可以很好地用1阶振型表示，我们可以将系统简化为以下两个2阶方程。根据减振镗杆系统分析，建立了减振镗杆系统的动力学模型[7-15]：

方程（9）的稳态解可以表示为

减振系统的动力学模型的稳态解可以表示为[8-10]

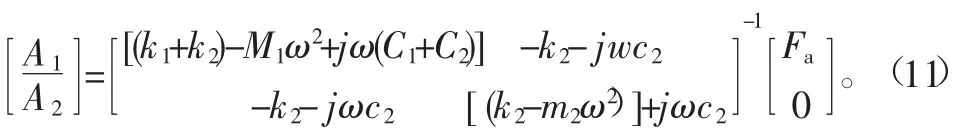
根据减振系统动力学模型，减振模块与减振镗杆的相对振幅为：

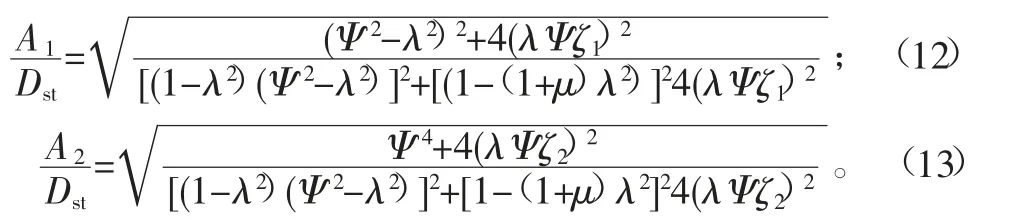
由图3可知，不同阻尼比的所有曲线都经过M、N两点，当频率值低于两点的数值时，减振系统的振幅与系统阻尼无关。这一物理现象是我们设计有阻尼动力减振器的依据，为保证减振器在整个频率范围内都有良好的减振效果,在减振系统选择最佳参数的情况下，振动系统在整个频域内的最大相对振幅为

图3 A1/Dst 与λ的关系

由式（14）可以看出，通过增加减振模块的质量可以降低主系统的振幅，同样减振镗杆的减振效果得到相应提高。因此，需要对减振模块的性能参数进行分析。

3 减振镗杆参量频率分析

影响减振镗杆稳定性的因素很多，根据前期研究和他人的研究结果可知，减振块的密度、阻尼液的阻尼系数和橡胶的支撑刚度对稳定性影响最大。本文对不同参量下的减振镗杆的减振效果进行分析，探究减振镗杆的幅值的时域信息，并分析减振镗杆的频率内谐响应变化曲线。因此本文选取减振器的减振块密度、阻尼系数和支撑刚度进行具体分析。

对减振镗杆进行固态频率分析可知，减振镗杆的4阶固有频率如表1所示，从分析结果可知减振镗杆的1阶和2阶频率都小于1000 Hz，在减振镗杆实际加工过程中，在外部激振频率影响下，减振镗杆很容易在0～1000 Hz范围内出现共振。因此，在分析过程中主要针对减振镗杆的1阶和2阶频率进行分析。

表1 减振镗杆前4阶固有频率 Hz

图4（a）是不同减振块密度下频率在0～1000 Hz范围内减振镗杆的振幅能量变化曲线图，图中K1、K2、K3和K4的减振块密度分别为19 500、20 500、21 500和22 500 kg/m3。从图中可以发现，在0～1000 Hz的激振频率范围中，随着减振块密度的增大，减振频率振幅密度变化曲线不同，减振块密度为22 332 kg/m3时减振镗杆的振幅能量最小，减振效果最好。在1阶频率振幅能量低于2阶频率的振幅能量，造成这种现象的原因是：随着减振块密度增加，减振镗杆的固有频率减小，振幅能量减小。图4（b）是不同阻尼液的阻尼系数下频率在0～1000 Hz 范围内减振镗杆的振幅能量变化曲线图，图中Z1、Z2、Z3、Z4分别代表阻尼系数为0、43、60和100。从图中可以看出，在不同激振频率下振幅能量的变化比较明显，在阻尼系数为43时，减振镗杆的1阶、2阶频率的振幅能量最小。说明当阻尼系数为43时，减振镗杆的振幅最小，减振效果最好。图4（c）是不同橡胶支撑刚度下频率在0～1000Hz范围内减振镗杆的振幅能量变化曲线图，图中M1、M2、M3、M4分别代表支撑刚度为0、3.5×103、7×106、3.5×107N/m2。从图中可以看出，当橡胶的支撑刚度为3.5×103时,减振镗杆在0～1000 Hz的频率内振幅波动相对比较平缓。减振镗杆1阶和2阶频率的振幅随着支撑刚度增大，振幅波动增大。

图4 频率0～1000 Hz不同参量下减振镗杆振幅变化特征

4 减振性能试验验证

通过前面分析可知，减振镗杆的1阶频率主要在300 Hz左右，2阶频率主要在550 Hz左右。在实验分析过程中选取ap=0.6 mm，f=0.35 mm/r，v=25 m/min，刀片选择硬质合金，加工材料选择45钢。对减振镗杆减振性能进行分析，并探究在1阶频率下减振镗杆的振幅曲线。

4.1 减振密度

根据前面公式分析可知，通过提高增加减振器质量和主系统的协同性可以减小减振镗杆的振动幅度，提高镗杆工作的稳定性。在有限的尺寸空间内提高减振器的密度是增加质量的有效途径之一。本文基于前期研究基础对不同密度的减振器进行试验分析，不同减振密度的振幅波动不同。图5（a）为不同减振密度下的减振镗杆振幅时域波动特征，为了更好地分析试验每个减振密度下取1500个数据作为时域特征进行分析。从图5（a）可以发现随着减振密度增大，减振镗杆的振幅降低，波动幅度减小。从图5（b）中可以发现，在不同减振密度下，随着减振器密度的增加，减振镗杆刀尖径向平均振幅降低。说明在减振镗杆内部的有限空间中选取较大减振密度的减振模块可以有效降低减振镗杆的振幅。

图5 阻尼系数对镗杆稳定性的影响

针对1阶频率下不同减振密度下的减振镗杆振幅波动特征，研究了频率在320 Hz 切削力Fa为350 N时不同减振密度下减振镗杆的波动幅值特征，如图6所示。为了更好地反映出系统振幅的变化特征，本文对原数据进行了均处理，以更好地反映出振幅的动态特征。从图中可以看出在频率为320 Hz时，质量密度越大的减振块决定振幅越小。

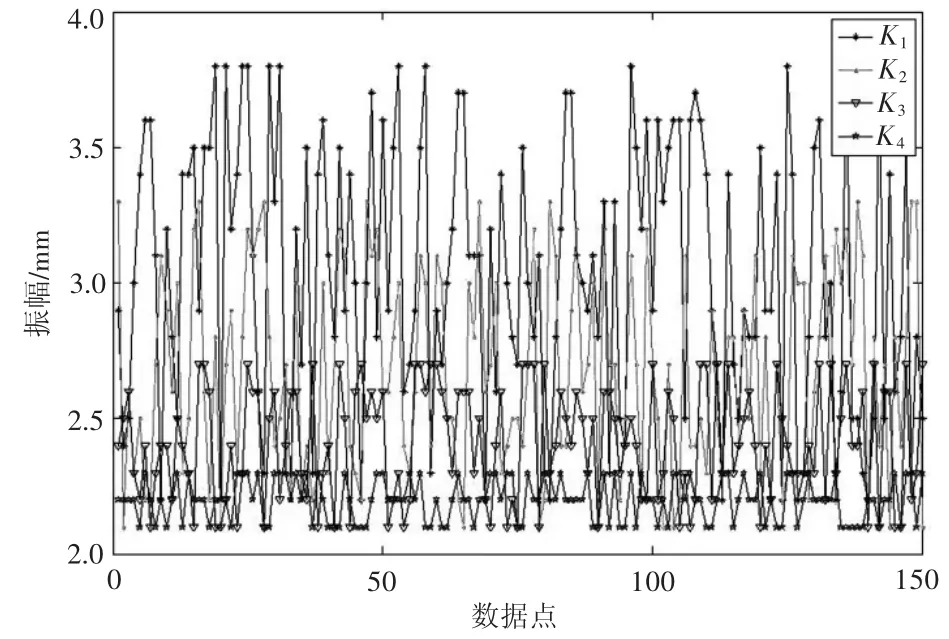
图6 320 Hz时不同质量密度下减振镗杆的振幅动态特征

4.2 阻尼系数

减振模块放置于阻尼液形成一个减振系统并起到稳定作用。因此，阻尼液的阻尼系数是影响减振镗杆振动幅值的另一个重要因素。为了研究阻尼液的阻尼系数对减振镗杆振幅的影响规律，在原来研究基础上，选取4种不同阻尼系数的阻尼液进行分析，如图7（a）所示。从图中可以看出随着阻尼液的阻尼系数增加减振镗杆的振幅波动减小，当阻尼系数为0时，减振镗杆的振幅最大，且波动幅度最大。在阻尼系数为43时减振镗杆的波动幅度最低。从图7（b）中可以看出，随着阻尼液的阻尼系数增加，减振镗杆的振幅呈现为先减小后增加的变化趋势，在阻尼系数为43时，减振镗杆的振幅最小，为3 mm。随着阻尼系数增加，减振镗杆的振幅出现增加，但是增加幅度很小。对4种不同阻尼系数的阻尼液对振幅的频率分析可知，在阻系数为43时，振幅能量较小，这与图6（a）的结论相同。

图7 阻尼系数对镗杆稳定性的影响

图8为在频率为320 Hz时不同阻尼液不同阻尼系数下减振镗杆的振幅值。从图中可以看出阻尼系数对减振镗杆振幅影响较大，与减振块的减振密度相比，采用阻尼液采用合适的阻尼系数可以明显地降低减振镗杆的振幅值。

图7 （续）

图8 320 Hz时不同阻尼系数下减振镗杆的振幅动态特征

4.3 支撑刚度

图9为不同橡胶支撑刚度下的减振镗杆振幅分析。从图中可以看出，发现随着支撑刚度增加，镗杆的振幅呈现先减小后增加的变化趋势，与阻尼系数的变化趋势相似。从图9（a）中可以看出，在不同支撑刚度下，减振镗杆的振幅波动相似，且波动相对较大。当支撑刚度为3.5×106时，减振镗杆的振幅最小，为3.3 mm。对4种不同支撑刚度的频率进行仿真分析，发现，不同支撑刚度下均存在2阶固有频率，且固有频率变化不大。但是在支撑刚度为3.5×106时，频率的振幅能量均相对较小，减振效果最好。

图9 支撑刚度对镗杆稳定性的影响

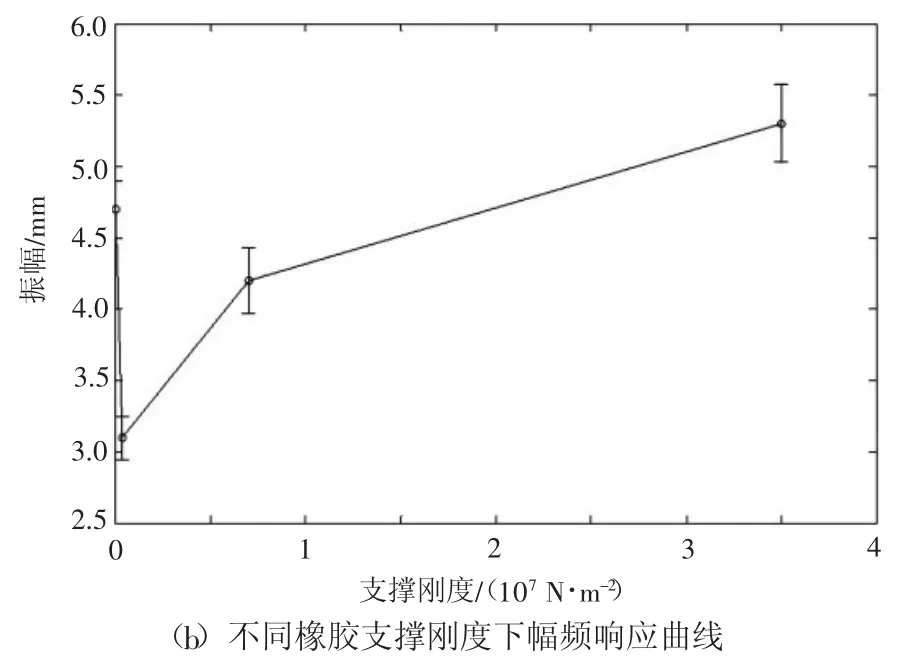
图9 （续）

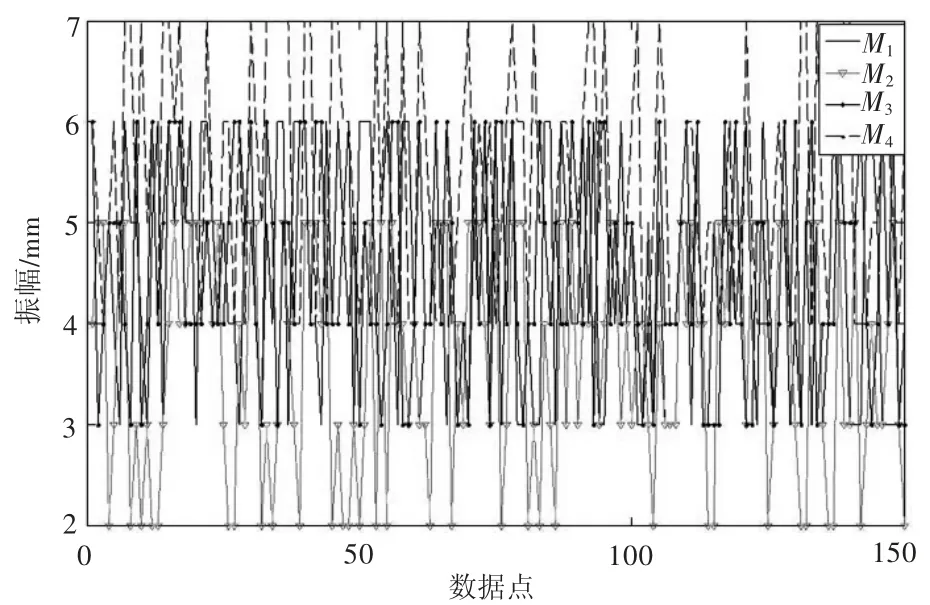
图10 320 Hz时不同支撑刚度下减振镗杆的振幅动态特征

5 结论

本文通过对减振镗杆的结构分析，建立了减振镗杆动力学模型分析。对不同参数下减振镗杆的振幅变化进行了研究。发现镗杆的稳定性和振幅与材料性能存在相关性。镗杆的减振性能随着减振块密度的增大而增强，随着阻尼液阻尼系数和橡胶支撑刚度的增大呈现先增强后减弱的变化趋势。在减振块密度为22 500 kg/m3、阻尼系数43和橡胶支撑刚度3.5×103N/m2时，减振镗杆振幅最小，效果最好。通过动力学仿真曲线对3种参数下的频率响应曲线进行分析，验证了不同参数下减振性能的正确性，为下一步减振镗杆尺寸优化方面进行进一步的分析提供了指导。