基于多因子考虑的地区电网电采暖负荷预测分析

胡志豪，姚锦松，龚立娇，孙开宁，樊 茂，张鹏飞，常喜强，

(1.石河子大学机械电气工程学院，新疆 石河子 832003；2.国网新疆电力有限公司，新疆 乌鲁木齐 830000)

0 引 言

2016年国家能源局发布《关于电能替代的指导意见》，意见指出，在居民采暖领域要逐步推进煤改电工程，促使电能替代燃煤采暖，并根据替代方式的技术经济特点，因地制宜，分类推进[1]。事实上，冬季采用电采暖方式既可以供暖，又可以有效促进新能源的消纳，减少弃风、弃光现象，响应国家政策。同时还可以减少冬季因传统燃煤供暖而造成的空气污染问题，降低雾霾天气出现频率[2]。近年来，电采暖负荷每年以递增的速度接入电网，大规模的电采暖设备向电网注入谐波分量，并在启动过程中造成电压暂降，直接影响电网设备的运行和增加线路损耗等[3-5]。因此，研究电采暖负荷特性，建立有效的预测模型，变得尤为重要。

电采暖负荷受多种因素共同影响，包括经济因素、气象因素、日期类型因素、 随机因素、政治因素、季节因素等。这里主要研究气象因素和日期类型因素。人体舒适度和平均温度是气象因素中重要的衡量指标，可以很好地反映气象条件对电采暖负荷的影响；不同的日期类型，如休息日和工作日也会造成电采暖负荷的波动。

负荷预测有多种方法，如回归分析法、时间序列法、BP神经网络算法、卷积神经网络算法、支持向量机法等。相较于上述算法，最小二乘法(least spuares，LS)拟合简单，理论成熟且通用性强，因此选取最小二乘法拟合作为所提研究的预测方法。

下面研究某地区电采暖负荷特性，利用历史数据，考虑日期类型，分别建立基于平均温度和基于人体舒适度的LS预测模型。实际算例结果表明，这两种方法的预测精度较高，都可以用于地区负荷预测。

1 电采暖负荷模型构建分析

电采暖负荷变化与当地经济发展状况、气象条件、随机事件、节假日等因素有关。基于此，将电采暖负荷增量分为稳定负荷增量、气象敏感负荷增量、随机负荷增量、日期类型负荷增量4个部分[6-7]，即：

(1)

式中：P为电采暖负荷变化量；λs为稳定负荷因子；λw为气象敏感因子；λr为随机负荷因子；λd为日期类型因子。

2 影响因子分析

2.1 稳定负荷因子λs分析

λs为稳定负荷因子，它与当地经济发展水平息息相关，即地区的电采暖负荷特性变动与地区经济、用电结构变动相关[8]。从中短期看，地区经济对电采暖负荷变动影响较小。研究的时间跨度不大，故认为λs对电采暖负荷变化影响权重较小。

2.2 气象敏感因子λw分析

λw为气象敏感因子，此类因子与天气情况、降雨、气温、空气湿度、风速等密切相关。

图1为某地区2019年10月至12月电采暖负荷与气温关系图。总体上电采暖负荷随着时间推移而递增，这与严冬时节来临，气温逐步下降有关。当气温从15 ℃下降到-10 ℃时，电采暖负荷从12 000 MVA上升到约16 000 MVA，负荷增量大。由此可得，λw对电采暖负荷变动影响权重大。

图1 2019年10月至12月电采暖负荷与气温

气象因子对电采暖负荷的影响主要包括室外温度、空气湿度、太阳辐射、风向和风速、降雨(雪)等，其变化规律无法掌握[9]。从单一气象因子看，温度是影响电采暖负荷的最大因素，占60%以上；空气湿度和太阳辐射的影响较小，约占1%～5%[10]。

同时，现在的研究表明，单一气象因子对负荷预测的精度易产生偏差。因此，越来越多的研究普遍考虑综合气象因子对电采暖负荷的影响。综合气象因子由数个单一气象因子耦合而成，主要有实感温度、温湿指数、寒湿指数及人体舒适度等指标[11]。文献[12-13]基于人体舒适度进行负荷预测，预测结果符合预期，反映了人体舒适度和电采暖负荷的高相关性。

人体舒适度是指在不采取任何防寒或防暑措施的条件下，人体在自然环境中的舒适程度[14]，它的计算公式[11]为：

(2)

式中：SD为人体舒适度指数；T为环境温度，℃；Rh为相对湿度，%；v为风速，m/s。

综上，选取平均温度、人体舒适度两个指标来预测负荷。

2.3 随机负荷因子λr分析

λr为随机负荷因子，往往由突发事件引起。由于突发事件不可预测，无法用公式衡量，同时它对整个负荷变动贡献相对较小，因此认为λr=0[15]。

2.4 日期类型因子λd分析

λd为日期类型因子，它与负荷一样具有周周期性。负荷的周周期性是指一周7天负荷变化所体现的规律[16]。一般情况下，星期六、星期日属于休息日，电采暖负荷较轻；而星期一至星期五为工作日，人们需要进行生产活动，电采暖负荷较高[17-18]。

图2为某地区电采暖负荷星期一至星期日电采暖平均负荷趋势图。数据采集时间为2019年10月11日至2019年12月26日，共计77天，11周。研究图2可得，工作日的日均负荷为14 499 MVA，休息日的日均负荷为14 361 MVA，前者比后者多138 MVA。可知λd对电采暖负荷变动影响权重较大。

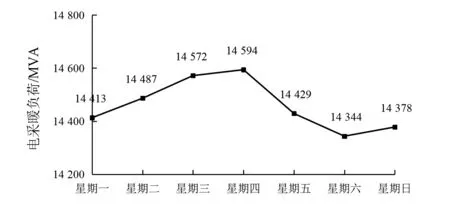
图2 星期一至星期日电采暖平均负荷变化

综上分析，在中短期内，日期类型因子λd、气象敏感因子λw会显著影响电采暖负荷变化，而随机负荷因子λr、稳定负荷因子λs对负荷变化影响较小。因此，电采暖负荷预测主要考虑λw和λd这两个因素。

3 负荷预测模型构建

3.1 样本数据预处理

通常情况下，负荷预测是基于历史数据的。但是由于传感器精度等原因导致负荷预测所采用的历史数据不一定准确。与此同时，突发事件也会影响负荷的大小[19]。为避免预测结果的偏差，将对异常数据进行处理，选取其前2日及后2日负荷平均值作为新数据：

xn=(xn-2+xn-1+xn+1+xn+2)/4

(3)

式中：xn为异常电采暖负荷；xn-2、xn-1、xn+1、xn+2分别为异常负荷前2日、前1日、后1日、后2日的电采暖负荷数据。

3.2 预测模型方法

采用最小二乘法对电采暖数据进行线性拟合。最小二乘法是一种数学优化建模方法。它运用逼近原则寻求数据，让实测数据与估计数据平方和最小，即距离和最小，来寻测和匹配最佳的函数数据，从而拟合函数曲线[20]。

最小二乘法是由勒让德在19世纪发现的，形式为

目标函数=∑(观测值-理论值)2

(4)

观测值为数据样本，理论值就是所假定的拟合函数。目标函数即是机器学习中的损失函数，最终目的是得到使目标函数最小化时的拟合函数的模型。样本hθ(x)为n次的多项式拟合，公式为

hθ(x)=θ0+θ1x+θ2x2+θ3x3+…+θnxn

(5)

式中，θ0、θ1、θ2、θn为参数。最小二乘法就是求：

(6)

式中，yi为电采暖实际负荷。

3.3 预测模型的建立

采用最小二乘法线性拟合进行负荷预测流程具体如下：

1)对输入的历史负荷数据进行预处理，选取N组样本数据，对异常数据平均化处理。

2)区分日期类型，分别选取平均温度和人体舒适度两个指标，对电采暖负荷数据采用最小二乘法线性拟合获得预测模型。

3)进行负荷预测，并将实际负荷与预测负荷进行误差比较。平均绝对百分比误差(MAPE)是一种衡量预测误差的一个指标，其计算公式为[20]

(7)

式中：Emap为平均绝对百分比误差；Pi为第i个实际电采暖负荷值；Pi′为第i个预测点的电采暖负荷值。

4 实际算例

所使用的每日电采暖负荷数据集来自某电力公司，气象数据集来自于天气网站http://www.meteomanz.com，其包含以下气象因素：日最高温度、日最低温度、日平均温度、每日风向及平均风速、每日平均相对湿度等。

样本数据选取某地区2019年10月11日至2019年12月10日共计61日的电采暖负荷及天气数据。区分日期类型，分别采取平均温度和人体舒适度两个指标与电采暖负荷线性拟合建模。

4.1 基于平均温度分析

考虑日期类型，将电采暖负荷数据与平均温度线性拟合，分别得到两者之间的拟合关系，如图3、图4所示。式(8)、式(9)分别为基于平均温度的工作日电采暖负荷预测模型和基于平均温度的休息日电采暖负荷预测模型。

P1=-173Tav+14 472

(8)

P2=-162Tav+14 246

(9)

式中：Tav为平均温度，℃；P1、P2分别为基于平均温度的工作日和休息日的电采暖预测负荷，MVA。

图3 基于平均温度的工作日电采暖负荷预测

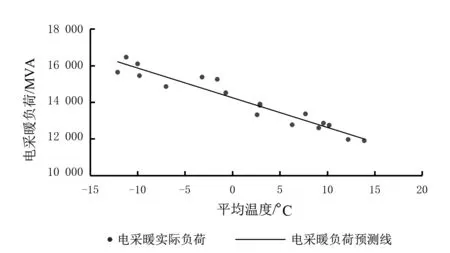
图4 基于平均温度的休息日电采暖负荷预测

4.2 基于人体舒适度分析

考虑日期类型，将电采暖负荷数据与人体舒适度线性拟合，分别得到两者之间的拟合关系，如图5、图6所示。式(10)、式(11)分别为基于人体舒适度的工作日电采暖负荷预测模型和基于人体舒适度的休息日电采暖负荷预测模型。

P3=-98SD+17 216

(10)

P4=-90SD+16 754

(11)

式中：SD为人体舒适度指数；P3、P4分别为基于人体舒适度的工作日和休息日的电采暖预测负荷，MVA。

图5 基于人体舒适度的工作日电采暖负荷预测

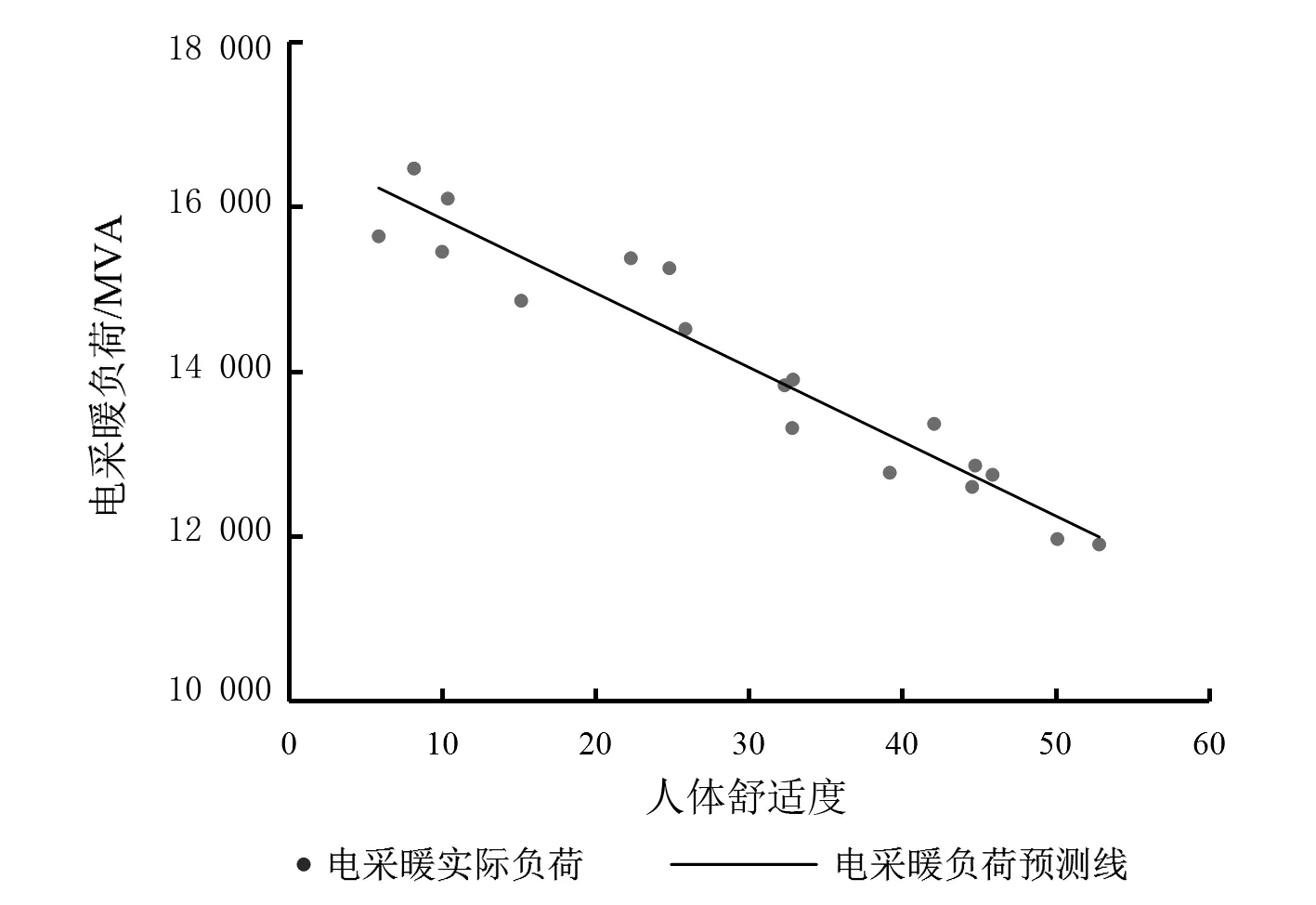
图6 基于人体舒适度的休息日电采暖负荷预测

图3至图6描述了平均温度、人体舒适度与电采暖实际负荷的关系。随着平均气温、人体舒适度提高，电采暖负荷总体上呈下降趋势，下降趋势可近似看作一条直线。图3至图6中的直线是依据模型建立的电采暖负荷预测线，可用于负荷预测。

4.3 预测结果

表1为2019年12月11日至2019年12月29日负荷预测结果。表2为两种预测方法的MAPE，两种预测模型的MAPE相近，且都小于2 %，达到了良好的预测效果。

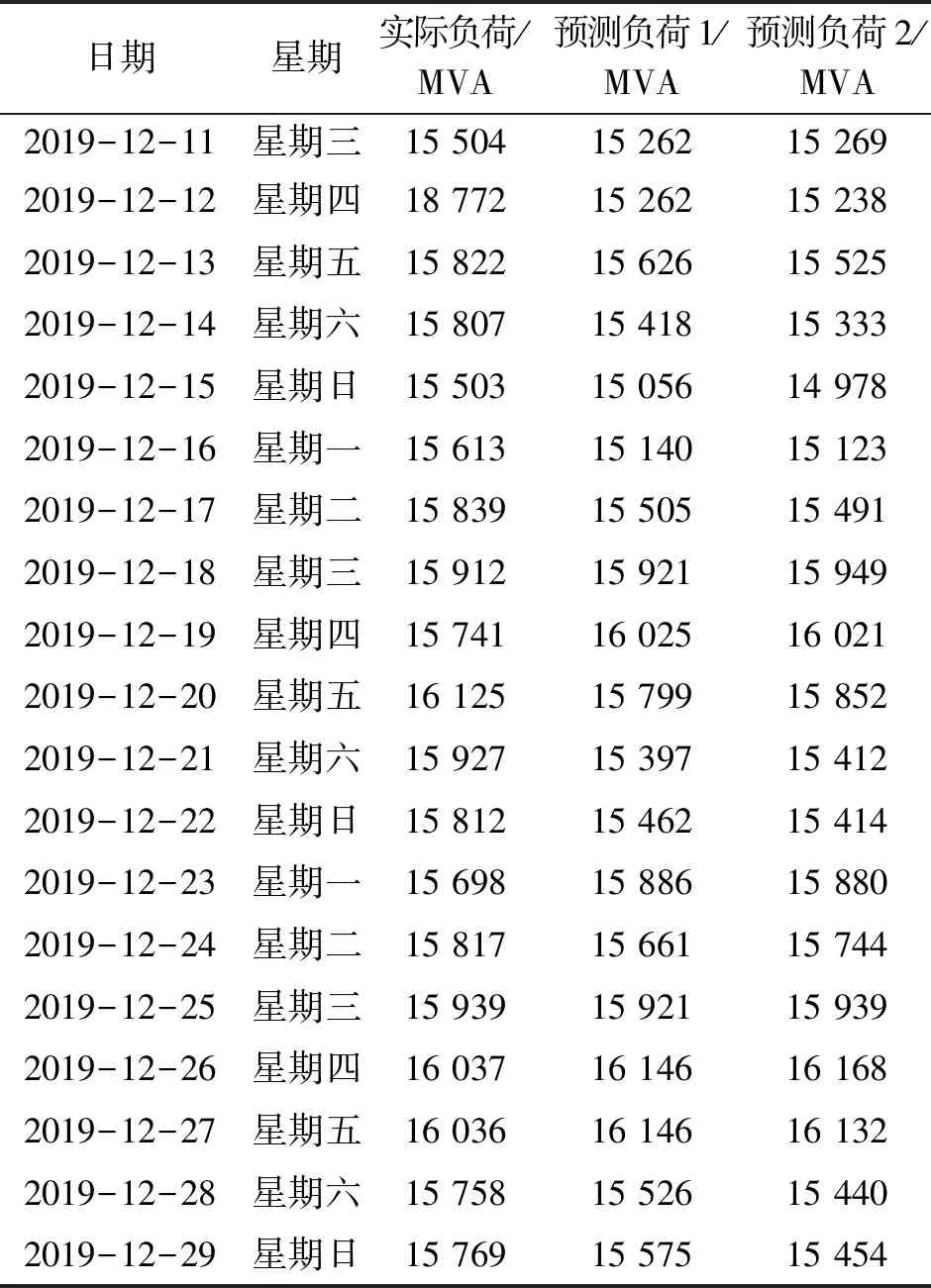
表1 电采暖负荷预测结果

表2 负荷预测平均绝对百分比误差

5 结 语

前面对影响电采暖负荷变化的多个因子进行分析发现，日期类型因子λd、气象敏感因子λw会显著影响电采暖负荷变化，而随机负荷因子λr、稳定负荷因子λs对负荷变化影响较小。

因此，建立了考虑日期类型的基于平均温度的LS预测模型和考虑日期类型的基于人体舒适度的LS预测模型。由预测结果知，所提出的两种预测模型都能够准确反映实际负荷的变化趋势，精度较高，可应用于地区电采暖负荷预测。