单相LCL型并网逆变器陷波器阻尼与无源控制策略

谢建林，张 鑫，陈婷婷，周 浩

（湖北工业大学，湖北 武汉 430000）

0 引 言

并网逆变器作为分布式电源的重要组成部分成为了人们讨论的焦点。当逆变器工作在理想电网的情况下，入网电流产生的谐波分量对电网的影响几乎可以忽略不计。但由于实际远距离的输配电线路给电网引入了大量的线路阻抗，逆变器并网电流流过阻抗产生的谐波电压会使电网电压产生畸变[1]。并且为了改善逆变器的输出波形，对比分析了L型滤波器、LC型滤波器以及LCL型滤波器的特点，发现LCL型滤波器更加适用于并网逆变器。然而LCL滤波器在谐振频率处存在一个谐振尖峰，如果不对谐振尖峰进行抑制，那么系统将会对电网产生很大的不良影响。

通常谐振问题是由于逆变器系统阻尼不够造成的，因此需要通过增加系统阻尼来解决此问题。目前，增加系统阻尼的方式包括无源阻尼法和有源阻尼法两种。无源阻尼法在电容支路串联的电阻会增加系统额外功耗，从而降低系统效率，有源阻尼法通过算法来增加系统阻尼，所以不会有额外功耗。比较常用的有源阻尼法有系统前向回路中串联陷波器控制和基于电容电流比例反馈控制等方法[2,3]。上述方法虽然都可以解决系统阻尼问题，但不可避免的需要增加传感器，致使系统的成本提高。另外对于电网电流的控制策略分为线性控制和非线性控制，其中线性控制包括比例积分（Proportional Integral，PI）控制、比例谐振（Proportion Resonant，PR）控制、重复控制以及预测控制等，非线性控制包括滞环控制、滑模控制（Sliding Mode Control，SMC）以及神经网络等[4-10]。上述方法从基于经典控制理论传递函数的角度来分析问题，有着鲁棒性不佳等缺陷。近年来无源控制策略因其从系统能量的角度出发，使系统的鲁棒性得到提高而被广泛地应用到光伏系统中[11-13]。

本文在现有研究基础上完成了LCL型并网逆变器的EL数学模型搭建，然后采用陷波器的阻尼方式设计了无源控制器，验证了系统在期望平衡点处的稳定性。并且在MATLAB/Simulink中搭建了LCL型并网逆变器EL数学模型分析仿真波形，通过分析仿真波形验证了系统的可行性。

1 单相LCL型并网逆变器的数学模型

三相LCL型并网逆变器的拓扑图如图1所示。其中Udc为直流侧电压源，S1～S4为4个IGBT开关管，L1和L2分别为逆变侧和电网侧的电感，R1和R2分别为逆变侧和电网侧的电阻，C为滤波电容。因实际中分布式电源和电网存在一定输送距离，其中线路的等效电阻和电感分别用Rg和Lg代替。i2为逆变侧电流，Uc为滤波电容两端电压，ic为流过滤波电容的电流；i2为电网侧电流，Ue为电网侧电压。

图1 三相LCL型逆变器拓扑图

选取控制系统变量电容电压Uc、逆变器输出电流i1以及并网电流i2。考虑滤波电容上电阻Rc时可以得到系统的状态方程为：

式中，Uab为逆变器ab两点输出电压，整理可以得到系统并网的动态方程为：

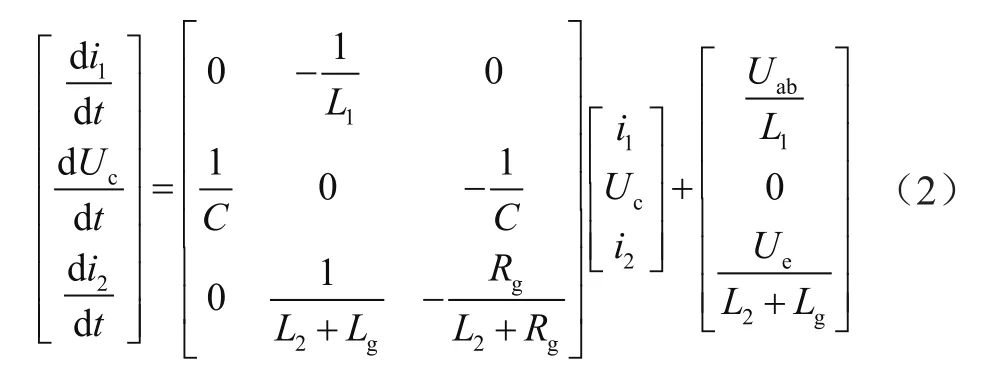
可以写成EL模型的形式为：

式中，M为正定的对角矩阵；J为反对称矩阵，J=-JT，反映了系统内部的互联结构；R为对称正定矩阵，反映了系统的耗散性；u则表示为系统与外界的能量交换。即

2 LCL型并网逆变器无源控制器设计

2.1 系统无源性

如果存在一个连续可微半正定函数H(x)（储存函数），使得：

成立，则系统是无源的。

式（4）也可以写为：

对于逆变器系统而言，如若存在半正定能量存储函数H(x)和正定函数Q(x)，对∀T＞0使得：

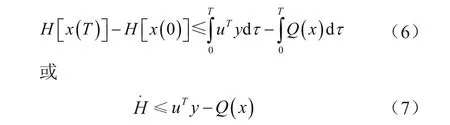
对系统的输入u，输出y及能量供给率uTy成立，则该系统为严格无源系统。

令y=u、Q(x)=xTℜx，代入式（8）后与式（6）相对比可发现形式相同，则LCL型逆变器系统为严格无源的。并可进行无源控制器的设计。

2.2 控制器设计

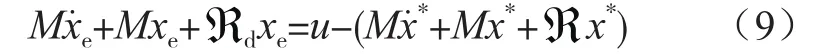
式（9）中x*为系统的期望平衡点。为了让系统更快的收敛于期望平衡点，可以为系统注入阻尼，加快系统能量的耗散。设阻尼耗散项为：

为控制并网电流i2，则令并根据系统的无源控制率可以得到单相LCL型并网逆器

的结构框图和无源控制框图如图2，图3所示。

图2 LCL型逆变器无源控制

图3 LCL型逆变器结构框图

3 仿真实验分析

LCL型滤波器会产生一定的谐振尖峰，进而对输入电网电流的质量产生很大影响。从文献[11]可得知，简单的无源控制器虽然可以满足电网低次谐波要求，但在高频段没有对谐振尖峰起到很好的抑制作用，所以需要在无源控制器的基础上通过增加合适阻尼方法，来有效抑制LCL滤波器产生的谐波尖峰，从而优化逆变器的性能。

无源阻尼法相对较简单，不需要额外的传感器，只需要在LCL滤波器的支路中串联或并联电容。文献[12]指出由于该方法只适用于低频段，并会额外增加系统的损耗，所以在实际工程中并不适宜。有源阻尼法本质都是通过算法来增加系统的阻尼，从而达到抑制谐波尖峰的目的，但由于电容电流比例反馈和一些其他有源阻尼方式都需要增加传感器，导致系统成本上升。因此，经过对比，在不额外增加传感器的情况下，利用陷波器的陷波特性也能对高频段谐波起到很好的抑制效果。

为了验证陷波器阻尼法的有效性，先对陷波器的特性进行分析。陷波器的传递函数为：

式中，ξ为陷波器的阻尼系数；ωn为陷波器反向谐振角频率。从式（14）可得知陷波器会在频率为ωn处产生一个反向尖峰，而在其他处的增益为0，因此通常选用LCL滤波器的谐振频率点设为ωn的值。下面将分析各参数对陷波器幅频特性的影响。陷波器参数Bode图如图4所示。

从图4中可以看出，若ωn的值选取为LCL滤波器的谐振频率点，那么陷波器在ωn处产生的反向谐振尖峰可以抵消LCL型滤波器在谐振点处的正向尖峰，从而达到阻尼的效果。阻尼系数ξ会影响陷波器抑制尖峰的范围，ξ越小，抑制尖峰的范围越窄。

图4 陷波器参数Bode图

下面将继续从Bode图的角度分析将陷波器加入到LCL型并网逆变器系统中的可行性。在理想电网的情况下，即线路电阻R1=0 Ω；R2=0 Ω电网阻抗不考虑Lg=0 mH=；Rg=0 Ω。选取逆变侧电感L1为3 mH，逆变侧电感L2为0.8 mH，滤波电容C为20 μF。则可以算出系统的谐振频率为：

从上述可知，让ωr1=ωn时，可以实现对LCL滤波器产生谐波尖峰的抑制。选取阻尼系统ξ为0.7，陷波器的传递函数变为：

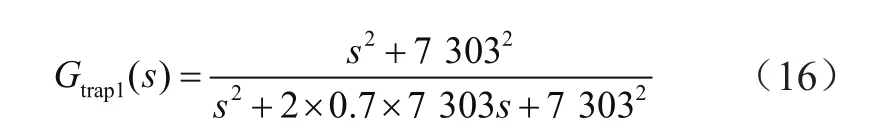
得到理想电网下LCL滤波器加入陷波器后的伯德图仿真如图5所示。

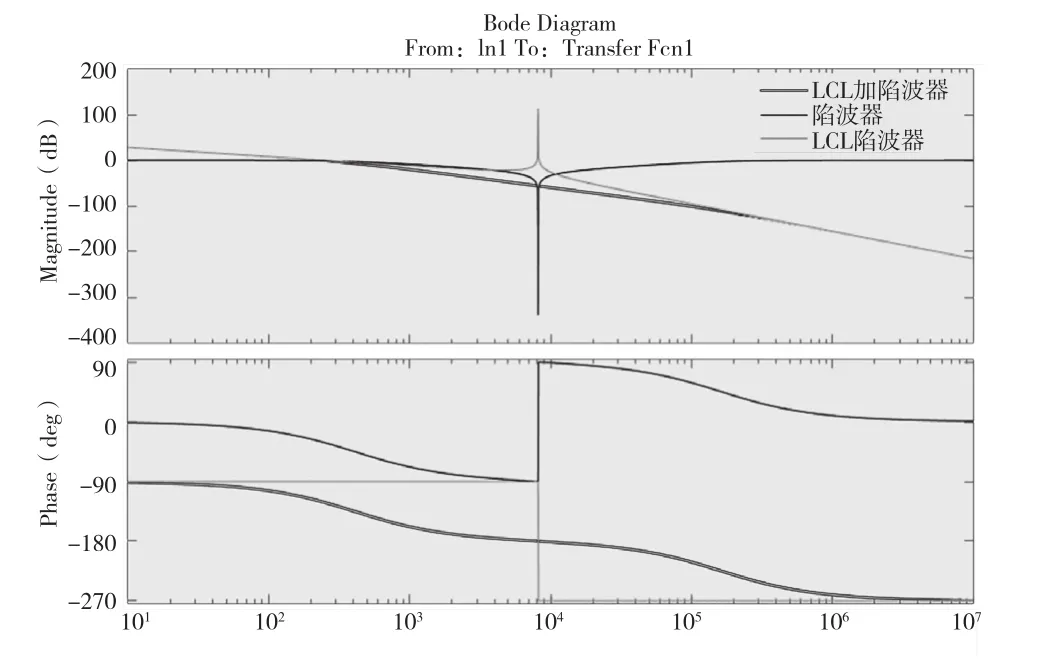
图5 理想电网下LCL型滤波器与陷波器伯德图

图5中红线代表陷波器Gtrap1(s)的伯德图，黄线代表LCL滤波器的伯德图，蓝线代表加入陷波器Gtrap1(s)后的LCL滤波器伯德图。从图5中的红线不难看出系统在谐振频率附近的增益降低到了0 dB一下，谐波尖峰得到了有效的抑制。

上述分析结论只能用于理想电网的情况下。同理，将分析系统在弱电网中的可行性。取电网阻抗Rg为0.05 Ω，电网感抗Lg为0.2 mH。通过计算得出系统的谐振频率为ωr2≈6 473 rad/s，则陷波器的传递函数变为：

得到系统的伯德图如图6所示。

图6 弱电网下加入陷波器后系统伯德图

从图6中可以得出，加入陷波器阻尼后在弱电网下系统的谐振尖峰得到了很好的抑制。下面将陷波器串联到无源控制器后对系统进行仿真分析。

图7 加入陷波器后系统控制框图

LCL型逆变器的结构框图变为：

取直流侧电压Udc为650 V，选取电网阻抗Rg为0.05 Ω，电网感抗Lg为0.2 mH，频率为50 Hz。额定输出相电流峰值为50 A，半载时输出相电流峰值为20.51 A，额定输入电流为55 A，额定功率为35 kW。陷波器阻尼系数Ka=100。根据图8在MATLAB/Simulink中搭建了仿真模型，仿真波形如图9所示。

图8 加入陷波器后的系统结构框图

图9 加入陷波器后系统的动态响应曲线

其中图9（a）为并网电流波形，在系统运行0.1s时并网电流i2从90 A突变到45 A进行半载实验，经过0.2 s的半载实验后并网电流从45 A恢复到90 A。虽然进入半载时系统需要一定时间达到稳定，但整体波形还是比较平稳。图（b）为并网有功与并网无功功率，从中可以看出系统稳定后的输出比较稳定。图（c）为并网功率因数，可知不管是工作在额定负载还是工作在半载并网功率因数都在0.9以上。图（d）为并网电流THD，并网电流THD输出基频值为89.69 A，THD为0.77%，系统整体输出波形良好。

陷波器有源阻尼与无源控制器下，并网电流谐波含有率的IEEE 1547标准要求与仿真结果如表1所示。

表1 并网电流谐波含有率

从表1的陷波器有源阻尼与无源控制器的仿真谐波含有率可得，系统输出的并网电流可以满足IEEE 1547标准要求。加入陷波器后的LCL型并网逆变器在谐振频率点处对谐振尖峰的抑制效果明显，输出波形良好，并且减少了系统传感器的数量，降低了系统成本，验证了控制方法的可行性。

4 结 论

通过对LCL型并网逆变器的数学模型进行分析，建立了基于EL的系统数学模型，并进行了无源控制器的设计。但系统用简单的无源控制器输出的高频段波形并不理想，所以为了优化系统并入电网的波形，提出了加入合适阻尼的方式。为了降低系统成本，本文决定选取陷波器有源阻尼法。加入陷波器后的LCL型并网逆变器系统输出波形稳定，满足IEEE 1547标准要求。

对于实际工程中，弱电网的阻抗感抗有可能会随时发生变化，就会导致系统的谐振频率出现偏差，导致输出波形的不理想，文献[14]提出的一种自适应陷波器法可以实时的计算系统的谐振频率从而增加系统鲁棒性，如何将该类型方法改进融入到本课题中是今后研究的方向。