深圳地铁9号线下穿某河道“门”式抗浮结构计算方法探讨

卢 斌，王国建

(1.中建水务环保有限公司,北京 100071；2.深圳市水务规划设计院有限公司，广东 深圳 518000)

中国城市化的快速发展使得城市交通需求越来越大，地铁以其节省城市有限土地资源，载客量大，通勤时间短，污染小等优点，在一线和省会城市备受青睐，目前全国已有39座城市拥有地铁[1]。河流水系是城市重要的排水通道，为区域高程低点，导致部分地铁隧洞穿越城市河流段覆土较薄，近年来其抗浮设计、施工方案相关研究越来越多。“门”式抗浮桩阀结构形式简单，抗浮效果明显，已有多个案例采用此结构辅助地铁隧道抗浮[2-7]。由于地铁盾构隧道、抗浮结构、河道关系复杂多变，施工时序影响因素较多，较多论述采用定性分析和探讨施工要点，较少对结构计算方法进行探讨。

本文以深圳市前海片区某河道与深圳地铁9号线地铁隧洞“门”式桩阀抗浮结构为研究对象，将复杂结构简化为简单力学模型，采用结构力学法定量分析结构内力和位移变形，并通过有限元数值方法分析验算。

1 工程概况

深圳某河道位于前海合作区，主槽宽度20 m，主槽底高程为-1.62～-1.64 m，与外海连通。该河道与地铁9号线基本正交，地铁9号线隧洞顶高程为-3.5 m，距现状河底仅1.87 m。根据勘察成果，河道与地铁交叉段场地高程5.00～5.96 m，自上而下分别为素填土层、填石层、淤泥层、砂质黏土、残积土、全风化混合花岗岩。河道主槽高程位于砂质黏土层，地铁隧洞位于残积土层(图1)。地下水位具有连续性，水面较稳定，枯季地下水位高程在2～4 m范围内，受潮汐影响小，主要受降雨影响。

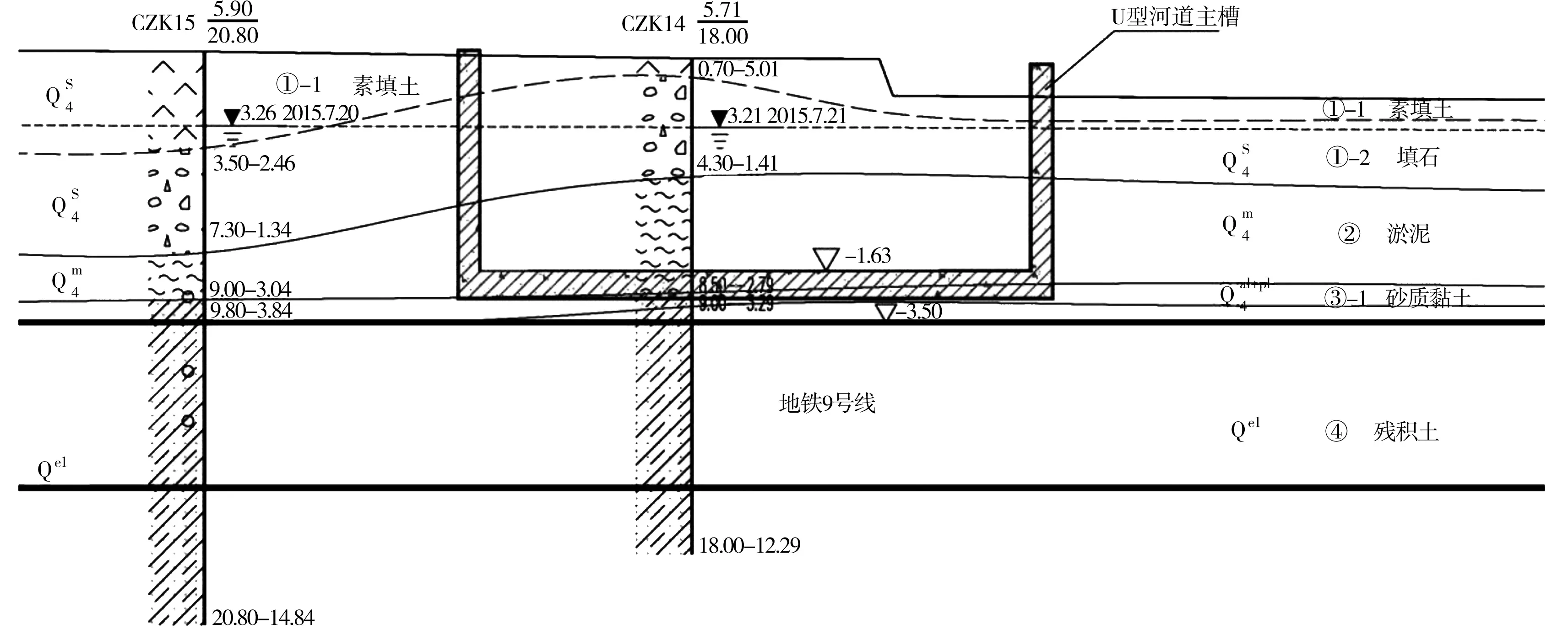
图1 河道与地铁交叉高程关系及地质剖面

2 河道与地铁隧道交叉段设计方案

由于河道水动力条件相对较差，需定期清淤，为保障清淤不影响下部地铁结构采用U型槽河道结构。考虑清淤恰发生降雨为最不利工况，此时U型河道主槽+地铁隧道上浮力叠加。根据GB 50157—2013《地铁设计规范》，不计入侧壁摩阻力，抗浮安全系数要求不低于1.05；计入侧壁摩阻力，根据不同地区的水质和水文地质条件，抗浮安全系数可采用1.10～1.15[14]。经验算，此时U型槽结构抗浮系数Kf仅为0.55，不满足抗浮需要，需增加辅助抗浮结构。不考虑侧壁摩阻力，结构整体抗拔力按式(1)：

Fk=1.05G-Ff

(1)

式中G——结构重力；Ff——结构浮力。

为保障地铁9号线施工期和运营期安全，河道与地铁9号线交叉河段设置“门”式抗拔桩+阀板结构辅助抗浮。根据JGJ 94—2008《建筑桩基技术规范》，单桩抗拔力按式(2)[15]：

Tua=∑λiqsiauili

(2)

式中ui——桩身周长；λi——抗拔系数；qsia——桩间第i层土侧阻力标准值；li——桩间第i层土的厚度，m。

根据地铁保护范围和地铁抗浮计算要求，“门”式抗拔桩+阀板结构顺水流方向长39.0 m，垂直河流方向宽21.6 m，河道堤防结构采用U型槽结构，抗浮筏板厚1.0 m，抗拔桩布置3排24根(两侧各7根、中部10根)，桩径1.2 m，桩长20 m，设计方案见图2。

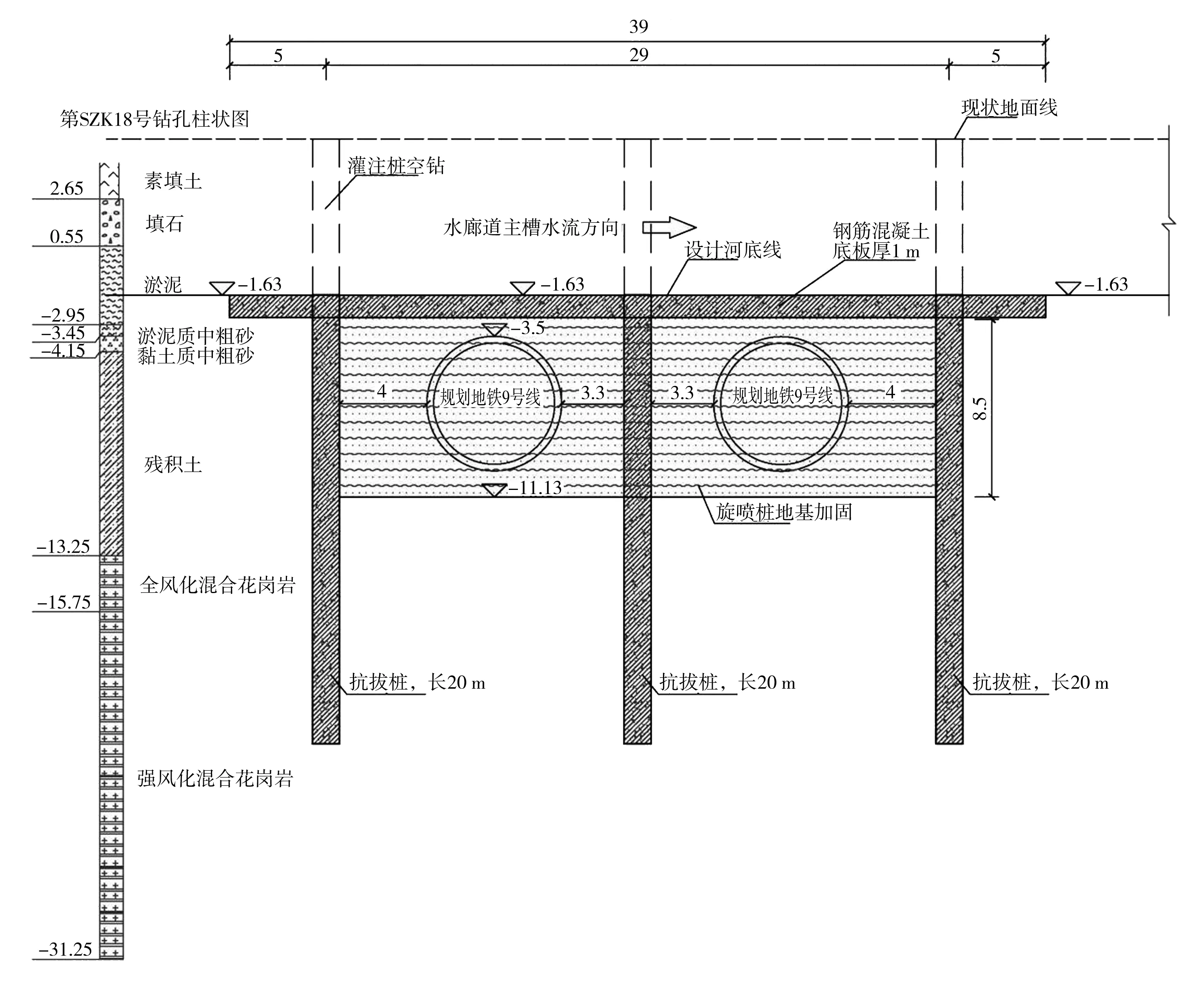
图2 某河道地铁交叉段“门”式桩阀抗浮结构设计方案(m)

3 “门”式桩阀抗浮结构内力和位移计算

3.1 结构力学方法计算

a)结构受力简化。在河道清淤维护期间，河道主槽无水，地铁隧洞区间无车辆运行，U型主槽+地铁隧道上浮力叠加，对计算模型进行简化：①不考虑土体对隧洞外壁、U型槽侧壁的黏聚力和摩阻力；②盾构隧洞上部和抗浮板底面之间存在0.9 m土体，上浮力在此土层中产生一定应力扩散，扩散角按照《建筑地基基础设计规范》计算取18°[15]；③抗拔桩支座刚度较大，计算时按照弹性支座考虑；④顺水流方向为双向板短跨方向，取顺水流方向单位宽度结构进行计算，相应浮力荷载均转换为每延米荷载进行计算。经计算U型槽受浮力q1=66.30 kN/m(考虑1.05抗浮系数)，U型槽自重和覆土荷载q2=46.08 kN/m；地铁9号线隧洞上浮荷载q3=49.46 kN/m。抗拔桩限制筏板竖向变形，抗拔桩与筏板结合处视为弹性支座，两端为自由端，“门”式桩阀抗浮结构计算简化为4跨连续梁结构，单位宽度上梁断面尺寸B×H=1.0 m×1.0 m，见图3。

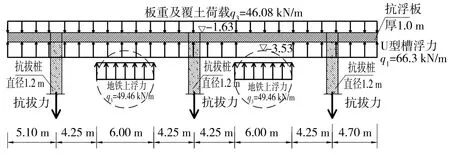
图3 抗浮工况“门”式桩阀结构受力简图

b)结构内力和位移。通过结构力学超静定结构多节点连续梁力矩分配法[16]进行求解简化的“门”式桩阀抗浮结构梁内力。根据《混凝土结构设计规范》连续梁对支座弯矩适度调幅[13]，得到弯矩图、剪力图和位移图，见图4。计算结果表明，结构两端为自由端，弯矩为0，最大负弯矩位于板中支座处-1 027.19 kN·m；在第一跨和第二跨板中，受地铁隧道上浮力作用，弯矩较大，分别为1 016.19、1 031.89 kN·m。作为支座的抗拔桩两侧剪力相反，剪力最大值位于板中支座两侧，分别388.64、-378.41 kN；板两端为自由端，剪力值为0。抗浮筏板受整体浮力和地铁上浮力影响，第二跨和第三跨板中位移分别为3.45、3.57 mm；抗浮筏板两端受整体受力影响，产生向下变形位移。

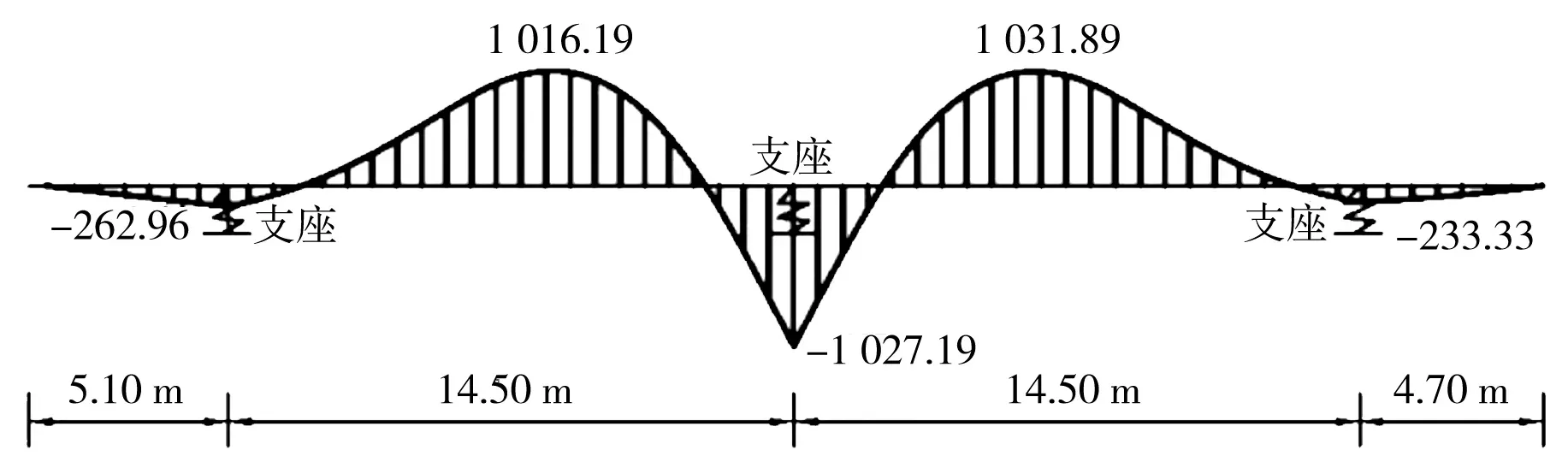
a)弯矩(单位：kN·m)

3.2 有限元方法分析验算

a)有限元计算模型。根据结构尺寸和地质勘察成果资料建立“门”式桩阀抗浮结构二维有限元数值模型，验算相同工况下结构内力和位移(图5)。二维有限元模型长39.0 m、高24.5 m，划分为6种材料，8种单元(其中抗拔桩与土体接触面设置主动、被动接触2个单元)。模型底部边界为强风化混合花岗岩，设置竖向约束固定，两侧边界设置水平约束固定，二维模型共划分1 784个单元，1 832个节点。

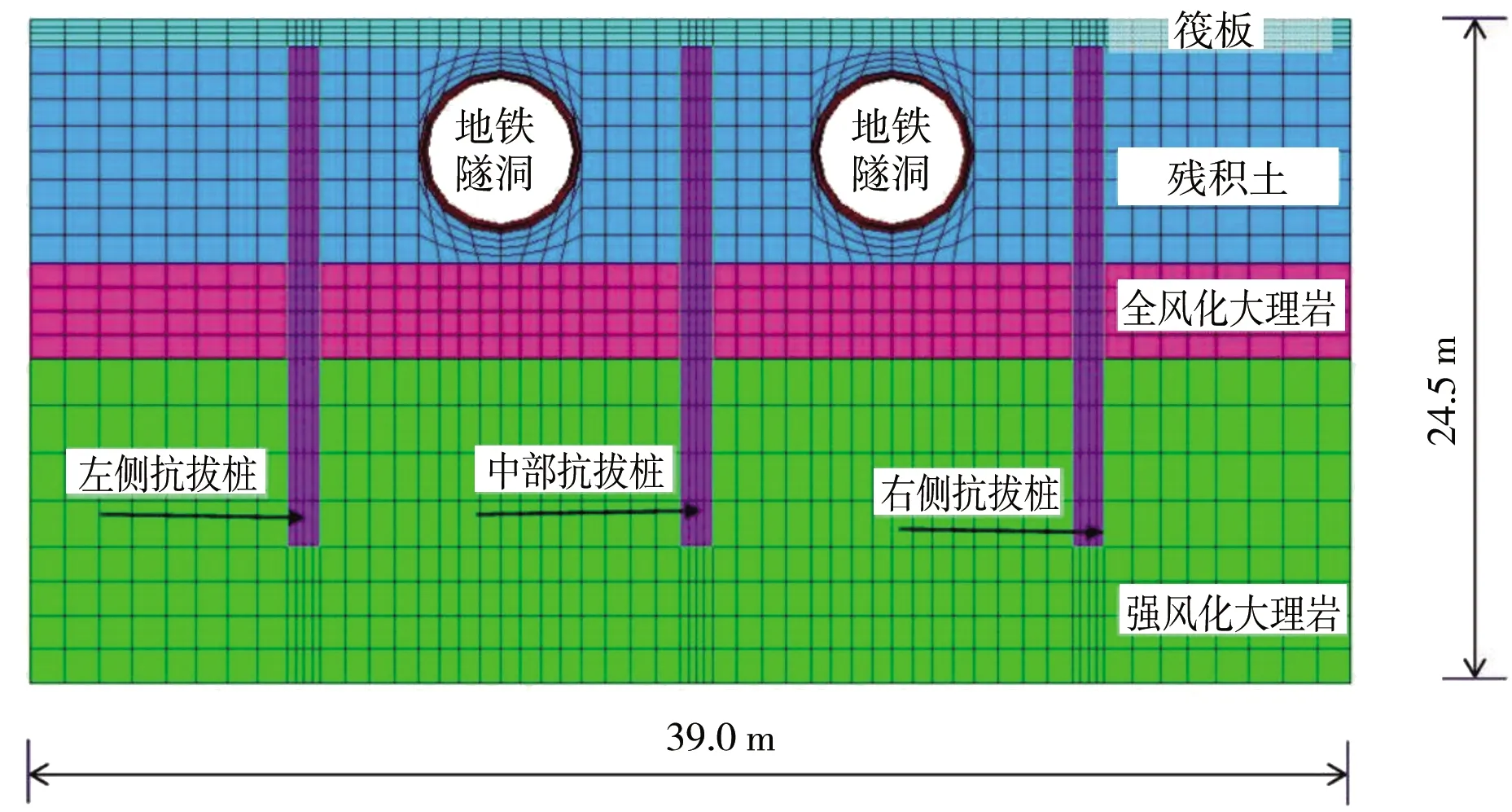
图5 数值分析计算有限元模型

b)有限元计算结构内力和位移。根据图6计算结果，“门”式桩阀抗浮结构在自重和浮力荷载作用下，位于盾构隧道抗浮筏板上部结构上部受拉，下部受压，拉应力最大为1.02 MPa，压应力最大为-0.96 MPa。抗拔桩与筏板交接处受拉，拉应力值为0.80 MPa，桩端抗浮板上部为受压，压应力-0.85 MPa。抗拔桩两侧剪应力方向相反，抗拔桩与筏板交界处剪应力最大，其中中部抗拔桩剪应力最大值为104.15 kN，最小值为-105.11 kN。抗浮筏板两端位移为0，地铁隧道上部筏板位移最大，为2.65 mm。

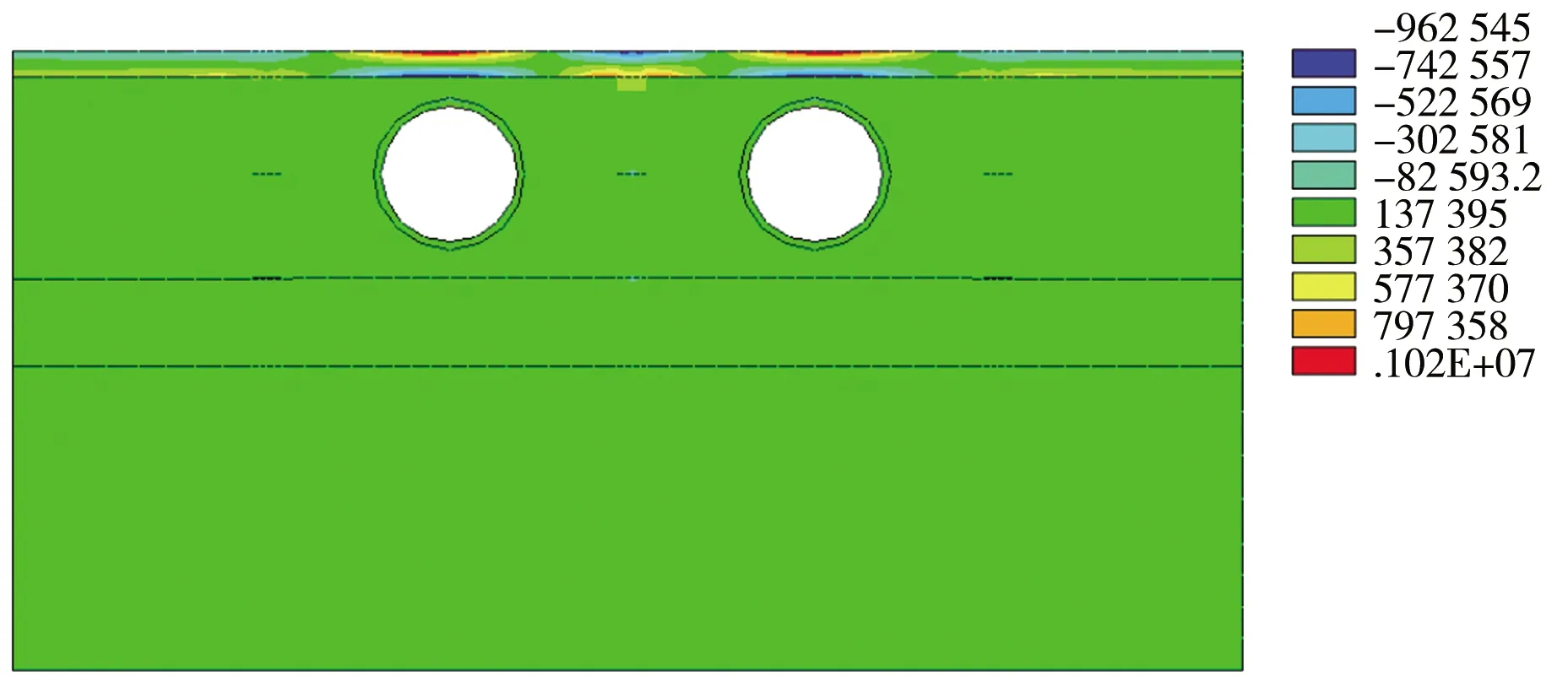
a)X方向应力云图(单位：Pa)

有限元分析计算结果为节点应力，剪力需通过节点剪应力叠加求和，弯矩需根据X方向应力对对应截面求矩。提取相应截面应力并进行相关计算求解截面内力得到图7，结果表明，抗浮筏板结构两端为自由端，弯矩为0，弯矩最大值分别位于地铁隧道上部抗浮筏板跨中，左跨最大弯矩为1 165.28 kN·m，右跨为1 162.41 kN·m，板中支座处-1 029.65 kN·m；抗浮筏板两端为自由端，剪力值为0，支座两侧剪力相反，剪力最大值出现在板中支座左右两侧，分别为190.91、-190.83 kN。抗浮筏板受整体浮力和地铁上浮力影响，第二跨和第三跨板中位移为2.65 mm，两侧自由端位移为0。

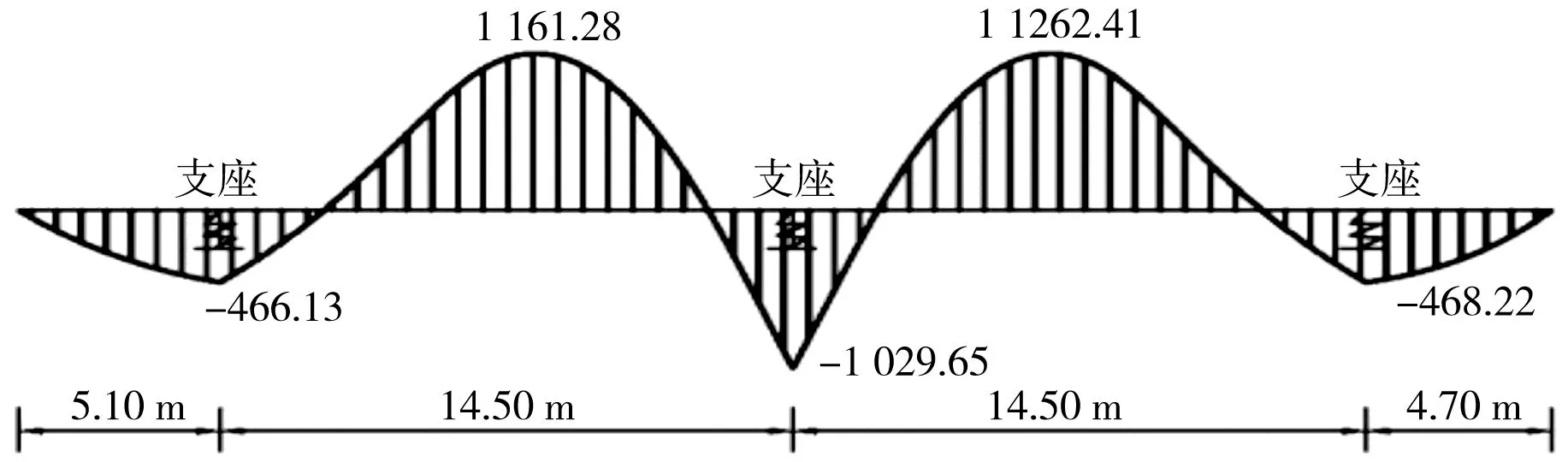
a)弯矩(单位：kN·m)

3.3 2种计算方法结果分析

分析计算图4、7内力、位移结果发现，结构力学法计算抗浮筏板结构的弯矩结果相对有限元方法小，结构剪力和位移则是有限元法大于结构力学方法。对比图4、7a，抗浮筏板中部支座弯矩相差很小，基本一致，但抗浮筏板左跨中部、右跨中部弯矩相差12%；抗浮筏板左、右两侧抗拔桩支座弯矩，结构力学方法小于有限元计算结果，主要原因在于结构力学简化将两侧抗浮筏板两端作为自由端考虑，实际筏板下部为地基土体，对筏板结构存在约束和弹性反力，反力作用两侧自由端筏板，产生叠加弯矩。

对比图4、7b，2种计算方法相差较大，原因在于中部抗拔桩长度仅20 m长，虽满足结构整体抗浮，但不能形成固定支座作用，在上浮荷载作用下，产生1.41 mm向上位移，使得筏板剪切作用下降，抗拔桩桩端剪力值相对较小。通过图4、7c对比，有限元计算结果板中位移相对较小，原因在于结构力学计算“门”式抗浮桩阀结构进行相应简化，整体刚度相对下降，特别是两端由于地基的支撑和反力，未发生位移。

4 结语

a)本文通过对深圳地铁9号线下穿某河道地铁隧道“门”式桩阀抗浮结构应用结构力学和有限元数值法分析结构在抗浮工况下内力和变形，2种计算方法结果表明其内力和变形规律性一致。结构力学方法小于有限元计算方法,主要支座和跨中弯矩最大相差12%；剪力和位移结构力学方法大于有限元计算方法，原因在于结构力学模型适当简化，且未考虑地基土体反力对筏板作用和抗拔桩在荷载作用下支座发生位移。

b)结构力学法计算“门”式桩阀抗浮结构内力和变形其相对精度不如有限元方法，但计算简便，计算结果表明抗浮筏板结构中部支座和隧洞上部筏板位置弯矩和有限元法相近，剪力和位移大于数值分析方法。基于结构力学方法能够在较短时间内得到结构主要部位弯矩相对准确、剪力和位移偏大，在项目前期立项、论证阶段可作为参考依据。

c)“门”式桩阀抗浮结构受多种荷载共同作用，边界条件复杂，有限元分析方法能够模拟在上浮工况下抗拔桩的桩土作用、地基对筏板反力作用、隧道上浮荷载对其上部土体挤压再作用于筏板，计算结果相对准确。因此对于“门”式桩阀抗浮结构可通过有限元数值方法准确计算，校核计算结果，指导优化设计。