地裂缝作用下管廊结构底部脱空范围计算方法
邓博团,田江涛,苏三庆,李 鑫,李 攀,王 劲
(1.西安科技大学 建筑与土木工程学院,陕西 西安 710054;2.西安建筑科技大学 土木工程学院,陕西 西安 710055;3.西安长庆科技工程有限责任公司,陕西 西安 710000)
地裂缝活动引起地下结构底部脱空是一种普遍现象.西安地裂缝分布广、规模大[1],地下管廊穿越地裂缝不可避免.而管廊穿越地裂缝时,管廊结构底部脱空对管廊结构受力变形模式起着决定作用,且对管廊建成后的运营造成极大的安全隐患,故对管廊结构底部脱空范围进行计算研究十分必要.
随着城市地下空间的开发和利用,许多学者对地下结构穿越地裂缝开展了大量研究.范文等[2-6]进行了有关地铁隧道的模型试验,从不同地裂缝角度、不同隧道截面形式、不同施工方法等方面对隧道的受力变形模式、破坏模式进行了研究,结果表明:采用不同几何相似比、不同隧道模型材料情况下,当地裂缝活动量达到一定量值时,隧道结构底部均有脱空现象出现.胡志平等[7]通过管廊斜穿地裂缝模型试验,认为管廊结构产生扭转的原因是由于脱空区范围的剪力流合力不通过结构截面的剪切中心造成的.门玉明等[8]在分析大量隧道过地裂缝模型试验结果的基础上,认为地裂缝的活动强度、隧道埋深、长度、土与隧道的刚度比等是影响隧道底部脱空区长度的主要因素,并总结了四种地铁隧道底部脱空的计算模型.刘东燕等[9]通过将脱空区三角形范围内的上覆土压力等效成一个过形心的集中力,求解箱型隧道过地裂缝的扭转解析解.梅源[10]通过数值分析研究发现,地裂缝沉降量达到一定值时管廊结构底部才出现脱空.王启耀[11]利用数值模拟研究了双舱综合管廊结构在地裂缝活动下的受力变形特征,发现管廊结构底部脱空区从上盘地裂缝处向上盘远端发展.以上无论是地铁隧道还是管廊方面的研究,虽然涉及到了结构底部产生脱空,但大多是定性描述和分析,缺乏对管廊结构底部脱空区范围的定量计算研究.
现有研究表明,对地下结构进行理论分析计算时,通常将其简化为置于弹性地基上的梁[12-15],但在地裂缝作用下,地下管廊结构底部出现脱空,这使得普通弹性地基梁理论的使用条件不再适用.弹性地基梁的使用条件是梁与地基连续接触,可看作是无穷多次超静定结构,在管廊底部脱空情况下,可将管廊与地基的接触看作有限次超静定结构.因此,计算管廊底部脱空范围,就是求解有限次超静定结构问题.
为此,基于Euler-Bernoulli-Bousslnesq模型和链杆法,通过建立管廊结构穿越地裂缝的底部脱空计算模型,给出管廊结构底部脱空区范围的计算方法.通过与既有管廊过地裂缝模型试验结果进行对比分析,验证管廊结构底部脱空区范围的计算方法的合理性和适用性.研究成果可为地裂缝区域管廊结构设计提供一定参考.
1 地下管廊结构的受力特性
已有的管廊穿越地裂缝的模型试验结果表明[7],在上盘沉降初期,管廊上覆荷载均匀分布,随着上盘沉降量增加,管廊顶部接触压力发生改变,表现为上盘增大,下盘减小,说明作用于地裂缝两侧管廊上的外荷载并不会随着地裂缝的活动而变化,变化的是作用于管廊上的土压力.管廊底部接触压力总体表现为上盘减小,下盘增大,管廊与下盘土层始终接触;管廊变形主要表现为下盘底部受压,上盘底部受拉,且靠近地裂缝处下盘管廊变形较大,远离地裂缝处趋近于零.而上盘管廊由于土体沉降产生的拖拽作用,与土体发生整体沉降,在管廊底部形成局部脱空.管廊结构变形受力示意图如图1所示.
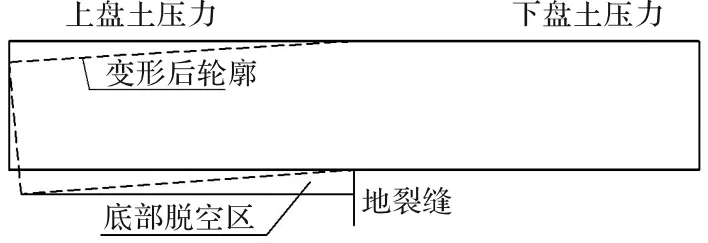
图1 管廊结构纵向受力图
2 底部脱空计算模型
由管廊的受力特性可知,在管廊穿越地裂缝模型试验中,随着地裂缝上盘相对下降,下盘始终与地基接触,下盘管廊在地裂缝处变形最大,远离地裂缝变形趋近于零,因此可以将下盘土层对远离地裂缝的管廊端部约束简化为固定端.当上盘沉降量达到一定值时,上盘管廊随土体一起发生沉降变形,由于管廊与周围土体变形的不协调,在上盘管廊底部形成脱空区,因此可将土层对上盘管廊端部的约束简化为定向支座,为简化计算,不考虑管廊顶部接触压力的变化,按上覆荷载q0计算,如图2所示.

图2 管廊结构底部脱空计算模型
计算上盘管廊底部脱空范围,由于下盘始终与地基接触,故只考虑上盘管廊的情况.将位于地裂缝上盘的管廊简化为Bousslnesq地基中的Euler-Bernoulli梁,简称为Euler-Bernoulli-Bousslnesq模型(EB-B模型),用链杆法的原理,将上盘管廊与地基接触的部分用n个链杆连接,计算模型可简化为如图3所示,xt为管廊上盘结构底部脱空区范围,c为相邻链杆的间距,ak为第1个链杆与第k个链杆间的间距,pn为管廊与地基相互作用力.Δ1为上盘管廊结构端部位移,Δ2为地裂缝错动量.
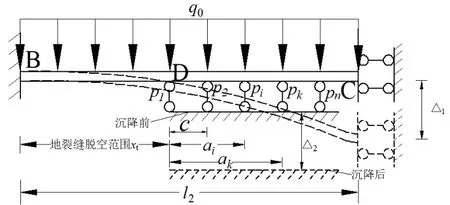
图3 管廊结构脱空简化计算图
Δ1、Δ2有这样的关系:一是上盘管廊结构端部位移Δ1随地裂缝错动量Δ2的增大有增大的趋势,二是管廊结构本身的抗弯刚度有阻碍管廊结构端部位移Δ1增大的趋势,经过查阅数学手册可得符合Δ1、Δ2关系的函数为双曲正切函数,经过拟合可得符合要求的函数如图4所示.
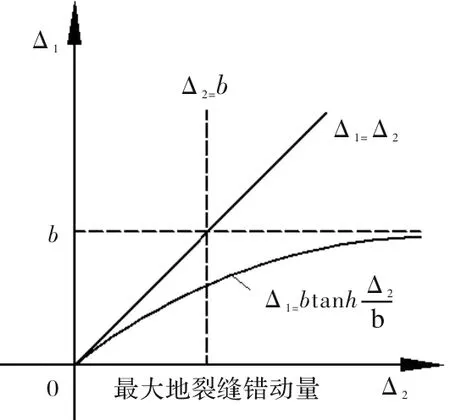
图4 Δ1、Δ2函数关系曲线图
则有
(1)
3 管廊结构底部脱空范围计算推导
在管廊结构底部完全脱空前,管廊结构与地基的接触部分的相对位移为零,即任意链杆k处管廊结构和地基的相对位移Δk=0.为求解Δk,将图3所示超静定结构取作以B点为固定端的悬臂梁结构作为基本体系,则任意链杆k处管廊结构和地基的相对位移Δk由四种外荷载引起:地基反力在上盘未脱空区引起的位移Δkpi,上覆荷载在管廊结构k点引起沿pk方向的挠度Δkq,上盘管廊结构端部弯矩MC在管廊结构k点引起沿pk方向的挠度ΔkMC,由上盘管廊结构端部垂直位移Δ1在管廊结构k点引起的挠度Δk1.则有
Δk=Δkpi+ΔkMC+Δkq+Δk1=0
(2)
现在对式(2)中各分项进行求解.
①Δkpi是任一点i的管廊与地基相互作用力pi在k点地基产生的沉降值和在管廊k点作用产生的挠度之和.即
(3)
式(3)中:δki为pi=1时k点地基产生的沉降值yki和管廊上盘结构k点产生的挠度vki之和,即δki=yki+vki.
求yki可以将荷载pi=1看作以i点为基点,长度为c的区间上荷载集度为q=1/c的均布荷载,距k点r处取微段dr,微段上的荷载dp=(1/c)dr,微段荷载与基点i的距离为d=r-x,如图5所示.
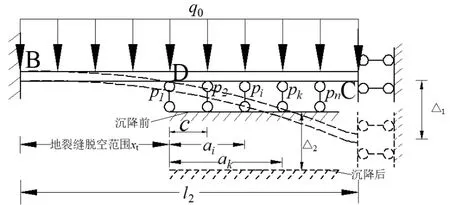
图5 沉降计算模型
由集中力作用下的沉陷公式可得微段荷载作用下k点的相对位移为
(4)

整个荷载段在k点产生的相对位移为
(5)
求解积分得
(6)
式中,Fki=clnc-cln(x-c)-xlnx+xln(x-c).为便于计算,对lnc,ln(x-c)展开幂级数,假定0 求vki为上盘管廊结构在地基反力pi=1作用下k点产生的挠度,由结构力学挠度公式可得 (7) 则得 (8) 由式(6)、(8)可得 (9) ②求MC对上盘未脱空区管廊结构k点产生的位移ΔkMC,可用结构力学挠度积分公式计算得 (10) ③Δkq为上盘上覆荷载对未脱空区管廊结构k点产生的位移,可由结构力学挠度积分公式得 (11) 式中:MC=Rθc,θc为构件端部相互之间的角位移;R为节点的连接刚度,R=E1I. ④上盘管廊结构端部C点的垂直位移相对上盘管廊结构长度是一个微量,故上盘管廊结构端部C点的垂直位移引起未脱空区任意一点k的向下的垂直位移Δk1可直接使用几何方法求解.得 (12) 综上,将式(3)、(10)、(11)、(12)代入式(2),得到含xt的非线性方程组. 此外,由上盘管廊结构满足静力平衡条件,对B点取矩,则有 xtp1+(xt+a2)p2+…+(xt+ak)pk+…+(xt+ an)pn-Mq+MC=MB=θBE1I (13) 式中:Mq为上盘管廊结构上覆荷载对管廊结构端部B点的弯矩Mq=(q0/2)l22;θB为B点的角位移. 同时,上盘管廊结构端部还满足端部约束条件: (14) (15) 计算管廊底部脱空范围xt,取不同地裂缝沉降量Δ2,代入式(1),得到Δ1,将之代入式(15),得到θB,将θB代入式(14),得到θC.然后通过式(2)、(13)构建方程组,式(2)中各项最高次幂为四次,式中存在非线性项,因此很难直接得到解析解,可利用MATLAB中的相关函数将非线性方程转化为线性方程,即可求解得到管廊底部脱空范围xt的值. 为了验证管廊结构底部脱空范围计算方法的合理性,采用文献[7]中地裂缝作用下1∶15管廊模型试验与本文计算模型进行对比分析.模型试验基本参数如下:模型管廊长5 m,管廊截面为0.56 m×0.313 m,上盘管廊长度2.175 m,模型材料的弹性模量为8.41×103MPa,模型围岩地基由杂填土、黄土、粉质黏土分层填筑而成,重度取为18.7 kN·m-3,弹性模量取为31.08 MPa,泊松比为0.25,地裂缝最大沉降量0.08 m,上覆土1 m,允许缝宽S=30 mm,管廊结构截面宽度D取0.56 mm.计算时链杆数n取30,满足计算精度要求.由MATLAB计算得到管廊底部脱空范围的理论计算值,如表1所示,与模型试验所得管廊底部脱空值进行对比,见表2. 表1 管廊结构底部脱空范围的理论计算值 表2 计算值与试验值对比分析 由对比分析结果可知,管廊底部脱空范围计算方法所得结果与模型试验结果基本一致,最大误差不超过-18.75%. (1)基于Euler-Bernoulli-Bousslnesq模型和链杆法,通过将脱空情况下的管廊转化为有限次超静定结构,建立了管廊结构穿越地裂缝的底部脱空计算模型,提出了管廊结构底部脱空范围的计算方法. (2)通过与模型试验进行对比分析,表明计算结果和模型试验结果基本一致,最大误差不超过-18.75%.说明本文提出的管廊底部脱空范围计算方法具有一定的合理性和适用性.求解管廊底部脱空范围后,可以通过求解有限超静定结构,得到不同地裂缝沉降量下管廊的弯矩剪力,为地下管廊的结构设计提供一些参考. (3)在建立计算模型时,本文将管廊简化为Bousslnesq地基中的Euler-Bernoulli梁,只考虑了弯矩对管廊变形的影响,而忽略了剪力对其变形的影响,在后续研究中,将同时考虑弯矩和剪力对管廊变形的影响,通过对管廊在Winkler地基模型、Pasternak地基模型中简化为Timoshenko梁的情况与本文研究进行对比分析,优化管廊底部脱空范围的计算方法.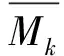

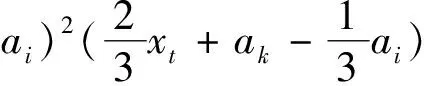



4 模型验证


5 结果与讨论

