基于动态密钥的彩色图像扩散加密算法

董小雨，冯秀芳

(1.太原理工大学 信息与计算机学院，山西 晋中 030600；2.太原理工大学 软件学院，山西 晋中 030600)

0 引 言

对图像的加密算法的研究成为图像加密[1-4]领域的研究热点，彩色图像加密[5-8]、多图像加密、混沌图像加密[9-12]等图像加密方法被学者所提出。当前，图像加密算法中普遍使用置乱、扩散两个阶段对图像进行加密。在加密算法中，有学者提出异或、加取模、移位等循环扩散加密方法。例如，多次异或运算实现对图像的扩散操作[13]。有学者提出增加对像素值的不同数学运算操作，例如，将超混沌系统与移位密码结合对像素位置加密、扩散和混淆像素值[14]。也有学者提出在对图像置乱的同时实现扩散的加密方法。例如，在传统图像加密算法基础上，增加置乱和扩散的耦合性，实现多混沌结合的快速图像加密[15]。

近年来，学者们提出的通过循环数学运算、增加新的操作或多种操作的融合提高加密算法的复杂度。但从为建立各像素值之间关联的角度，传统的扩散算法一般使用当前明文像素值、与当前明文像素相邻的密文像素值、混沌序列之间进行相互运算，加密过程中参数不变，有限次加密得到的加密图像之间具有较强的规律性，抗攻击能力较差。为处理这些问题，本文提出一种基于动态密钥的加取模扩散加密算法，进行可变控制参数的图像加密。在置乱阶段，首先使用Hilbert曲线置乱图像，将相邻像素进行重新组合，减少图像中不动点数量；其次使用Arnold随机矩阵对图像每一像素进行选择性置乱。在扩散阶段使用基于动态密钥的加取模扩散算法，将图像之间的差异程度对扩散过程中混沌序列的初始参数、扩散初始值、扩散序列等参数进行调整，实现扩散加密过程参数的改变。通过该加密方法，加密任意两幅图像使用的密钥，加密过程中的参数都不相同，可有效提高明文敏感性。

1 系统模型及相关概念

在本文的加密系统中，使用Hilbert曲线置乱、Arnold置乱等置乱方法，结合提出的基于动态密钥的加取模扩散算法对图像进行加密。本节介绍Hilbert曲线置乱、Arnold变换、基于动态密钥的加取模扩散的基本思路。

1.1 Hilbert曲线置乱

二维Hilbert曲线可以描述为，将一个正方形以一定的规则进行遍历，可得到一条填满整个正方形的曲线。在本文中，按二维Hilbert曲线遍历的顺序对二维图像的像素点进行扫描存储，按列排列得到Hilbert曲线置乱图像，实现图像置乱处理。加密算法中使用Hilbert曲线遍历图像以减少不动点的数目。Hilbert置乱加密过程如图1所示。

图1 Hilbert置乱加密过程

1.2 Arnold变换

Arnold置乱是基于矩阵变换的算法。首先对像素点做x轴方向的变换，再做y轴方向的变换，最后做取模运算，将图像内的离散像素点进行重新排列。

Arnold变换公式如式(1)所示

(1)

Arnold变换通过使用2×2的矩阵R，对原图像像素点的坐标位置(x0,y0)进行变换，得到变换后图像像素点的坐标位置(x1,y1)，M、N表示图像矩阵大小。

Arnold矩阵R如式(2)所示

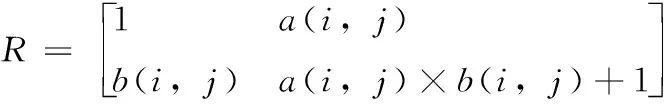
(2)

矩阵R中a(i,j)、b(i,j) 表示Arnold变换参数。本文中a(i,j)、b(i,j) 的取值为混沌系统得到的随机序列X值。对图像中每一像素使用Arnold矩阵R进行变换，对 (i,j) 位置的像素点进行置乱使用的参数为a矩阵中的 (i,j) 点的随机序列值和b矩阵中的 (i,j) 点的随机序列值。使用Arnold 变换进行置乱的矩阵a、b如图2所示。

图2 随机矩阵a，b转换

Arnold置乱加密算法见表1，Arnold置乱解密算法见表2。

表1 置乱加密算法

表2 置乱解密算法

1.3 基于动态密钥的加取模扩散

在图像扩散加密中，通过改变像素点的灰度值使得任一像素点的像素值信息影响尽可能多的其它像素点的像素值。设明文图像为8 bit的图像，基于动态密钥的加密模扩散算法如式(3)所示

Ci=(Ci-1+Si+Pi+Ki×V)mod256

(3)

在基于动态密钥的加取模扩散算法中，明文图像被展开成一维向量，记为Pi，i=1,2,…,MN； 相应的密文也为一维向量，记为Ci，i=1,2,…,MN； 初始值C0来自密钥；Si，Ki为密码向量，i=1,2,…,MN；V为图像的一个特征值Fp与衡量图像的差异值E之差，作为扩散算法的初始值和参数。

在基于动态密钥的加取模扩散算法中，扩散阶段使用混沌序列Ki与扩散阶段初始值V的乘积作为扩散阶段的一个参数对扩散过程进行调整，同时将图像之间的差异值E对扩散阶段中的混沌序列Ki的初始参数K={x0,y0,z0,w0} 进行调整，扩大图像差异对扩散过程的影响，提高明文敏感性。采用式(3)所示的运算进行扩散处理，其扩散加密算法，解密算法见表3，表4。

表3 扩散加密算法

表4 扩散解密算法

2 加密算法

2.1 加密算法的过程

本文提出的加密算法中，使用Hilbert曲线和Arnold随机矩阵对图像进行置乱。在扩散阶段使用基于动态密钥的加取模扩散算法进行加密。加密算法的过程如图3所示，解密过程为加密算法的逆过程。

图3 加密算法的过程

2.2 基于动态密钥的加取模扩散加密算法

以彩色Lena图像为例，扩散加密流程如下列步骤所示：

(1)将彩色图像分解为红，绿，蓝这3个通道的图像，分别为P-R,P-G,P-B。

(2)将红，绿，蓝这3个通道的图像P-R,P-G,P-B进行Hilbert置乱，使用二维Hilbert曲线遍历图像得到P-R1,P-G1,P-B1。

(3)使用超混沌Lorenz系统的初始值作为密钥，通过超混沌Lorenz系统得到随机序列X，将随机序列X转换为两个M×N大小矩阵P1、Q1作为Arnold置乱的初始矩阵参数a、b矩阵，Arnold置乱矩阵R中的a(i,j) 和b(i,j) 分别为P1(i,j)、Q1(i,j)， 使用式(1)对Hilbert置乱3个通道的图像P-R1,P-G1,P-B1进行Arnold置乱得到P-R2,P-G2,P-B2。

(4)使用式(4)计算，将彩色图像每一通道的图像的像素值P(i,j) 累加和对256取余得到的值Fp分别作为图像三通道的特征值R-Fp,G-Fp,B-Fp，使用式(5)以该特征值与常数T(密钥)之间的差作为不同图像之间的差异程度R-E,G-E,B-E，使用式(6)将特征值Fp与差异程度E的差值作为扩散阶段的初始值R-V,G-V,B-V

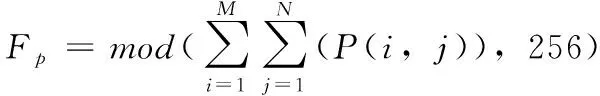
(4)

E=T-Fp

(5)

V=Fp-E

(6)

(5)超混沌Lorenz系统的初始值S={x0,y0,z0,w0} 作为密钥，通过超混沌Lorenz系统得到随机序列Si,i=1,2,…,MN。 将图像之间的差异值E对扩散阶段中的混沌序列的初始参数K={x0,y0,z0,w0} 以式(7)进行调整，通过超混沌Lorenz系统得到随机序列Ki,i=1,2,…,MN。 实现对扩散阶段密钥的调整

x0=x0+E×10-10
y0=y0+E×10-10
z0=z0+E×10-10
w0=w0+E×10-10

(7)

(6)对Arnold置乱3个通道的图像P-R2,P-G2,P-B2 分别展开成一维向量，记为Pi,i=1,2,…,MN。 使用本文提出的扩散算法进行加取模正向、逆向扩散操作得到图像P-R3,P-G3,P-B3。实现对扩散过程参数的调整。

(7)将置乱、扩散加密处理的3个通道的图像P-R3,P-G3,P-B3混合为彩色图像得到加密彩色图像。

以彩色Lena图像的红色通道图像Lena-R为例，基于动态密钥的加取模扩散加密算法流程如图4所示。

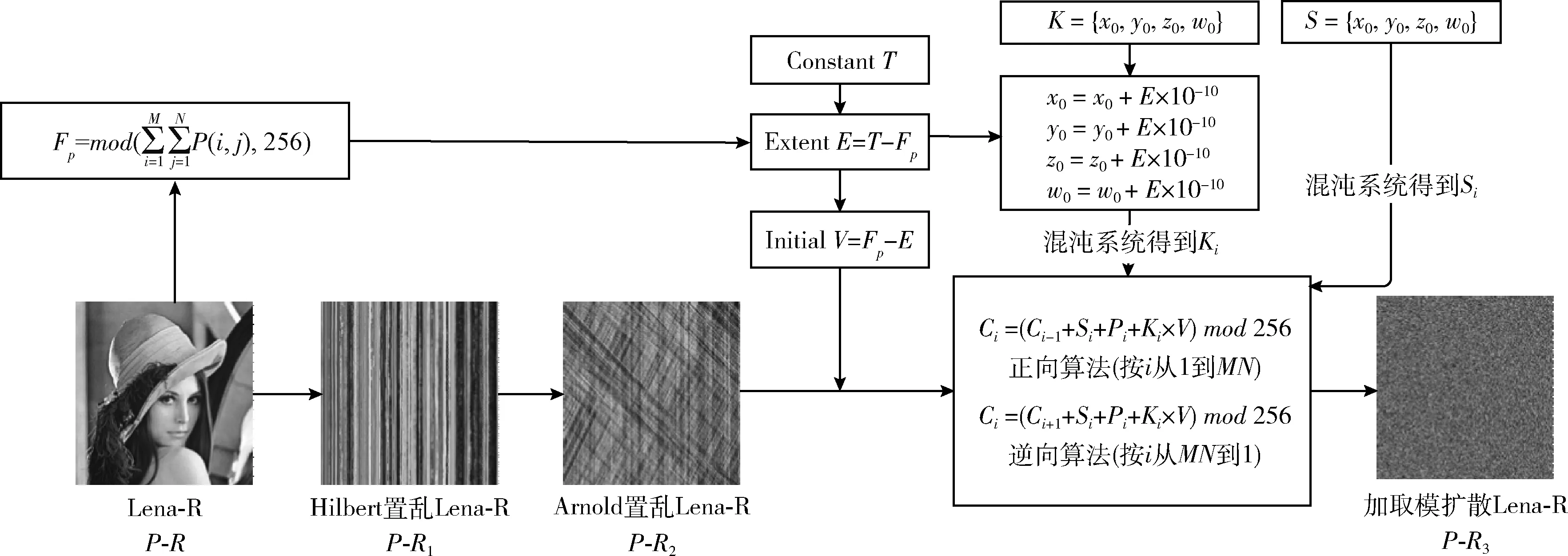
图4 基于动态密钥的加取模扩散加密算法流程

2.3 基于动态密钥的加取模扩散解密算法

解密算法与加密算法的过程相反，对彩色图像的每个通道的图像先进行加取模扩散的还原，再进行Arnold置乱和Hilbert置乱的还原。在接收方接收到密文和密钥进行图像解密时，加取模扩散、Arnold置乱和Hilbert置乱解密的过程如下：

(1)使用式(5)以密钥中衡量图像变化程度的常数T与彩色图像三通道的特征值R-Fp,G-Fp,B-Fp分别进行差值计算得到3个通道图像之间的差异程度R-E,G-E,B-E，使用式(6)将彩色图像三通道的特征值R-Fp,G-Fp,B-Fp与差异程度R-E,G-E,B-E的差值作为逆向加取模扩散的初始值R-V,G-V,B-V。

(2)使用密钥中超混沌Lorenz系统的初始值S=

{x0,y0,z0,w0}， 通过超混沌Lorenz系统得到随机序列Si,i=1,2,…,MN。 将图像之间的差异值E对扩散阶段中的混沌序列的初始参数K={x0,y0,z0,w0} 以式(7)进行调整，通过超混沌Lorenz系统得到随机序列Ki,i=1,2,…,MN。 实现对逆向扩散阶段密钥的调整。

(3)分别取加密图像3个通道的图像P-R3,P-G3,P-B3，将其展开成一维向量，记为Pi,i=1,2,…,MN。 使用本文提出的扩散算法进行加取模正向、逆向的反向扩散操作得到图像P-R4,P-G4,P-B4。实现对扩散逆过程参数的调整。

(4)使用超混沌Lorenz系统的初始值作为密钥，通过超混沌Lorenz系统得到随机序列X，将随机序列X转换为两个M×N大小矩阵P1、Q1作为Arnold置乱的初始矩阵参数a和b矩阵，Arnold矩阵A中的a(i,j) 和b(i,j) 分别为P1(i,j)、Q1(i,j)， 使用式(1)对逆向扩散解密3个通道的图像P-R4,P-G4,P-B4进行Arnold置乱还原得到P-R5,P-G5,P-B5。

(5)将Arnold置乱还原得到的红，绿，蓝这3个通道的图像P-R5,P-G5,P-B5进行Hilbert置乱还原，使用二维Hilbert曲线逆向遍历图像得到P-R6,P-G6,P-B6。

(6)将二维Hilbert曲线逆向遍历图像得到P-R6,P-G6,P-B6图像作为红，绿，蓝这3个通道的图像，将三通道图像融合得到彩色图像。以彩色Lena图像的红色通道图像Lena-R为例，基于动态密钥的加取模扩散解密算法流程如图5所示。

图5 基于动态密钥的加取模扩散解密算法流程

在传统的图像加密算法中，通过像素改变率(number of pixels change rate，NPCR)和归一化像素值平均改变强度(unified average changing intensity，UACI)的值来衡量明文图像像素值的微小改变对加密图像的影响。本文提出的扩散加密算法与传统的扩散加密算法相比，加密任意两幅图像，即使相差一个比特值的两幅图像，使用的加密密钥，加密过程中的参数都不相同。实验结果表明对原始图像进行微小的改变，通过一次加密，加密图像会在大范围内改变，UACI、NPCR即可达到理论值，可有效抵抗选择明文攻击，使加密系统具有较强的明文敏感性，提高了加密的安全性。

3 加密效果分析

本节对加密算法的性能进行分析，在实验中采用图像直方图分析、相关性分析、明文敏感性、密钥敏感性、信息熵和鲁棒性分析对Lena的红、绿、蓝这3个通道图像加密效果进行分析，采用NPCR、UACI等对图像加密效果进行定量分析。

3.1 实验结果

图6(a)、图6(b)、图6(c)显示了Lena彩色图像、加密、解密结果。直观上可以看到密文图像变得模糊不清，在解密后可以无损还原图像。

图6 加密，解密图像

3.2 密钥空间

图7显示了本文加密系统的密钥，密钥为彩色图像三通道的特征值R-Fp,G-Fp,B-Fp，一个衡量图像变化程度的常数T，超混沌Lorenz系统的初始值S={x0,y0,z0,w0}，K={x0,y0,z0,w0}， 其中x0∈(-40,40),y0∈(-40,40),z0∈(1,81),w0∈(-250,250)，x0,y0,z0的步长为10-13，w0的步长为10-12。所以本文加密算法的密钥空间足够大，可有效抵抗暴力攻击。

图7 加密系统密钥

3.3 直方图分析

图8(a)、图8(b)、图8(c)分别为Lena红色通道图像、Lena红色通道图像直方图、加密图像直方图分析结果。直观上密文图像具有平坦的直方图，明文图像的直方图跌宕起伏。

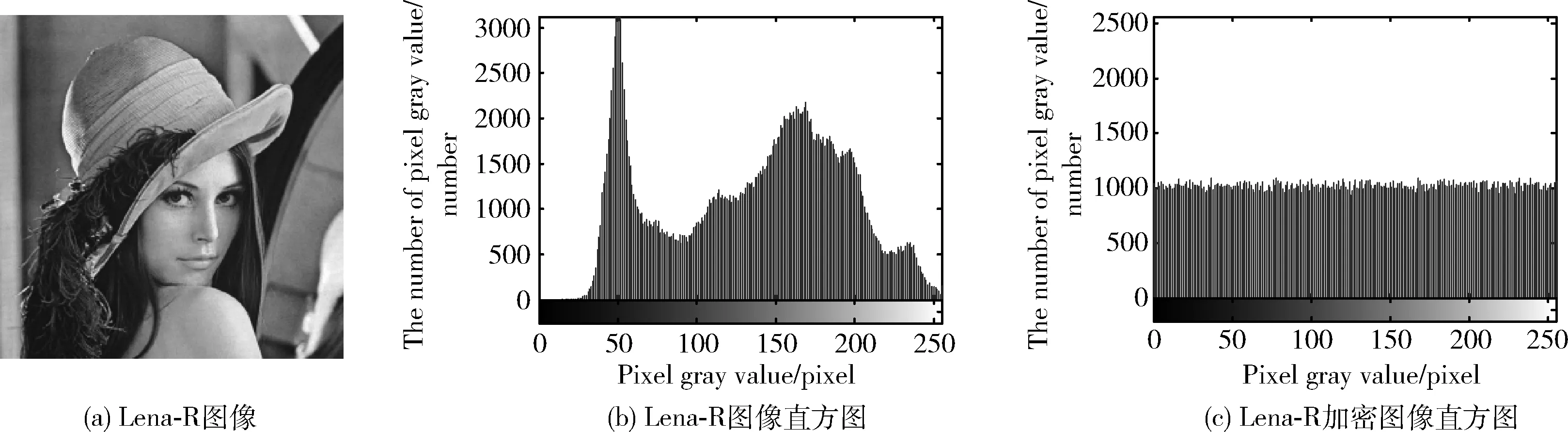
图8 加密，解密图像直方图

3.4 相关性分析

对明文图像与密文图像进行相关性比较。设从需要考察的图像中任取N对像素点，记它们的灰度值为 (ui,vi)，i=1…N， 向量u={ui} 和v={vi} 间的相关系数计算公式如下

(8)

图9(a)～图9(f)分别为Lena红色通道图像Lena-R和密文图像在水平、垂直、正对角方向上随机选取10 000对相邻像素点的相关性分析结果。直观上明文图像在水平、垂直、正对角方向上具有较强的相关性，密文图像相关性较差。

图9 Lena-R加密，解密图像相关性分析

从Lena的红、绿、蓝这3个通道的明文图像和密文图像中随机选取10 000对相邻像素点，计算水平、垂直、对角方向上的相关系数。如表5所示，明文图像的相关系数接近于1，密文图像的相关系数接近于0。

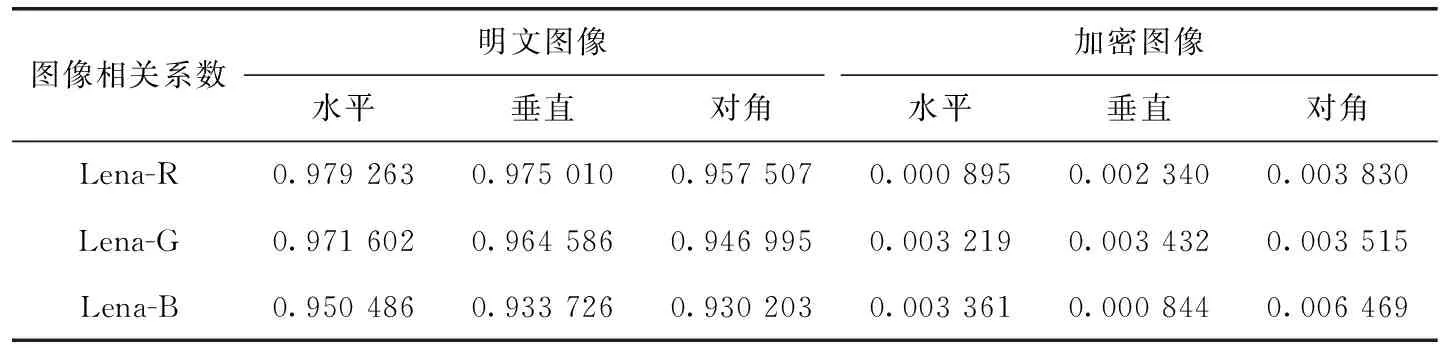
表5 Lena-R、Lena-G、Lena-B加密，解密图像相关系数

3.5 明文敏感性分析

本文采用NPCR和UACI来衡量同一密钥对差别微小的两个明文图像加密得到的密文图像之间的差别，进行明文敏感性分析。定义为式(9)和式(10)

(9)

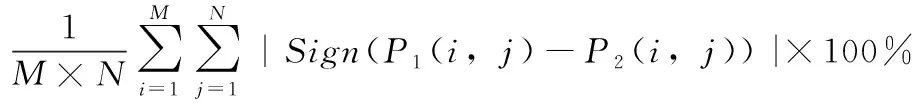
(10)

实验中对Lena图像的红，绿，蓝这3个通道分别选取像素值微小差异的图像进行明文敏感性分析，计算任意一个像素点相差为1到20像素值的两幅图像通过本文加密算法得到的加密图像之间的NPCR和UACI值。

图10显示了计算Lena图像的3个通道图像在随机改变1个像素的加密图像与初始加密图像之间的NPCR、UACI值，计算结果接近于NPCR、UACI的理论值99.6094%和33.4635%。实验结果表明，两个差别微小的明文图像加密后得到相应的密文图像相差迥异，它们的NPCR、UACI计算结果与其理论值相近。

图10 NPCR和UACI值

3.6 密钥敏感性分析

以明文图像Lena的红、绿、蓝这3个通道图像为例，采用图像加密系统分析当密钥发生微小变化时，加密同一明文图像得到的两个密文图像的差别，分析密钥敏感性。密钥为超混沌Lorenz系统的初始值即S={x0,y0,z0,w0}，K={x0,y0,z0,w0}，x0∈(-40,40)，y0∈(-40,40)，z0∈(1,81)，w0∈(-250,250)， 其中x0,y0,z0的步长为10-13，w0的步长为10-12。对于密钥S、K，随机从其密钥空间中选取10个值，进行如下实验：对于每一组密钥，保持y0,z0,w0不变，改变x0的值，改变的量为10-13，使用改变x0前后的密钥加密同一明文图像，计算两个密文图像之间的NPCR、UACI值。计算10次实验得到NPCR、UACI的平均值。对于密钥y0,z0和w0进行同样实验计算平均值，其中y0,z0改变的量为10-13，w0改变的量为10-12。

表6显示了改变密钥x0,y0,z0,w0，计算Lena红、绿、蓝这3个通道图像的加密图像的NPCR、UACI值，与NPCR、UACI的理论值非常接近，反映了两个密文图像差异显著，即密码系统具有较强的密钥敏感性。

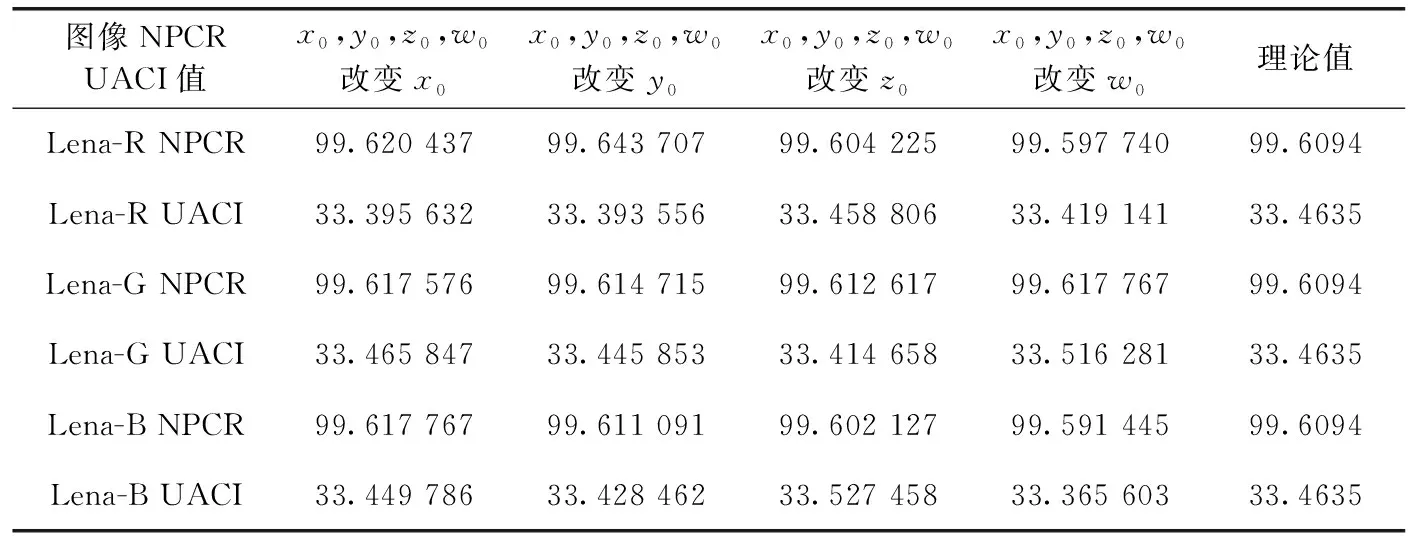
表6 改变密钥的Lena-R、Lena-G、Lena-B的NPCR、UACI值比较

3.7 信息熵

信息熵反映了图像信息的不确定性，一般认为，熵越大，不确定性越大。计算公式如式(11)所示

(11)

L为图像的灰度等级，p(i) 为灰度值i出现的概率。对于L=256的灰度图像，H的理论值为8。从表7中可以看出Lena红、绿、蓝这3个通道加密图像的信息熵非常接近于8。

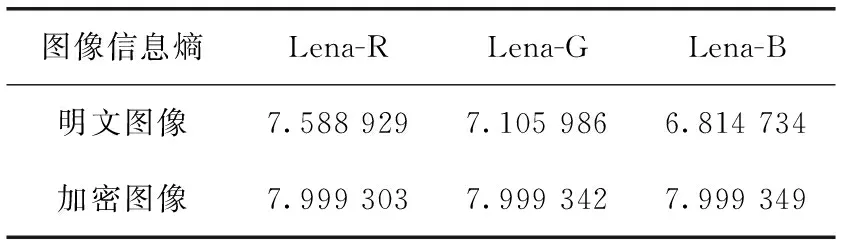
表7 Lena-R、Lena-G、Lena-B的加密、解密图像信息熵

3.8 鲁棒性分析

衡量一个加密系统的抵抗干扰能力最重要的标准是鲁棒性分析，本文以Lena图像进行实验，分别通过噪声攻击和剪切攻击测试算法的鲁棒性。图11(a)、图11(b)显示了对添加10倍高斯白噪声攻击的加密图像以及解密结果，图11(c)、图11(d)显示了剪切攻击加密图像以及解密结果。实验结果显示了本文算法可以在一定程度上抵抗噪声攻击和剪切攻击。若密文传输中出现传输错误，解密系统可以应对。

图11 鲁棒性分析

4 结束语

针对同一加密系统，不同图像加密时加密密钥不变，加密过程控制参数不变等规律性的问题，提出一种基于动态密钥的彩色图像扩散加密算法。算法新颖之处在于通过Arnold随机矩阵对图像中每一像素点位置进行随机置乱，同时使用不同图像之间的差异程度对扩散过程中混沌系统的初始参数进行调整，实现加密密钥的改变，调整扩散过程的初始值，扩散序列等参数。通过加入待加密图像特征值对图像扩散过程进行扰动，使得图像加密过程与动态密钥相关联，进行可变控制参数的数字图像加密。实验结果表明，本文提出的加密算法可有效提高明文敏感性，加密算法具有较高的安全性。