逐步回归分析中国煤质特性与其液化特性关系

颜丙峰， 王光耀， 朱肖曼， 史士东

(煤炭资源高效开采与洁净利用国家重点实验室，北京 100013)

煤液化的反应性能与煤种有很大关系，研究煤种各种性质与其液化性能关系，是评选液化用煤的基本方法[1]。煤的灰分、挥发分、元素组成、岩相组成(镜质组、壳质组、惰质组、最大镜质体反射率)等煤质特性不仅会对其液化性能、液化工艺产生重要影响[2-5]，还会影响液化产品的经济效益。一般而言，挥发分含量越高、H/C原子比越大、惰质组含量越小的煤种，其变质程度越低，越容易液化。但煤变质程度越低，其氧元素含量会越高，导致其液化水产率和氢耗提高。

煤的液化特性通常与多个煤质特性呈线性关系。Garr等[6]发现煤的灰分含量及C、H元素含量与煤的转化率线性相关；Lee等[7]发现煤的灰分含量与煤的转化率线性相关；李小彦等[8-9]发现煤的转化率与挥发分、H/C原子比、活性组分含量分别成线性关系。然而，这些多是针对特定煤种且专注于煤质特性与其液化转化率、产率的关系，而对煤质特性与其液化过程中水、气产率及氢耗等关系的研究较少。

对煤质特性与煤的液化性能关系的研究多采用多元线性回归分析方法。多元线性回归分析过程中，回归方程中的自变量越多、剩余标准差越小，回归方程效果越好、精度越高，因此希望“最优”回归方程中包含尽可能多的自变量，特别是对因变量有显著影响的自变量不能遗漏[10]。但是，若回归方程包含的自变量过多，可能会导致自变量之间存在多重共线性，造成对因变量有显著影响的自变量被判定为无显著影响，导致有用的自变量被错误剔除，使模型与实际相差甚远[11]。因此，必须采取有效方法消除自变量间多重共线性的影响。最常用的消除多重共线性的方法有主成分分析法[12-14]和逐步回归法[15-18]。主成分分析法的目的在于降维，将原有指标进行线性组合，减少指标个数；而逐步回归法的目的是剔除影响不显著的指标，而保留原有指标中影响显著的若干指标。

20世纪80～90年代，北京煤化学研究所对中国120多种煤进行筛选[19]，得到16种适合液化的中国煤种，并给出其煤质分析和液化结果[3,19]。在这些实验数据的基础上，笔者使用SPSS 22.0软件建立上述16种煤种(共计24组数据)煤质特性与其液化特性间的多元线性回归模型，采用多元线性回归与逐步回归分析相结合的方法，筛选对其液化特性影响显著的煤质特性，并以文献[20-24]中的相关数据验证逐步回归关系式的可靠性。

1 煤质特性对液化特性的影响分析

1.1 煤质特性与液化特性的相关性分析

为了建立多元线性回归模型，需首先考察哪些煤质特性与其液化特性具有线性相关性，因此笔者筛选12种煤质特性与6种液化特性指标间的线性相关性。其中，煤质特性指标包括挥发分质量分数(X1)，C、H、N、S、O元素的质量分数(X2～X6)，H/C和O/C原子比(X7和X8)，镜质组、壳质组、惰质组体积分数(X9～X11)和最大镜质体反射率(Rmax，X12)；液化特性指标包括煤转化率(Y1)、油产率(Y2)、水产率(Y3)、气产率(Y4)、沥青质产率(Y5)、氢耗(Y6)。

采用软件SPSS 22.0进行煤质特性与液化特性间相关性的分析[25-26]，结果见表1。其中，R为Pearson相关系数，R绝对值越大，说明煤质特性与液化特性的线性相关程度越高。P为确认关联结果有效的犯错概率(P=0.05表示有5%的变量关联可能是偶然性造成的)，P越大，则变量关联可靠性越差。在相关性分析中，P可以用来判断线性相关的显著性。通常P≤0.01，表示液化特性与煤质特性线性相关很显著；0.010.05，表示液化特性与煤质特性无相关性。

由表1可以看出：煤转化率与C和O元素含量、O/C原子比、惰质组含量的P均不大于0.01，R也较大，说明其相关性很显著；而与镜质组含量、Rmax(X12)的P在0.01～0.05范围内，说明其相关性较显著。同理，油产率只与H元素含量显著相关；水产率与C和O元素含量、O/C原子比、Rmax的相关性很显著，而与挥发分、H元素含量，镜质组、惰质组含量相关性较显著；气产率与C和O元素含量、O/C原子比、镜质组和惰质组含量、Rmax的相关性很显著，而与挥发分、S元素含量的相关性较显著；沥青质产率与挥发分含量、C和O元素含量、O/C原子比、Rmax相关性很显著，与H/C原子比相关性较显著。氢耗与N元素含量相关性很显著，与C和O元素含量、O/C原子比、镜质组含量、Rmax相关较显著。

此外，煤转化率、水产率、气产率、氢耗与C元素含量、Rmax成负相关，与O元素含量、O/C原子比成正相关，而沥青质产率则相反，与C元素含量、Rmax成正相关，与O含量、O/C原子比成负相关。

表1 煤质特性与液化特性的相关性分析结果Table 1 Correlation analysis of coal characteristics and liquefaction properties

1.2 煤质特性与煤转化率回归分析

由线性相关性分析可知，X2、X6、X8、X9、X11、X12可能是影响Y1的因素。因此以X2、X6、X8、X9、X11、X12为自变量，Y1为因变量，用SPSS 22.0软件建立多元线性回归模型[27-29]对其进行回归拟合，其中置信区间为95%水平[30]，结果见表2模型Z1；在多元线性回归模型的基础上，采用逐步回归分析法，在显著性水平α=0.10下剔除不符合显著性要求的变量，得到2种逐步回归分析模型(模型Z2和Z3)。其中F为回归模型方差与残差的比值，是模型的整体检验。F通常要与其临界值Fα作比较，其中α为显著性水平，取α=0.05；若F>Fα，表示模型是可靠的；反之则没有统计学意义。T检验是对单个自变量的显著性检验。B为各自变量在回归方程中的系数，Beta为标准回归系数。方差膨胀因子(VIF)代表各自变量的多重共线性，一般若VIF>10 则说明各自变量之间存在较强的多重共线性。

由表2可以看出，模型Z1的Pearson相关系数R=0.768，修正决定系数Adj-R2为0.444，说明模型线性拟合效果较好。模型Z1的F0.05=2.699，F检验值为4.063，因此F>Fα，说明该多元回归模型可靠；而且，其P为0.01，表明Y1与X2、X6、X8、X9、X11、X12等6种煤质特性的线性关系很显著。得到回归方程为：

Y1=70.719+0.512X2-1.808X6+181.475X8-0.109X9-0.236X11-7.886X12

(1)

式(1)中不同自变量的取值范围和量化程度是不同的。例如：C质量分数的取值范围为0～1，O/C原子比的取值范围为0～0.4。若C质量分数和O/C原子比均由0增至0.4，二者变化数值一样，但增幅不同。前者增幅为40%，后者增幅达100%，从而导致无法直接用系数B判断哪个自变量对因变量影响程度更大。因此，需要将数据标准化，即将原始数据减去相应变量的均数后再除以该变量的标准差，得到采用标准化回归系数(Beta)的标准化回归方程。Beta系数的绝对值越大，自变量对因变量的影响越大。由表2的Beta系数可知，影响煤转化率从大到小的因素依次为O/C原子比、O质量分数、惰质组含量、C质量分数、Rmax、镜质组含量。

此外，T检验对应各自变量的P均超过0.05，说明单自变量对煤转化率均没有显著影响[31-32]。同时，除X12外，其他自变量的VIF均超过10，说明各个自变量间存在较强的多重共线性[33-34]，从而导致多元线性回归拟合模型的可靠性较差。

对逐步回归模型Z2和Z3进行F检验，结果表明：其F分别为11.506和9.005，而其F0.05分别为4.301和3.467，F>Fα；其P分别为0.003和0.001，均小于0.01。因此，模型Z2和Z3得到的回归方程均有统计学意义。由模型Z2和Z3自变量的T检验可知：其P<0.05，说明各自变量的影响是显著的；其VIF<10，说明各自变量之间已不存在多重共线性。而与模型Z2相比，模型Z3的逐步回归方程拟合度更高，相关系数R为0.679。其拟合精度虽不如多元线性回归模型，但因消除了自变量的多重共线性，结果可靠性更高。其回归方程为：

Y1=97.738-0.103X11-4.679X12

(2)

由模型3可以看出，煤转化率与惰质组含量、Rmax成负相关，且惰质组含量对应Beta的绝对值大于Rmax的，说明惰质组含量对转化率的影响高于Rmax。这与文献[24]研究结果一致。Rmax是反映煤变质程度的重要指标，一般随煤变质程度的加深而增加[35]。因此，对煤液化而言，煤变质程度越低，Rmax越小，越利于液化。

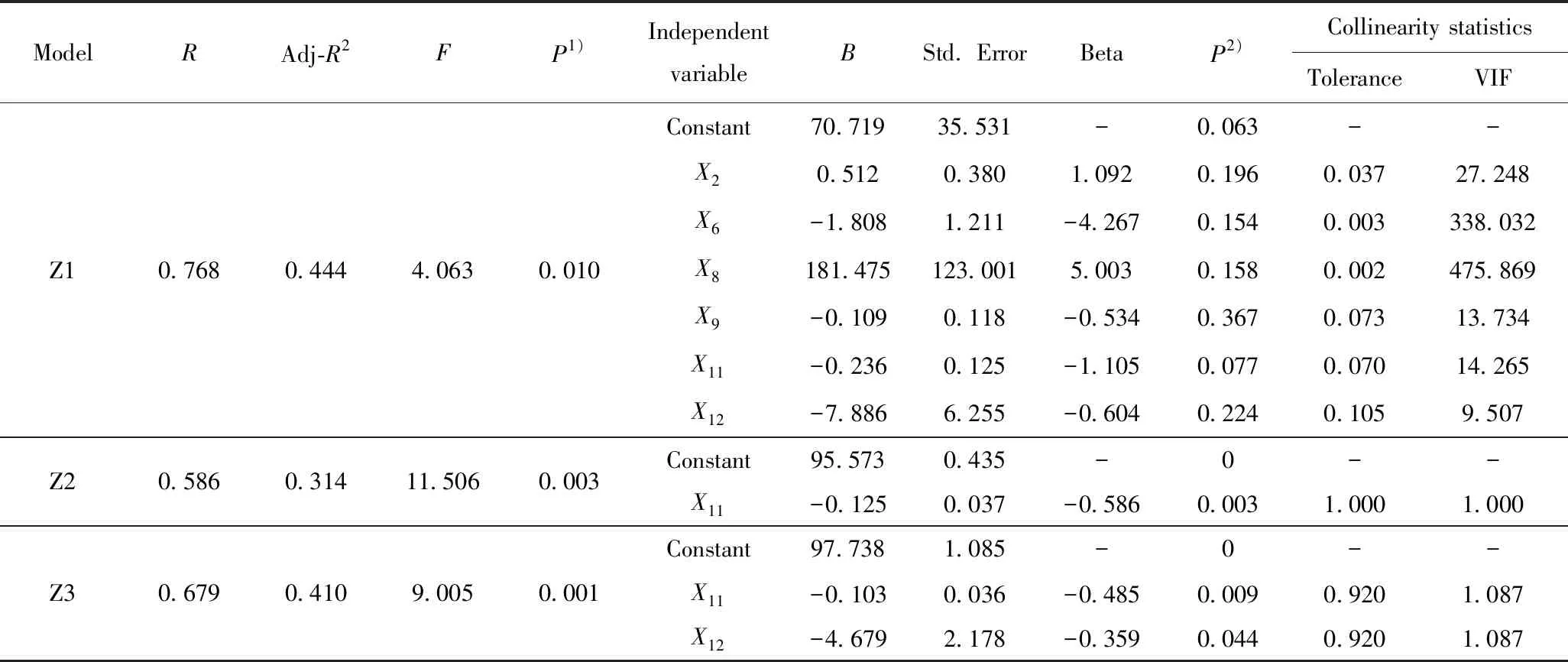
表2 煤质特性与转化率回归模型的方差分析和回归系数Table 2 Variance analysis and regression coefficients of coal characteristics and conversion rates

1.2 煤质特性与水产率回归分析

为了避免自变量间的多重共线性，以Y3为因变量，X1、X2、X3、X6、X8、X9、X11、X12为自变量，直接进行逐步回归分析，结果见表3。由表3可以看出，Y3仅受X8的影响，其回归方程为：

Y3=5.736+53.472X8

(3)

表3 煤质特性与水产率回归模型的方差分析和回归系数Table 3 Variance analysis and regression coefficients of coal characteristics and water yields

该模型的相关系数R为0.906，修正决定系数Adj-R2为0.813，说明逐步回归模型线性拟合效果很好。文献[36]研究发现，在煤液化过程中，煤中77.83%(质量分数，下同)的氧元素会与氢气反应生成水，11.58%的氧会生成COx，10.73%的氧会留在液化油及残渣中。因此，若O/C原子比增加，预示着煤的变质程度较低，更易液化。因此，液化油及残渣中留存的氧可能会进一步转化变成水及COx；同时由于C含量的降低，可能会减少COx的生成，从而提高水产率。

1.3 煤质特性与气产率回归分析

以Y4为因变量，X1、X2、X5、X6、X8、X9、X11、X12为自变量进行逐步回归分析，得到3个逐步回归分析模型(Q1、Q2、Q3)，结果见表4。由表4可知，与模型Q1和Q2相比，模型Q3的逐步回归方程相关系数为0.825，拟合程度最高。其回归方程为：

Y4=-33.379+0.535X6+0.089X9+0.429X2

(4)

因此，煤液化的气产率与C、O元素含量和镜质组含量呈正相关。其中，O元素含量对气产率的影响最大，C元素含量次之，镜质组含量影响最小。这是因为O含量越高，煤的变质程度越低；镜质组含量越高，越易液化生成液化油和气体。文献[36]研究表明，煤中的C元素约有12%(质量分数)会进入气体中，因此，C元素含量的升高可能会提高气体产率。

表4 煤质特性与气产率的方差分析和回归系数Table 4 Variance analysis and regression coefficients of coal characteristics and gas yields

1.4 煤质特性与沥青质产率回归分析

以Y5为因变量，X1、X2、X6、X7、X8、X12为自变量进行逐步回归分析，得到2个逐步回归分析模型(L1、L2)，结果见表5。与模型L1相比，模型L2的逐步回归方程拟合程度更高，相关系数R为0.720，为较优模型，其回归方程为：

Y5=14.453+12.062X12-16.783X7

(5)

Rmax越高，煤的变质程度越高，煤越难以液化，从而导致沥青质产量会增加；而H/C原子比越高，越易液化，沥青质产量也越低。由模型2可以看出，沥青质产率与Rmax呈正相关，与H/C原子比呈负相关，与理论分析是相符的，且Rmax对沥青质产率的影响高于H/C原子比。

表5 煤质特性与沥青质产率的方差分析和回归系数Table 5 Variance analysis and regression coefficients of coal characteristics and asphaltene yields

1.5 煤质特性与氢耗回归分析

以Y6为因变量，X2、X4、X6、X8、X9、X12为自变量进行逐步回归分析，得到2个模型(H1、H2)，结果见表6。与模型H1相比，模型H2的逐步回归方程拟合程度最高，相关系数R为0.690，为较优模型，其回归方程为：

Y6=3.800+0.756X4+0.053X6

(6)

由式(6)可以看出，氢耗与煤中的N、O元素含量呈正相关，且N含量的影响要高于O含量的。文献[36]研究表明，煤中的N元素和O元素经过液化反应后，有50%(质量分数)的N元素会与氢反应生成氨，有77.83%的O元素会与氢反应生成水。因此，当煤中N、O元素含量较高，会导致氢耗增加。至于N含量对氢耗的影响高于O含量的原因，目前还未有合理解释，仍需进一步深入研究，推测可能是因样本数偏少导致的。

表6 煤质特性与氢耗方差分析和多元线性回归系数Table 6 Variance analysis and multiple linear regression coefficients of coal characteristics and hydrogen consumption

1.6 煤质特性与油产率关系

前文通过SPSS 22.0软件分析煤质特性与油产率相关性发现，Y2只与X3显著相关。对其进行逐步线性回归可得关系方程：

Y2=45.150+3.633X3

(7)

方程(7)的相关系数R为0.476，决定系数R2为0.227，修正决定系数Adj-R2为0.192，拟合程度较低。在煤炭直接液化试验中，油产率是多个煤质特性综合作用的结果，除了受X3影响外，还可能受X1、X2、X11、X12等因素影响，只是影响可能不显著。因此，为了更好地反映油产率与煤质特性的关系，采用差减公式：Y2=Y1+Y6-Y3-Y4-Y5，可间接得到油产率与煤质特性的关系。经过计算，其拟合方程为：

Y2=114.728-0.429X2+0.756X4-
0.482X6+16.783X7-53.472X8-
0.089X9-0.103X11-16.741X12

(8)

2 回归模型预测效果

2.1 煤种预测值与实验值的对比分析

为判断回归模型的预测效果，将回归分析预测值与液化试验值进行对比，选择二者的标准误差(Std. Error)、平均相对误差(M.R.Error)、平均绝对误差(Re.Error)作为评价指标[37]，结果见图1和表7。由图1和表7可知：回归分析的转化率预测值与试验值的标准误差、平均相对误差、平均绝对误差均较小，说明回归模型对转化率的预测效果较好；由回归分析得到和由差减公式计算得到的油产率预测值与试验值的标准误差、平均相对误差和平均绝对误差相近，均不超过3.50%，且后者的三项误差更小。这说明通过差减公式计算得到的油产率与试验值吻合度好于回归分析，也证实了油产率不仅受氢元素含量的影响，而且受多个煤质特性综合影响。

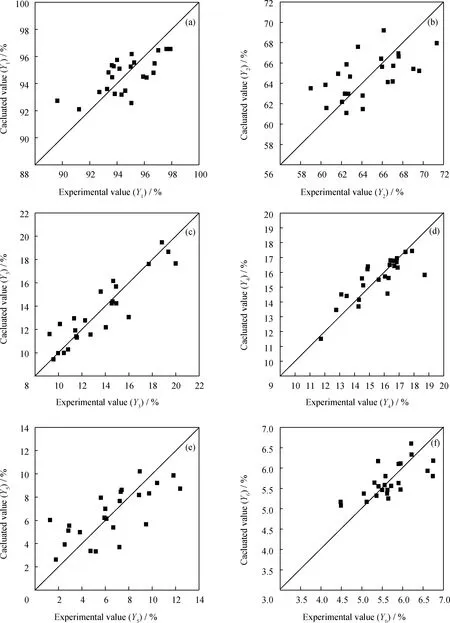
图1 回归分析结果与试验结果对比Fig.1 Comparison of regression analysis results with experimental results(a) Conversion; (b) Oil yield; (c) Water yield; (d) Gas yield; (e) Asphaltene yield; (f) Hydrogen consumption

回归分析得到的水产率、气产率、氢耗的预测值与试验值的标准误差和平均绝对误差很小，均不超过1.0%，但二者的平均相对误差都较高，在4.4%～7.6%之间。回归分析得到的沥青质产率预测值与试验值的标准误差和平均绝对误差较低，而平均相对误差很大，为43.39%。这是由煤液化产物的选择性不同及物料平衡波动共同作用造成的。在煤液化过程中，为了提高油品收率，在保证煤转化率较高的同时，必须抑制水、气、沥青质的生成，尽可能多地得到油品，且减少氢气的消耗。因此，在煤液化过程中，水、气、沥青质、氢气的生成或消耗数值较小。煤液化过程的油产率一般在60%以上，而沥青质产率为1.28%～12.39%。当物料平衡的波动为±2%时，若该波动全由沥青质产率波动造成，则沥青质产率的相对误差为16.14%～156.25%；若该波动全由油产率波动造成，则油产率的相对误差不超过3.33%。可见，同等物料平衡波动下，沥青质产率的相对误差明显高于油产率的，因而沥青质产率的平均相对误差会比较明显。但实际水产率、气产率、沥青质产率及氢耗的标准误差和平均绝对误差均很小，均不超过2.09%，低于油产率的标准误差和平均绝对偏差，说明逐步回归预测的模型整体可靠性较好[38]。

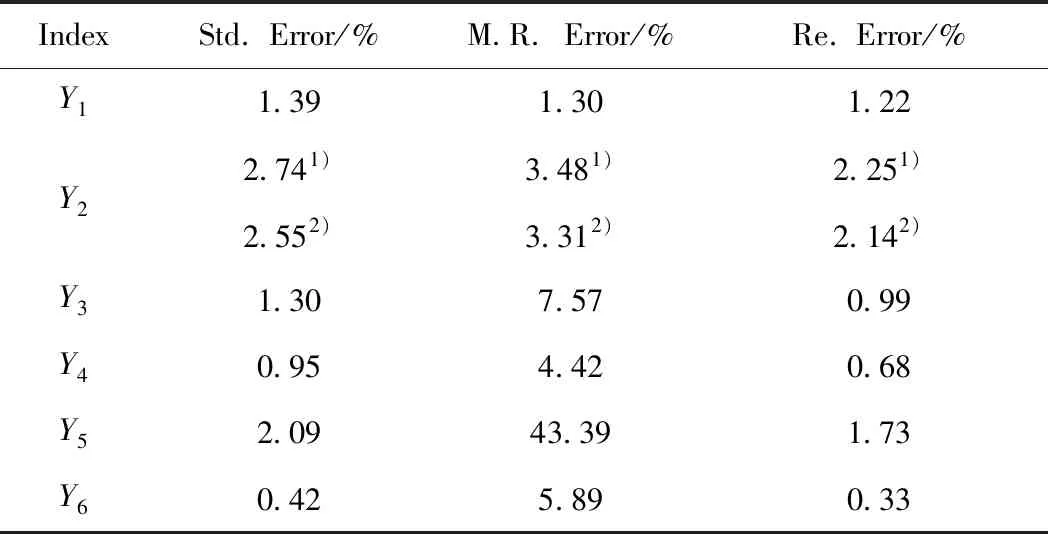
表7 试验值与预测值的误差分析Table 7 Error analysis of experimental value and calculated value

2.2 验证煤种预测值与试验值的对比分析

为了验证回归模型适用性，选择其他地方或者不同煤层的煤种作为验证煤种，对其模型预测值与试验值进行对比，结果如表8所示。由表8可知：验证煤种的转化率预测值与试验值的标准误差、平均相对误差、平均绝对误差均低于2.10%；差减法得到的油产率预测值与试验值的标准误差、平均相对误差和平均绝对误差均低于2.25%；预测值与试验值吻合度较高，说明模型也可以用于其他液化煤种的评价与筛选。

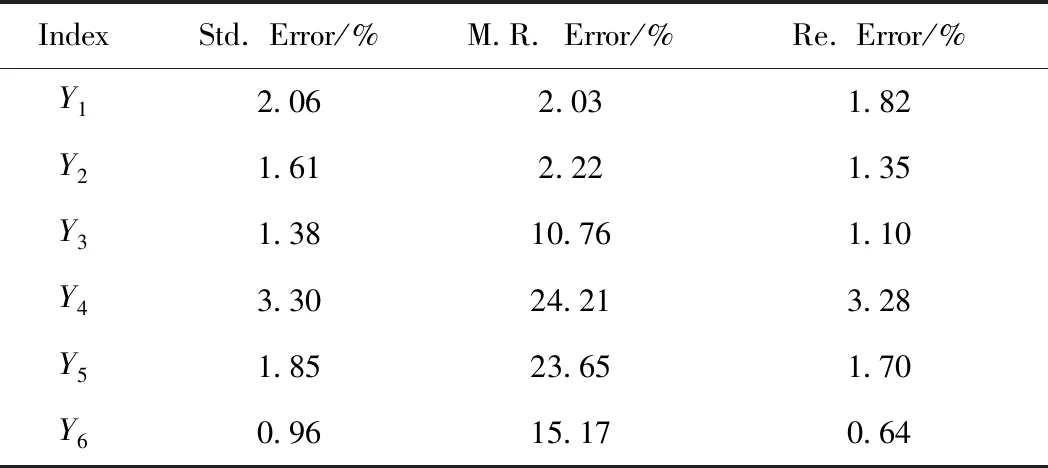
表8 验证煤种试验值与预测值的误差分析Table 8 Error analysis of other coals experimental value and calculated value

从平均相对误差角度来看，回归模型对验证煤种水产率、气产率、氢耗的预测值与试验值的误差较大，预测的可靠性较差。但从标准误差和平均绝对误差角度来看，以上4项参数二者的数值都很小，逐步回归预测的模型可靠性较好。

3 结 论

(1)煤质特性及其液化特性的相关性分析发现，液化特性与多种煤质特性相关性显著。除油产率外，煤转化率、水产率、气产率、沥青质产率和氢耗均受C和O元素含量、O/C原子比、Rmax等4种煤质特性的影响，其中，煤转化率、水产率、气产率、氢耗与C元素含量、Rmax成负相关，与O元素含量、O/C原子比成正相关；而沥青质产率与C元素含量、Rmax成正相关。

(2)通过多元线性回归分析与逐步回归分析发现，液化特性不同，受煤质特性的影响也不同。如转化率主要受惰质组含量和Rmax的影响，其中惰质组含量对转化率的影响要高于Rmax；沥青质产率主要受H/C原子比和Rmax的影响，其中Rmax对沥青质产率的影响要高于H/C原子比。

(3)对比模型预测值与液化试验值发现，预测值与试验值的标准误差不超过3.30%，平均绝对误差不超过3.28%，完全可以用于初步评价和筛选适合液化的煤种。