基于响应曲面法的双切向环流式气体分布器优化设计

（西南石油大学，四川 成都 610500）

填料塔是天然气预处理工艺的核心设备之一，其运行效果对天然气处理能力、处理品质以及整体经济效益具有重大意义。气体是否在填料塔内均匀分布关系到填料层的利用效率以及气体品质［1-2］。填料塔气体分布器对于入口来流的均布至关重要，其性能好坏直接影响填料塔的运行效果。结构设计合理的气体分布器应能使塔内预处理气流在垂直于流向的截面上均匀分布，同时压力损失还要尽可能的小，减少能耗。

目前，工业应用较多的气体分布器主要有双锥导流式、双列叶片式及双切向环流式等［3-6］。其中，双切向环流式气体分布器应用效果好，相关学者和技术人员对其进行的研究也较多。刘德新等［7］利用计算流体动力学（CFD）方法建立双切向环流式气体分布器内三维气液两相模型，讨论了导流叶片数量、导流板径向夹角对分布器性能的影响。岳明［8］以变压吸附塔的进口气体分布器为研究对象，分析了运行工况、分布器结构、安装位置等因素对分布器性能的影响并提出优化参数范围。金新民［9］建立了FLNG填料塔进口气体分布器数值模型和在晃动工况下气体分布器试验装置，研究了海上晃动工况对气体分布器性能的影响，得到了晃动工况对气体分布器性能的影响规律。李雪［10］针对大型火电厂CO2吸收塔的设计，采用CFD方法，研究了大直径新型规整填料塔气体分布器的结构优化问题。洪都等［11］提出了一种双层多环大孔径气液同轴喷射分布器，进行了单喷嘴冷模试验和数值仿真论证，认为新结构能实现进料气液均布，而且其性能受负荷波动影响小。

文中应用模拟软件FLUENT建立双切向环流式气体分布器数值模型，分析结构和运行参数对其性能的影响，以期总结出最优分布器设计参数，为工程项目的设计提供指导。

1 气体分布器结构及模型

1.1 分布器结构

双切向环流式气体分布器结构示意图见图1,其主要结构组件为分流板、导流叶片、环形顶板以及内筒。环形顶板紧贴罐体内壁面，在内筒、顶板以及罐体内壁面之间形成环形通道，导流叶片位于环形通道内并紧贴内筒及罐体内壁面。从进口流入分布器的气流被分流板一分为二，从其两侧进入环形通道，均匀分布的导流叶片将环形通道内的气流导入填料塔塔底，气流由塔底向上流动并由分布器出口流出。

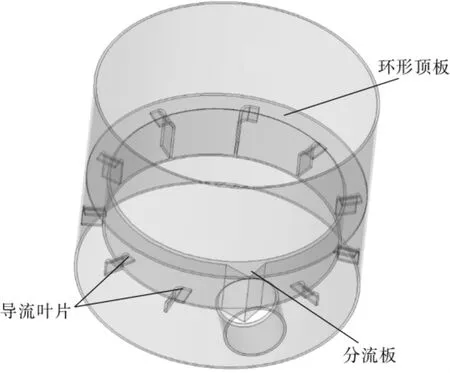
图1 双切向环流式气体分布器结构示图

1.2 分布器结构参数

双切向环流式气体分布器结构几何尺寸参数见表1［9］。为便于对数值模型的准确性进行验证，以此模型为分析设计的基准模型。

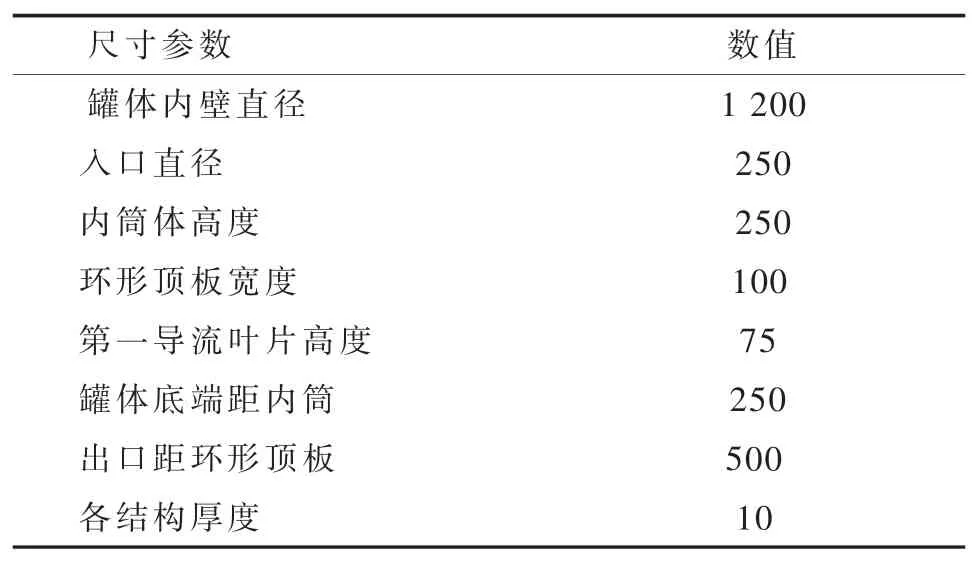
表1 分布器基准模型尺寸 mm

1.3 分布器网格划分

双切向环流式气体分布器分析设计的基准模型及网格划分见图2。考虑到分布器结构不规则，采用非结构化多面体网格对流场区域进行离散，并对近壁面区域进行网格加密。

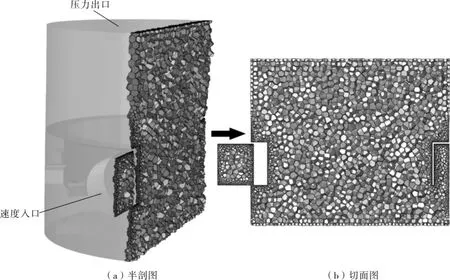
图2 双切向环流式分布器分析设计基准模型及网格划分

1.4 分布器性能评价指标

气体分布器的评价指标包括压力损失p和出口端气体分布不均度M。p为气流进、出口压差，p越小，分布器性能越好。

气体分布不均度M是衡量分布器出口端面速度均一度的常用评价指标。M越小，表示速度的分布越均匀，M的计算公式为：

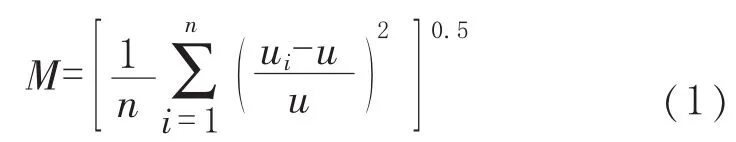
式中，n为分布器出口端平面取点个数；ui为第i个出口测点的气体流速，u为所用测点平均气体流速，m/s。

1.5 网格无关性验证

为了在节省计算资源的同时避免求解出现离散误差，保证结果的准确性，对网格进行无关性验证。验证过程中使用的网格序号及其对应的网格数量、计算的压降及压降误差、不均度及不均度误差见表2。

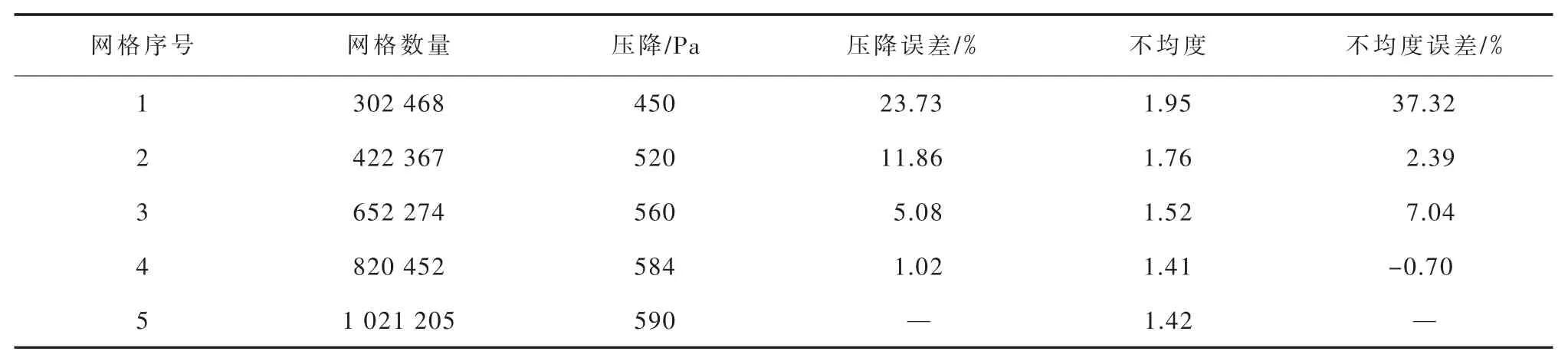
表2 分布器网格无关性验证

分布器网格无关性验证结果见图3。从图3可以看出，当网格数量增长至820 000之后，进一步增加网格数量，求解结果无显著变化，对比求解误差较小。因此，文中数值计算模型统一采用第4种网格尺度。

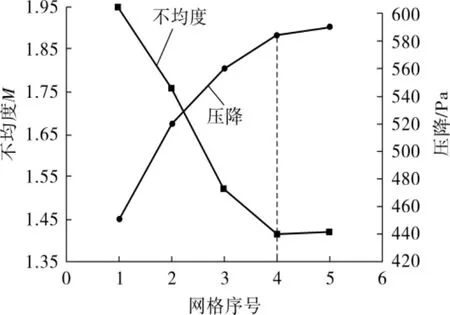
图3 分布器网格无关性验证

1.6 FLUENT求解设置及模型准确性验证

文中采用FLUENT作为模型求解器，紊流模型选择Realizable κ-ε模型，压力与速度解耦采用SIMPLE算法，质量、动量和能量控制方程均采用二阶格式，计算收敛条件为残差值小于10-4。模拟使用的介质为空气，考虑为不可压缩理想气体，忽略重力，操作压力为常压，分别设置速度入口和压力出口，其余边界均为壁面无滑移边界条件。以文献［9］中的试验和数值仿真结果为参照，验证文中数值仿真计算模型的准确性，结果见图4。从图4可以看出，本文的数值计算结果与参照曲线的总体规律基本一致，据此判定本文数值计算方法和结果准确可靠。

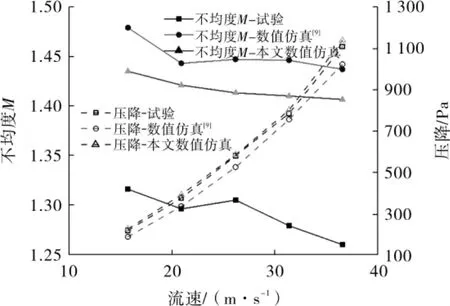
图4 分布器模型准确性验证

2 气体分布器优化设计

2.1 优化方法

采用响应曲面分析法 （response surface methodology,RSM）进行气体分布器的优化设计。RSM是通过对回归方法的分析、优化工艺参数预测响应值的一种统计方法，该方法可以反映出不同因素对试验结果的交互影响，弥补普通正交优化方法仅考虑单因素对试验结果的影响的不足，在分析研究中应用广泛［12-15］。

2.2 数值模拟及显著性分析

2.2.1 正交试验方案及模拟结果

以压力损失和不均度为响应值，以影响分布器性能的3个因素，即第一导流叶片高度A、导流叶片数量B及入口流速C为考察因素，建立Box-Behnken试验因素与水平正交表，见表3。试验结果与分析见表4。其中，导流叶片高度按等差均布。

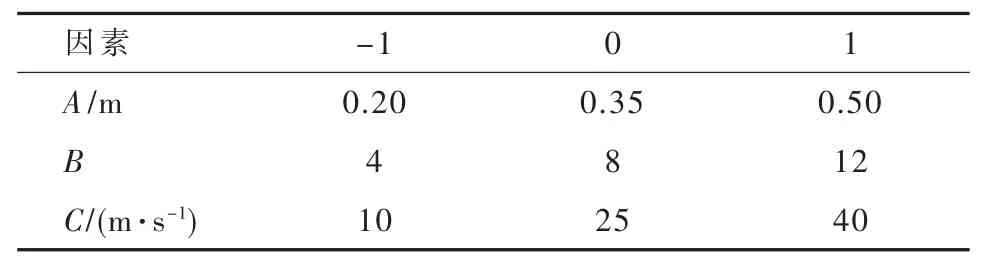
表3 正交试验因素与水平

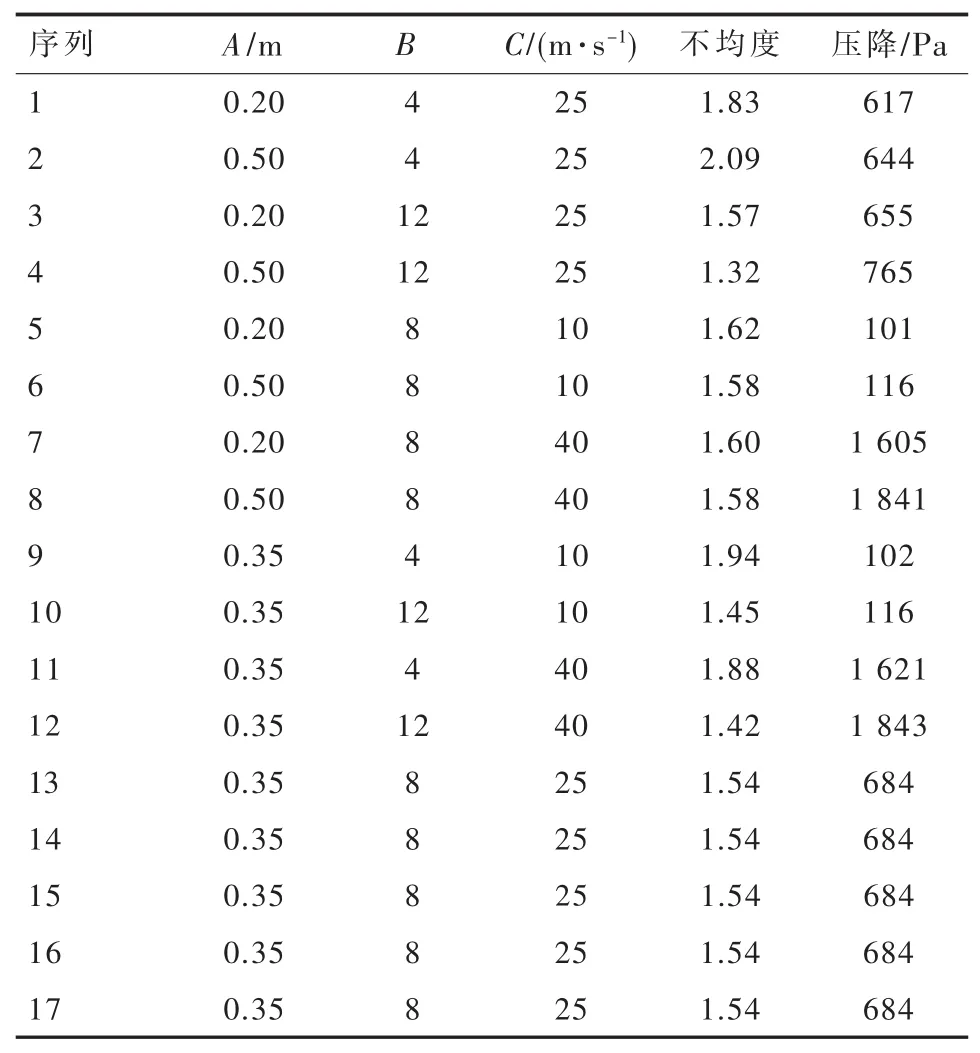
表4 响应曲面正交试验结果

2.2.2 响应面试验数据拟合

拟合压降和不均度数据，得回归方程：

以不均度为例对回归方程进行方差分析，所得多元回归模型方差分析结果见表5，选择因素模型综合参数如下：标准偏差0.015、均质1.62、变异系数0.93%、预测模型的残差平方和0.026、R2=0.997 4、R2调整值为 0.994 1、R2预测值为0.959、精确度 64.53。

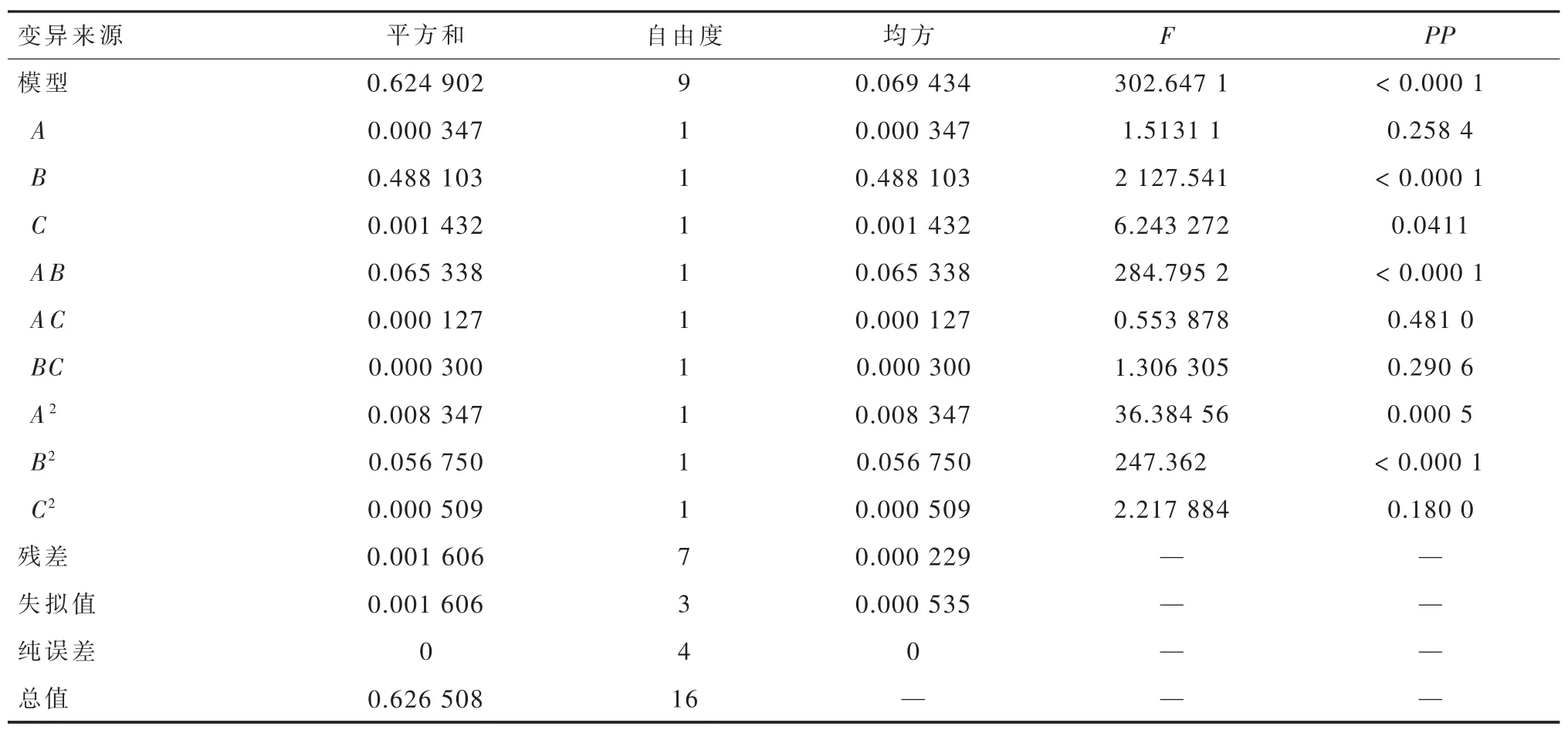
表5 不均度多元模型回归分析

表5中，F值是方差分析中的一个重要指标，含义为回归模型的试验方差，PP为衡量控制组和试验组差异大小的指标,其中F值越大、PP值越小，表明分析结果越可靠，例如PP等于0.001，表示99.9%的概率认为结论是正确的。通过F值可知，试验中各因素对不均度的影响大小顺序是B、C、A；对压降的影响顺序是 C、B、A。

选择因素模型的 R2为 0.997 4，R2调整值为0.994 1，R2预测值为0.959，三者数值相差很小，说明此模型合理，能够较好地解释试验数据。精确度是度量干扰系数的标志，一般精度大于4是合理的，本模型中精确度为64.53，说明所用模型与试验拟合契合度较好，证明建立的数学回归模型可靠。

为了考虑各观测数据相对于回归拟合是否为异常点，通过作图对压降和不均匀度的实际值与预测值进行对比，结果见图5和图6，图中散点代表预测值，实线代表实际值。由图5、图6可知，数据点基本分布在直线或直线两侧，模型的拟合效果较好。

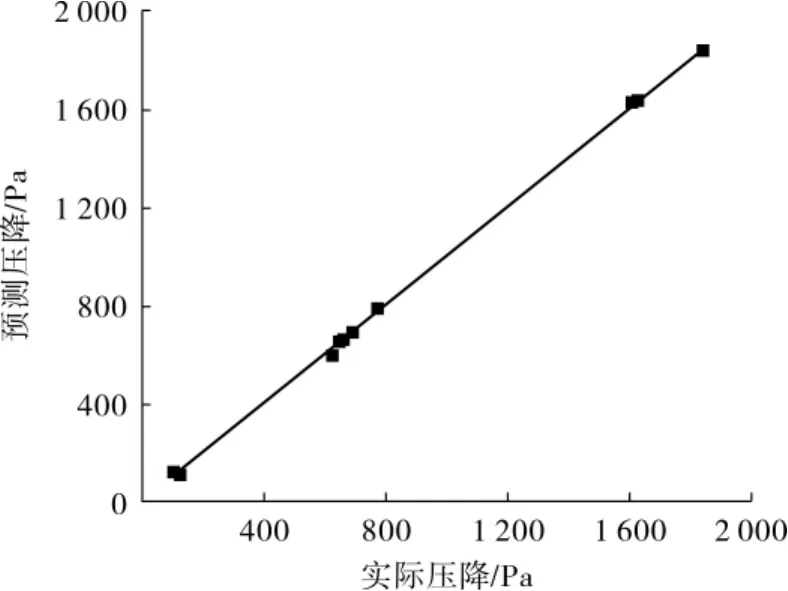
图5 分布器压降预测值与实际值关系

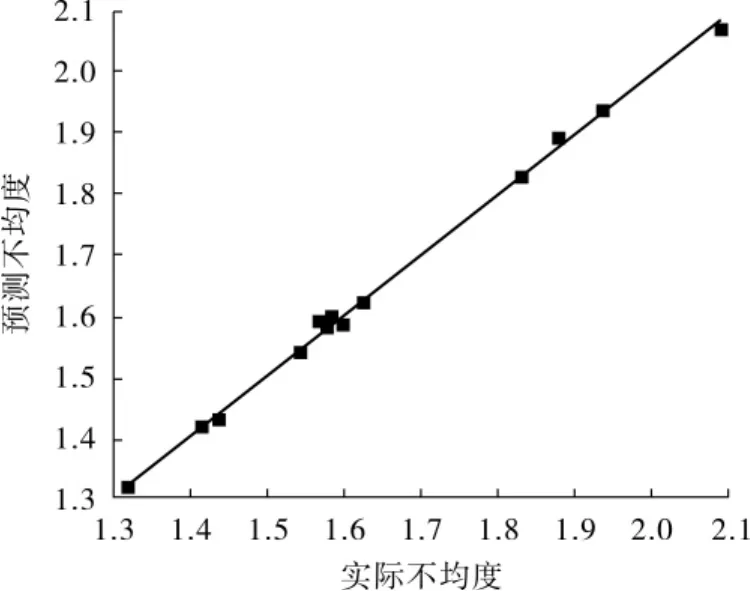
图6 分布器不均度预测值与实际值关系

2.2.3 响应面分析

参数A、B、C交互作用对压降和不均度的响应曲面见图7～图10。

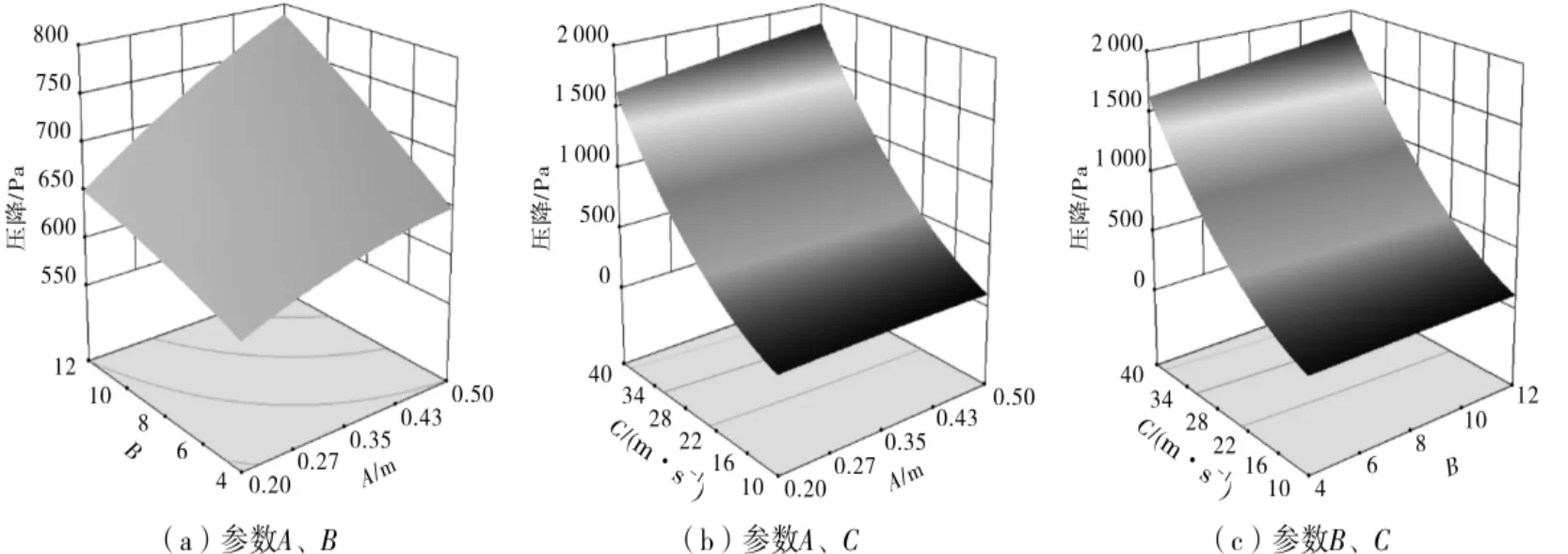
图7 参数A、B、C对分布器压降的交互影响曲面图

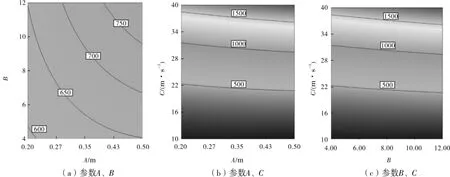
图8 参数A、B、C对分布器压降的交互影响等值线图

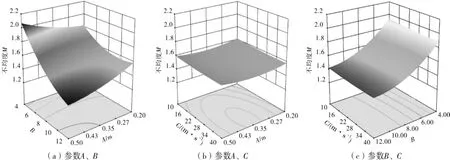
图9 参数A、B、C对分布器不均度M的交互影响曲面图

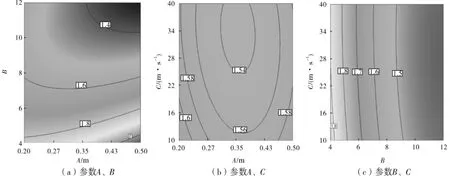
图10 参数A、B、C对分布器不均度M的交互影响等值线图

由图7和图8可知，分布器压力损失随着参数A、B、C的增大而增大。当导流叶片高度增大时，气流与叶片的接触面积增大，气流与叶片间产生的冲击力也较大，导致分布器压力损失增加。同理，导流叶片数量增加也会导致气流扰动增大，摩阻增大。

由图9和图10可知，参数A、B交互作用明显，参数A、C与B、C之间交互作用较小。参数C恒定，当导流叶片数量小于6时，随着导流叶片数量的增加，速度不均度呈增长趋势；反之，速度不均度呈下降趋势。其原因在于，当导流叶片数量较少，第一导流叶片高度较大时，会导致分布器出口端前端气流聚集，不利于气流在出口端的均布。

根据所得回归方程，计算不同流速下多孔板最优结构参数，得到的不同入口速度下分布器最优结构参数见图11。由图11可知，随着流速的逐渐增大，最优结构参数B在7～12呈逐渐减小趋势，结构参数A在0.455～0.225 m且呈逐渐减小趋势。

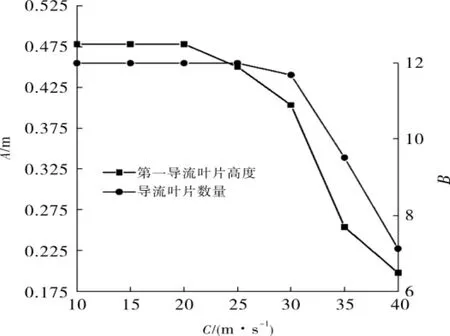
图11 不同入口速度下分布器最优结构参数

3 结语

以压力损失和气体速度不均度为评价指标，通过CFD方法建立了双切向环流式气体分布器数值模型，利用响应曲面法研究了不同结构参数与工况条件的交互作用对分布器性能的影响，得到了不同流速下分布器最优结构参数，具有工程指导意义。研究结果表明，当参数C恒定，导流叶片数量小于6时，随着导流叶片数量的增加，速度不均度呈增长趋势；反之，速度不均度呈下降趋势。根据响应曲面法，试验中各因素对不均度的影响从大到小排序为B、C、A，对压降的影响从大到小排序为C、B、A。随着流速的增加，最优结构参数B在7～12逐渐减小，结构参数 A在0.455～0.225 m逐渐减小。