一种雷达侦察宽带信号接收的方法

蔡 凡

(闽南理工学院电子与电气工程学院，福建 泉州 362700)

0 引言

近年来，数字信道化技术[1]已成为软件无线电思想的关键技术之一，也是雷达侦察接收机的主流技术体制，在新体制雷达中，线性调频(LFM)信号[2]是一种大时宽带宽积信号，易产生、对多普勒不敏感等特性，在雷达、声呐以及通信系统中被广泛应用。传统的傅里叶域信道化接收机随着傅里叶频域信道的细致划分，宽带线性调频信号的能量会溢出到多个信道里面，加大了后续信号处理的难度。

分数阶数字信道化接收机是基于分数阶傅里叶变换(FRFT)对线性调频等非平稳信号的聚焦性能[3]，将宽带LFM信号聚焦在一个分数域信道内输出，从而解决了传统信道化接收机在接收宽带信号时的跨信道问题。然而由于低通滤波器的非理想特性，即实际工程中的滤波器具有一定的过渡带，这给分数阶信道化接收机带来了一些新的问题。由于分数阶信道化接收机需要预先估计求出线性调频信号的调频率来构建分数阶信道化结构，当调频率估计得不准确，即宽带线性调频信号不能够完全聚焦时，就会形成一个具有一定带宽的信号，当这个信号落在滤波器的过渡带上时，就会出现跨信道的问题[4]；即使调频率估计得完全精确，即接收到的宽带线性调频信号完全聚焦，但当聚焦后的信号落在滤波器的过渡带上时，会在相邻的信道内有输出[5]，信道检测会输出一个虚假信号，这对后续的信号处理带来了一定的复杂度。本文主要针对雷达侦察宽带信号提出一种基于奇偶分数阶交替信道化新体制的宽带数字接收机的方法。

1 分数域奇偶信道化理论模型

对于宽带LFM信号分数域奇偶交替信道化的接收方法，首先根据观测宽带信号的特征，选定与信号匹配的分数阶傅里叶变换的旋转角度α=acot(μ)，μ是信号估计的调频率(μ的估计已有成形方法，例如利用传统傅里叶信道化接收，然后对信道输出利用瞬时自相关算法得到调频率μ的估计值)[6]，信道数为K，抽取因子为M，并且K=MF，F为正整数(F通常取2)，在将时域变换成频域分析过程中，采用快速傅里叶变换算法基2-FFT，故信道数K一般是2的幂次方，一般K的取值为8、16或32适宜。这是因为信道数K越多时，信号的分辨率越高，但随着输入信号的带宽增大，信号能量会被分裂到多个信道内，导致信号能量的泄露和资源消耗较多：信道数较少时，中心频率过低，信号的分辨率会降低，且处理速率需要较高，不易进行实时处理。基于折中考虑，本文信道数采用K=16，8倍抽取的数字信道化接收进行实验分析。

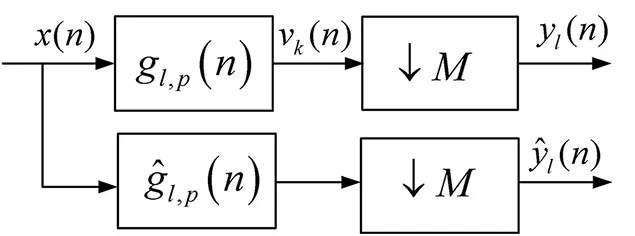
图1 第l通道奇偶信道化接收理论模型Fig.1 Theoretical model of odd and even channelized reception for channel l

根据分数阶傅里叶(Fourie)变换对非平稳信号的能量聚焦特性[7]，分数阶Fourie域M通道信道化[8]可以采用分数阶Fourie域滤波器替代传统Fourie域信道化中对应的滤波器。由分数阶傅里叶域滤波器与傅里叶域滤波器的关系，将构造的两种傅里叶域滤波器组转换成分数域滤波器组。因此p阶分数阶Fourie域第l条支路的结构如图1所示。

输入信号与两种分数域滤波器做P阶分数阶卷积，进行交替滤波，输出最终信号。其中，偶型信道输出

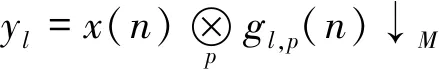
(1)

奇型信道输出

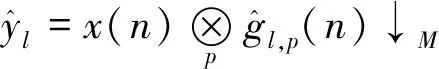
(2)

其中，l=0,1,2,3,…,K-1，根据傅里叶域滤波器与分数域滤波器的关系可得

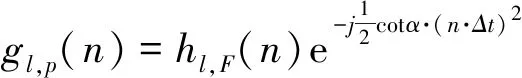
(3)

(4)

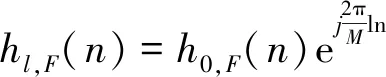
(5)

(6)

2 奇偶型滤波器组

基于多相滤波结构的分数阶信道化可大大降低数字信道化的实现结构，分数阶傅里叶变换(FRFT)可以解释为信号在时频平面上的旋转算子[9]，对线性调频等非平稳信号具有良好的能量聚焦性。其中奇型滤波器组和偶型滤波器组排列方式分别如图2所示[10]。

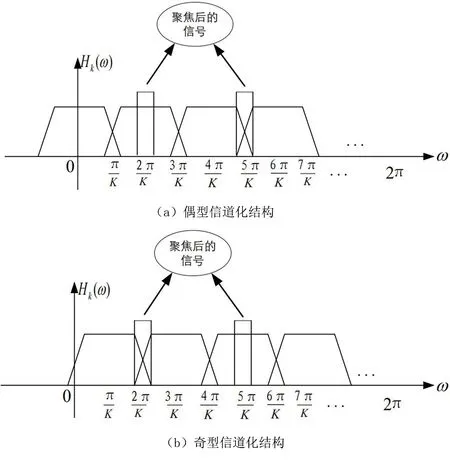
图2 两种信道化分结构Fig.2 Two channelization sub structures

其中，K为信道数。第k路的中心频率为ωk，偶型滤波器组中第k个带通滤波器的中心频率ωk=2πk/K，而奇型滤波器组中第k个带通滤波器的中心频率ωk=2π(k+1/2)/K。由图2可知，位于偶型滤波器组过渡带的信号一定位于奇型滤波器组的通带上，而位于奇型滤波器组过渡带的信号一定位于偶型滤波器组的通带上。这样利用两种形式滤波器组之间的互补关系，可以保证聚焦后的信号落在滤波器的通带上，从而解决虚假信号和跨信道的问题。

3 分数阶信道化高效实现结构

针对传统的数字信道化结构对每一路信号都要提供不同的调制因子，运算量大，不易实时实现。分数阶傅里叶域多抽样信号处理和分数阶傅里叶域滤波的发展及多相滤波结构的分数阶信道化的相关原理，促成了分数阶信道化高效实现结构的推导。首先利用传统卷积代替分数阶卷积，式(2)可转化为：

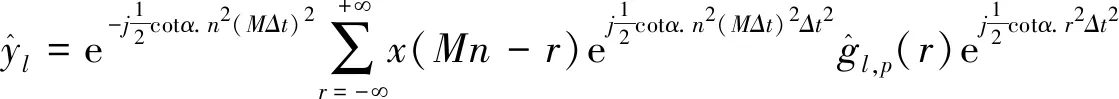
(7)

其中，设r=Km+l,l=0,1,2,…,K-1，xl(n)=x(Mn-l)，代入式(7)得：

(8)

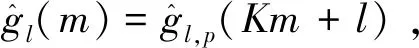
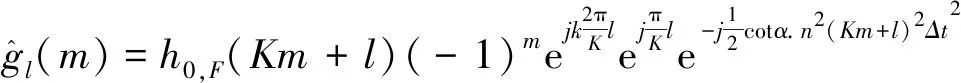
(9)

将式(9)代入式(8)可得：

其中，hl(m)=h0,F(Km+l)。将奇型信道化与偶型信道化进行融合后得到的输出表达式为

(10)

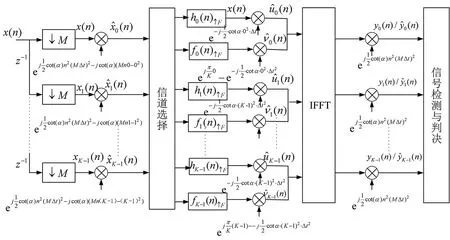
图3 分数域奇偶交替信道化的系统结构图Fig.3 System structure of odd and even alternating channelization in fractional domain

通过上述高效结构，与偶型信道融合，进行奇偶交替滤波，使其在运算复杂度与分数域信道化接收相当情况下，提高了后续参数测量的精度。同时说明了输出信号经过信号检测与判决时，输出结果为：如果在奇信道情况下，有两个信道有输出信号，说明信号没有准确聚焦，发生了跨信道现象，则关闭奇信道，打开偶型信道；若此时只有一个信道有输出信号，则直接输出。通过动态切换实现了输出信号的完整性。

4 奇偶分数阶信道化接收机

若只采用单一形式(奇型或偶型)的滤波器组来进行分数阶信道化，那么不可避免地会遇到虚假信号或者是跨信道的问题。而如果利用奇型滤波器和偶型滤波器之间的互补关系，可以使得宽带线性调频信号聚焦后落在滤波器过渡带的通带上，保存了信号信息的完整性，提高了信号参数估计的精确度。

4.1 奇偶分数阶信道化接收机流程

根据信道化高效结构中前两级复数调制合并后的调制因子，两种形式的分数阶信道化结构不同部分为滤波器系数和滤波后的复数调制因子，合并后的奇偶分数阶信道化结构将两种形式分数阶信道化的相同部分共用，不同部分分为两条支路，不仅完整保留了两种形式分数阶信道化的功能，而且实现了资源共用，降低了资源消耗，减小了系统的复杂度，达到满足雷达侦察设备更轻捷化的要求。奇偶分数阶交替信道化接收机串行结构流程如图4所示。

图4 奇偶分数阶信道化接收机并行结构流程图Fig.4 Flow chart of parallel architecture of odd even fractional order channelized receiver

设定分数阶信道化接收机的初始状态为偶型分数阶信道化，根据信道检测的结果进行判决，如果只有1个信道检测到信号，那么仍然继续进行偶型分数阶信道化接收；如果有相邻的两个信道检测到信号，则转换到奇型分数阶信道化接收；脉冲源源不断而来，判决转换模块持续判决选择哪一种形式的分数阶信道化，以确保聚焦后的信号落在滤波器的通带上，保留信号的完整信息，有利于后续的信号参数估计。

4.2 奇偶分数阶信道化接收机的阶次选择

奇偶分数阶信道化结构的构建前提是需要知道构建阶次，对于线性调频率信号来说就是该信号的线性调频率。由于线性调频信号是一种时频单调的调制信号，故当信号分裂时并不会破坏信号的调制特性，即信号的调制参数——调频率不会因为信号的分裂而改变。对分裂的信号部分单独进行处理，可以得到信号的线性调频率这一参数。基于瞬时自相关谱的调频率估计是一种有效的方法。由于傅里叶变换对信号的聚集性以及噪声的抑制，通过对信号的瞬时自相关做傅里叶变换可以在较低的信噪比下获取信号的调频率信息。

5 MATLAB仿真与性能分析

5.1 实验仿真

设定分数域奇偶交替信道化和分数域信道化信道数均为K=16信道，抽取倍数M=8(K=FM，F=2)。前端AD采样率为500 MHz，输入信号为宽带LFM信号载频为93 MHz，调频率为1.5 MHz/μs，带宽为100 MHz，信噪比(SNR)为0 dB，其时频域分布如图5所示。

可见，输入信号经过传统傅里叶域信道化以后，产生了能量溢出，被分裂到了信道号为0，1，2，3的信道内；经过分数域信道化后，由于信号靠近滤波器的过渡带以及分数变换阶次的聚焦误差，使得信号被分裂到第0信道和第1信道内，如图6(a)所示；而经过分数域奇偶交替信道化时，首先打开分数域偶信道而经检测出信号分裂后，转换为分数域奇信道化，使信号能够聚焦到了第0信道，如图6(b)所示。

由以上仿真实验可以得到，利用分数域奇偶交替信道化的接受方法，能够实现任意载频的大带宽LFM信号的较完整接收。对非平稳信号具有很好的聚集作用，其性能优于传统信道化的接收和分数域信道化的接收。

5.2 性能分析

图7 输出信号起始频率估计相对误差曲线对比Fig.7 Comparison of relative error curves of initial frequency estimation of output signals

为了比较分数域奇偶交替信道化接收方法和分数域信道化接收方法的输出信号质量的完整性，分别对上述输入信号的起始频率估计相对误差、载频和脉宽的性能进行了对比，得到相应各个参数的曲线对比图形(图7)。

1)图7分别给出了两种方法对上述输入信号的起始频率估计相对误差，随输入信号信噪比变化的曲线。其中每个数据由1 000次蒙特卡洛仿真实验得到。

由图7可以发现，通过对输入信号经过两种形式的分数阶信道化后性能图比较，相比之下，由于分数域奇偶交替信道化接收方法能够灵活地进行信道切换，使得信号总能够准确聚焦到一个输出信道内，由于保留了信号信息的完整性，避免了信号的分裂，提高了输出信噪比。所以参数估计误差较低，有利于提高对信号参数测量的精度，在性能参数上，由于只是截取了信号的一部分，点数较少，会引入一些误差。

2)输入信号在每个信噪比下做200次蒙特卡洛仿真，得到测量载频和脉宽的性能曲线对比图(图8、图9)，通过对输入信号经过两种形式的分数阶信道化后测量载频和脉宽的性能图比较，可以知道当信号聚焦后落在滤波器的通带上时，由于保留了信号信息的完整性，有利于提高对信号参数测量的精度。

图8 载频的估计性能曲线对比图Fig.8 Comparison of estimated performance curve carrier frequency estimation

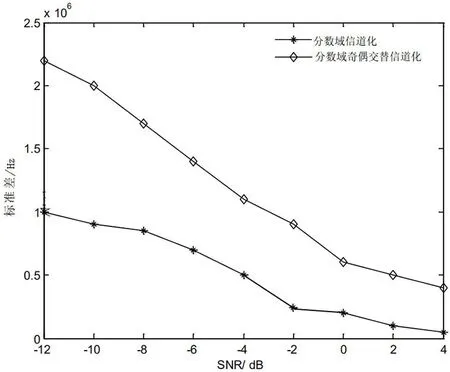
图9 脉宽的估计性能曲线对比Fig.9 Comparison of estimated performance curves of pulse width

6 结论

本文针对雷达侦察宽带信号的接收问题，以宽带LFM信号作为研究对象，研究了一种新体制的宽带数字接收机——奇偶分数阶交替信道化接收的方法。它作为分数阶信道化接收机的改进形式，利用分数阶域奇型滤波器和偶型滤波器之间的互补关系，可以保证信号落在滤波器的通带上，从而解决虚假信号和跨信道的问题。提出了奇偶分数阶信道化结构的工程实现模型，然后给出了奇偶分数域交替信道化接收机系统的流程图方案，可以很好地解决分数阶信道化接收机存在的问题，完善了分数阶信道化接收机系统。最后，通过MATLAB仿真试验，通过对分数域信道化和改进后的奇偶交替信道化的起始频率估计相对误差、载频和脉宽的性能分析和比较，验证了奇偶分数阶信道化接收机的有效性，为后续雷达监测信号提供有利的依据。