深海采矿钢结构塔架及底座平台的稳定性分析
余 倩,李文豪,杨高胜,陈丹东,谢梦琪
(1.中国舰船研究设计中心船舶工程部,湖北 武汉 430064;2.武汉船舶设计研究院有限公司系统工程部,湖北 武汉 430064)
自20世纪60年代以来,世界各国相继进行了深海矿产资源开采装备的研究,我国在“十三五”期间立项国家重点研发计划“深海多金属结核采矿试验工程”,该项目计划研制一套3 500m水深的深海采矿试验系统并完成不小于1 000m水深的海上整体联动试验。钢结构塔架及底座平台是水面支持系统的重要组成部分,其主体结构如图1所示。布放回收过程负载大、重复性高、作业速度快、易受波浪和风力影响,塔架和底座平台在承载和作业时可能发生结构不稳定的现象,因此,对整体结构稳定性进行分析具有重要的实际意义和理论价值。

图1 钢结构塔架及底座平台三维模型
文献[6]基于ANSYS对井架进行了线性屈曲和非线性屈曲分析,评估NDC-50DBT型石油钻机井架的整体稳定安全性能,结果表明相对于线性屈曲分析,非线性屈曲分析的屈曲因子为线性屈曲因子的0.33~0.72倍。文献[7]通过对JJ170/42-K型井架的静力分析、整体结构稳定性理论折算计算、线性屈曲分析和非线性屈曲分析,分别得出该井架的临界载荷,分析出发生危险工况的地方,提高其在使用过程中的安全性。文献[8]通过对双井架结构的静力分析、动力分析和稳定性分析,并与单井架的力学性能进行对比,得到双井架在静、动力载荷下的应力变化规律,找到薄弱环节并提出改进措施。
深海多金属结核采矿试验工程对钢结构塔架和底座平台的承载能力、刚度、强度和稳定性提出较高的要求。在工程中可以采用理论计算和计算机技术(有限元)相结合的方法对塔架和底座的整体结构稳定性进行分析和计算,为深海采矿的钢结构塔架和底座平台的结构设计和载荷选取提供技术借鉴和工程经验。
1 失稳问题分析
在立柱上施加沿柱轴线作用的集中载荷,当载荷达到屈曲载荷F
时,产生如图中虚线所示的弯曲变形,此时弹性荷载挠度曲线如图2(b)曲线a所示;随着载荷的增加,二阶弹塑性荷载挠度曲线为图中曲线c所示,此时立柱呈现极值点失稳现象,其极限载荷值为F
′;若形成机构破坏时,二阶刚塑性的曲线则为图2(b)中曲线b所示,其临界载荷为F
。
(a)单跨刚架 (b)荷载挠度曲线图2 失稳刚架的荷载挠度曲线
2 稳定性理论折算的计算
2.1 设计规范中的稳定性计算方法
参照GB50017-2003《钢结构设计规范》中第5章中的相关内容,在引入实腹式轴心受压构件的整体稳定性的基础上对压弯构件的稳定性问题进行分析和计算。
1)实腹式轴心受压构件的整体稳定性计算
实腹式轴心受压构件的整体稳定性计算公式为

(1)
式中:N
为构件的轴心力;φ
为轴心压杆的稳定性系数;A
为压杆的截面面积;σ
为稳定强度;f
为抗压强度设计值。2)压弯构件的稳定性计算
①弯矩作用在对称轴平面内(绕x
轴)的实腹式压弯构件稳定性应按下列公式计算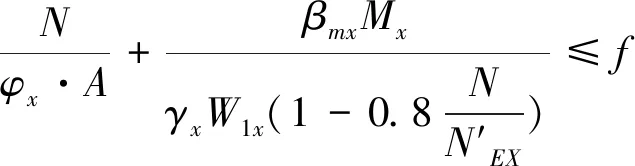
(2)

x
轴)作用的格构式压弯构件,其弯矩作用平面内的整体稳定性应按下式计算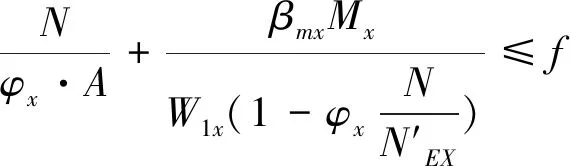
(3)
③弯矩作用在平面外的稳定性计算与实腹式构件相同,在此不再赘述。
④换算长细比
换算长细比按下列公式计算

(4)
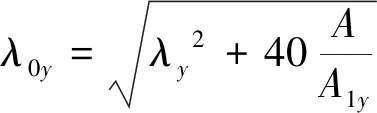
(5)
式中:A
1为构件截面中垂直于x
轴的各杆件毛截面面积之和;A
1为构件截面中垂直于y
轴的各杆件毛截面面积之和。综合以上分析和研究,对于压弯构件在分析其稳定性时需计算弯矩作用平面内和弯矩作用平面外两种情况,计算时需根据结构的最大弯矩、截面模量和相关系数等参数来确定。
2.2 稳定性理论折算的计算
钢结构塔架是由多个杆件组合成的桁架结构,底座平台是格构式压弯构件,综合考虑其结构特征和受力特点,采用整体稳定性计算方法,按实腹式压弯构件稳定性计算公式,进行塔架和底座平台的整体稳定性理论计算。
在塔架和底座平台上截取3个横截面进行分别计算,以最大值截面的计算结果为下一步有限元仿真分析的基础和依据。3个截面选取如图3所示。
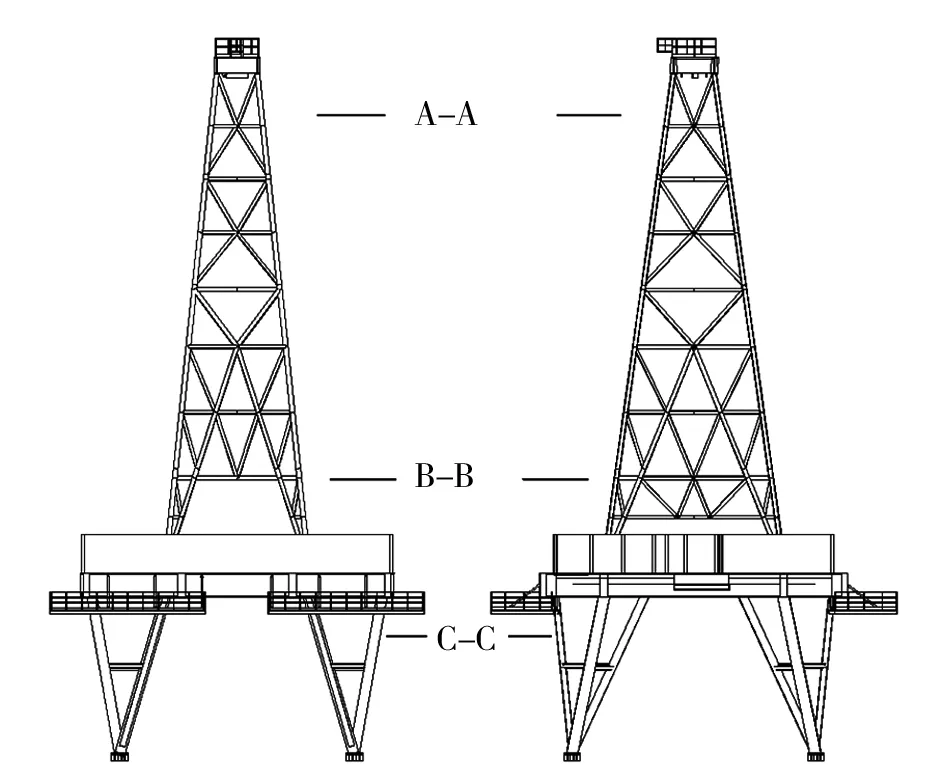
图3 稳定性理论折算的计算截面
1)A-A截面稳定性理论折算的计算
以A-A截面为例,计算公式如下

(2)
①查GB50017-2003《钢结构设计规范》中表3.4.1-1钢材的强度设计值(N/mm)中,Q345钢、厚度35~50mm的抗拉、抗压和抗弯强度为f
=265N/mm。②根据GB50017-2003《钢结构设计规范》中表4.1.1中,对工字形截面,γ
=1.05,γ
=1.20;对箱形截面,γ
=γ
=1.05。③根据GB50017-2003《钢结构设计规范》5.2.2中,有端弯矩和横向载荷同时作用时,使构件产生同向曲率时,β
=1.0;产生反向曲率时,β
=0.85。④经计算,长细比λ
=λ
=27。⑤毛截面面积A
=4×(190+2×97.2)=1 537.6cm=153 760mm。⑥查《机械设计手册》第1章表2.1-87热轧H型钢尺寸规格,取W
=4×(2 220+2×1 198)=18 464cm=18 464 000mm。

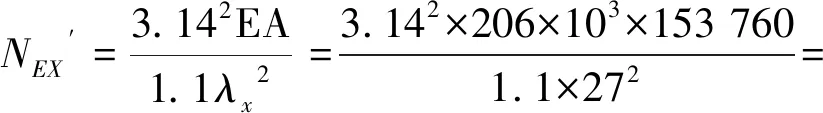
3.895×10N
⑨最大弯矩M
=5 850×10×495=2.896×10N·mm将以上①~⑨代入计算公式

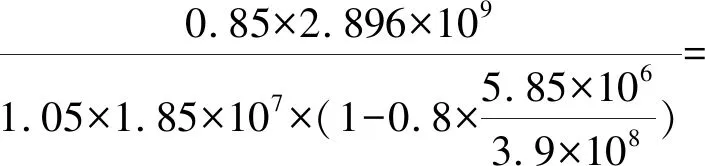
38+128.6=166.6N/mm<265N/mm
σ
<f
,在A-A截面内,塔架和底座平台的结构稳定强度(抗拉、抗压和抗弯强度)满足要求。取f
=265N/mm反推线性屈曲的临界载荷P
′=20 972 864N=20 972kN。2)B-B截面稳定性理论折算的计算
同上,计算B-B截面的稳定强度σ
=111.2N/mm<265N/mm。σ
<f
,在B-B截面内,塔架和底座平台的结构稳定强度(抗拉、抗压和抗弯强度)满足要求。3)C-C截面稳定性理论折算的计算
计算C-C截面的稳定强度σ
=22.4N/mm<265N/mm。σ
<f
,在C-C截面内,塔架和底座平台的结构稳定强度(抗拉、抗压和抗弯强度)满足要求。以上计算结果表明,钢结构塔架及底座平台的整体结构稳定性较好,不会发生整体失稳。
3 稳定性有限元仿真分析
3.1 特征值(线性)屈曲分析
单元刚度矩阵[K
]和单元几何刚度矩阵[K
]可以集成整个结构刚度矩阵[K
]和几何刚度矩阵[K
],并形成平衡方程为([K
]+λ
[K
]){δ
}={P
}(6)
式中:λ
为待定的比例因子。所以若{δ
}={0},满足以上方程式,表示没有受到外界的影响,或虽然受到外界的影响但又可以恢复到原来的平衡状态。若假设结构处于某种临界状态,即{δ
}中所有的数不全为零,但是仍然能够满足平衡条件,此时这个方程式的系数行列式必须等于零,即|[K
]+λ
[K
]|=0(7)
这就是稳定方程,求解方程得到特征值λ
,则可得到{P
}={P
}×λ
(8)
因此可得到临界载荷P
。在ANSYS分析软件中建立钢结构塔架及底座平台的有限元模型,设置预应力并执行1次静力分析,计算屈曲模态和扩展模态。对底座平台的支腿与船舶甲板安装连接处施加刚性固定的边界条件。在天车中心处建立1个独立点(MPC),将塔架顶端的节点自由度与其关联,建立刚性域。在MPC点施加预应力为-1 N,设置扩展模态值为1,比例系数为1。前6阶特征值屈曲分析的计算结果如图4所示。前4阶特征值屈曲模态如图5所示。

图4 前6阶特征值屈曲分析计算结果


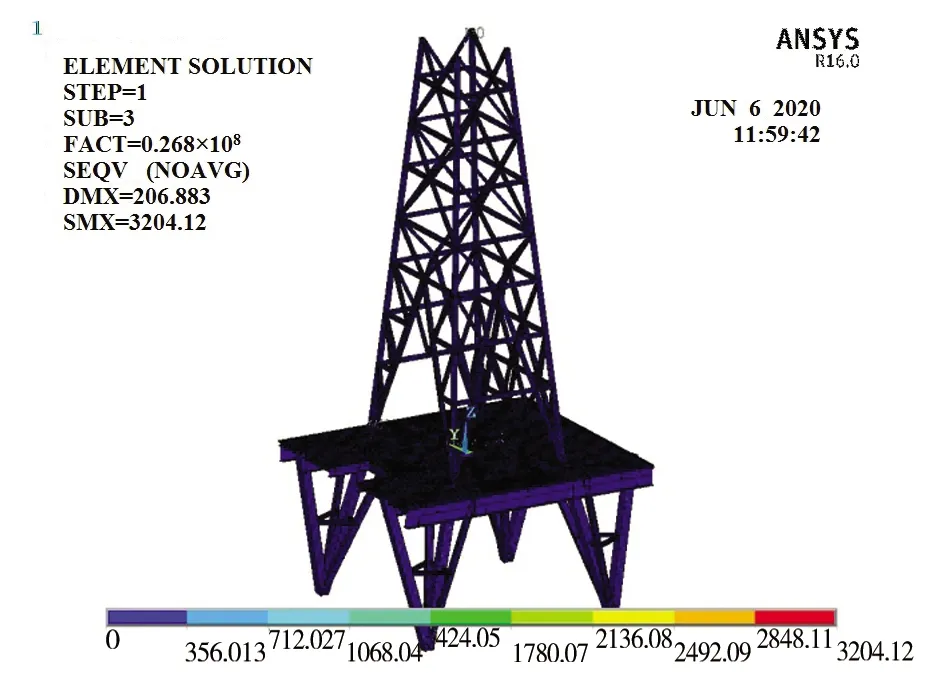
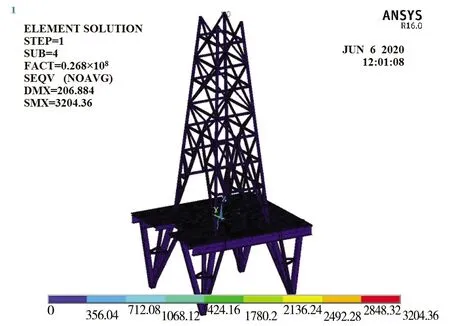
图5 特征值屈曲模态(1~4阶)
通过有限元计算方法,可以得到钢结构塔架及底座平台的失稳临界载荷(一阶屈曲载荷)为P
=0.223×10N=22 341kN,也就是说,当塔架及底座平台的载荷与失稳临界载荷相等时,塔架及底座平台结构就会出现失稳的现象。这时塔架及底座平台的变形将迅速变大,结构会丧失平衡状态,位移开始增大,直至第三阶时发生整体失稳甚至坍塌。而塔架及底座平台的最大静钩载为5 850kN,为临界失稳载荷P
的1/4,未达到临界失稳载荷,因此,钢结构塔架及底座平台不会出现整体失稳的问题。可以看出有限元分析计算出的结果与稳定性理论折算法计算的结果是相同的。通过有限元分析计算得到的临界失稳载荷P
=22 341kN,与理论折算法计算得出线性屈曲临界载荷P
′=20 972kN,结果几乎相同,两个计算结果相差仅约6.5%。说明通过理论折算法和特征值屈曲有限元分析法对钢结构塔架及底座平台的屈曲分析结果是可以相互印证的,计算结果是基本正确的。3.2 非线性屈曲分析
非线性屈曲分析是用一种逐渐增加载荷的非线性静力分析得出使结构开始变得不稳定时的极限载荷,在加载过程中慢慢增加一个不变的载荷增量值,同时该增量值使得到的结果发散,最终得到预期的临界载荷。
由结构增量形式的平衡方程可知,加载时如果将极限载荷分级加载,第i
级载荷的增量为d
{F
},可以得到下式

(9)

当所加的载荷增量增加到接近整体结构发生不稳定的情况时,此时产生的是极限载荷,迭代将会不收敛,通常情况下,就会认为此时已经达到结构极限承载能力。
在进行有限元分析时应注意以下几点:①在模型上加载初始的扰动或初始的缺陷,将一阶屈曲模态变形作为初始缺陷,使计算更准确;②打开大变形效应分析,激活应力刚化;③打开弧长法,对载荷子步进行迭代求解。
非线性屈曲分析结果如图6~图7所示。
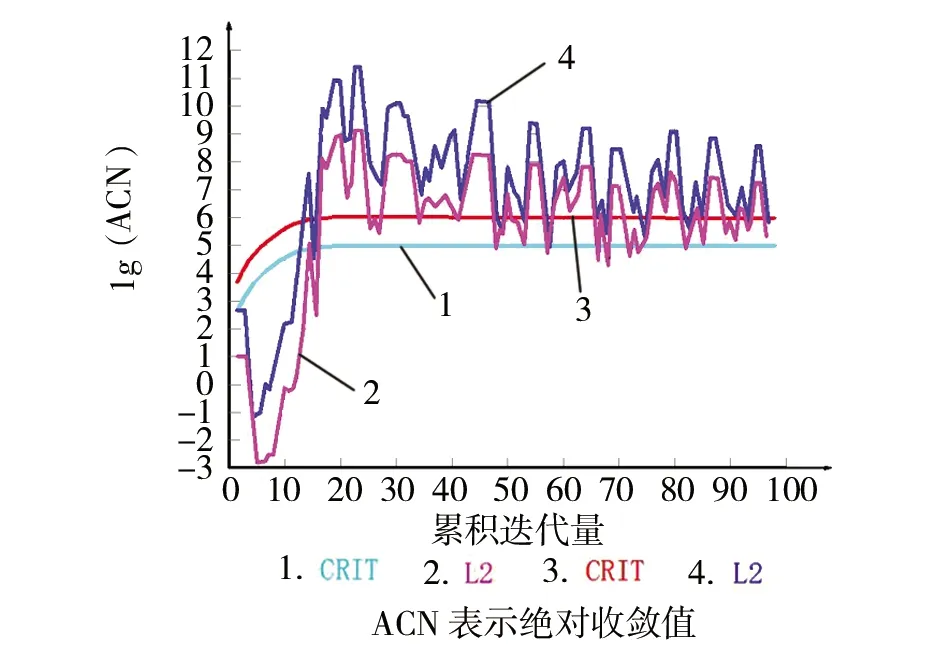
图6 非线性迭代求解收敛

图7 载荷-时间折线图
由以上结果可以看出,钢结构塔架的非线性屈曲极限载荷P
″=21 100kN,即为图7中拐点所对应的纵坐标的数值,超过这个极限载荷后,塔架及底座平台结构也失去了继续加载的能力,结构慢慢会不平衡,在时间到达某一个值时,塔架和底座平台结构的稳定性就会遭到破坏。比较特征值(线性)屈曲的临界失稳载荷P
=22 341kN与非线性屈曲的极限载荷P
″=21 100kN,结果几乎相同,两个计算结果相差仅约5.9%,其中,非线性屈曲分析的结果误差较小,相对更加准确可靠。4 结论
(1)对钢结构塔架和底座平台进行整体稳定性理论折算的计算,结果表明钢结构塔架和底座平台的整体结构稳定性较好。
(2)采用特征值(线性)屈曲和非线性屈曲两种方法对钢结构塔架和底座平台进行有限元计算分析,失稳临界载荷/屈曲极限载荷均远大于结构最大静钩载,表明钢结构塔架不会发生整体失稳。
(3)对比整体稳定性理论折算、特征值(线性)屈曲和非线性屈曲3种分析方法的计算结果,发生大变形的部位均是塔架顶部;失稳临界载荷/屈曲极限载荷数值相差较小,可相互印证,其中非线性屈曲分析的结果误差较小,相对更加准确可靠。

