隧洞爆破引起路堑高边坡振动的1/3倍频程实测分析
吕 江,赵 晖,姚 康,史 吏
(1. 杭州交通投资建设管理集团有限公司,浙江 杭州 310024;2. 浙江工业大学 土木工程学院,浙江 杭州 310023)
山岭隧道施工绝大多数采用爆破开挖,但爆破会引起隧洞本身以及周边环境的过大振动,尤其是当隧洞接近居民区、古建筑、高边坡和高等级景区时,须严格控制隧洞爆破环境振动水平。鉴于现场爆破参数、地质地形条件的复杂性,无法采用理论公式对隧洞爆破环境振动水平进行有效预测,现有研究多采用现场实测方法对周边构筑物[1-2]、文物古建筑[3]、自由场地和民居[4-5]等开展爆破振动研究。但是,针对隧洞爆破施工引起临近边坡的振动响应研究相对较少,且研究多集中于矿山或水电站边坡等范围。例如,余海兵等[6]运用数值模拟和理论分析的方法,获得了矿山边坡的振动安全阈值;刘美山等[7]和谢全敏等[8]研究了水电站边坡振动控制方法,给出了相应减振措施和安全阈值,但基本未见针对路堑高边坡隧洞开挖爆破振动的研究报道。
在爆破振动实测信号分析方面,已有的研究多集中在基于时程曲线的峰值振速和视主频方面[9-12]。事实上,爆破振动信号还包括了丰富的频率信息,卢文波等[13]建立了球形药包爆破振动的主频预测公式和衰减公式,并和工程实测数据进行了对比分析[14]。当爆破振动主频与结构固有频率相近时,易引起临近周边结构的共振破坏[15],而不同结构的固有频率是不同的[16],所以研究爆破振动在各频段的能量集中情况具有十分重要的意义。Yang等[17]和刘义佳等[18]研究也表明仅使用质点振速和视主频来评价爆破环境振动影响是不充分的,指出了考虑振动持续时间和能量集中程度的必要性。但是,现有时域最值分析无法获得振动信号的频带能量集中情况,而1/3倍频程分析能分频带呈现振速均方根值,且均方根值能表征振动能量大小[19],相较于常规的振速时域最值分析,1/3倍频程分析手段更能揭示振动信号的内涵。因此,针对上述研究的不足,笔者对隧洞爆破施工引起的路堑高边坡振动响应进行实测,通过1/3倍频程滤波获得分频段振速均方根值,继而利用萨道夫斯基公式对边坡的振速均方根值进行分频带拟合,获得路堑高边坡爆破振动的分频段场地系数K和衰减系数α。
1 工程背景
1.1 工程概况
某在建高速公路左线为路堑路基、右线为隧洞,如图1所示。该工点隧洞长度154 m,最大埋深55 m,采用钻爆法由大里程往小里程方向单向开挖。路堑分为8 级放坡开挖,坡体总高度约为60 m。现场测试期间,隧洞还剩80 m即贯穿,路堑高边坡已放坡完成,左线路堑边坡现场如图2所示。
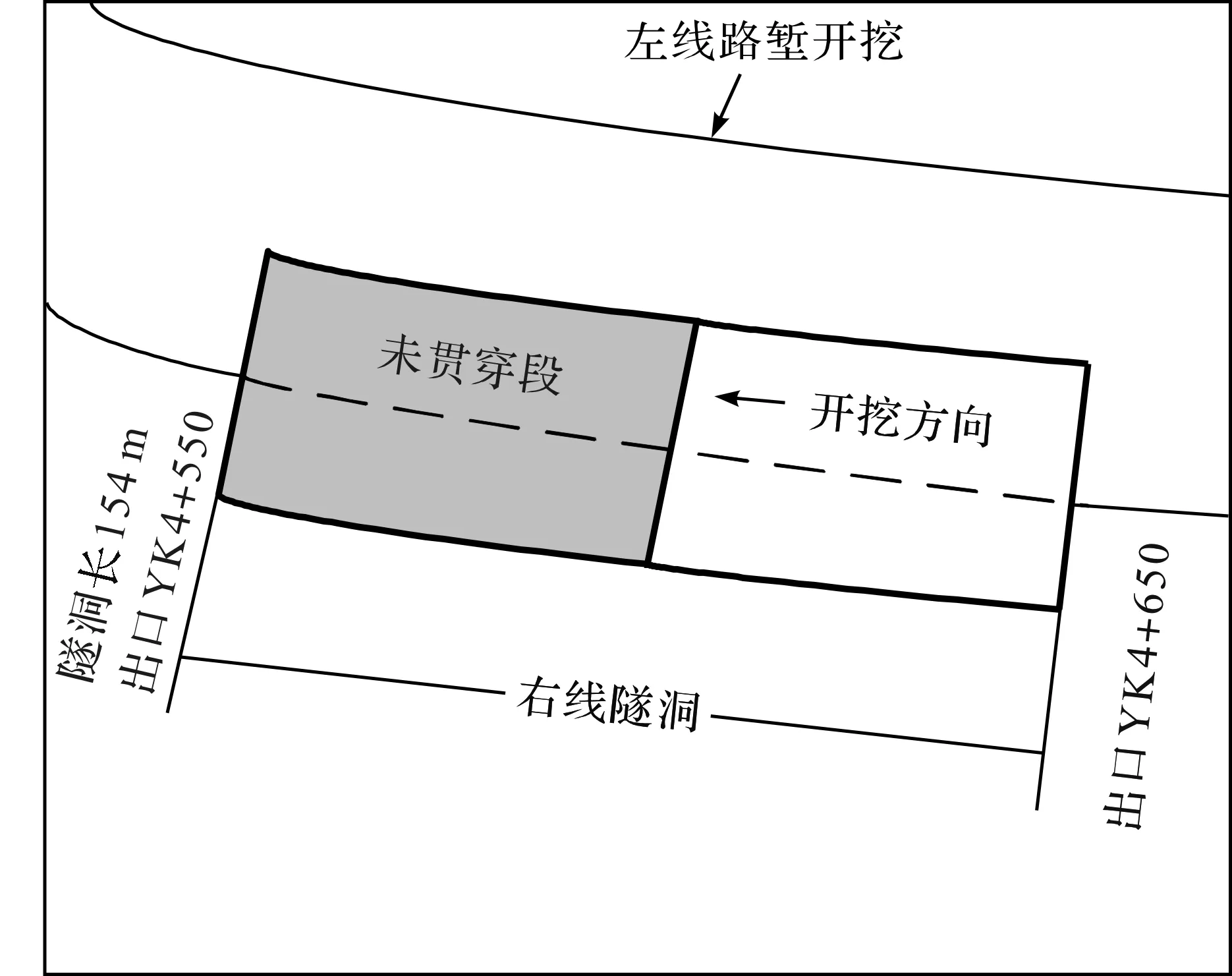
图1 隧洞和路堑平面位置图Fig.1 Schematic view on plane positions between the tunnel and the road cut

图2 隧道左线临湖地理位置现场图Fig.2 Site picture of road cut (left line of the highway)
1.2 地质条件
根据地勘资料,该工点隧洞穿越中风化泥岩和泥质灰岩层,洞身段为Ⅳ类围岩,进出洞口段为V类围岩。路堑高边坡处于强风化钙质泥岩层,岩体十分破碎。该工点的工程地质纵断面和横断面图分别如图3,4所示。

图3 隧道工程地质纵断面图Fig.3 Longitudinal geological profile of the tunnel

图4 隧道工程地质横断面图Fig.4 Cross geological profile of the tunnel
1.3 爆破方案
隧洞采用台阶法进行爆破施工,炮眼直径42 mm,不耦合装填药卷直径32 mm的2#岩石乳化炸药,药卷规格为0.3 kg/节。上台阶和下台阶炮孔的装药量分别为0.9,0.6 kg/m,炮孔装药长度为1~5 m,采用毫秒微差起爆。由于隧洞掌子面已接近洞口的V类围岩,岩体较为破碎,所以各爆破回次的总装药量控制在25~50 kg,控制各回次爆破进尺为0.5~1.5 m。以第8次爆破为例,上、下台阶的炮孔布置情况如图5所示,相关爆破参数汇总如表1所示。
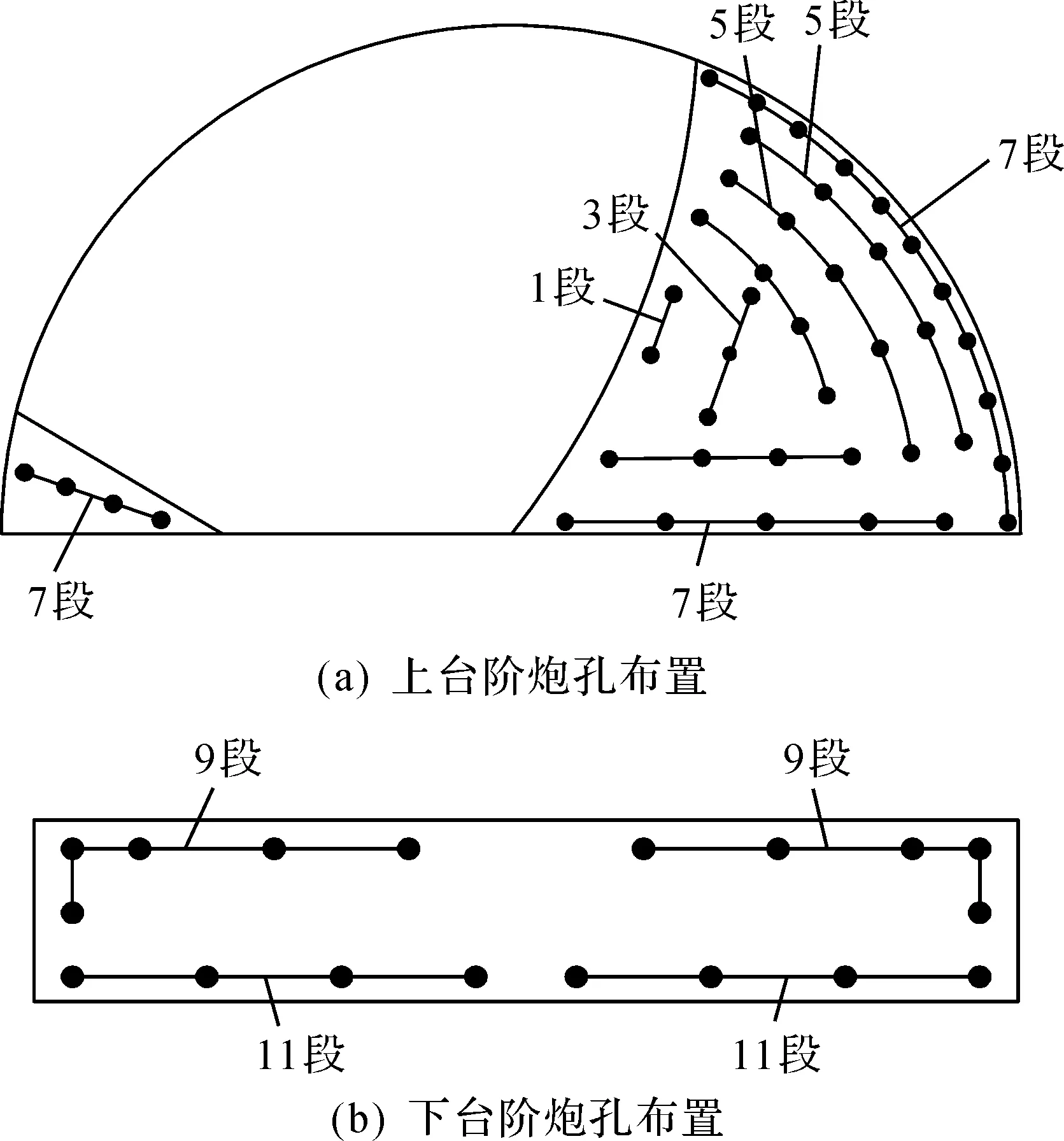
图5 第8次爆破炮孔布置图Fig.5 Blasthole layout for the 8th blasting
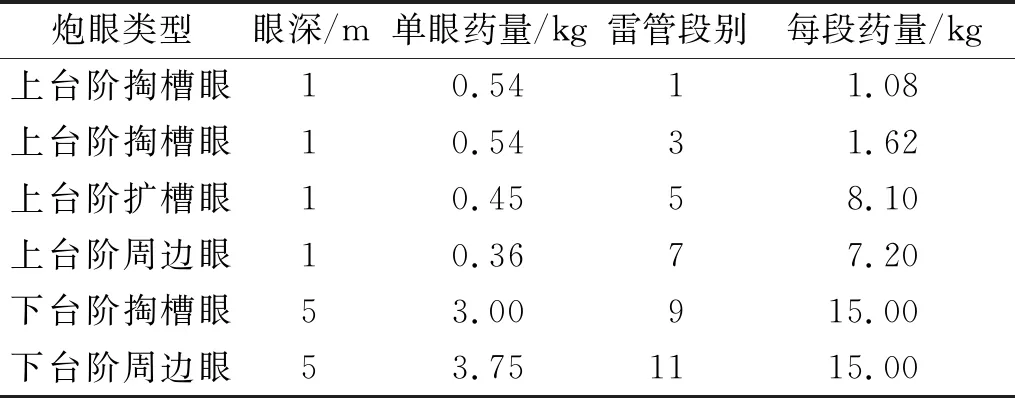
表1 爆破开挖参数Table.1 Blasting excavation parameters
2 现场测试
2.1 测点布置和测试仪器
在左线路堑边坡的第2,3,4级放坡平台上分别布置三向振速传感器各1 只,在右线隧洞已开挖段的洞内侧壁上布置三向振速传感器1 只,各测点位置相对位置如图6,7所示。各测点振速传感器安装方向:x向为爆源方向,z向为铅垂方向,水平y向与x向垂直。传感器灵敏度26 V/(m·s-1),通频带为1~500 Hz,数据采集使用TC-4850测振仪,采样频率8 000 Hz,触发振速0.01 cm/s。现场测试期间,各测点爆心距随爆破回次的变化情况汇总如表2所示。
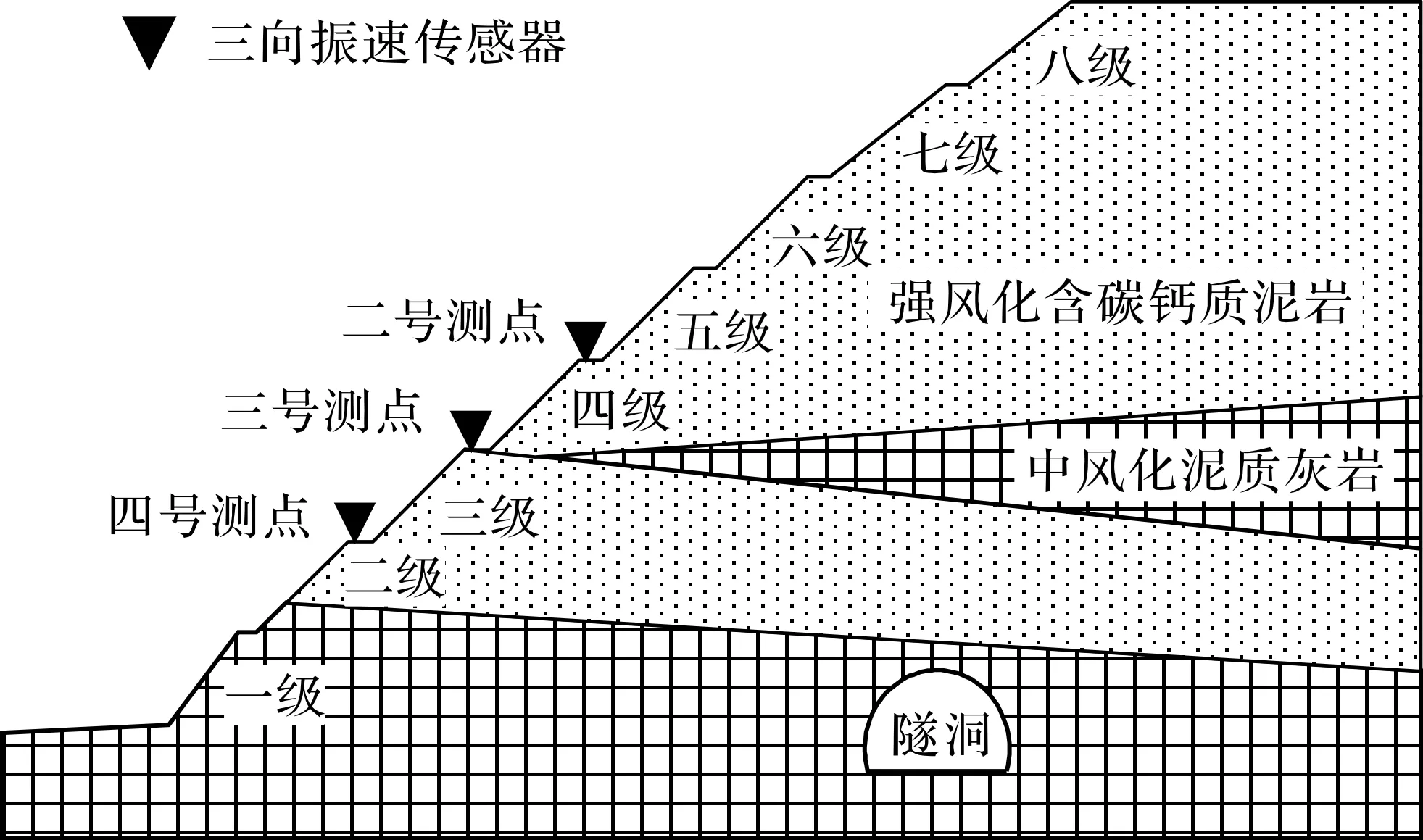
图6 左线路堑边坡振速测点布置图Fig.6 Schematic view on velocity sensors on the cutting slope

图7 隧道洞内振速测点布置图Fig.7 Schematic view on velocity sensor inside the tunnel
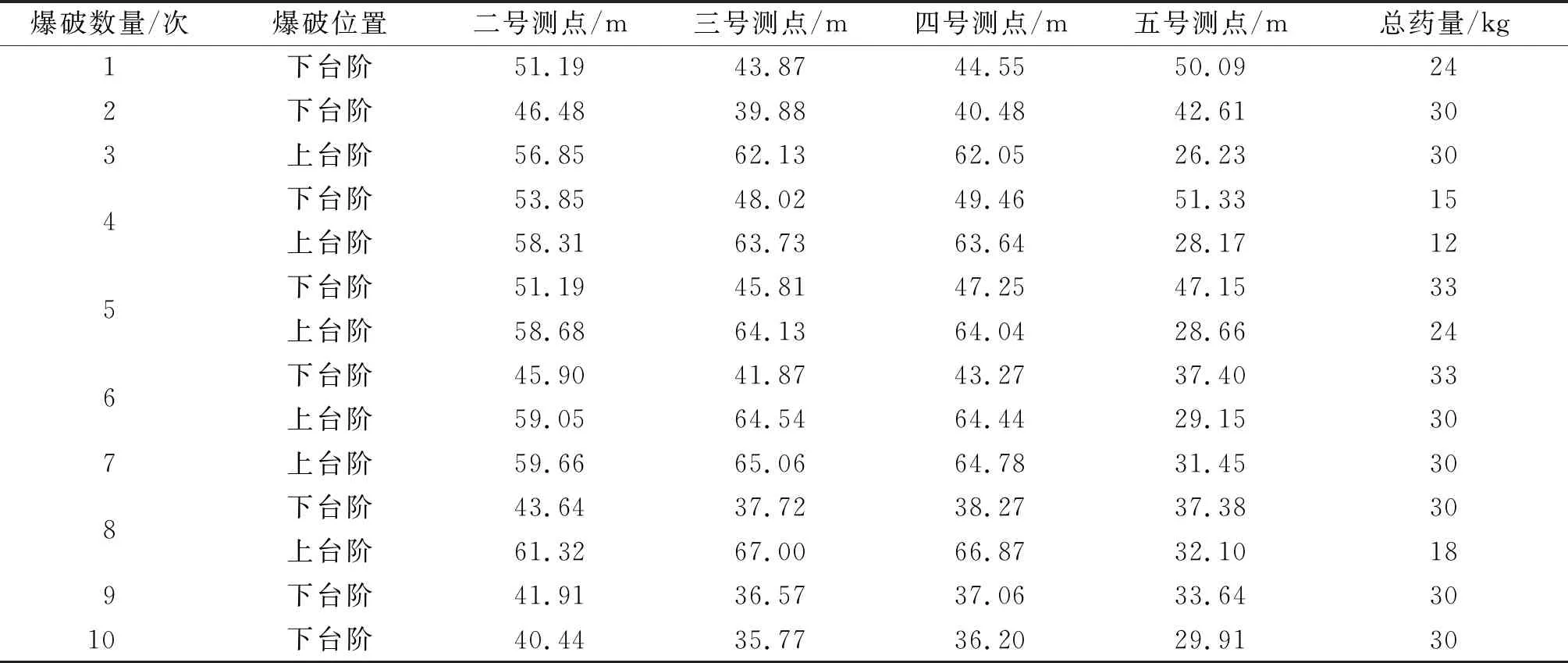
表2 各测点爆心距变化Table 2 Blasting distance at different sensor locations
2.2 典型爆破振动信号
各段别炮孔以毫秒微差的形式先后起爆,如图5所示,由现场爆破施工方案以及文献[20]可知各段别的延时时长如表3所示。第8次爆破时边坡三号测点和洞内五号测点的实测振速时程曲线如图8所示。由洞内五号测点,清楚可见各段别起爆所贡献的振速峰值(图8b),峰值时差与表3基本对应。但由于振动从掌子面经由岩体传至边坡测点时会发生干涉、弥散和衰减等现象,使得边坡测点实测振速峰值时差(图8a)与表3的对应性不再明显。

表3 各段别毫秒延时雷管的延时时长Table 3 Delay time of detonators
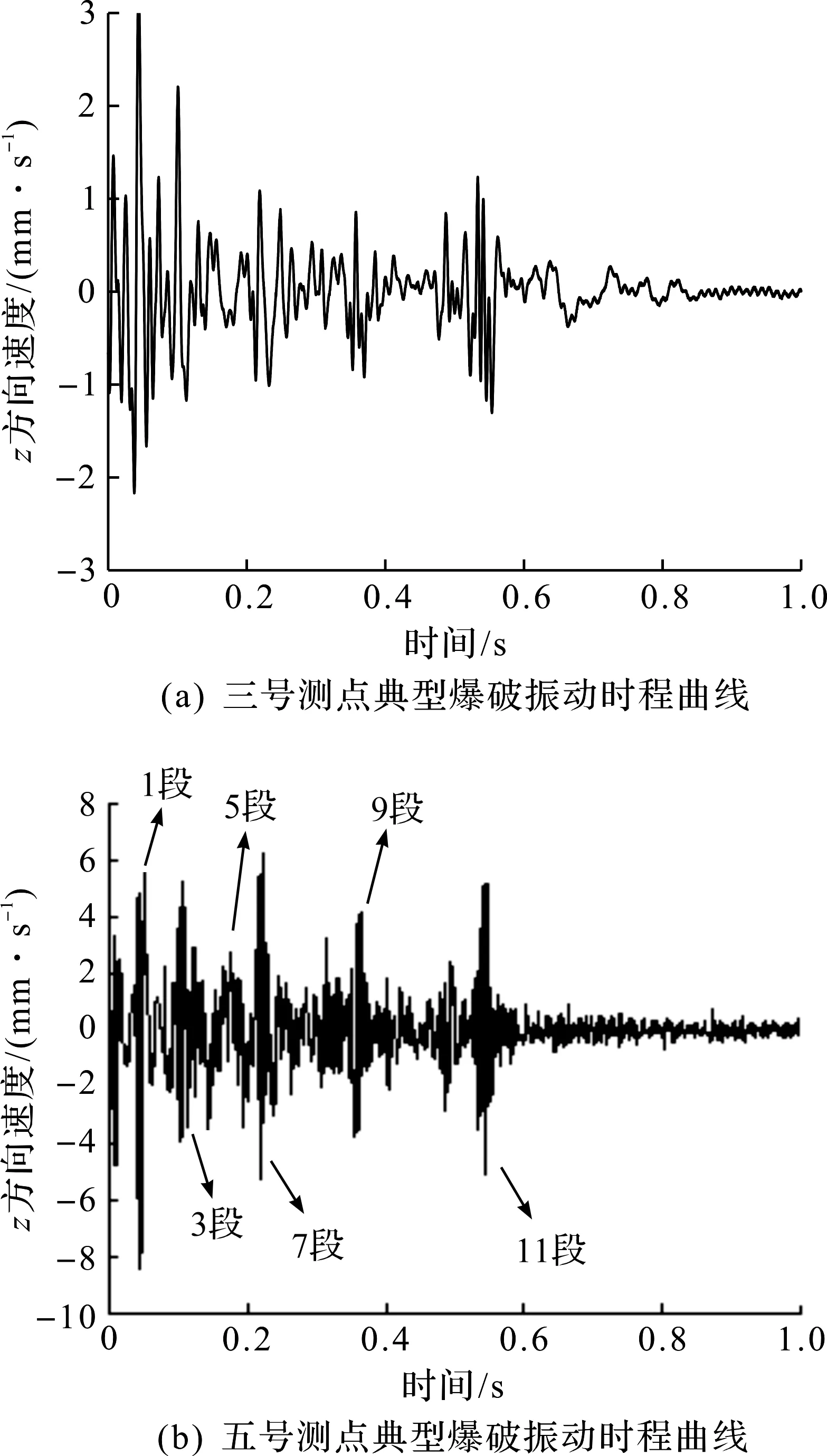
图8 典型振速时程曲线Fig.8 Typical vibrational velocity time histories
3 实测振速的1/3倍频程分析
3.1 1/3倍频程
由实测振速信号的频谱分析可知:边坡测点的振动响应频率集中在200 Hz以内。根据文献[21]可将0~200 Hz划分为24 个频段,各频段的中心频率分别为1,1.25,1.6,2,2.5,3.15,4,5,6.3,8,10,12.5,16,20,25,31.5,40,50,63,80,100,125,160,200 Hz,各频段的上下限分别由中心频率乘以和除以21/6获得。
1/3倍频程分析的本质是在时域信号Fourier变换的基础上,对上述各频段进行滤波,分离出位于该频段的振动频域信号后再进行Fourier逆变换,获得相应的振速时域信号并取均方根值,从而作为当前频段所对应的振速代表值。振速均方根值能体现振动信号的有效能量大小,因而相较于常规的时域最值分析,1/3倍频程分析更能准确描述振动信号的频率和能量特性。
3.2 边坡和洞内测点的1/3倍频程对比
对于边坡测点而言,振动能量是以体波(几何阻尼1/r)穿越全风化岩层(岩体破碎、材料阻尼大)入射至各边坡测点。对于洞内测点而言,爆破能量从掌子面出发,主要以柱面SH波形式沿着已开挖隧洞洞壁传播至五号测点(基本无几何阻尼),加之隧洞主要处于中风化层、岩体相对完整(材料阻尼小)且爆心距较短,可认为振动能量传至洞内测点时的衰减很小,即洞内五号测点基本代表了掌子面的爆破振源特性。因而,可以通过边坡和洞内测点的振速对比来体现爆破振动由振源传至边坡过程中的衰减特性。
以第8次爆破为例,洞内和边坡测点振速信号的1/3倍频程曲线对比情况如图9所示。由图9可知:对于边坡测点(二~四号点)而言,振动能量主要集中在12~75 Hz;对于洞内测点(五号点)而言,除上述频带外,振动能量还在175 Hz附近出现峰值。对于75 Hz 以上的各频段,洞内测点远大于各边坡测点,说明了爆破振动传播过程中发生了明显的高频衰减。
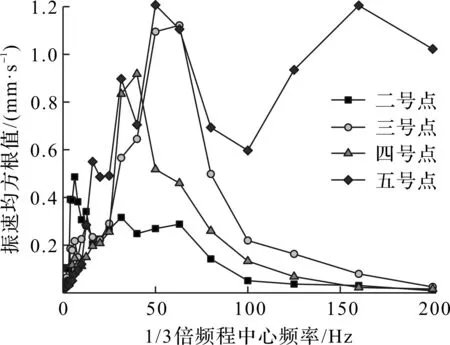
图9 第8 次爆破1/3倍频程图Fig.9 1/3 octave band for the 8th blasting
为定量评价爆破振动传至边坡过程中的衰减情况,定义衰减系数为
(1)
式中:Si为边坡i号测点相对于洞内测点的衰减系数;Vi为边坡i号测点的各频段振速均方根值;V5为洞内五号测点的各频段振速均方根值。
边坡各测点衰减系数在各爆破回次下的统计值如表4~6所示。以表6所示的四号测点为例,在40 Hz以内的低频段,相对于隧洞振源出现了明显的振动放大现象(即各频段的S4为负数);对于50~200 Hz的高频段,则出现了明显的振动衰减现象(S4为正数),200 Hz时的衰减系数均值达0.9,表明爆破振动波的高频分量在入射至边坡时基本衰减完全。如上所述,爆破振动经由掌子面穿越全风化岩层时,各频段的振动能量均会衰减,但低频段相对于高频段衰减更慢。因而,低频分量的振动波入射到边坡自由面时,其振速相对于振源衰减较少,边坡自由面的反射波与上述入射波干涉叠加,因此边坡测点相对于振源出现低频段的放大现象。而对于高频分量的振动波,其到达边坡自由面之前已发生明显的衰减,即使边坡自由面的反射波与明显衰减的入射波干涉叠加,最终高频段的坡面振动也会明显低于振源。将二号(表4)和三号(表5)测点的各频段衰减系数与表6对比可知:两者的低频放大效应更明显。考虑到二号和三号测点高程比位于四号测点大,说明存在边坡振动的高程放大现象。二、三、四号点相邻高差分别为10,9.3 m,二号和三号测点相对于坡脚四号测点的低频振动放大情况如图10所示。与唐海等[22]的实测数据有较好的吻合度,说明了图10所得衰减比例的可靠性。由图10可知:0~15 Hz频段,二号和三号测点的高程放大效果与高差有较好的一致性,即高差越大、放大效果越明显,高程放大比例约为0.88 cm/(s·m),说明该频率范围的爆破振动主要激发了边坡的“鞭梢效应”振动模态。而对于在15 Hz以上的频段,放大效果与高差的一致性不再明显,说明边坡高阶振动模态基本无“鞭梢效应”。
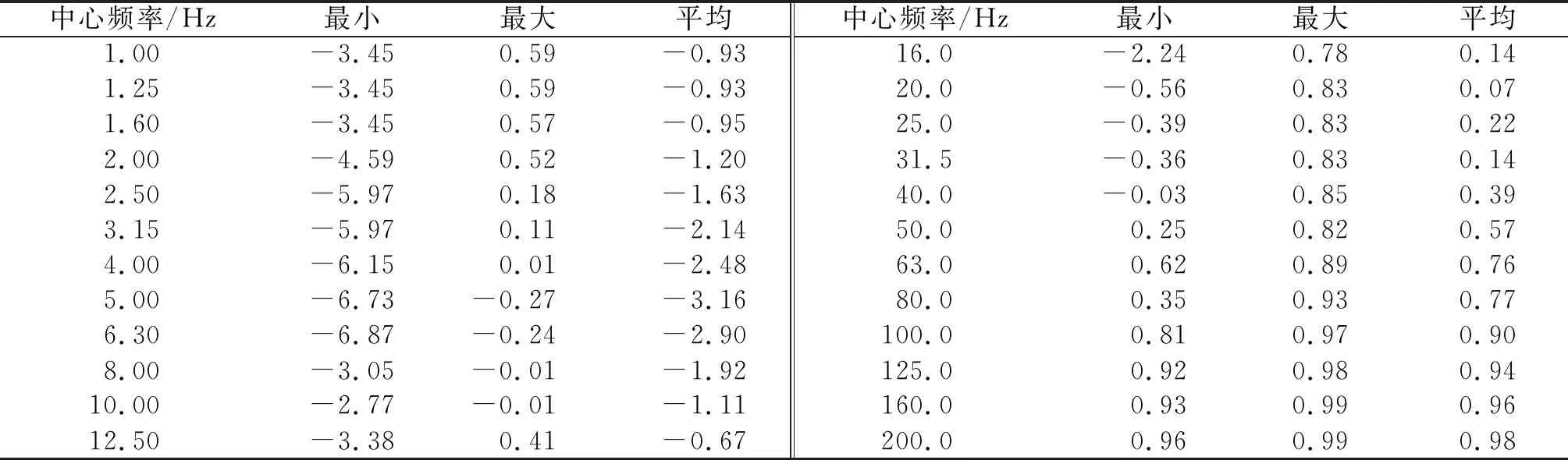
表4 边坡二号测点各频段衰减系数统计值Table 4 Statistical values of attenuation coefficients of each frequency band forsensor No.2 on the cutting slope
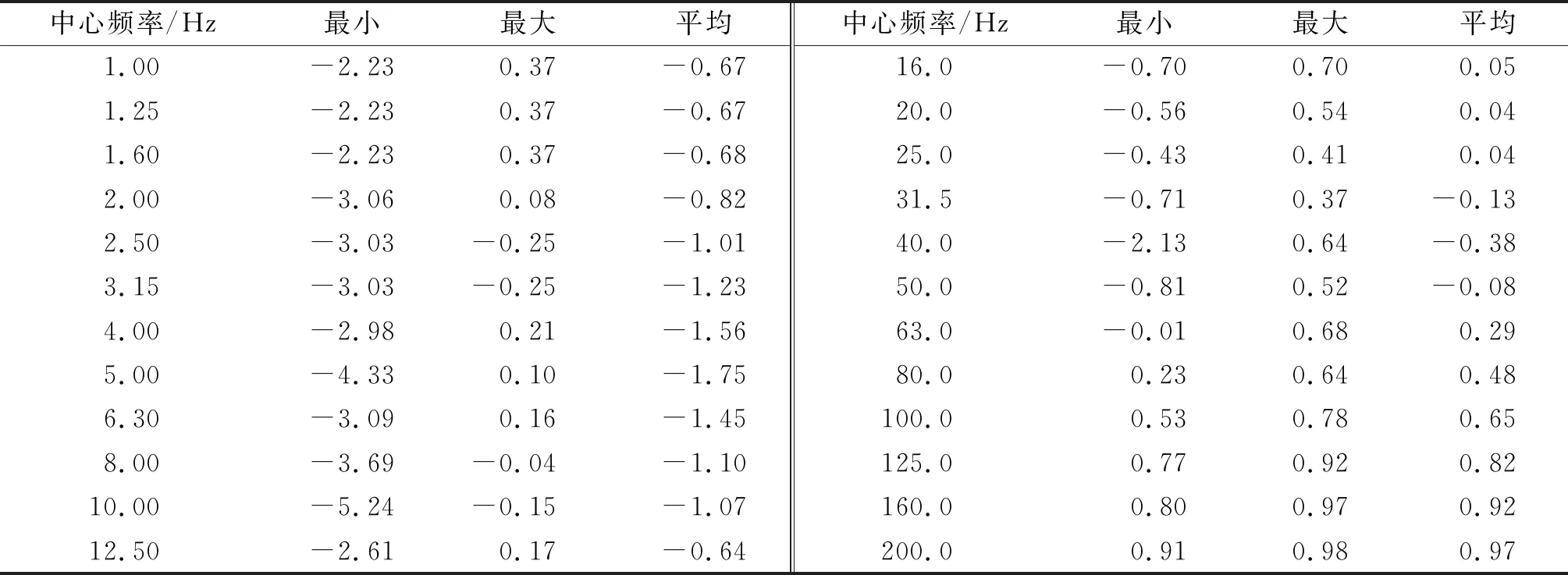
表5 边坡三号测点各频段衰减系数统计值Table 5 Statistical value of attenuation coefficient of each frequency band for sensor No.3 on the cutting slope

表6 边坡四号测点各频段衰减系数统计值Table 6 Statistical value of attenuation coefficient of each frequency band for sensor No.4 on the cutting slope
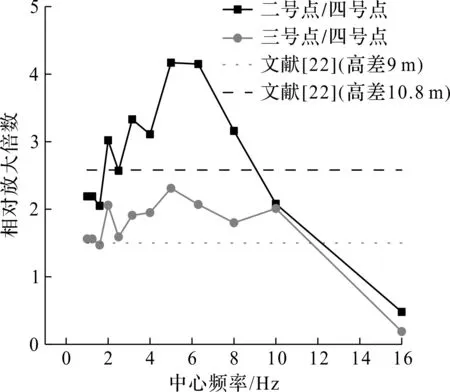
图10 边坡测点低频衰减系数图Fig.10 Attenuation coefficientsat low-frequency bands for sensors on the cutting slope
3.3 振速均方根值的分频段拟合
如前所述,不同环境对象对振动频率的敏感程度不同。同时,对于爆破振动这种持续时间短、峰值大的冲击振动而言,其响应均方根值更能体现振动的能量水平。因此,有必要分频段拟合振速均方根值随装药量和爆心距的变化情况,从而建立高边坡振动的分频段振速均方根值拟合公式。
此处,利用萨道夫斯基公式拟合边坡测点各频段的振速均方根值随单段药量和爆心距的变化情况,分频带萨道夫斯基公式为
(2)
式中:Q为单段药量,kg;R为爆心距,m;Vn为频带n的振速均方根值;Kn和αn分别为频带n的待定场地系数和衰减系数。式(2)两边取对数,以方便进行最小二乘法线性拟合,线性关系式为
(3)
具体拟合时,首先将某次爆破时振速总时程上各段别炮孔贡献的振速时程分隔提取;其次进行1/3倍频程分析获得各频段的振速均方根值;最后取本次爆破爆心距为R(表2),取本段炮孔药量(表1)作为Q,取1/3倍频程频段n的振速均方根值Vn,确定ln(Q1/3/R)~ln(Vn)坐标系中的一个数据点。表2所示10 个爆破回次的所有炮孔段别均使用上述流程拟合,可在双对数坐标系中获得一系列离散数据点,再依据式(3)进行最小二乘法线性拟合,从而获得当前频段振速均方根值的拟合公式。以第8次爆破的洞内测点(五号测点)为例,在双对数坐标系中,该测点80 Hz频段(n=20)所对应的散点图如图11所示,线性拟合可得该频段的拟合表达式为
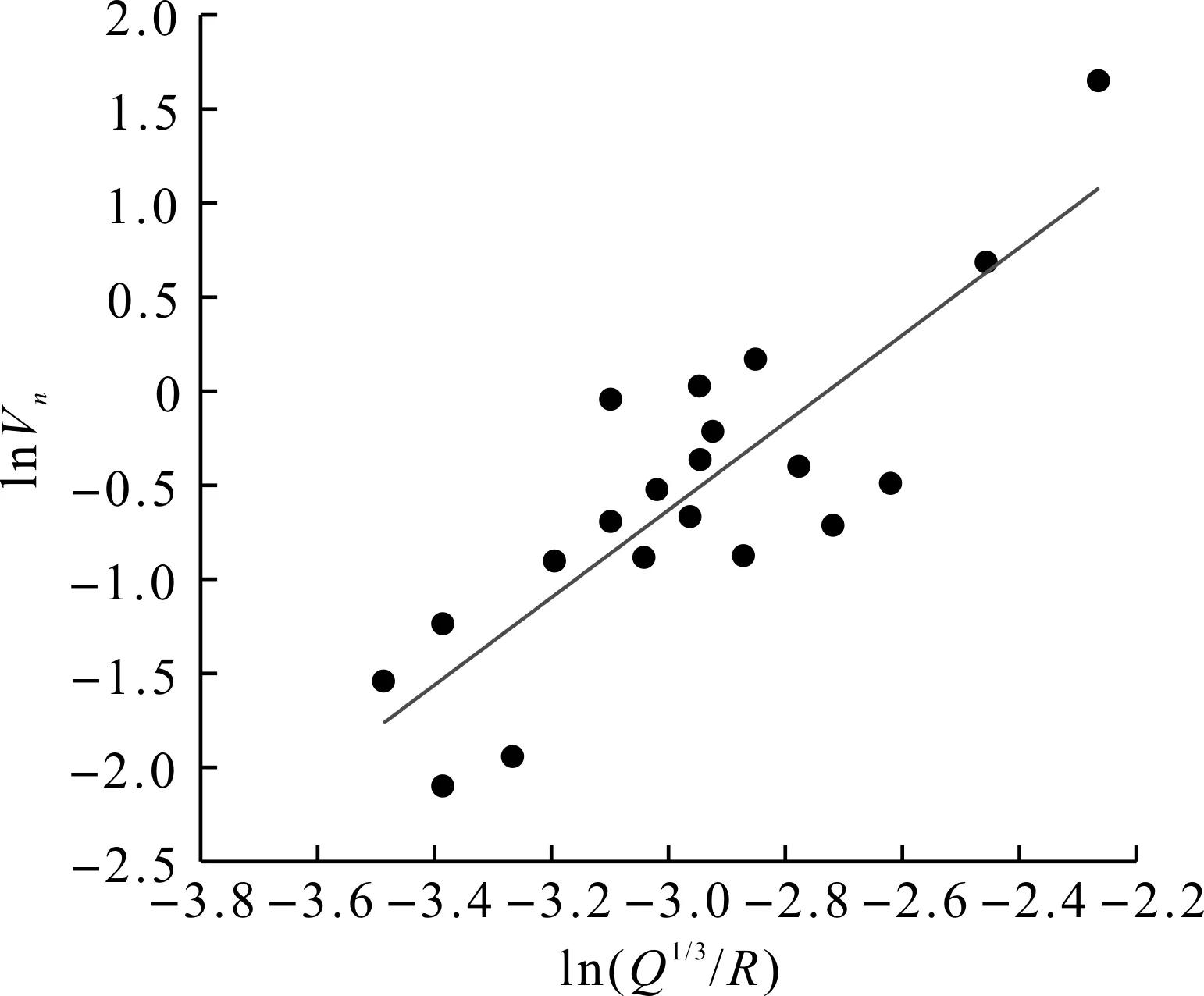
图11 五号测点80 Hz频带(n=20)振速回归直线Fig.11 The regression line of the vibration velocity of the 80 Hz(n=20) frequency band for sensor No.5
(4)
式中:场地系数K20=57.9;衰减系数α20=1.49。相关系数为0.70说明拟合度较好。
重复上述分析流程,可得边坡和洞内各测点的分频段振速均方根值拟合公式,各测点的场地系数和衰减系数对比情况分别如图12,13所示,具体系数取值汇总如表7所示。

图12 各测点的分频带场地系数KnFig.12 Field coefficients Kn at different frequency bands and sensor locations
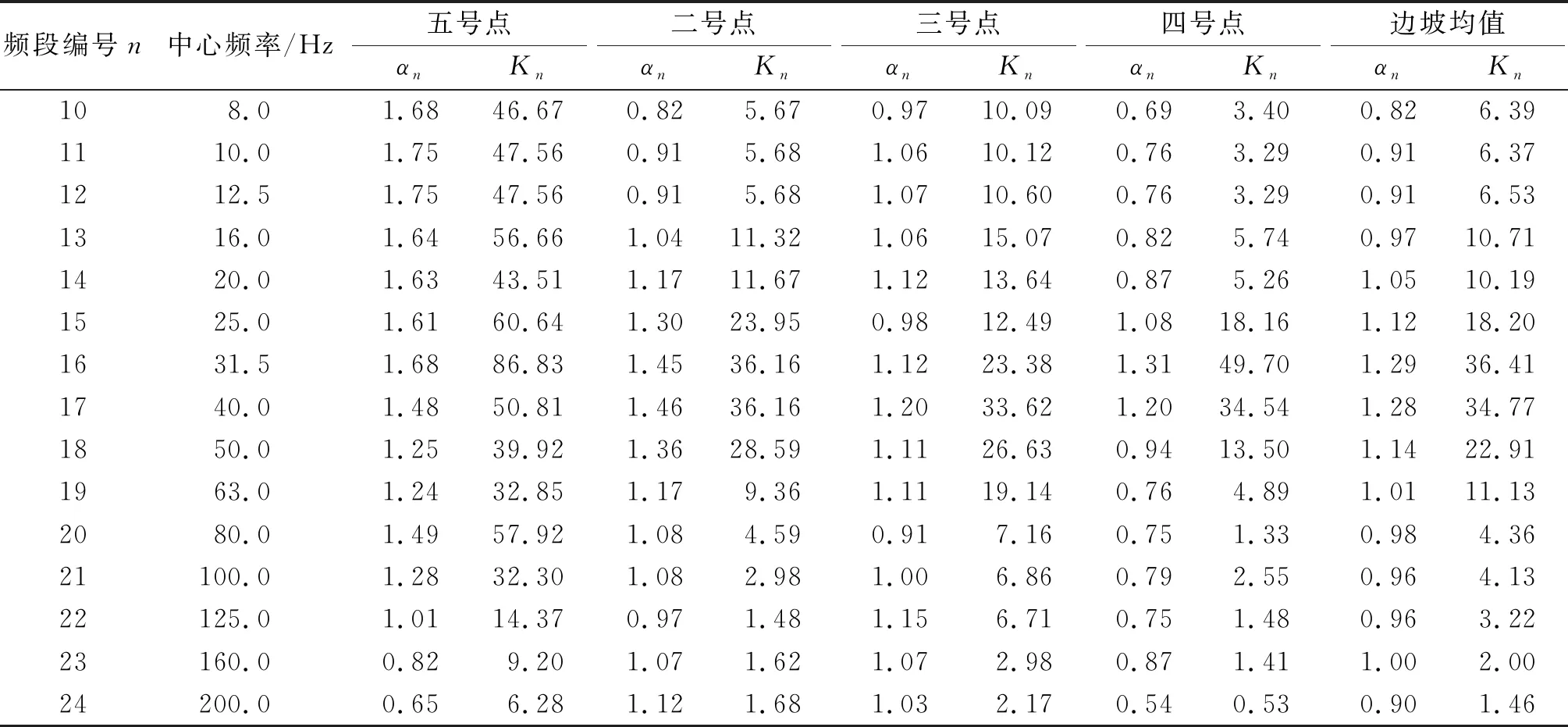
表7 各点位分频带拟合结果Table 7 Fitting results of each frequency band
由图12,13可知:洞内和边坡振动的场地系数和衰减系数均呈现明显的频率依赖性,且洞内测点的场地系数明显高于边坡测点。对于边坡3 个测点而言,各频段的场地系数Kn十分接近,但衰减系数αn离散性较大,说明边坡振动的高程放大效应主要由αn体现。因此,对图12中3 个边坡测点的Kn进行平均作为坡体的场地系数,但αn还需根据边坡观察点的具体位置来确定,但为了方便边坡振速的初步估算,表7和图13仍给出了3 个边坡测点的αn平均值作为坡体的衰减系数。根据Kn和αn均值(表7),可直接运用式(2)进行隧洞爆破施工引起路堑高边坡振动的分频段预测。为了进一步探究两个系数在80 Hz处出现突变的原因,将此爆破回次的装药量和爆心距代入卢文波等[23]的主频预测公式中,计算得到主频范围在80~105 Hz,而80 Hz正好在此范围内,说明了Kn和αn会在爆源峰值频率出现突变。
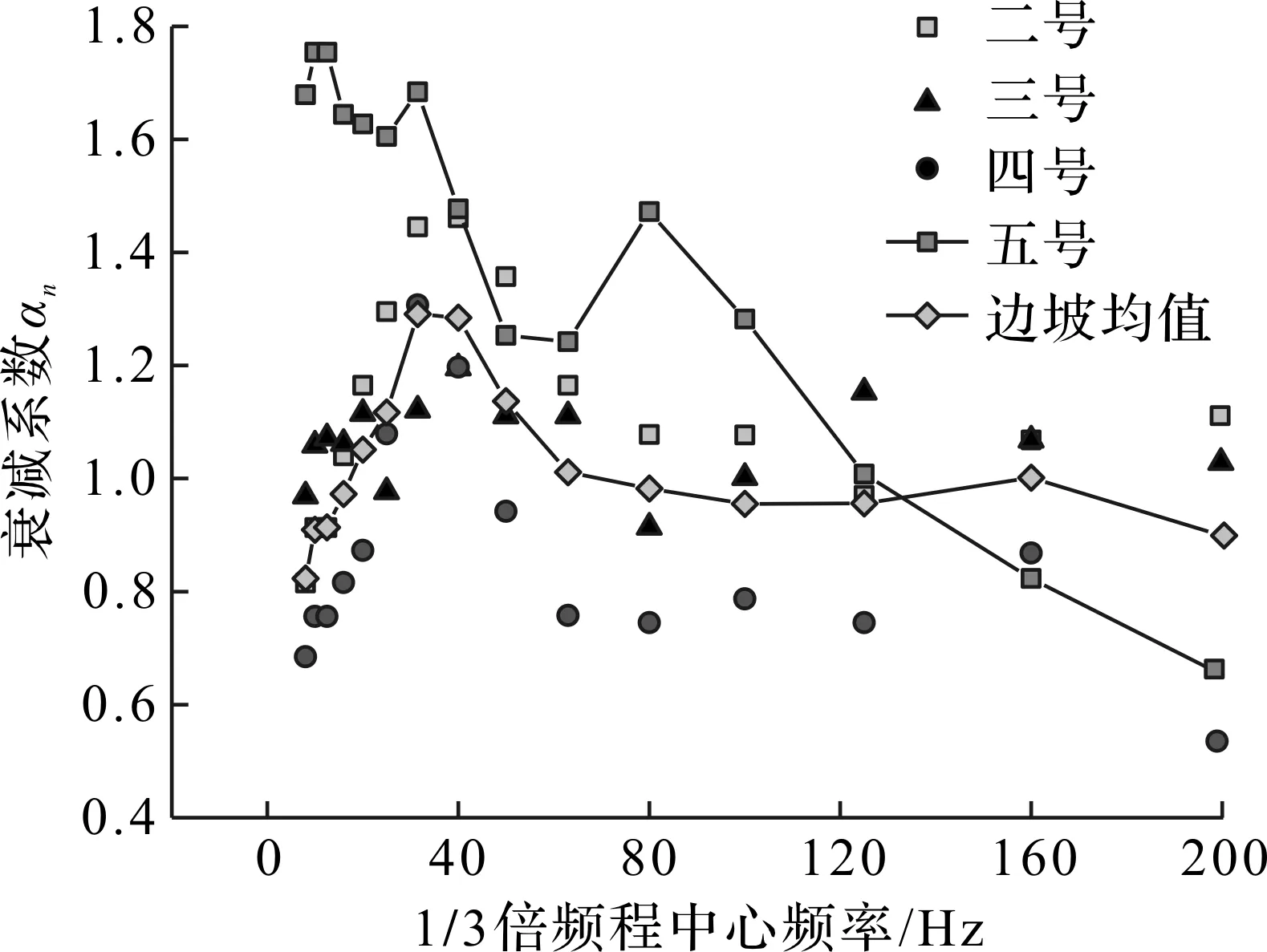
图13 各测点的分频带衰减系数αnFig.13 Field coefficients αn at different frequency bands and sensor locations
4 结 论
笔者实测了隧洞爆破开挖引起的洞内以及邻近路堑高边坡的振动响应水平,对实测振速数据进行1/3倍频程滤波,获得了洞内和边坡测点的分频段振速均方根植,分析了爆破振动经由隧洞传至边坡过程中能量集中频带的变化情况。在此基础上,分频段拟合获得了萨道夫斯基公式的场地系数K和衰减系数α,可用于预测洞内和边坡的各频带振速均方根值随装药量和爆心距的变化情况。主要结论:1) 对于边坡测点而言,振动能量主要集中在12~75 Hz范围,对于洞内测点而言,振动能量在50 Hz和175 Hz附近出现峰值,75 Hz以上频段的振动能量从洞内传播至边坡过程中衰减明显;2) 隧洞爆破环境振动的低频部分(0~15 Hz)可引发路堑边坡的“鞭梢效应”振动模态,使得低频段的边坡振动出现了明显的高程放大现象;3) 提出了隧洞爆破引起路堑高边坡振速均方根值的分频段萨道夫斯基预测公式,可用于预测隧洞爆破施工引起临近高边坡振动能量的频率分布情况。

