桩-筒组合基础水平受荷性能数值模拟研究

何 奔，姜贞强，王晓强，潘晓东，袁宗浩，史 吏

(1.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311100；2.浙江工业大学 土木工程学院， 浙江 杭州 310023)

海洋风机的基础形式众多，水深30 m以内的近海海域多采用重力浅基础、吸力筒基础或单桩基础[1]。为进一步增强基础的水平承载性能，近年来工程界提出了一种新型基础形式——大直径单桩-筒体组合基础。p—y曲线是公认的描述风机桩基础非线性水平变形(y)和水平承载力(p)的有效分析方法，p—y曲线法最早由Matlock[2]依据黏土中小直径短桩的水平受荷模型试验提出。近年来，不少专家学者利用单元体试验[3]、数值模拟[4-5]和模型试验[6-7]等多种手段，对不同土体和结构参数影响下的风机基础p—y曲线进行了研究。在大直径单桩方面，孙冬梅[4]和何奔[5]通过数值模拟发现现有p—y曲线并不能直接适用于大直径单桩，并结合模型试验提出了适用于软黏土中大直径单桩的修正p—y曲线；朱斌等[6]和黄茂松等[8]对大直径单桩在静力和循环荷载下的p—y曲线进行研究，并对美国石油协会(API)规范推荐p—y曲线进行修正[9]。在桩-筒组合基础研究方面，刘润等[10]分析了单桩和筒体各部分对桩-筒组合基础竖向和水平承载能力的贡献；吕阳等[11]利用ALE(任意拉格朗日-欧拉法)技术研究了黏土中吸力筒沉贯过程中的大变形问题，分析了沉贯阻力和土塞高度等问题；通过模型试验；Andersen等[12]发现增大吸力筒基础埋深，能提高吸力筒的水平抗倾覆能力；黄周泉等[13]分析了竖向荷载作用下桩-筒组合基础桩外侧摩阻力、土压力及桩身轴力的分布规律，得到了筒体加固对桩-筒组合基础竖向承载力的提升程度；刘文白等[14]对竖向荷载下的桩-筒组合基础几何尺寸进行了优化组合。

由以上综述可知：相较于大直径单桩和吸力筒基础，目前针对桩-筒组合基础的研究较少，且多限于竖向承载特性。笔者在ABAQUS中建立桩-筒组合基础的三维有限元分析模型，研究筒体对大直径单桩水平和抗倾覆承载能力的提升程度,并根据模拟结果对API规范推荐的p—y曲线进行修正，使其适用于桩-筒组合基础的水平受荷计算。

1 有限元模型

以位于杭州湾平湖海域的某海上风电场工程为研究背景，该风电场涉海面积约48 km2，规划容量300 MW。风场中心点离岸约20 km，水深为8～12 m。场区内海底地形变化较小，海底滩面最大坡度小于1°，适合采用单桩基础或者吸力筒基础。将单桩基础与吸力筒基础结合，得到桩-筒组合基础，如图1所示。在实际施工中，为了避免施工中支腿船和稳桩平台无法施工，先进行桩基础施工。第一步，将桩基础下沉到指定深度后停止下压；第二步，将筒基础套入桩基础中，采用负压使筒基础下沉至泥面与筒盖位于同一水平面；第3步，抽出筒基础护筒与桩基础之间间隙中的泥浆，并进行水泥灌浆填充，连接桩基础与筒基础，完成施工[15]。

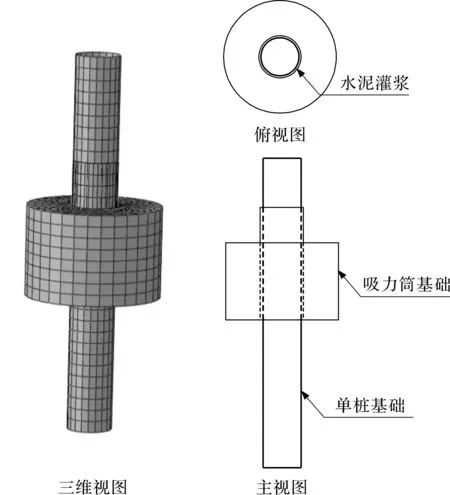
图1 结构示意图Fig.1 Structural diagram

1.1 模型处理及参数选取

模型中钢管桩桩径d=6 m，桩长l=50 m(其中入土深度为30 m)，管桩厚径比δ/d=1%(壁厚δ=6 cm)；由于筒体为单桩基础的加固结构，为节省材料，壁厚δ=2 cm，直径D、高度h见表1；地基长度和宽度为25d，桩底以下土层深度为8.3d，静力分析中可以忽略边界效应的影响[16]。

表1 模型筒参数Table 1 Parameters of the bucket 单位：m

风机基础桩体和筒体均为钢材(Q345C)，考虑为理想弹塑性材料，其屈服强度=325 MPa，杨氏模量E=2.1×108kPa，泊松比υ=0.25。土体采用摩尔-库伦(M-C)本构模型。利用风电场勘察取样土体，以有效总应力法进行室内单元体试验，获得了土的物理力学参数，具体参数见表2。

表2 土的物理学参数Table 1 Parameters of the soil

1.2 网格划分、接触及约束

土体的单元类型采用八节点六面体减缩积分单元(C3D8R)，并增强沙漏刚度，此单元对位移求解精度更高并且不会产生剪切自锁。桩体和筒体的单元均采用四结点曲面通用壳(S4)，采用有限膜应变，壳单元更加适合分析大直径钢管桩的特性。

由于实际工程中桩体和筒体内护筒之间采用的是水泥灌浆连接，因此模型中采用“Tie”的方式连接桩与筒，将其接触面设置为刚性连接，模拟实际工作中的桩-筒基础在位情况；桩体/筒体与土体的接触面设为面-面接触对，遵循摩尔库伦摩擦定律，法向行为选为“Hard”Contact，摩擦特性选为“Penalty”，摩擦系数由土体内摩擦角决定，按tan(0.75φ)[17]取值。土体侧面限制水平向位移，底面完全固定，顶面自由无约束。

1.3 有限元模拟过程

在实际状况中，土体内部有地应力存在，在进行桩的水平加载前必须进行初始地应力平衡。具体分析步骤如下：第一步，创建自动地应力平衡分析步，对完整的土体施加重力使之平衡，以创建初始地应力场；第二步，创建静力分析步，激活桩体和筒体，同时进行桩土接触的设置；第三步，对桩顶部进行水平位移(荷载)加载，以考虑桩在海浪冲击及上部结构传递下来的水平荷载。

2 模型试验验证

针对近海风机电场超大直径单桩，Zhu等[18]基于常重力条件下刚性桩无量纲比尺对应关系，取杭州某基坑粉土，开展了模型比尺为1∶30的桩基模型试验。笔者选取上述模型试验中密实度为88%的一组粉土作为数值模拟对象。

利用ABAQUS 1∶1建立数值模型，进行有限元数值建模，整个地基模型为长方体，长方体地基的长和宽为桩基直径的20倍，桩底距模型底部为5倍桩径，本构模型选取为M-C，模型桩的参数与粉土的计算参数见表3。

表3 验证模型的参数Table 3 Parameters of verification model

图2给出了当加载点高度分别为1D，3D，6D时，数值模拟所得加载点荷载位移曲线与试验结果的对比。当加载高度为1D时，数值模拟结果与模型试验结果拟合较好。由图2可知：在加载的前段曲线两者几乎一致；当加载高度为3D时，模拟结果与实验结果有着一定差距，但荷载位移曲线的变化规律仍然较为一致；当加载高度为6D时，同样可观察到两种方法计算结果几乎重合。图3为桩身无量纲转动中心深度的数值模拟结果和试验结果的对比[18]。当荷载较小时，模型试验得到的无量纲转动中心位置呈现出较大的离散性，但随着荷载的逐渐增大，转动中心的位置逐渐趋于稳定，其变化范围为0.75L～0.85L。图3所示的数值模拟结果显示：在整个加载过程中无量纲转动中心位置并没有出现太大的离散性，其变化范围为0.70L～0.75L。数值模拟结果与试验结果[18]相比，无量纲转动中心位置的聚集性更好，且总体变化规律与室内模型试验结果较为一致。以上分析表明：ABAQUS模拟的结果能正确反应实际工况下的无量纲转动中心变化规律。经过上述分析可以得出：数值模拟的结果与Zhu等[18]试验结果非常接近。因此，模拟静力使用M-C本构模型模拟土体，采用面-面接触的土体/结构接触设置模拟土体/结构之间的接触行为具有相当的可靠性。

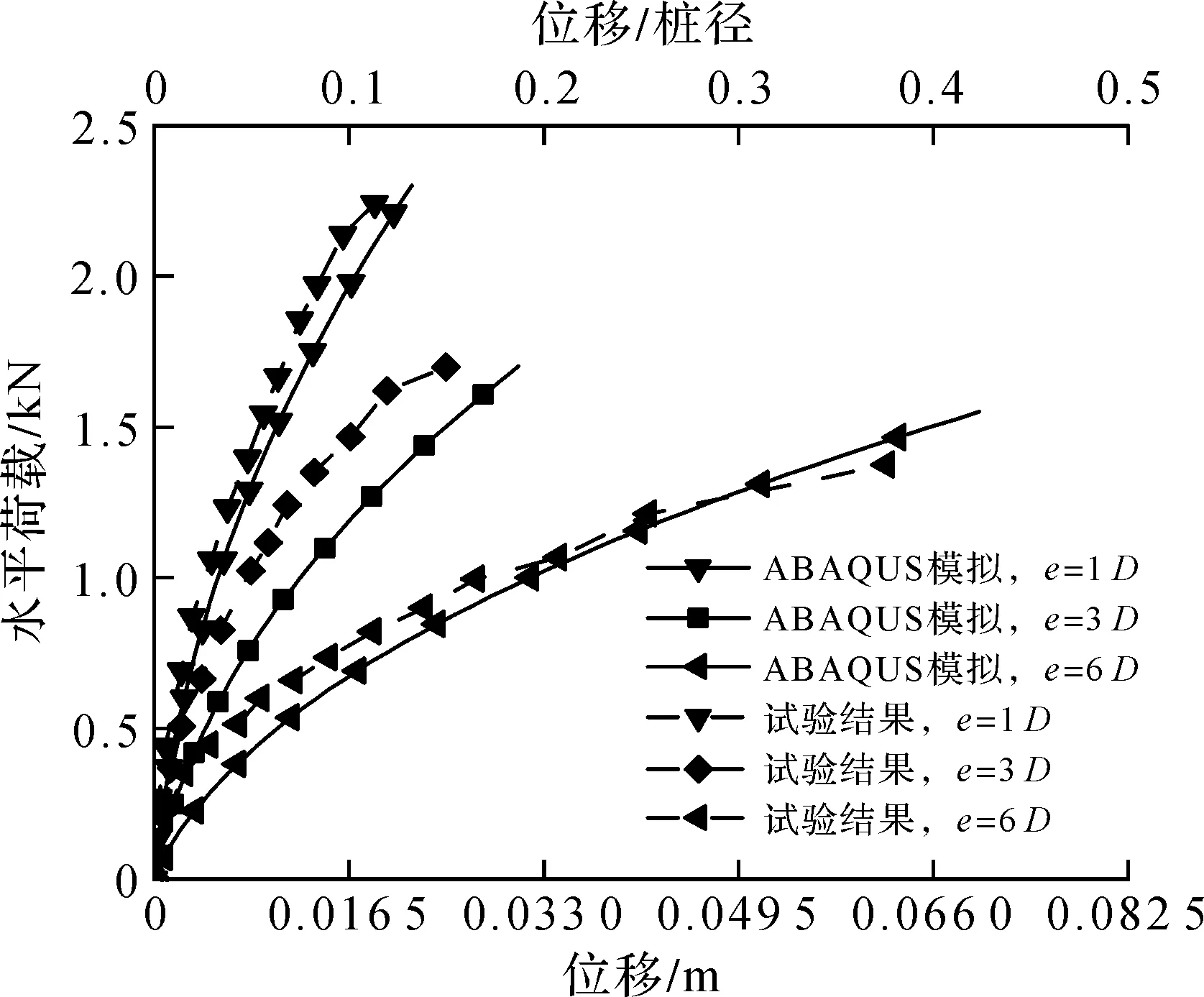
图2 荷载—位移曲线Fig.2 Load-displacement curves at loading point

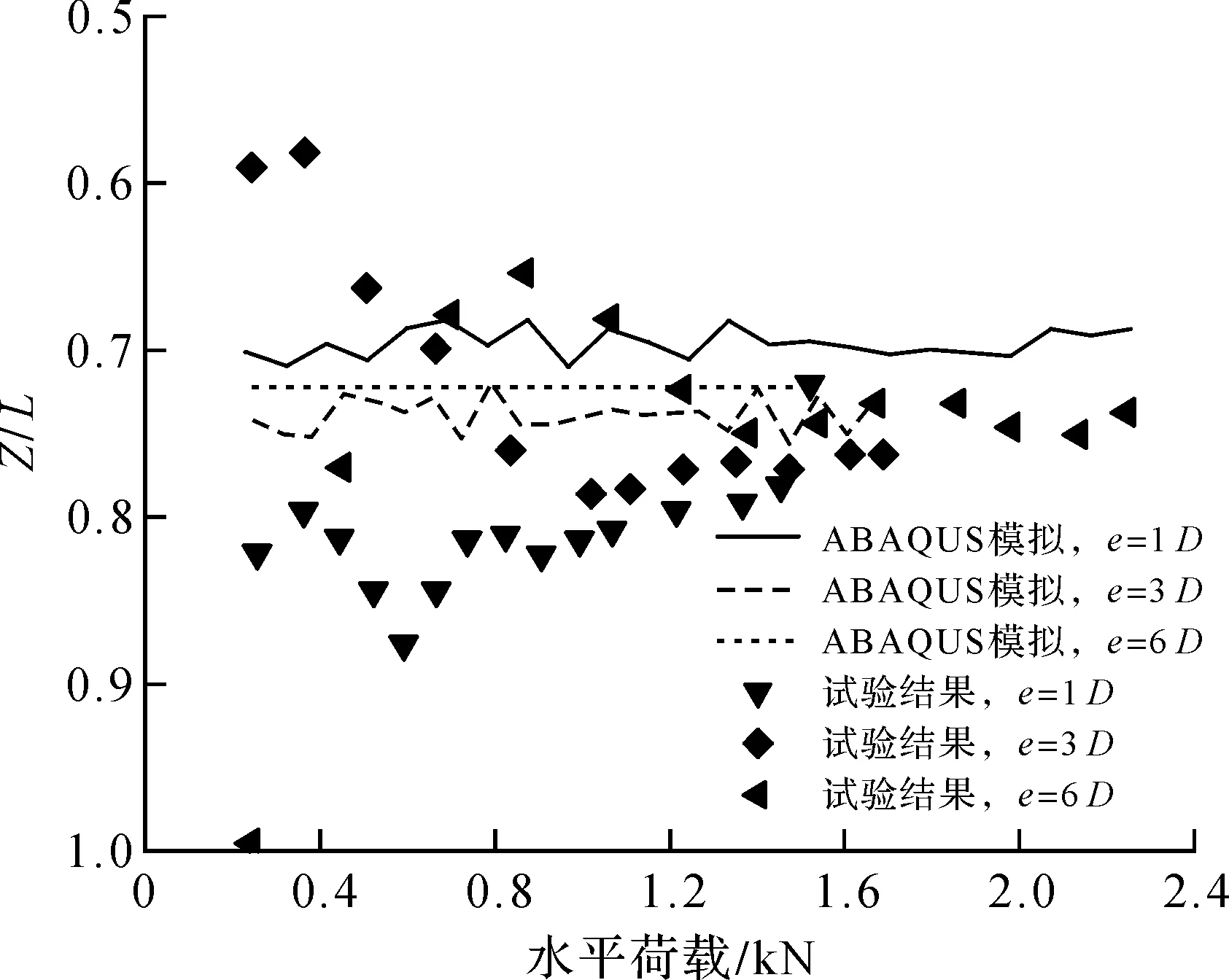
图3 无量纲转动深度Fig.3 Locations of rotational centers

3 桩-筒组合基础有限元计算结果

根据《风电场工程技术标准：风电机组地基基础设计规定(试行)》(FD 003—2007)和实际工程中对于风机基础泥面处转角的控制，在桩顶部加载0.17 m水平位移，控制桩基础在泥面处转角在0.5°以内[19]。为对比分析筒体对单桩基础的加固效果，除桩-筒数值模型外，笔者还建立了大直径单桩基础模型，并在第三步分析结束以后，读取桩身的水平位移、剪力和弯矩情况，并与桩-筒模型进行比较。

3.1 桩-筒组合基础承载力分析

单桩基础在水平荷载作用下，主要由3d～5d深度范围内的土体提供水平抗力[20]，为此在该深度范围内设置筒体最为有效。计算中筒高选取为h=1d，2d，3d，筒径选取为D=3d，4d，5d，对上述尺寸的桩-筒组合基础进行建模，并通过位移加载控制桩基础在泥面处转角为0.5°，分析不同D和h下筒体对单桩基础的加固效果。

表4给出了大直径单桩和不同尺寸的桩-筒基础的水平承载力。从表4可以得到：筒径每增加1倍桩径可以提升约49.07%的水平承载力，筒高每增加1倍桩径可以提升约28.17%的水平承载力。经过对比分析，增加筒径的加固效果相较于增加筒高的效果高19%～23%。因此，在规范允许的变形条件下，筒体对单桩基础有着很显著的加固效果，筒径D和筒高h是影响加固效果的两大因素，相较于筒高，筒径对桩-筒组合基础水平承载力影响更大。

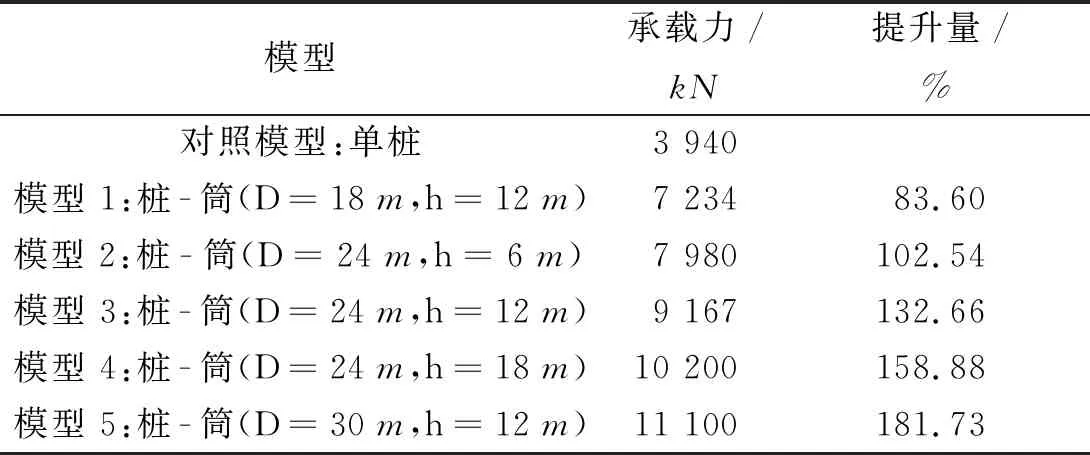
表4 承载力提升情况Table 4 The increment of bearing capacity

3.2 桩-筒组合基础位移与土反力

3.2.1 基础水平位移规律

图4为5种加载工况下单桩基础与桩-筒组合基础(D=18 m，h=12 m)水平位移沿深度的变化曲线。根据Poulos and Hull的判定标准[21]进行验算，直径d=6 m、厚径比δ/d=1%的单桩为刚性桩。如图4所示，单桩基础的变形模式为典型的刚性单桩。单桩基础在进行筒体加固后，基础上部刚度有较为显著的增加，在水平荷载作用下，基础的转动中心明显上移，整个桩-筒组合基础的位移特征与刚性单桩的位移特征相似。

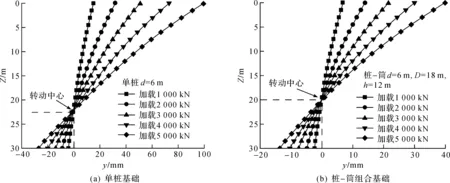
图4 基础水平位移Fig.4 Lateral displacement of the foundation

3.2.2 基础土反力分布规律

桩-筒组合基础的加固段在增加基础刚度的同时，相应也会承担更大部分的水平土反力。图5展示了5 种加载工况下单桩基础与桩-筒组合基础(D=18 m，h=12 m)土反力的分布情况。单桩基础桩周土反力沿深度方向分布较为均匀，主要由2d深度以内的桩周土提供土反力。桩-筒组合基础与单桩基础呈现明显不同的情况，在相同的荷载条件下，筒体加固段的基础承担了绝大部分的土反力，基础的其余部分承受的土反力相较于加固段明显减小。结合3.2.1中的基础水平位移规律可发现：桩-筒组合基础的土反力转折点深度与单桩基础明显不同，单桩基础的土反力转折点深度与其转动中心深度一致，桩-筒基础土反力转折点深度与筒体底端相同。

图5 基础土反力分布Fig.5 The soil reaction force distribution of the foundation

综合上述分析可知：增加筒径可以扩大基础对桩周土的影响范围，使得更多的浅层土体为基础的水平承载力提升作贡献；而增加筒高则不然，超过2d深度的桩周土对基础水平承载力提升的作用本身就不大。因此，增加筒高对基础水平承载力的提升效果远不如增加筒径。

4 桩-筒组合基础p—y曲线分析

4.1 桩-筒组合基础p—y曲线

表5给出2.25 m和3.75 m深度处大直径单桩(d=6 m)及不同尺寸组合下的桩-筒基础的水平极限土反力Pult，并将桩-筒基础的水平极限土反力与单桩基础进行对比。由表5可知：在浅层土体中，API规范低估了大直径单桩的水平极限土反力；增加筒体加固形成桩-筒基础后，水平极限土反力可提升7倍以上；在筒体加固的深度范围内，增加筒体的高度会对某一深度处的水平极限土反力提升起到负作用。本节通过ABAQUS有限元模拟计算得到的桩-筒组合基础不同深度处的p—y曲线。计算筒体加固段桩身受到的水平极限土反力，记录于表6，可以看出桩-筒组合基础加固段桩身受到的水平极限土反力随深度增加而显著提高。

表5 pult提升情况Table 5 The increment of pult

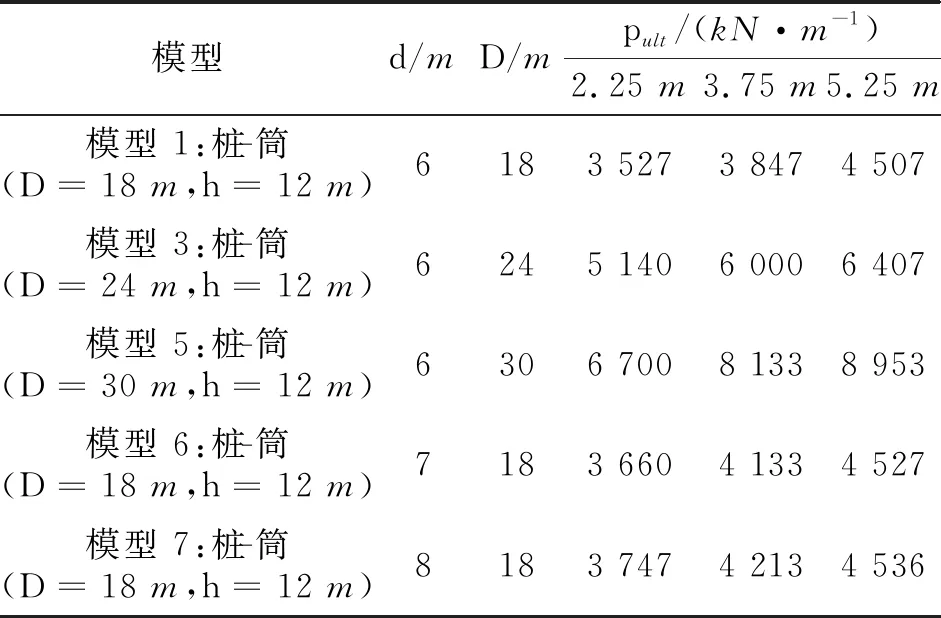
表6 桩侧土体水平极限土反力Table 6 Lateral limit soil reaction

与此同时，为判断桩径d对筒体加固深度范围内p—y曲线的影响，建立厚径比δ/d=1%，加固筒直径D=18 m，高度h=12 m的有限元模型进行分析，可得到图6所示桩-筒组合基础加固段的p—y曲线。可图6可知：在筒直径和高度不变的情况下，桩径的变化对桩-筒组合基础加固段桩身受到的水平极限土反力影响甚微，而且随深度增大影响明显减小。因此，在修正p—y曲线时，暂不考虑筒高范围内桩径影响。

图6 桩-筒组合基础p—y曲线图Fig.6 p-y curve of pile-bucket combination foundation

由以上分析可知：桩-筒组合基础的桩身位移、土反力分布以及p—y曲线的形式与单桩相似，在建立桩-筒组合基础的p—y曲线时，可以根据API规范推荐的单桩p—y曲线进行修正。

API规范推荐的静力作用下，黏土中的p—y曲线表达式为

(1)

式中：p为距离地表深度为z处，桩身受到的水平土反力，kN/m；pult为桩身沿深度方向单位长度上的水平极限土反力，kN/m；y为距离地表深度为z时，桩身的水平变位，m；y50为桩周土达到水平极限土反力一半时，对应的桩身水平变位，m；ε50为原状土样的室内三轴试验中，竖向最大应力的一半处发生应变；d为计算宽度，单桩基础中为桩的直径，m。

静力作用下的水平极限土反力值pult的计算式为

(2)

式中：Su为原状土试样的不排水抗剪强度，kPa；γ为土的重度，kN·m-3；zr为水平极限土反力转折点深度，m；J为经验系数，取0.25～0.35，一般在正常固结的黏土中取0.5。

由式(1，2)可知：pult，y50是建立桩-筒组合基础p—y曲线的关键参数。参考胡烨之等[22]提到的大直径加翼桩p—y曲线修正方法，对以上参数进行修正，即可得到桩-筒组合基础的p—y曲线。

4.2 修正水平极限土反力pult

根据式(2)可知：土体深度小于zr时，桩身受到的水平极限土反力与不排水抗剪强度Su、土体重度γ、深度z以及计算宽度d相关。不排水抗剪强度反映了土体的强度特征，其值与深度z有关。由于3.2.1节已经验证，桩-筒组合基础中的桩径对p—y曲线加固段影响微小，在桩-筒组合基础中计算宽度可以认为与筒径相同。土体参数与计算宽度已知的情况下，API规范推荐曲线中水平极限土反力可以转化为与深度z有关的一元函数。在式(2)中添加修正系数后可得

(3)

式中：ds为计算宽度；D为筒直径，m。

钱家欢等[23]通过三轴压缩试验(UU，CU，CD)结合工程实践的方式，发现限定应力范围内使用M-C破坏理论计算岩土问题与实测结果较为符合。水平极限土反力转折点以上土体应力较小，可采用与深度呈现线性关系的抗剪强度计算公式，即

su=c+γztanφ

(4)

将式(4)代入式(3)可得

(5)

根据上文土反力分布结果，水平极限土反力转折点位于筒体底端，同级荷载作用下，桩-筒组合基础筒加固段范围外土反力分布与单桩吻合较好[25]。因此，API规范中对于zr以下的pult计算公式仍可适用于桩-筒组合基础。桩-筒组合基础的zr即筒体底端所对应的深度。

依据数值模拟结果，使用最小二乘法求解式(5)中待定系数A，B，C，然后反解出e，f，g，并建立水平极限土反力转折点深度以上的公式，即

(6)

修正后p—y曲线的水平极限土反力值与该文有限元模拟结果见图7，可以发现修正后结果与有限元模拟结果拟合趋势一致。

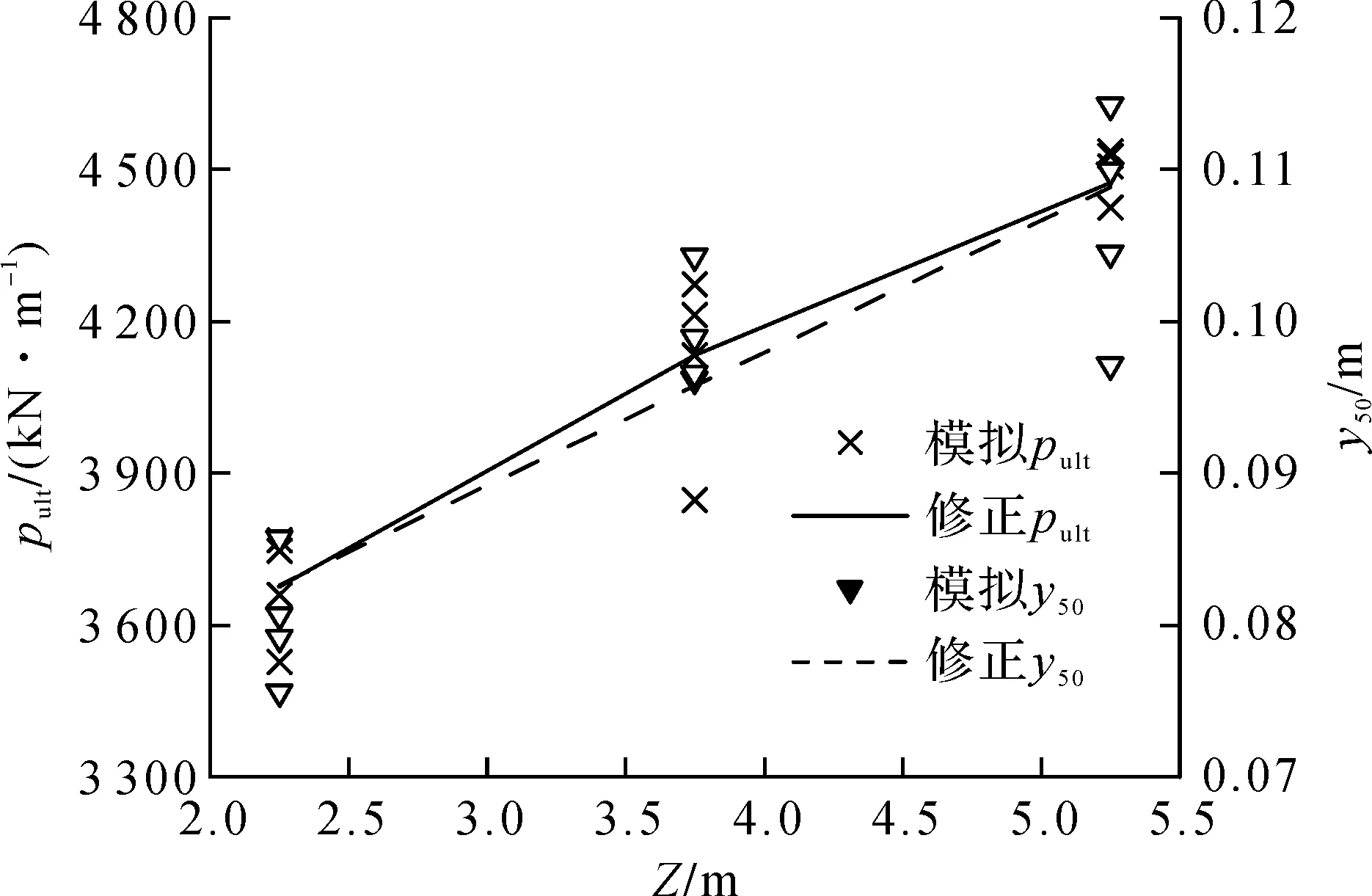
图7 修正后的pult和y50Fig.7 Modified pult and y50

4.3 修正桩身变位特征值y50

桩周土达到水平极限土反力一半时，对应的桩身水平变位为y50，下文称作桩身变位特征值。桩身变位特征值是p—y曲线的另一个重要参数。表7给出了不同桩-筒几何尺寸下数值模拟得到的桩身变位特征值y50。由表7可知：桩身变位特征值与深度z存在线性关系，为此可引入一个与深度z相关的无量纲系数k，重新构造y50，y50和k的计算式分别为

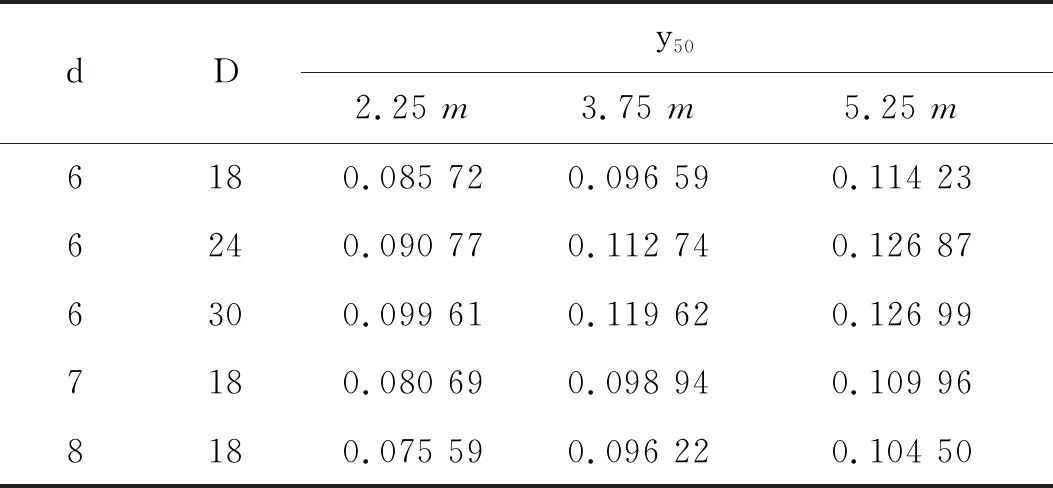
表7 桩体特征位移Table 7 Displacement of pile 单位：m

(7)

采用最小二乘法求解式(7)中待定系数m，n，得到y50修正后公式，即

y50=[0.030(z/h)+0.004]ds

(8)

式中h为筒高。

图7给出了修正后的桩身变位特征值与数值模拟结果的对比，可发现二者较为吻合。

API规范中采用p/pult—y/y50无量纲曲线来反映描述桩土相互作用的p—y曲线，这种曲线形式能更加直观地体现桩身土反力与桩身水平变位之间的关系。根据API规范所给出的计算公式对p/pult—y/y50进行修正是定量分析桩-筒组合基础p—y曲线的有效途径。

将式(1)移项并改写系数，可得

(9)

根据y50的定义以及数值逼近方法，求出待定系数a，b，得到适用于桩-筒组合基础的p—y曲线计算公式，即

(10)

将有限元模拟得到的结果绘制成p/pult—y/y50曲线，如图8所示。由图8可知：桩-筒组合基础的p/pult—y/y50曲线与API规范推荐曲线在未达到水平极限土反力之前都是典型的幂函数分布。有限元模拟结果与API规范完全吻合。API规范曲线达到水平极限土反力时，y/y50值远大于有限元模拟结果，这导致API规范推荐曲线割线斜率与有限元模拟结果差距悬殊。

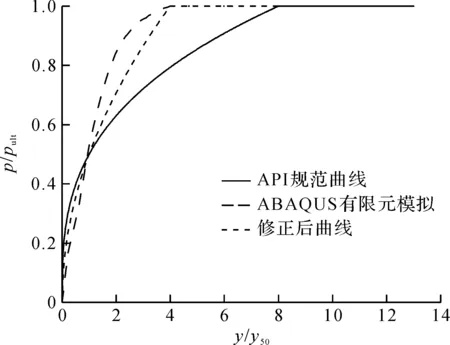
图8 p/pult-y/y50曲线Fig.8 p/pult-y/y50 curve

采用修正后的p—y曲线公式，计算筒径D=18 m的桩-筒组合基础的pult与y50，绘制p/pult—y/y50曲线，并与有限元模拟结果进行对比，如图9所示。由图9可知：p—y曲线修正良好，基本能够正确反映水平荷载作用下桩-筒组合基础水平土反力与桩身水平变位的关系。

图9 修正后p—y曲线Fig.9 Modified p-y curve

5 结 论

笔者采用数值模拟的方式建立了不同几何尺寸下的桩-筒组合基础模型，并通过与大直径单桩基础的对比，从水平承载力、土反力和位移分布等多个角度定量分析了筒体对大直径单桩基础的加固效果；通过修正土体极限土反力、桩身变位特征值，提出了适用于桩-筒组合基础的p—y曲线，得到以下结论：1) 桩-筒组合基础的内力分布与单桩基础规律一致；2) 筒体对桩体有显著的加固效果，通过对基础进行水平加载，可知筒体直径D相较于筒体高度h对加固效果的影响更显著；3) 桩-筒组合基础能更有效地利用3d～5d深度范围内土体的水平土反力，从而提高基础的水平承载能力；4) 在筒体加固范围内，同一深度处桩-筒组合基础水平极限土反力远大于单桩基础，桩身变位特征值y50随深度呈线性变化；5) 对桩-筒组合基础p—y曲线表达式进行修正，得到桩-筒组合基础的p—y曲线，其形式与API规范推荐的单桩基础p—y曲线一致，均为典型的幂函数分布。