载重量变化对矿用车轨迹跟踪影响研究

郑戍华， 乔亚军， 王向周， 李守翔， 陈冬清

(北京理工大学 自动化学院，北京 100081)

随着矿区生产作业活动对提高生产效率、生产作业安全性需求的增长，以及矿用车电子化的普及，矿用车自动驾驶的需求正逐步变为现实. 不同于乘用车的自动驾驶，由于矿用车具有体积、空载质量、载重量都很大的特点且其行驶路况差，使得矿用车自动驾驶的轨迹控制难度很大，解决矿用车的轨迹控制已经成为实现矿用车自动驾驶的技术瓶颈之一.

目前，车辆模型主要有车辆横向、纵向、横摆运动3自由度车辆单轨动力学模型[1]、车辆的侧偏模型[2]、车辆的垂直振动模型[3]等. 单轨动力学模型一般仅考虑平面内的直线运动和圆周运动[4]，而不考虑车辆侧偏和垂直振动，也不考虑载重量对其受力的变化影响；垂直振动和侧偏模型依据车辆的横向和垂直方向转动，考虑车辆的侧倾角和横摆角变化，为车辆安全驾驶提供限制条件，但也没考虑载重量对其限制条件的影响[5]. 乘用车整车质量及质心位置变化不大，这些模型对乘用车具有好的适用性. 但矿用车质量及质心位置变化很大，这些模型难于直接用到矿用车的轨迹控制中.

图1为内蒙古北方重型汽车股份有限公司生产的NTE260型矿用车，该车空载质量达到177103kg，额定载重量达到233103kg，物理尺寸14.4 m(长)8.35 m(宽)7.4 m(高)，后桥4轮电驱动，前桥2轮为被动轮，前桥液压转向. 车上配有柴油发电机，柴油发电机驱动交流发电机发电，整流后送至高压直流母线，经逆变后驱动两后桥牵引电动机，后桥牵引电动机的动力分别经两轮边减速器后驱动车轮产生. 可见，矿用车车辆体积庞大、空载质量大且载重量变化大，这些因素对车辆行驶性能均有很大影响. 因此，针对该车型，本文研究载重量及其变化对矿用车的模型及轨迹跟踪控制的影响，建立车辆数学模型，通过仿真研究载重量及其变化大的情况下，矿用车轨迹跟踪控制及其参数优化问题.

图1 NTE260矿车

文中，车辆前进时方向为x轴正向，后桥轴线向左为y轴正向，空载时车辆质心为原点o，垂直xoy平面向上为z轴方向，建立车辆的o-xyz右手坐标系. 其中x轴方向表示纵向，y轴方向表示横向(侧向)，z轴方向表示垂向.

1 考虑整车质量及其变化的侧向力模型

假设车辆质量由6个轮胎均分，则每个轮胎的垂向载荷Fz

Fz=mg/6 000=(m0+m1)g/6 000

(1)

式中：m为车辆总质量；m0为车辆空载质量；m1为车辆载质量.

采用常用魔术轮胎模型[6]计算的侧向力Fc(λ)

Fc(λ)=Dsin{C×

arctan[Bλ-E(Bλ-arctan(Bλ))]}+Sv

(2)

式中：λ=α+Sh，α为轮胎侧偏角，指轮胎前进方向与x轴夹角. 其他参数表达式和意义如表1所示.

表1 魔术轮胎模型中各参数表达式和意义

表中γ为轮胎外倾角，指轮胎垂直方向与z轴夹角.

空载情况下，参数a0～a13取参考文献[6]中的值，轮胎的侧偏角α与其侧向力Fc关系如图2所示. 实际中车辆侧偏角α一般都很小(α≤5°)，从图2可以看出，在这种情况下轮胎侧向力基本呈线性，可按式(3)进行线性化

Fc=Ccα

(3)

式中Cc为整体轮胎的侧偏刚度. 不同载重情况下，套用式(3)计算侧向力会有较大误差. 考虑小角度情况(α≤5°)、计算不同载重量的情况下垂直载荷与侧向力关系，可得图3所示曲线.

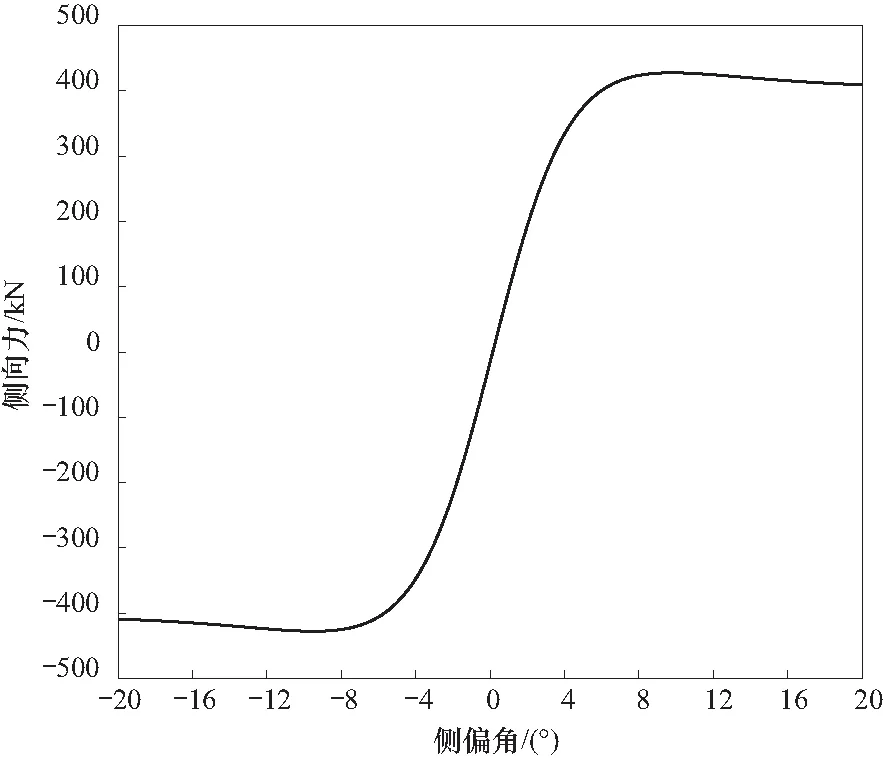
图2 空载下侧偏角与车辆侧向力的关系

图3中，根据侧偏角α及其对应的斜率f(α)，拟合后可得侧向力综合表达式为

Fc=(-0.04α2+0.41α+0.085)(Fz-Fz0)+Ccα

(4)

式中：Fz0为空载时轮胎受到的垂向载荷；Fz-Fz0=m1g/6 000为载重量对垂直载荷的影响. 侧向力Fc与载重质量m1关系为

Fc=(-0.07α2+0.67α+0.11)m1/1 000+Ccα

(5)

可见载重量直接影响轮胎的侧向力，因此，矿用车的轮胎模型线性化简化和汽车模型必须考虑矿用车载重量的影响，文中采用线性化后的式(5)来进行建模.

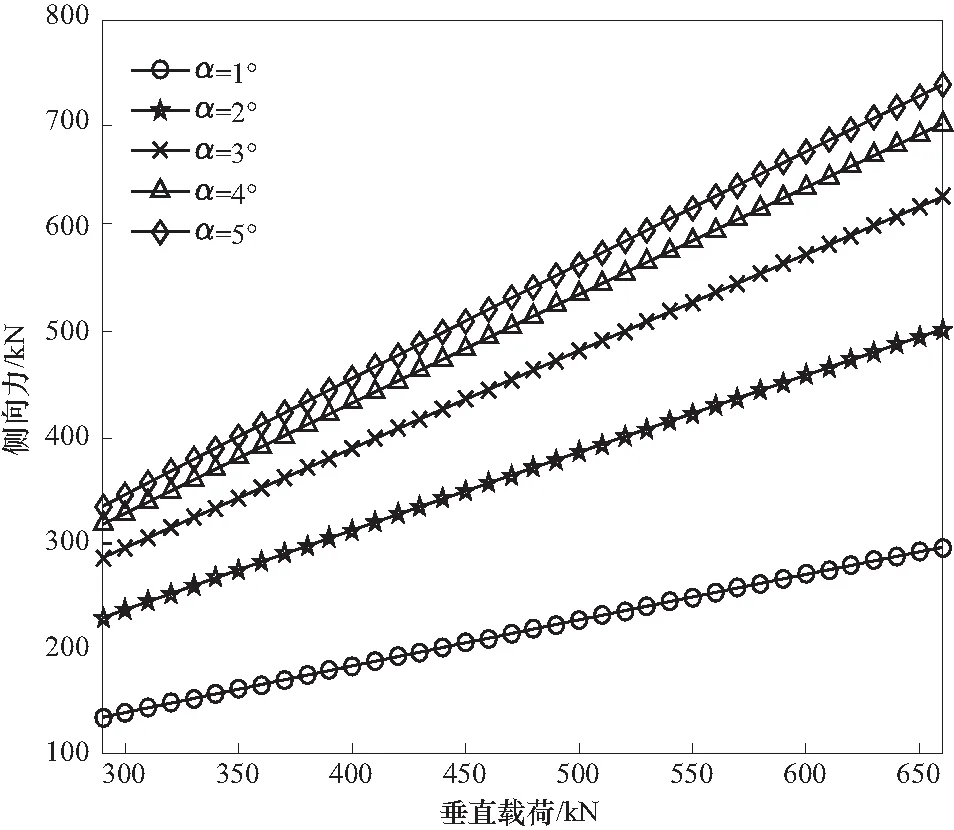
图3 垂直载荷与车辆侧向力的关系

2 矿用车建模

在道路坡度角θ存在且侧偏角在小角度情况下，对车辆进行受力分析，车辆受力模型如图4所示.

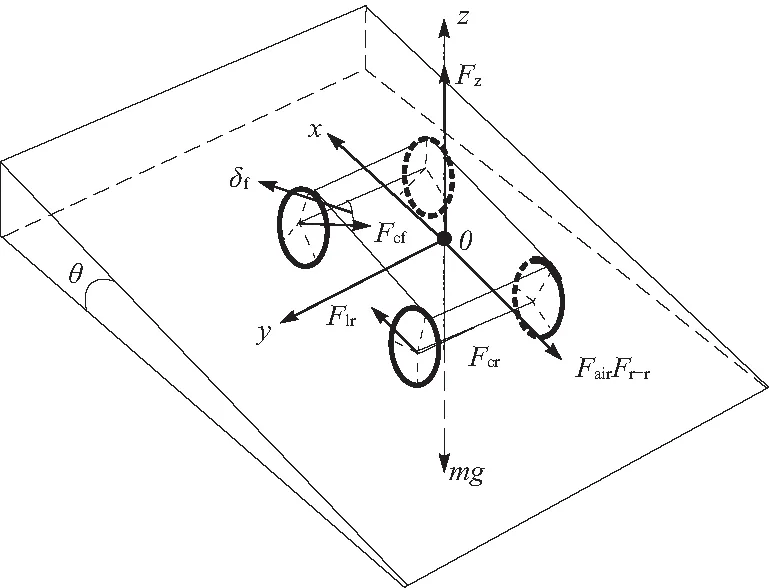
图4 车辆受力图

车辆前后轮侧偏角不同，Fcf，Fcr分别表示车辆前、后轮侧向力，按式(5)计算.

在x轴方向上，考虑空气阻力Fair、滚动阻力Fr_r等，整车受力可表示为

(6)

在y轴方向上，有

(7)

绕z轴转动，有

(8)

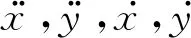
考虑矿用车的质量大、惯性大，将前轮转向角δf与方向盘转角δ关系用惯性环节表示为

(9)

式中：k为转向系统比例常数；T1为转向系统时间常数.

3 车辆整体横纵向控制

仿真过程中，整车的各参数如表2所示.

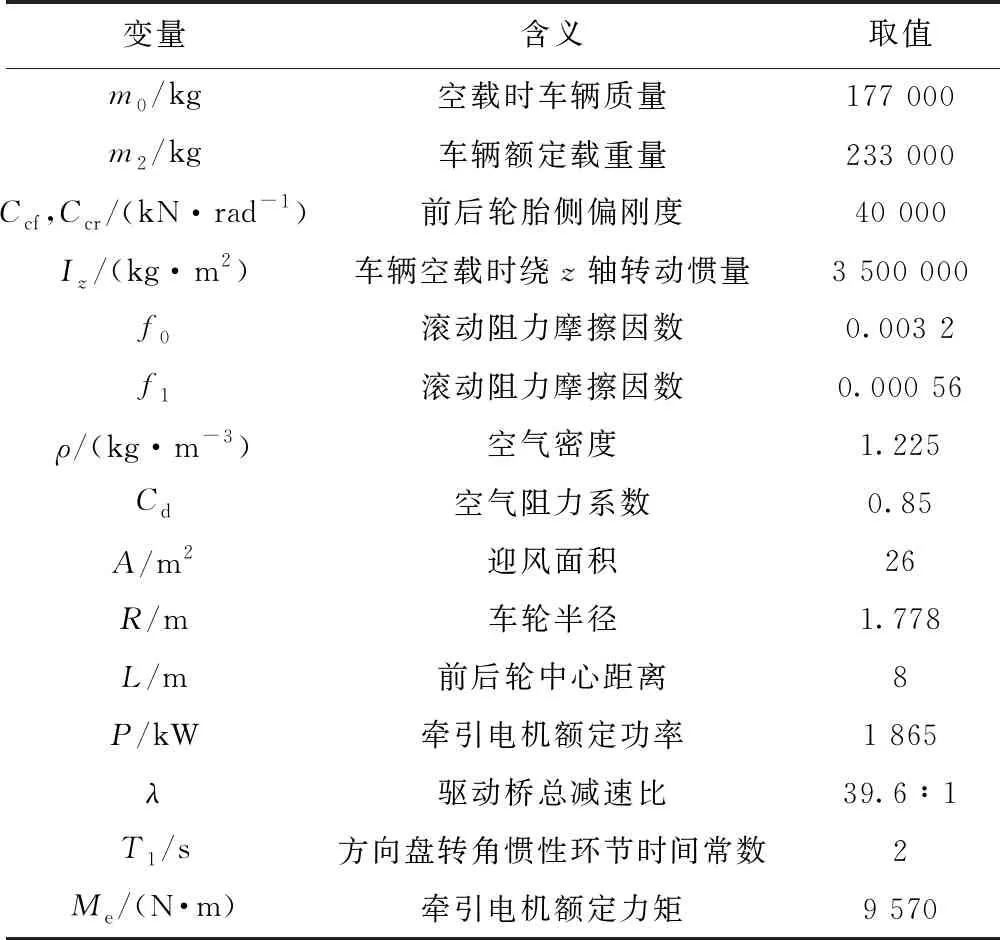
表2 车辆仿真参数取值及其量纲

3.1 车辆的纵向控制

mgsinθ

(10)

式中车辆的纵向作用力Flr是两后桥牵引电动机分别经两轮边减速器后扭矩M在轮胎上产生的驱动力. 假设轮胎与地面之间不存在打滑，式(10)可表示为

mgsinθ

(11)

电机、减速器及电机交流调速系统按惯性环节考虑，期望驱动扭矩Mr与后桥单边驱动扭矩M的关系可表示为

(12)

式中T2为电机及其交流调速系统的时间常数.

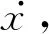
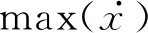
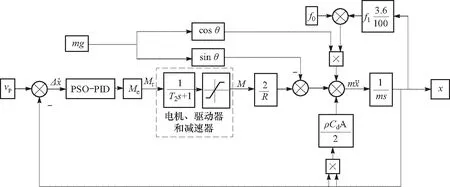
图5 车辆纵向控制结构图

(13)

式中：第1项表示文献[7]中的PID的优化性能指标(ITAE)；第2项表示最大超调量. 两者为纵向控制的优化指标，既体现了跟踪的快速性，又体现了跟踪的准确性. 期望纵向速度为10 m/s、坡度角变化时，不同载重量控制整体效果如图7所示.

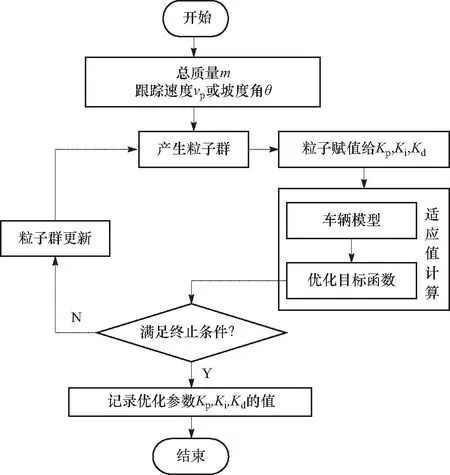
图6 PID参数的 PSO优化流程图

仿真实验结果表明：期望速度为10 m/s时，不同载重量、不同道路坡度情况下均可得到较好的车辆速度跟踪结果. 当道路坡度角突变时，车辆速度会产生扰动，也可较快实现调节.

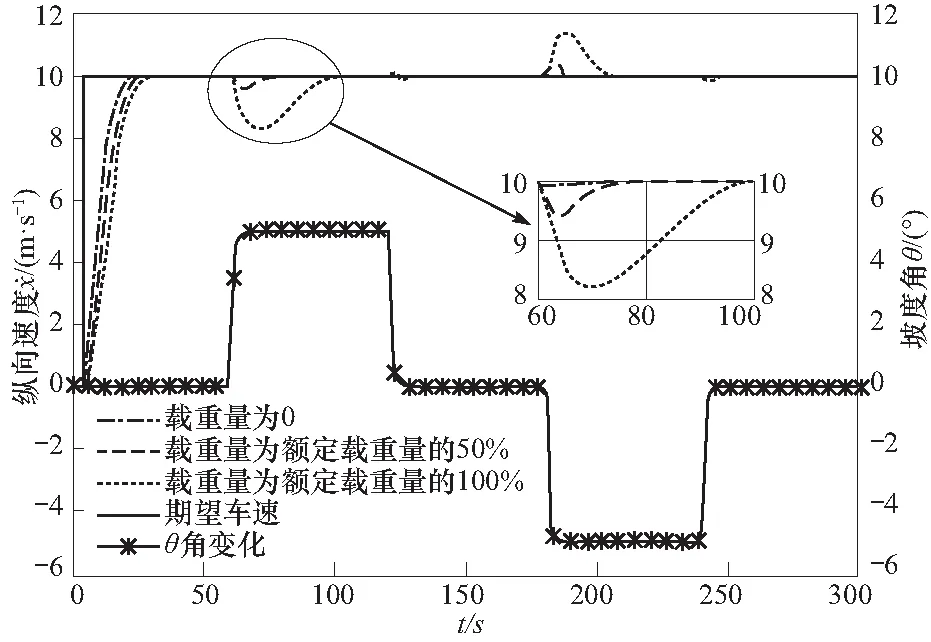
图7 车辆纵向跟踪效果

3.2 车辆的横向控制

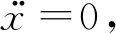
(14)

依据式(14)建立的Simulink模型如图8所示. 系统输入为期望前轮转向角δf_p，输出为实际前轮转向角δf，控制量是通过调节输入车辆的实际转角大小，达到控制车辆前轮转向角，进而控制车辆实际转弯半径，实现车辆按预定半径转弯.

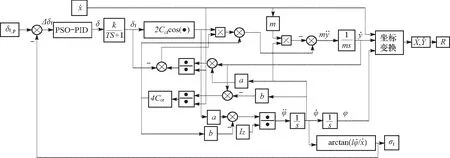
图8 车辆横向控制结构图

与纵向控制流程类似，横向控制PID的PSO优化，输入为载重量，期望的前轮转向角δf_p，输出为方向盘转角δ，终止条件为误差精度或迭代次数. 优化目标函数如式(15)所示

ybest=

(15)

式中：max(e)为跟踪半径的最大误差；max(δf)为跟踪前轮转向角的最大误差. 当期望的前轮转向角为10°时，不同载重量下前轮转向角跟踪效果如图9所示.

仿真实验结果表明：期望前轮转向角为10°时，满载与空载时相比，超调量达到2°，同时跟踪的转弯半径最大误差增加了0.15 m. 车辆载重量越大，整体的惯性越大，前轮转向角上升速度越慢，整体超调越大，跟踪半径误差越大. 因此，不同的载重量情形，需要调节不同的PID参数来进行优化，减少车辆横向跟踪半径的误差，实现车辆横向的轨迹跟踪.

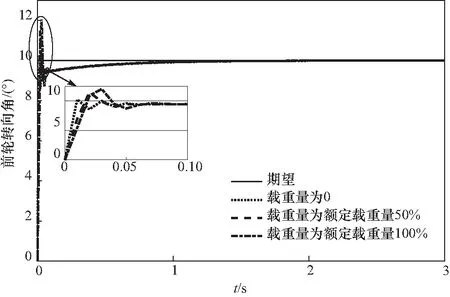
图9 车辆前轮转向角跟踪图

4 仿真研究

采用上述纵、横向运动模型，研究了图10所示轨迹跟踪的控制问题，以(50.0,-45.6)作为起点，经一圈后绕回到起点. 首先，依据车辆当前位置和最优轨迹，确定车辆处于直线段或者曲线段；其次，直线段确定其最优速度以及直线段结束位置，曲线段则计算其转弯半径、车速期望前轮转向角大小；最后，依据车辆载重量确定其最优参数进行相应的轨迹跟踪. 车辆满载行驶，仿真结果如图10所示.

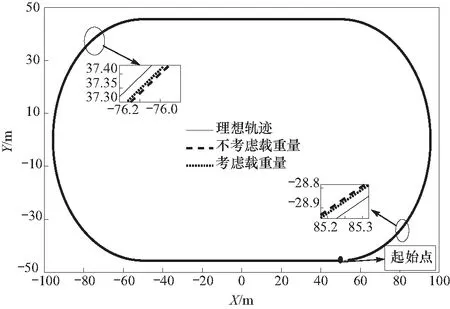
图10 车辆轨迹跟踪图

当车辆载重率从0，50%到100%变化时，不同控制算法车辆整体对轨迹跟踪的最大误差如表3所示.

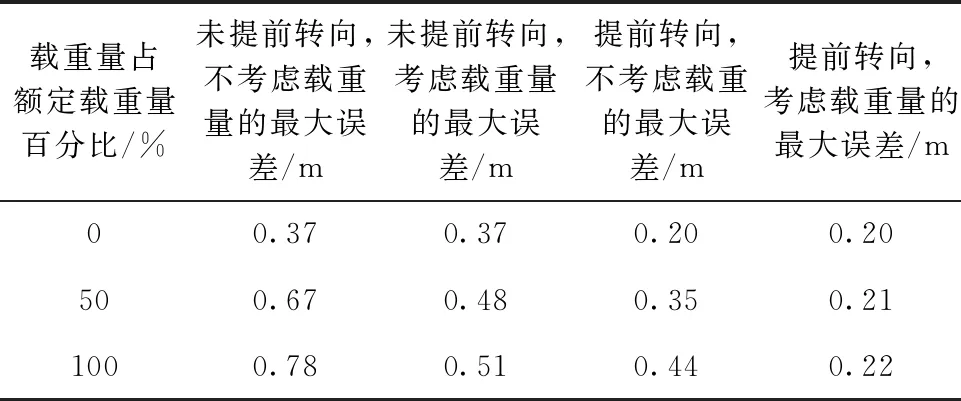
表3 轨迹跟踪最大误差比较

从表3可得：不考虑载重量情况下，车辆的轨迹跟踪最大误差会随着车辆载重量的增加变大，会对整体车辆的安全驾驶产生影响. 考虑提前转向、载重量影响后，车辆的轨迹最大跟踪误差可控制25 cm以内，对实现车辆的自动驾驶具有指导意义.

5 结 论

针对矿用车载重量变化大的特点，分析了不同载重量对轮胎所受侧向力和车辆转向系统的影响，建立了适用于矿用车自动驾驶的整车模型. 通过整体矿用车模型化简，得到相应横、纵向控制模型；采用PSO-PID控制是通过PSO算法寻找优化不同载重量下PID参数对应的最小的轨迹跟踪横、纵向误差；通过加入提前转向，模型考虑车辆载重量的影响，实现了减少转弯半径的误差，对实现不同载重量情况下矿用车的轨迹跟踪及自动驾驶具有一定的指导意义.