含水炮孔台阶爆破漏斗试验研究

王 浩，王建国，黄永辉，张智宇,4

(1.昆明理工大学公共安全与应急管理学院，昆明 650093；2.昆明理工大学国土资源与工程学院，昆明 650093；3.昆明理工大学电力工程学院，昆明 650093；4.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室, 昆明 650093)

随着开采深度的不断加深，大气降水及裂隙水堆积、炮孔内积水严重[1]，爆破后大块率高、根底多，原有台阶爆破参数与经验公式法已不再可取。而台阶爆破是露天开采中重要的步骤，台阶爆破的关键因素在于合理的爆破参数。为保障矿山能安全、高效率开采，研究含水炮孔条件下台阶爆破参数已成为解决该问题的关键。诸多学者对含水炮孔爆破展开了较为深入的研究，吴志刚[2]提出水介质耦合钻孔爆破法，通过爆破理论、室内试验、数值模拟相结合对水介质耦合钻孔爆破法进行研究；龚玖等[3]通过理论与室内爆破模型试验，比较了空气不耦合装药和水不耦合装药的能量利用率；姜涛等[4]通过AutoDyn对比炸药爆轰波在空气介质与水介质下对爆破物的冲量大小，分析得出影响装药量的主要因素；雷涛等[5]通过LS-DYNA软件,建立爆破漏斗数值模型分析爆破漏斗成型过程;E.N.Sher等[6]基于脆性破坏理论建立了从爆炸中心向自由面扩展的动态计算模型；虽然部分学者[7-9]论证了水介质的优点，成功利用水介质能有效传递能量以及不可压缩的特性，证明水介质用于爆破的可行性，但露天台阶的爆破漏斗试验研究则多以干孔为主[10-14]，且多以数值模拟、模型试验方法研究为主。

但数值模拟过于理想化，所得到的结果与实际工程应用存在一定误差；模型试验[15]则受限于模型尺寸效应，会直接影响到试验结果的准确性。故作者以晋宁磷矿九号坑为背景，在现场开展特定的水孔爆破漏斗试验，获得水孔装药条件下的台阶爆破优化参数，以此改善露天矿含水炮孔爆破效果。

1 爆破漏斗理论

上世纪50年代，美国矿业学院利文斯顿(C.W. Livingston)通过不同种类围岩的爆破漏斗试验研究，发现一次爆破作用于围岩的能量取决于岩体性质、炸药性能、药包大小和药包埋深等因素,并以此提出了以能量平衡为准则的爆破漏斗理论[16]。当药包埋置在地表以下足够深时，炸药所产生的能量作用于底部岩石中产生弹性变形破坏，无法对地表岩石造成破坏。若改变药包埋置深度至足以使地表岩石发生破坏但未形成明显漏斗，此时炸药的埋深称为临界埋深。当炸药量不变，继续减小药包埋深，药包上方岩石呈冲击式破坏，漏斗体积逐渐增大。当爆破漏斗体积增至最大时，冲击式破坏的上限与炸药能量最佳利用点吻合，此时炸药埋深即为最佳埋深。若继续减小埋深，爆破能量超出此埋深最佳破坏效应所需能量，漏斗体积减小。

利文斯顿弹性变形方程，即：

(1)

(2)

式中:Le为药包临界埋置深度，m；Eb为弹性变形系数；Q0为药包质量，kg；Lj为药包最佳埋置深度，m；Δ0为最佳埋深比,Δ0=Lj/Le，特定岩石种类其Δ0为实数。

2 爆破漏斗试验

2.1 试验准备

试验地点选在岩体节理裂隙发育、积水较为集中的九号坑中部2120平台。试验选用山特维克φ150钻机，6 m长带有刻度的木棍以及5 m长卷尺一把，配喷漆，标记纸等。试验与爆破施工采用1#岩石乳化炸药，其具体参数如表1所示。

表1 1#号岩石乳化炸药参数

2.2 试验方案

首先进行单孔爆破漏斗试验，相同药量条件下起爆不同埋置深度L的炸药，寻找最佳炸药埋深Lj与最佳半径Rmax；然后基于单孔爆破漏斗试验所确定的最佳炸药埋深，进行变孔距同段爆破试验，确定最佳孔底距离d，利用布洛伯格相似法则[17]计算实际爆破作业最佳孔底距a及炸药单耗q。最后在不同台阶斜面倾角下，采用单孔连续柱状装药，根据斜面台阶最小抵抗线W变化特征，分析确定台阶爆破试验最小抵抗线。

2.3 试验结果统计

爆破后清理漏斗口附近碎岩，使用喷漆圈定漏斗轮廓，确定并标记炮孔圆心，按60°间隔量取6个不同角度的漏斗半径，取平均值即为该漏斗的试验半径。选取漏斗底点为笛卡尔坐标系中心点，建立三维直角坐标系，测量爆破漏斗口及内壁若干点的相对坐标，将测量三维坐标带入3Dmine数字化矿山软件，生成漏斗模型，计算漏斗体积[18]。爆破漏斗试验数据采集与体积计算如图1所示。

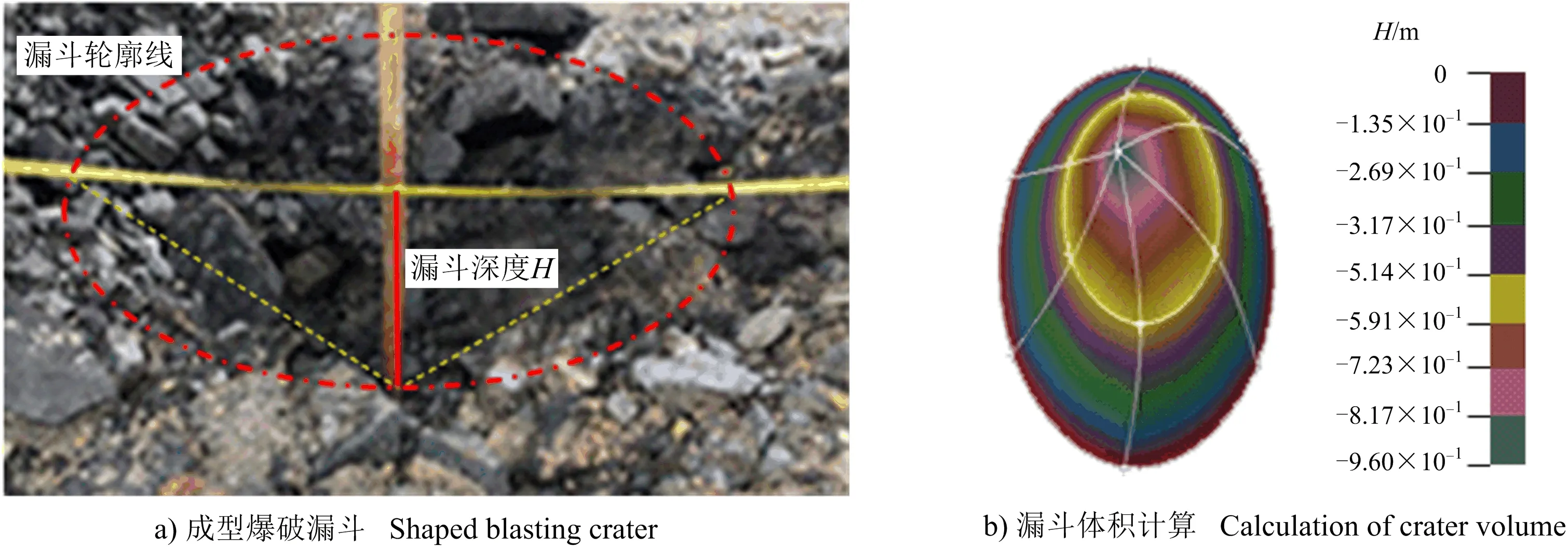
图1 爆破漏斗试验数据采集与体积计算

3 爆破漏斗试验分析

3.1 炮孔深度影响

为保证单孔爆破漏斗试验结果的准确性，试验选用与实际爆破漏斗相同的孔径150 mm。试验选用1#岩石乳化炸药，线装药密度10 kg/m，单孔装药2 kg，为避免孔内水导致药包浮动，将药包固定在内径为110 mm的PVC管内。设计孔深0.9～2.0 m，共计12个孔，各孔试验结果如表2所示，每孔均为自然满水状态。为减少应力波叠加对相邻炮孔爆破漏斗成型的影响，起爆方式为逐孔起爆，设计相邻炮孔间距为5 m。

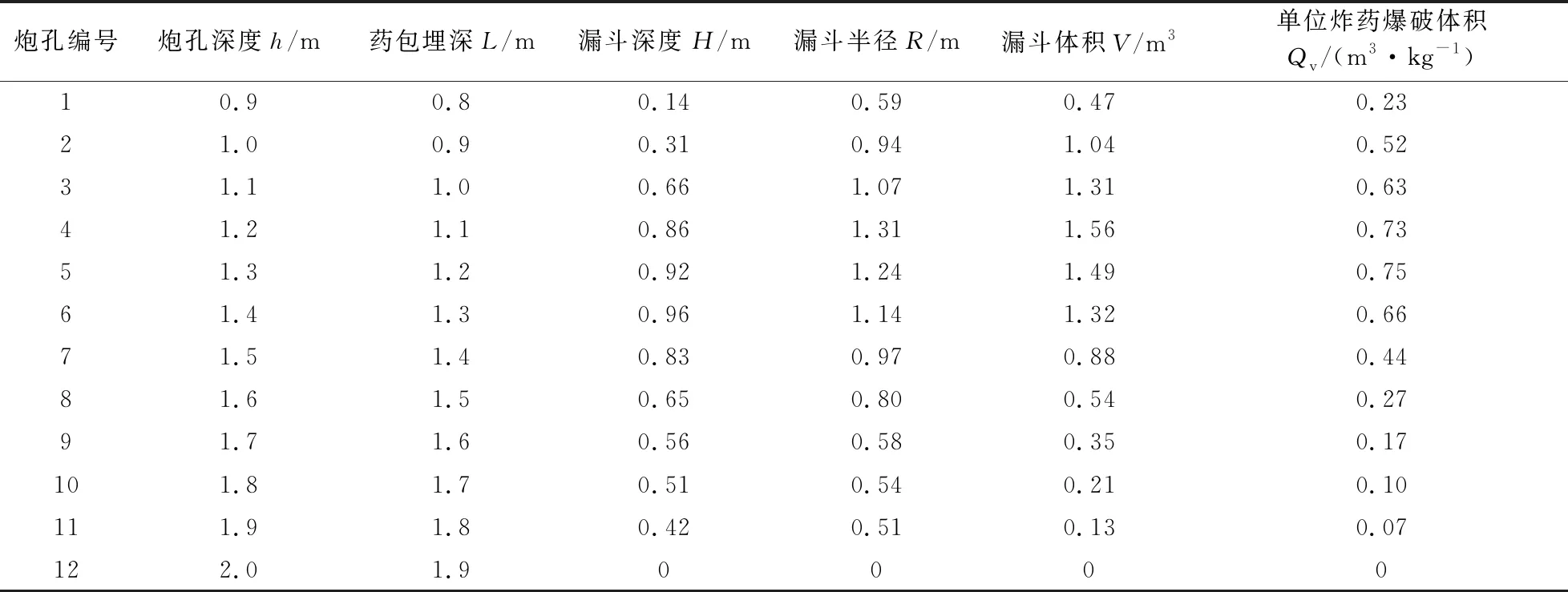
表2 水介质单孔爆破漏斗试验结果

根据表2数据，绘制出药包埋置深度与爆破漏斗半径关系的拟合曲线(见图2)；单位炸药爆破体积特征曲线如图3所示。

图2 漏斗半径与药包埋深关系

图3 单位炸药爆破漏斗体积与药包埋深关系

通过图3可得到药包埋深0.8～1.9 m时，单位炸药爆破漏斗体积与药包埋深拟合曲线呈中间高两端低的形状，爆破漏斗体积变化以L=1.1 m为转折点，当药包位于最佳埋深时，峰值点达到冲击破裂带上限，药包能量利用率最高，所形成的爆破漏斗体积最大；图2拟合曲线趋势与图3相同，在药包埋深L=1.1 m时得最大爆破漏斗半径值，得出最大半径对应药包埋置深度与最大漏斗体积药包埋置深度相吻合。由图2、图3可得出单孔爆破漏斗试验结果为:Lj=1.1 m、Le=1.8 m、Vmax=1.56 m3、Rmax=1.31 m、Δ0=0.57；根据公式(1)得岩体变形能系数为Eb=1.35。依据布洛伯格相似法则变形公式(3)得到孔深为1.2 m条件下实际单孔药量为5.08 kg。实际生产中炮孔深度h=10 m，考虑压榨系数1.42，换算后现场装药量为60 kg。

(3)

式中：r1为单孔爆破漏斗试验药包半径，55 mm；r2为实际生产药包半径，75 mm；Q1、Q2分别为单孔爆破漏斗试验药量、孔深为1.2 m条件实际单孔药量。

3.2 变孔距试验

基于单孔系列爆破漏斗试验确定的最佳药包埋置深度，在九号坑中部2120平台布置5组不同孔距试验组，试验设计孔距为上述试验中最佳漏斗半径的1.5、1.75、2.0、2.25、2.5倍进行取值[19]，得到试验孔间距分别为1.8、2.1、2.4、2.7、3.0 m，试验组间距为10 m，炮孔内为满水状态，各孔内装填2 kg由内径110 mm PVC管固定的1#岩石乳化炸药，起爆方式为同段齐发。炮孔布置如图4所示，爆破后试验结果如表3所示。

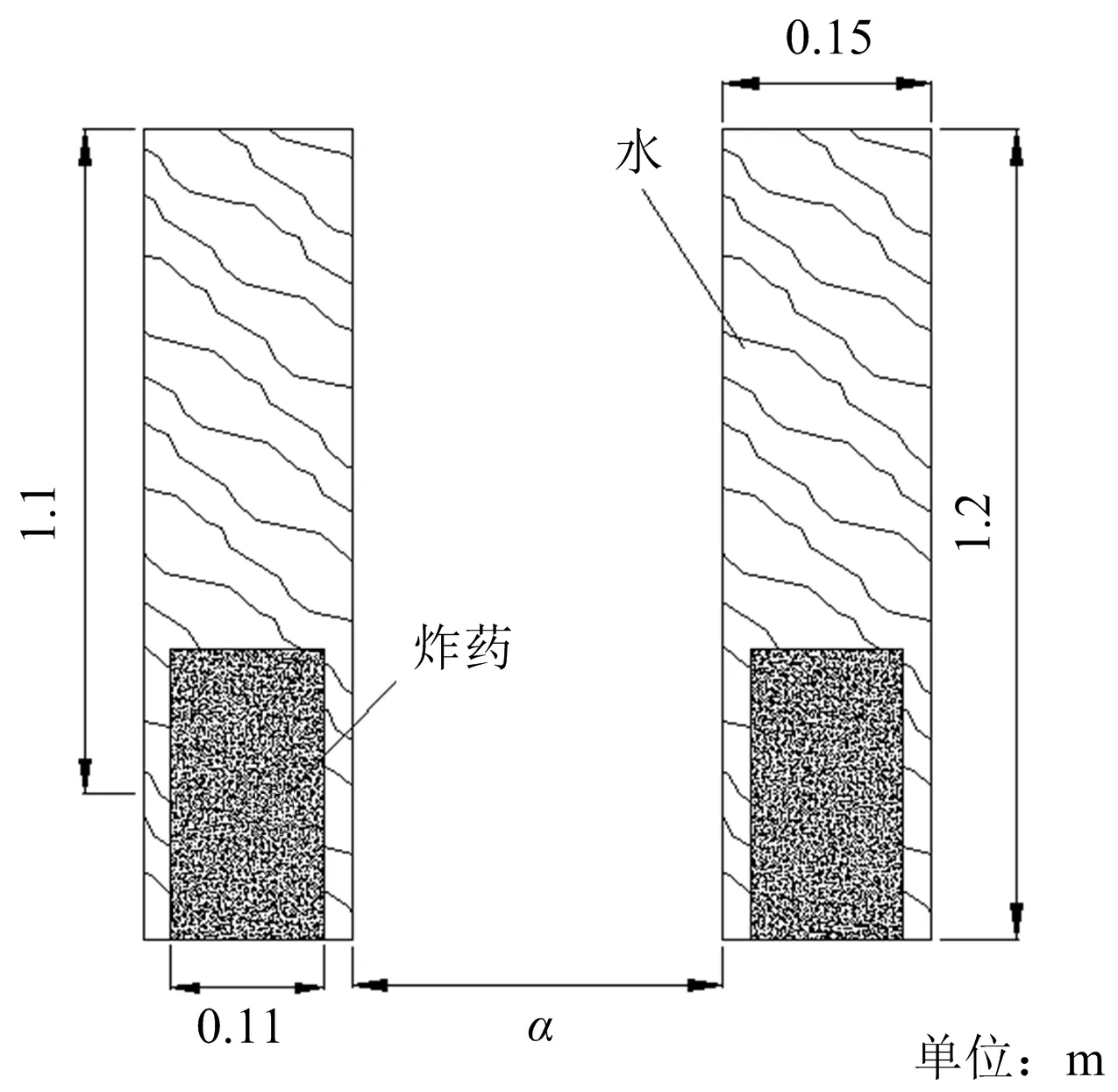
图4 变孔距同段爆破炮孔布置

表3 变孔距爆破漏斗试验结果

由图4可知，孔距α=2.7、3.0 m的2组炮孔爆破后，炮孔间存在明显脊柱隔断，爆破漏斗之间相互独立且未连接成槽；孔距α=1.8、2.1、2.4 m的3组炮孔爆破后沿炮孔中心线贯穿连接成槽，统计有效爆破漏斗体积，得此次爆破最大贯穿沟槽体积的炸药单耗q=0.32 kg/m3。试验结果表明：当孔间距α≤2.4 m的3组炮孔爆破时，相邻水孔爆破漏斗间有明显贯穿现象，相邻爆破漏斗重合较好，爆炸应力波有效叠加作用于岩石，即爆破漏斗最佳孔距α=1.8～2.4 m。依据变形布洛伯格相似法则公式(4)换算得到试适用实际生产孔距a=5.6～7.4 m。

(4)

式中：α、a分别为变孔距爆破漏斗试验孔距、实际生产孔距，m；Q1、Q2分别为变孔距爆破漏斗试验药量、实际生产药量。

图5 水介质变孔距爆破漏斗效果

3.3 斜面台阶试验

根据采场实际台阶斜面倾角范围，确定试验台阶斜面倾角分别为40°与50°，斜面台阶爆破炮孔布置如图6所示，孔口抵抗线0.3 m，设计炮孔深度5 m，装入加工后1#岩石乳化炸药20 kg，装药长度为2 m，炮孔内均为满水状态。

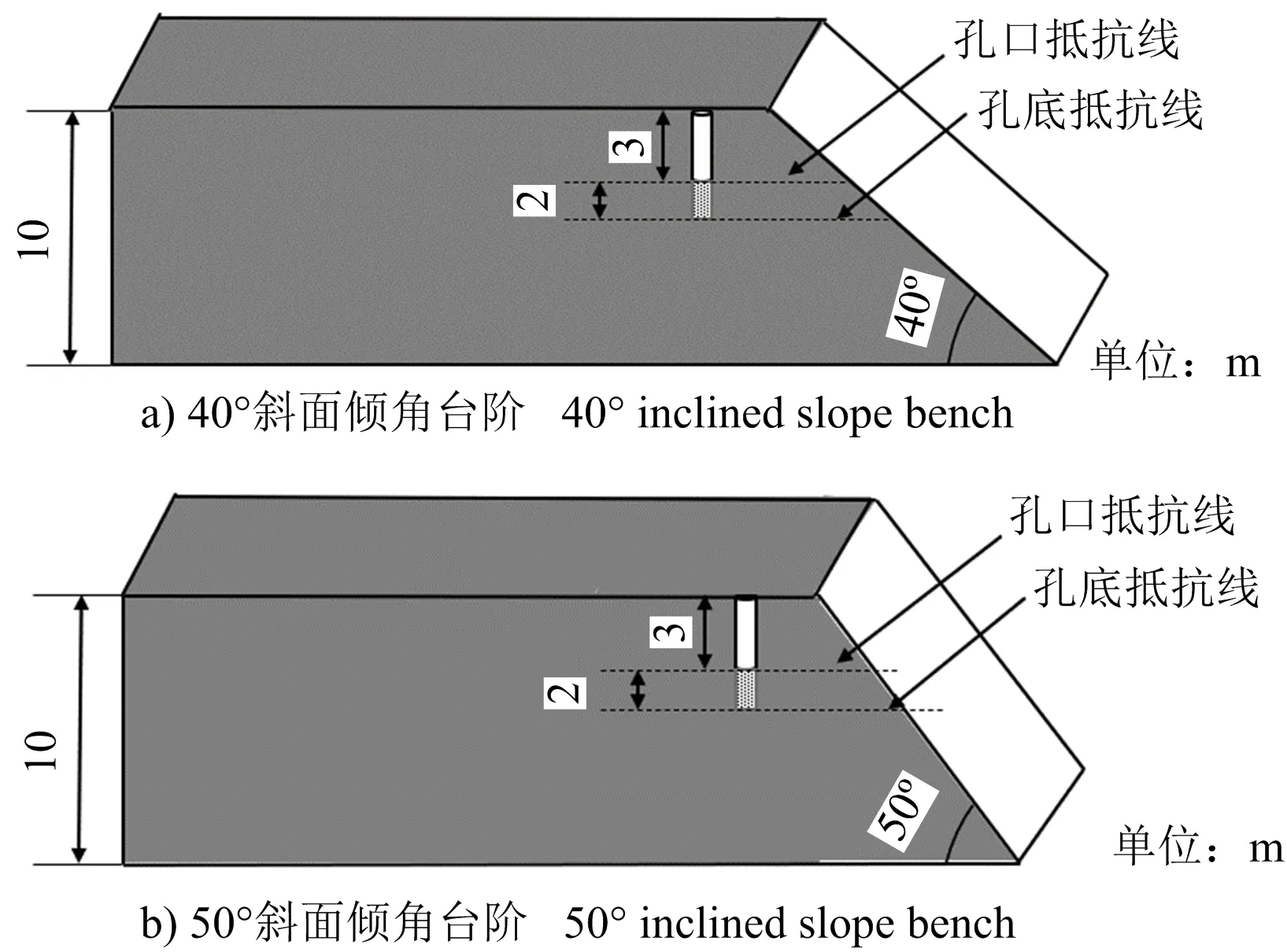
图6 试验炮孔布置

2组试验爆破后岩石块度均匀、大块岩石较少(见图7)，符合试验要求，40°与50°台阶斜面所得爆破漏斗深度分别为2.7、2.9 m，由于岩石破碎、抛掷主导方向沿最小抵抗线方向，此方向应力波最先达到自由面对岩石产生破坏，得到水孔爆破漏斗最佳抵抗线W=2.7～2.9 m。依据布洛伯格相似准则式(5)得用于实际生产最佳排距b=3.9～4.2 m。

图7 台阶爆破试验效果

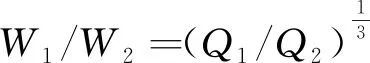
(5)

式中：W1、W2为水孔斜面台阶试验抵抗线与实际生产最小抵抗线，m；Q1、Q2为水孔斜面台阶试验药量与实际生产药量。

4 台阶爆破应用

经相似定律换算后露天台阶水孔爆破最优参数为，孔距a=6 m，排距b=4 m，单孔药量60 kg。根据系列含水炮孔爆破漏斗试验换算结果，在孔内积水严重的九号坑中部2120平台进行现场爆破试验，台阶高度10 m，选用1#岩石乳化炸药，炮孔深度10 m，孔径为150 mm，装药高度4 m，装药方式为耦合装药。参数改进后爆破效果与改进前爆破效果对比如图8所示，可见试验爆破效果良好。为了量化改进后的爆破效果，统计反应爆破效果的相关指标，参数如表4所示，研究分析发现大块率较改进前下降20.6%，块度适中，爆堆松散程度良好，炸药单耗由原先的0.33 kg/m3下降至0.25 kg/m3，采场开采成本降低、开采能力提高，矿山经济效应得到明显改善。

图8 爆破前后效果对比

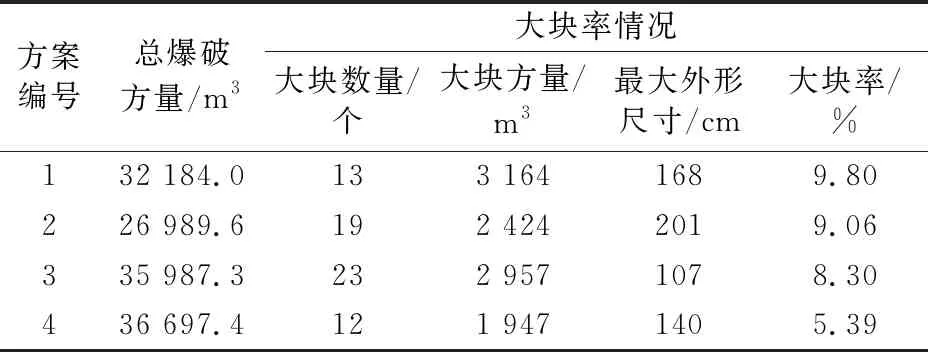
表4 现场试验结果

5 结论

1)针对晋宁磷矿炮孔积水情况，选取2120平台开展孔内满水条件下单孔爆破漏斗试验得到炸药临界埋置深度、最佳埋置深度、最佳埋深比、弹性变形能系数；将以上所得数据分别应用于变孔距爆破漏斗试验、斜面台阶爆破试验得到合理孔距、排距范围值。将试验参数换算后可以用于指导矿山生产。

2)将优化后爆破参数应用于现场爆破工程，统计分析发现大块率较改进前下降20.6%，爆堆松散程度良好，块度适中，炸药单耗由原先的0.33 kg/m3下降至0.25 kg/m3。