网络匿名度量研究综述*
赵 蕙,王良民,申屠浩,黄 磊,倪晓铃
1(江苏大学 计算机科学与通信工程学院,江苏 镇江 212013)
2(江苏省工业网络安全技术重点实验室(江苏大学),江苏 镇江 212013)
互联网用户的隐私数据越来越容易受到各种商业或其他用途的掠夺,用户数据可能面临广泛的监控,可能被商业公司收集和出售,可能由于网络攻击而泄露[1].面对通信网络中存在的重大隐私风险,仅仅通过消息加密提供内容的机密性是远远不够的,通过流量追踪技术,攻击者可以揭示流量发送者和接收者之间的通信联系等大量信息[2],例如谁发送了信息、谁接收了信息、谁在与谁通信、何时通信、通信频率等.保护网络空间隐私的愿望推动了匿名通信系统的设计,使得用户可以在使用互联网服务时,隐藏通信终端主机的身份和通信关系等隐私敏感信息.近年来,匿名通信系统已从小范围部署发展成为数百万人使用的大众市场软件[3],Tor、I2P、Freenet、ZeroNet 等都是被广泛使用的匿名通信系统[4].
随着网络匿名通信系统设计的迅速发展,对匿名系统进行有效的评估也需要开展更广泛和深入的研究.针对网络匿名通信系统的研究工作在部署成本、路由性能、拥塞控制、可伸缩性和安全性等方面不断改进[1,5],这些方面也是匿名系统评估的主要角度,安全性是其中关键性的指标.一个匿名通信系统可以从匿名性、抗跟踪性、抗封锁性、抗窃听性、鲁棒性和可用性等不同角度进行评价[6],其中,对匿名通信系统所能提供的匿名程度的量化,即匿名度量,是对这类系统进行度量的重点和关键.因此,如何对不同的匿名通信系统所能提供的匿名性的程度进行评估和量化,是一个重要的研究问题,是匿名领域新的研究焦点.对匿名通信系统的用户而言,匿名度量的结果表明系统面对各种攻击场景能为用户提供多少匿名性:估计过高,用户可能会被置于无法预测和接受的风险之中;估计过低,会导致用户在不必要的情况下放弃使用系统.对匿名通信系统的开发者而言,匿名度量可对不同匿名需求下设计和改进匿名通信系统提供客观和科学的依据,也有利于对不同的匿名通信系统进行对比.但是如何权衡与比较自己研究的新系统和新机制,成为一个比较困扰匿名系统研究工作的难题.当前,研究匿名机制的文献有很多,但却缺乏统一的匿名机制模型和攻击模型.本文的综述内容主要是面对有关匿名机制的研究者,通过全面介绍匿名度量方法,为进行匿名设计的研究者在选择合适的匿名度量方法方面提供一点线索,进一步地,使研究者能够根据所设计的匿名机制,适当改进和拓展匿名度量方法.
匿名度量是隐私度量[7]在匿名通信领域中的研究.IEEE 术语标准辞典[8]给出:度量是对一个系统、组件或过程具有的某种给定属性的度的定量测量.本文给出一个匿名度量研究的通用框架,如图1 所示.

Fig.1 A general framework for anonymous metrics research图1 匿名度量研究的通用框架
网络匿名系统的参与实体包括用户、攻击者、匿名网络基础设施提供者.用户实体,例如需要保护机密或敏感业务采购模式的商业公司、需要隐藏身份的记者、犯罪检举者、病人等敏感社会团体以及浏览敏感信息的普通用户等;攻击者实体,例如商业黑客、网络供应商、网络审查和执法机构等;匿名基础设施提供者,例如匿名系统的维护或提供匿名节点的志愿者.用户使用网络产生的网络通信中的原始数据,包括消息的内容和用于消息路由的元数据.攻击者捕获到消息的内容可能会分析出用户的身份信息、浏览兴趣、生活习惯和聊天内容.攻击者捕获到消息的元数据可以分析出包括源地址、目的地址、消息长度等,进而推断用户的身份、通信双方的地理位置和通信关系.
网络中的原始消息由匿名基础设备提供者使用匿名技术处理后成为匿名消息,消息的内容可以通过数据加密算法和数据隐私技术来保护隐私,消息的元数据可以通过加密、隧道、随机化等匿名通信技术来实现隐藏.匿名通信技术的有效性依赖于加密的方法、匿名用户的数量、消息路由的机制、敌手的知识和能力以及网络环境等.匿名后的数据可能被网络中的攻击者观察和分析,攻击者再结合挖掘到的公共信息和用户资料,构成背景知识,从而有可能推测和还原出原始数据.拥有的背景知识越多,对匿名数据成功去匿名化的可能性越大.匿名度量方法依赖于不同类型的输入来计算度量值,经过匿名技术处理的可观察数据和攻击者的背景知识,都可以是匿名度量的输入数据,输入数据的可用性和适当的假设决定了是否可以在给定的场景中使用度量.根据不同指标计算出的能够量化匿名强度的数值,推动不同匿名技术之间的分析和对比,促进匿名技术的进一步发展.
已有一些文献[3,9-13]较全面和系统地回顾了匿名度量的研究工作,但仍可以从不同角度开展具体而深入的比较和分析工作.本文首先寻找匿名度量的发展脉络和特点,按照时间线回顾基于多种理论和方法的匿名度量标准,梳理后得到如图2 所示的研究发展历程.将匿名度量研究领域的发展历程划分为非正式定义阶段、信息论方法广泛应用阶段、多种度量输出的新方法阶段;然后按照提出的匿名度量发展历程的3 个阶段组织内容,围绕对匿名性的度量领域中关键的研究工作,进一步阐述在这条时间线上推动该领域进展的重要研究工作,结合匿名通信攻击技术,分析与对比不同的匿名度量方法;最后,针对目前新兴网络匿名通信系统带来的机遇与挑战,探讨和展望匿名度量进一步的研究方向.
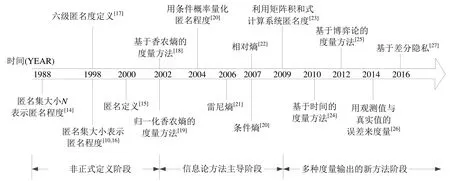
Fig.2 Evolution of anonymity metric research图2 网络匿名度量研究的发展历程
本文第1 节从匿名术语的定义开始,介绍基于匿名集和基于概率的匿名度量方法等匿名度量领域的开创性工作.第2 节围绕信息论的方法,分析香农熵、归一化香农熵、最小熵、雷尼熵、条件熵、相对熵等多种方法对匿名性的度量.第3 节讨论对发送方和接收方关联性进行度量的方法.第4 节从攻击者成功的概率、设计者和攻击者之间的博弈、时间、观测值和真实结果之间的误差、不可区分性和k匿名等多个角度介绍衡量匿名程度的方法.第5 节对多种匿名机制、攻击技术和度量方法进行比较和分析.第6 节讨论信息熵方法在新兴网络匿名通信系统中的应用和Tor 的度量实践,展望匿名度量方法的组合.第7 节总结全文.
1 匿名度量研究的起点
1981 年,Chaum 提出不可追踪邮件问题和Mix 解决方法[14],这是匿名领域的开创性工作.对匿名系统提供的匿名性进行量化,从一开始就是重要的挑战.本节从匿名的定义开始,讨论基于匿名集和基于概率的度量方法,使用的符号见表1.

Table 1 Notation and abbreviation description表1 符号和缩略语说明
1.1 匿名的定义
研究匿名技术的学者对该领域频繁使用的术语有各自的定义和理解,直到2001 年,Pfitzmann 和Hansen 给出匿名性、不可关联性、不可观察性、假名等标准化经典定义[15],这些定义已被大多数匿名文献所采用,图3描绘了4 个非形式化定义在匿名通信网络中的通信环境和通信实体表示.
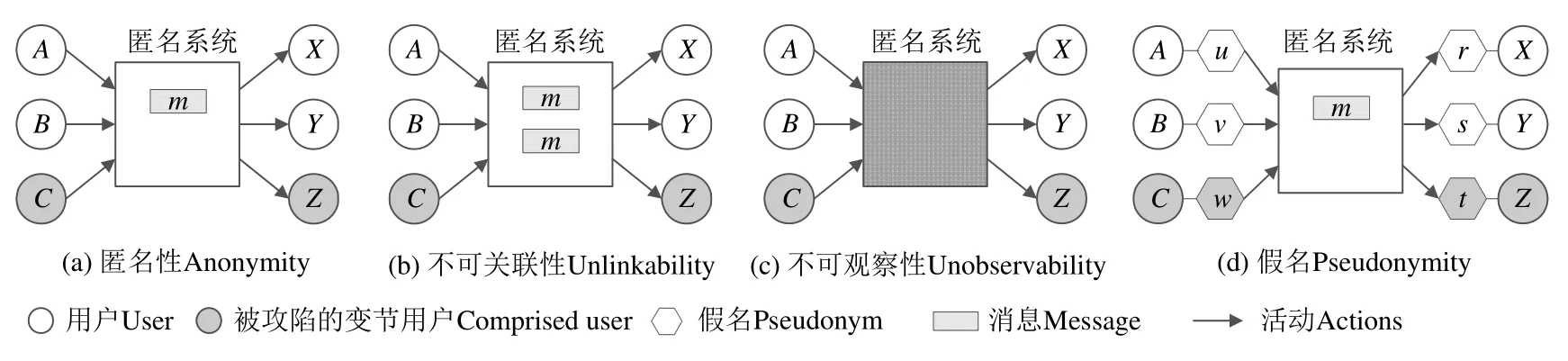
Fig.3 Schematic diagram of anonymous communication图3 匿名通信网络示意图
匿名是借助其他实体的行为来隐藏自己的行为,匿名性(anonymity)被定义为一个通信实体在一个具有相同特性的匿名集中的不可识别性.系统中所有可能参与者的集合是攻击者无法区分的匿名集,是实现匿名的基础.进一步细化匿名集,可能是特定消息发送方的集合称为发送方匿名集,可能是发送方特定消息的收件人的集合称为接收方匿名集,两个匿名集可以是相同的,可以是重叠的,也可以是不相交的,可能随时间而发生变化.如图3(a)所示,系统中的用户为{A,B,C,X,Y,Z},其中,用户C和Z被攻击者攻陷或控制,有效的发送方匿名集为{A,B},接收方匿名集为{X,Y}.
不可关联性(unlinkability)表示攻击者无法判断通信行为之间的相关性.如图3(b)所示,对一个规模为2 的发送方匿名集{A,B},攻击者不能判断两条消息是不是同一个发送者发送,消息由同一个发送者发出的概率是1/2.假设两条消息由不同的发送者发出,攻击者无法关联特定消息的发送方和接收方,即无法区分{A→X,B→Y}和{A→Y,B→X}.
不可观察性(unobservability)表示攻击者无法区分出系统中的消息与随机噪声,不知道有没有消息发送,不知道有没有消息接收,不知道有没有发生消息的交换.如图3(c)所示,意味着攻击者无法区分{A→},{A↛},{B→},{B↛},{→X},{↛X},{→Y},{↛Y}.
使用假名(pesudonymity)标识对象的身份,是实现匿名的一种方法.如图3(d)所示,假设攻击者捕获到通信对{u→s},也不能直接掌握使用身份u和s的真正用户A和Y.不过,随着在系统中交换信息次数的增加和通信时间的增长,假名与真实身份的映射关系会慢慢变得容易分析,假名与真实身份并不必须是一对一映射.也有研究提出使用假名组,用假名集合与身份集合对应,使假名与对象之间具有不可关联性.
除了匿名性,系统的不可关联性、不可观察性和使用假名也隐含反映了系统能够提供的匿名保护,也可以作为度量匿名通信系统的指标.
相比Pfitzmann 和Hansen 在文献[15]中对匿名的概念给出的非形式化的经典定义,基于数学基础,对匿名性、不可链接性等隐私目标进行定义、建模和验证的工作也较早(1996 年)就已开始.匿名的形式化研究有的侧重于用准确的语义来定义匿名性,有的侧重于建模和验证匿名系统.对匿名概念的形式化定义对匿名属性的表达和分析更加清晰和准确,并致力于严格证明匿名协议承诺的安全性,从而更好地量化匿名程度,有利于不同系统之间的比较.我们在第4.7 节展示了面向匿名性、不可关联性等隐私概念开展的形式化定义工作.
1.2 基于匿名集的匿名性度量
根据匿名的定义,特定消息的发送或接收的实体肯定在该匿名集内.文献[16]提出,可以用匿名集的大小来反映系统所能够提供的匿名性:最坏情况下,匿名集为1,意味着无法提供匿名保护;最好情况下,匿名集的大小即网络大小,意味着网络中任何用户都可能是特定消息的发送或接收方.文献[10]对匿名度的定义见公式(1):

其中,N为匿名集中的用户数,可以理解为敌人对匿名性的攻击相当于在猜测一个二进制序列,该序列的长度是对匿名集的大小取以2 为底的对数.从定义上看,匿名的程度取决于用户的数量:随着集合大小的增加,匿名的程度也会增加.当N=1 时,匿名度为0,此时,匿名集中只有一个用户,系统无法提供匿名性;当N=2 时,匿名度为1,此时,匿名集中有两个用户,相当于猜测1 个二进制位的概率,攻击者有50%的机会猜中;当N=64 时,匿名度为6,相当于猜测一个长度为6 的二进制序列.
最理想情况下,匿名通信系统中所有用户被攻击者识别的概率呈均匀分布,即每个用户作为特定消息的发送者或接收者的概率是相等的,匿名度随集合大小的增加而增加,如图4 所示.

Fig.4 Use ASS to compare two uniform systems图4 使用匿名集大小比较均匀分布的两个系统
实际情况中,攻击者可以根据自己掌握的资源和知识,通过流量分析、泛洪攻击等手段,对发送方或接收方做出猜测.这种情况下,个别发送者或接收者被攻击者识别的概率增加,使得系统的匿名性降低.例如,两个系统具有同样大小的匿名集N=3,系统1 呈现均匀分布,如图5(a)所示;系统2 中的一个节点相较其他节点,被攻击者猜测为有更高的概率,是消息发送方,如图5(b)所示.这两种系统的匿名程度事实上有明显差别,但是仅基于匿名集的度量方法无法区别这种情况.
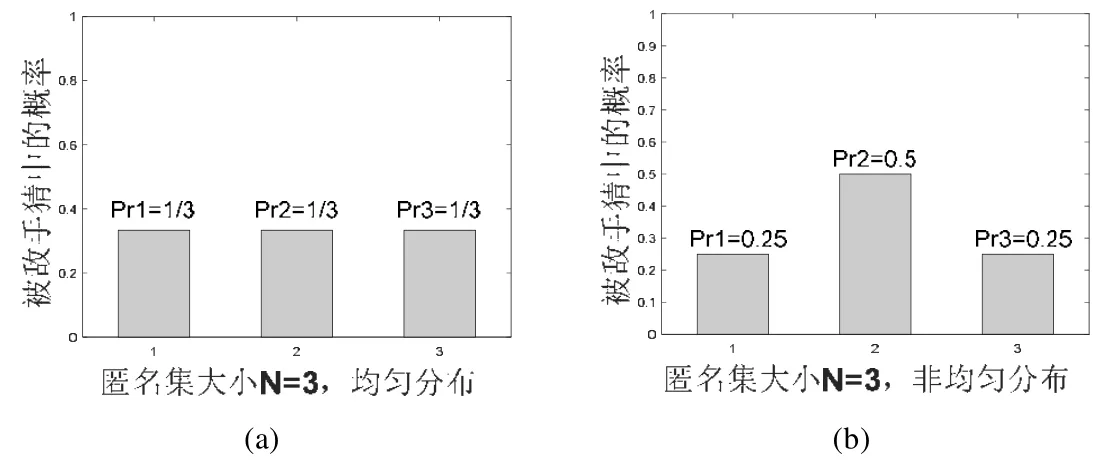
Fig.5 Examples of the systems with different distribution图5 均匀分布系统和非均匀分布系统
因此,基于匿名集表示匿名程度尽管复杂性低、通用性高,但是由于这种方法仅依赖于系统中的用户数量,没有考虑攻击者可能根据先验知识获得的匿名集中每个成员成为潜在目标的概率信息,因此无法区分匿名集大小相同的不同匿名系统.
1.3 基于概率的匿名性度量
考虑到概率分布的不均匀性,假设攻击者对系统中每一个节点分配一个概率,Pri(Pri≠0,∑i∈ASPri=1)表示攻击者识别消息的发送方或接收方的概率.文献[17]从用户角度单独考虑匿名性,从绝对隐私到可证明暴露,提出6 级匿名,见公式(2):

图6 以不同概率分布的匿名系统为例,描绘了6 级匿名.

Fig.6 Six levels of anonymity图6 6 级匿名性划分
对于图6 所示匿名集的大小相同但概率分布不同的两个系统,这种匿名度划分方法可以得到不同的度量值.图6(a)所示对应“无可置疑”,图6(b)所示对应“可能无辜”,判断出图6(a)所示对应着一个匿名性更高的系统.由于考虑到分布的不均匀性,基于概率的方法产生了可区分的度量.
但是,因为不考虑匿名集基数,这种方法并不总能正确地区分出匿名程度.图7(a)所示对应均匀分布的系统,获得“无可置疑”,但匿名集合很小;图7(b)所示对应的系统由于有一个用户的概率稍高于其他用户,获得“可能目标”等级,但匿名集合大得多.
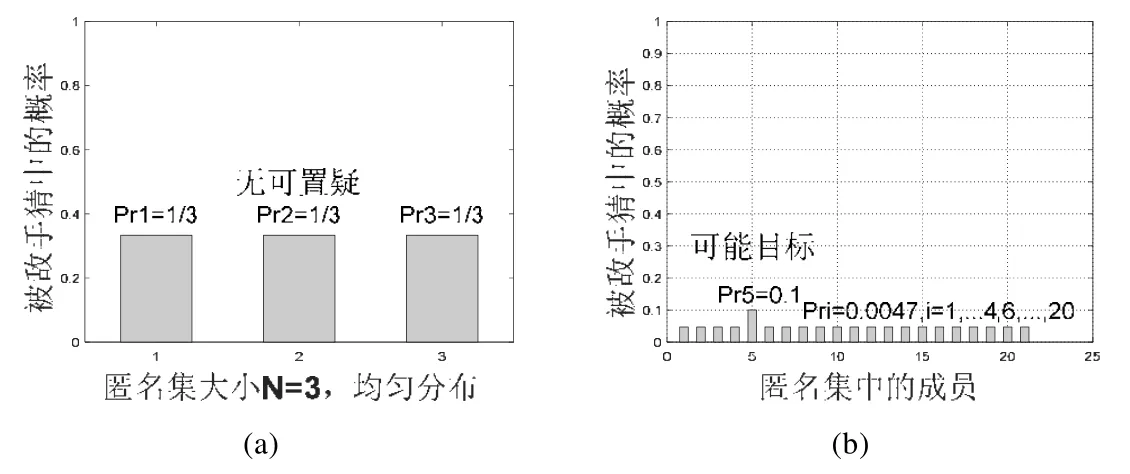
Fig.7 Distinguish incorrectly without cardinality图7 缺乏匿名集基数
尽管均匀分布应该具有更好的匿名性,但是如果匿名集太小,即使系统什么信息也不泄露,攻击者成功识别用户所花费的代价可能也比匿名集大的非均匀分布系统要小得多,攻击者更容易识别,攻陷的成功率更高.因此,这个结果不能反映真正的事实.单独使用匿名集大小或者通信系统中实体被识别的概率来衡量匿名程度存在明显的缺陷,但是它们却非常必要和适合作为度量的输入与其他方法相结合,例如可应用于基于信息论的度量方法中.
2 基于信息熵的匿名性度量
既要考虑匿名集的大小,又要考虑到分布的不均匀性,以及攻击者对网络匿名通信的大多数攻击都能够得到关于相互通信实体的身份的概率信息,因此,当信息理论匿名度量[18,19]被提出之后,即得到了广泛的应用.熵具有很好的统计特性,这些度量方法基于熵,反映了敌手相对于给定消息的发送方或接收方的不确定性.基于信息熵的度量方法对匿名度量的研究有重要的意义,并发展出很多分支.
2.1 香农熵
用信息熵表示系统的匿名程度,见公式(3):

攻击者可能会猜测匿名集中的哪个成员发生了什么样的特定操作,例如谁发送了特定的消息、谁访问了特定的位置,然后攻击者给匿名集中的每一个成员估计一个概率p(x),以表明该目标用户发生特定操作的可能性.例如:攻击者关心的是消息的发送者,那么p(x)就表示目标用户是真正发送者的概率.对p(x)的估计,可以基于贝叶斯推理、随机猜测、先验知识或多种方法的组合,所有成员的概率之和为1.以发送方匿名为例,熵可以直观解释为消息发送者匿名集有效大小的对数.例如,熵为6 的潜在发送方的分布可以解释为:发送方与26-1=63 个其他发送方没有区别.
用基于香农熵的方法量化图7 所示的两个匿名系统.图7(a)所示为获得的匿名程度为ADENT=log23≈1.58,图7(b)所示为ADENT=-(1×0.1×log20.1+19×(0.9/1.9)×log2(0.9/1.9))≈4.29,相比单纯使用概率方法无法正确区分匿名度,信息熵的度量方法得到了较为合理的、能够区分匿名度的量化结果.
下面给出一个香农熵受异常值影响的例子.考虑100 个潜在接收方的分布,除了一个接收方概率为0.109 以外,剩余所有潜在接收方的可能性呈均匀分布,概率为0.009,系统的熵值高达6.40,接近理论最大值log2100≈6.64.因此,假如攻击者能够高概率地识别出目标,剩余大量低概率的成员如果呈均匀分布,则仍然可以导致高熵值,从而表明高匿名度,但此时,熵计算的结果并不符合实际情况.
再如,两个系统匿名程度不同,但熵值相同,如图8 所示.
• 图8(b)中一个节点被攻击者识别的概率为0.5,其余节点呈均匀分布,匿名集大小为101:

两个系统熵值相同,然而图8(b)所示匿名程度事实上低于图8(a).
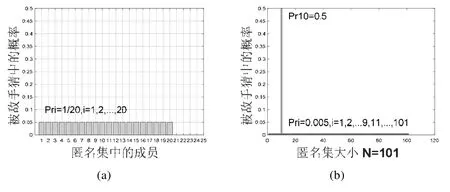
Fig.8 Different anonymity degree with same entropy图8 相同的熵值,不同的匿名程度
2.2 归一化香农熵
文献[19]进一步对香农熵做了规格化的工作,见公式(4),使得表达匿名程度的值被限制在[0,1]的范围内:

用归一化熵可以区分图8 所示场景中的两个系统,图8(a)为ADNENT=4.32/log220=1,图8(b)为ADNENT=4.32/log2101≈0.65,得出不同的归一化熵,从而区分出不同的匿名程度.但在图9 所示的场景中,两个系统的匿名集大小相同、概率分布不同,两个系统的熵都为3.12,归一化熵都为0.72.显然,无论是熵或归一化熵,都无法区分这两个系统.
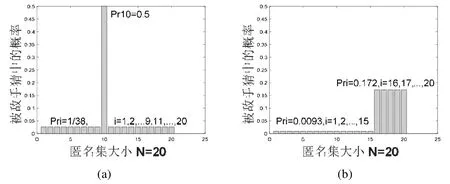
Fig.9 Systems with same entropy and normalized entropy图9 熵相同,归一化熵相同
2.3 最小熵
信息熵的概念提供了随机变量不确定性的度量,考虑的是特定用户的平均情况.针对有着非常薄弱环节的匿名系统,例如有一个用户被识别的概率特别高,攻击者可以通过攻击该用户对系统去匿名化.因此,有文献[11,28]提出用最小熵来计算局部匿名性,从而表示系统最坏的情况,量化出用户可以获得的最小安全,见公式(5):

图9 场景中,可以用最小熵来区分两个系统能够提供的最小安全,计算得到的最小熵分别为1 和2.54.从考虑系统最坏情况来看,图9(b)对应着一个更好的系统.直观来看,如果攻击者资源有限,只能针对一个可能的发送者进行分析,如图9(a)和图9(b)所示系统的识别成功率分别为50%和17.2%.除基本香农信息熵外,还有其他,如雷尼熵[21]、条件熵[20]、相对熵[22]等匿名度量方法.
2.4 雷尼熵
雷尼熵是熵的一般化形式,见如公式(6):

它引入一个额外的参数,香农熵是当参数为1 时的特例;最大熵是雷尼熵当参数为0 时的特例,此时的熵值仅取决于用户的数量,因此是最好的情况,代表了用户理想的匿名性;最小熵是雷尼熵当参数为∞时的特例,这是一个最糟糕的情况,此时的熵值仅取决于攻击者认为概率最高的用户.对于香农熵无法区分的系统,通过调整参数α,雷尼熵可以获得有区分度的结果,如图10 所示.

Fig.10 Different anonymity degree with Rényi entropy图10 不同参数α 的雷尼熵下区分系统匿名程度
2.5 条件熵
考虑攻击者往往结合背景知识进行分析,文献[29]研究用不同路径选择策略下发送方被攻击者识别的概率,以此来表示不同的路径长度和不同的路径拓扑等路径选择策略对发送方匿名的影响.该文讨论了在攻击者掌握一定信息量的条件下,如何利用攻击者算法和消除规则(见第3.2 节),用条件概率和全概率公式计算发送方被识别的概率,其中,X表示随机变量,s表示真正的发送方,F=ω表示攻击者收集到的信息.基于被动攻击模型,攻击者部署若干恶意节点在消息的重路由路径上,恶意节点收集所有通过节点的消息,发现和报告自己的前驱、后继以及消息到达的时间.最后对求得的条件概率计算其信息熵的值,见公式(7):

文献[20]指出:对上述计算条件概率熵值的方法不同于条件熵,条件概率的熵是攻击者根据特定的观察计算不确定性,条件熵计算的是攻击者得到的所有可能的熵之间的加权平均值.条件熵表达式见如公式(8):

其中,随机变量X表示真实的分布,Y描述的是攻击者的观察结果.随机变量X的条件熵衡量的是:如果根据攻击者获得的随机变量Y的特定值,需要多少信息来描述随机变量X.
2.6 相对熵
相对熵(KL 散度DKL)测量两个概率分布之间的距离,给出透露给攻击者的概率信息的数量,表明攻击者的估计与事实有多远.随机变量X表示真实的分布,随机变量Y表示攻击者的估计,Y可能是攻击者的估计值,也可能是攻击者的观测值,见公式(9):
文献[30]提出一种基于相对熵的不可观测性度量方法,从攻击者的威胁模型出发,将匿名通信系统的输入、输出状态映射到一个交互式图灵机,并在此基础上提出一个基于相对熵的不可观测性度量框架,用于度量匿名通信系统的不可观测程度,并给出对Tor 匿名通信系统的传输层插件Meek 和Bridge 度量的实例.
2.7 用熵表示匿名程度的缺陷
表2 汇总了以上提到的匿名方法在各场景下的量化结果,并用符号☑与☒说明是否能够正确区分当前场景下系统的匿名程度.

Table 2 Comparinging different anonymity metrics in different distribution scenes表2 不同场景下的匿名度量比较

Table 2 Comparinging different anonymity metrics in different distribution scenes (Continued)表2 不同场景下的匿名度量比较(续)
表2 中,D1 表示系统1 的概率分布,D2 表示系统2 的概率分布.系统有3 种可能的分布,见公式(10),以下我们称为分布1、分布2 和分布3:

其中,N表示系统匿名集的大小.分布1 表示系统中N个用户之间的概率分布是均匀的,概率为1/N.分布2 表示系统中有1 个用户可能是真实发送方的概率为1/pa,其他用户的概率分布是均匀的,概率为(1-pa)/(N-1).分布3表示匿名集为N的系统中,有2 个子匿名集,真实发送方在这两个子匿名集中的概率分别为pb和1-pb,另一个每个子匿名集内部是均匀分布的,有k个用户属于概率为pb的子匿名集,每一个用户的概率为pb/k,其他用户同属于另一个子匿名集,每一个用户的概率为(1-pb)/(N-k).
两个系统在5 个不同的场景下,比较各自的匿名程度.场景1 设置为将两个都属于均匀分布但匿名集大小不同的系统进行比较,其中,系统1 的匿名集大小为3,系统2 的匿名集大小为20.两个系统都属于分布1.场景2~场景4 中系统1 属于分布1,系统2 属于分布2.场景5 中,系统1 属于分布1,系统2 属于分布3.场景2 设置为两个匿名集大小相同(都为3)但概率分布不同的系统进行比较.场景3 设置为两个匿名集大小不同(3 和20)、分布也不相同的系统进行比较.场景4 设置为两个匿名集显著不同(20 和101)、分布也不相同的系统进行比较,其中一个系统有明显的薄弱点.场景5 设置为两个匿名集大小相同(都为20)的系统进行比较,其中,系统1 有1 个极薄弱点,系统2 有多个薄弱点.
表2 根据匿名度早期文献中的方法,设计场景1 到场景5 的变化来描述一条不同研究之间可能存在的逐渐递进或互为补充的逻辑线索:匿名集的方式可以区分场景1,但无法区分场景2;6 级匿名可以区分场景2,但无法区分场景3;熵可以区分场景3,但无法区分场景4;归一化熵可以区分场景4,但无法区分场景5;最小熵可以区分场景5,但它将所有用户之间的最小匿名度作为整个系统的匿名度,暴露了最薄弱环节,却可能无法捕获整个系统行为.雷尼熵作为一种一般化形式,可以调整参数α的值在不同的场景下获得有区分度的结果.表2 中结果的计算方法可以在第2.1 节~第2.4 节找到.不同方法的组合使用,可对系统的匿名程度给出更完整的表示.例如,熵与最小熵的综合使用,能够帮助反映出系统的平均情况和最坏情况.
尽管计算出熵值有利于系统之间的比较,但是熵易受异常值影响,并不总能提供正确的匿名性.有文献[31,32]认为:即使是熵值明显不同的系统,熵的绝对值本质上并未传达太多比较的意义.熵表示一种全局度量,只和它使用的估计概率一样好.熵回答了系统有多无序,但无法衡量攻击的效果,不能说明攻击者的估计是否准确,也不表示攻击者需要花费多少计算或带宽资源才能成功.作为一种全局度量,它也不能度量特定用户.
考虑两种匿名系统,一个是呈均匀分布的理想系统,另一个是非理想系统,其中有一个节点有较高概率,其余节点均匀分布,用户的概率分布如公式(10)所示的分布1 和分布2.令n1和n2分别表示两个系统的匿名集大小,根据熵的计算公式,如果想达到相同的熵,只需要求解满足公式(11)的匿名集关系:

例如:当pa取0.5 时,只要满足,两个系统就可以获得相同的熵值.表3 给出了具体的计算结果.因此,通过构造匿名系统的分布,非理想系统可以达到任意高的熵值.
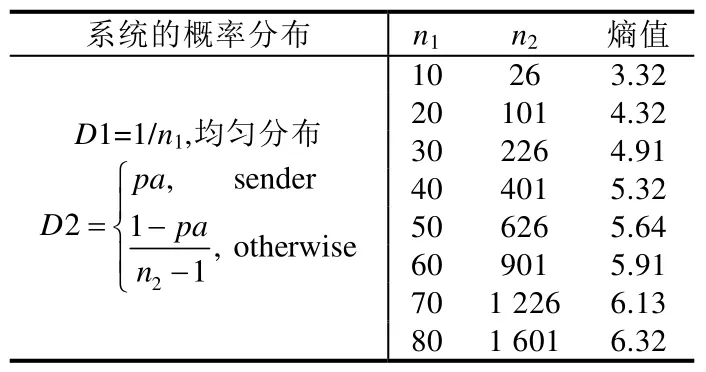
Table 3 Scenes with the same entropy表3 不同分布,相同熵
归一化熵也有相似的缺点[11].考虑两种匿名系统,用户的概率分布如公式(10)中的分布2 和分布3.令n2和n3分别表示两个系统的匿名集大小,k表示系统2 其中一个子匿名集的大小,表示根据熵的计算公式,如果想达到相同的归一化熵,只需求解匿名集和概率关系,具体的求解方法见公式(12):
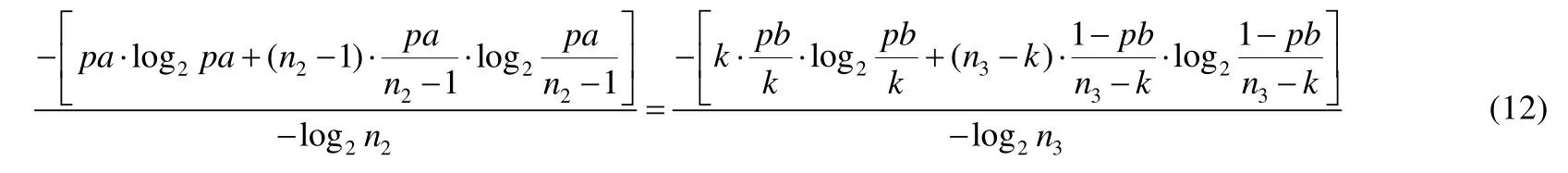
为了简化计算,对公式(12)中的参数取n2=n3,pa=0.5 进行求解,可以得到表4 所示的计算结果.

Table 4 Scenes with the same normalized entropy表4 不同分布,相同归一化熵
信息熵是一种通用性较强的方法,许多研究工作利用熵作为工具对系统的匿名性进行量化计算,从不同对象的角度,我们还可以看到基于熵对关联性进行的度量(见第3.1 节)以及对匿名系统路径匿名和不可观察性的量化(见第6.1 节).
3 发送方和接收方的关联性度量
匿名度量中,发送方(接收方)匿名保证敌人难以确定给定消息的来源,在较多文献中得到阐述.对许多实际的应用而言,关系匿名确保攻击者对于谁与谁正在通信无法追踪,因此,关系匿名是匿名通信系统需要的重要特性.事实上,除了消息的发送方和接收方实体之间的关联外,系统中任意项的关联性都是可以测量的.
3.1 基于信息熵的关联性度量
文献[23]对不可关联性(unlinkability)的概念进行了形式化描述,令M={m1,m2,…,mn}是给定系统中项目的集合,用~r(M)表示在集合M上的等价关联,这个关联把M划分成k个等价类M1,M2,…,Mk,1≤k≤n,对于∀i,j∈{1,…,k},i≠j:Mi∩Mj=∅,M1∪…∪Mk=M,如图11(a)所示的简单的系统模型,描述了一个集合内项目的关联性,根据消息是否属于相同的发送者分成若干等价类,属于相同等价类的消息之间是关联的,表示为(mi~r(M)mj);否则不关联,表示为(mir(M)mj).
然后,该模型被扩展到表示集合之间的不可关联性,如图11(b)所示,对于用户集合U={u1,u2,…,un},消息集合M={m1,m2,…,mn},用(ui~r(U,M)mj)表示用户ui发送了消息mj.

Fig.11 Modeling unlinkability in equivalence图11 利用等价类概念表示关联性
对于随机变量X,P(X=(mi~r(M)mj)表示对于给定的两个项目mi和mj,X取值为(mi~r(M)mj)的概率,P(X=(mir(M)mj)表示mi与mj不相关的概率,满足∀mi,mj∈M,P(mi~r(M)mj)+P(mir(M)mj)=1.
可以使用两个项目的不可关联性来表示对匿名性的影响.对系统提供的(i,j)不可关联性程度,利用信息论方法,设H(i,j):=H(X);对匿名集的成员之间的通信关系分配概率和计算熵值,见公式(13):

文献[28]讨论mix 匿名网络中,关系匿名(relationship anonymity)的定义和计算方法.如图12 所示,考虑一个有N个发送者S1,…,SN和H个目的地D1,…,DH的mix 网络.第i个发送者Si可能正与第j个目的地Dj通信,其中,1≤i≤N,1≤j≤H,因为不同的发送者可能发送不同数量的消息,假设每个发送方Si发送ni条消息msgi1,…,msgini,对于1≤k≤ni,每条消息msgik都有一个目的地Dj.定义[1...H]是潜在目的地的概率分布,[j]为攻击者观察mix 网络后得到的第i个发送者Si发出的第ik条消息msgik,到达第j个目的地Dj的后验概率,利用熵和目的地概率分布,通过计算针对给定一条消息目的地的随机性,来表示匿名程度,见如公式(14):

由于系统可能存在最坏情况,比如其中一个目的地的可能性远远大于其他目的地,因此,文献[28]也提出用最小熵来描述最可能的目的地.
尽管分析的匿名对象不同,但这里对发送方和接收方的关联性进行度量也使用了基于熵值的方法,因此也存在与熵方法同样的局限性.

Fig.12 Relationship anonymity in mix network图12 Mix 系统中的关系匿名性
3.2 基于矩阵积和式的关联性度量
文献[33]提出一种基于矩阵积和式的度量方法,同时考虑匿名通信系统中所有传入和传出的消息,揭示匿名系统中发送者和接收者之间的整体通信模式.如图13(a)所示的匿名通信系统中有4 条消息,它们来自输入集合S={si}和输出集合T={tj},表示这些消息在si时刻进入匿名网络,在tj时刻离开.定义一张二分图G(V1,V2,E),表示输入消息和输出消息的关联,其中,V1=S,V2=T,E代表所有可能的(si,tj)映射的边的集合.设定在这个实时匿名通信系统中,消息mi延迟是有最小时间和最大时间的边界,表示为Δmin≤Δi≤Δmax,例如,Δmin=1,Δmax=4,对于任意的si和tj,只要满足Δmin≤tj-si≤Δmax,就可以在二分图中用一条边来表示它们的关联.例如:对于在s1时刻进入系统的消息,只有可能在t1或者t2时刻离开系统,因为t3和t4时刻不再满足延迟时间边界,从而就可以在二分图中,相应地画出边,构造出的二分图如图13(b)所示.接下来,图G可以用它的邻接A来表示,其中,如果连接si和tj的边存在于G中,则aij为1;不存在,则为0.进而将图G表达成n×n的(0,1)邻接矩阵A,n=|V1|=|V2|,如图13(c)所示.
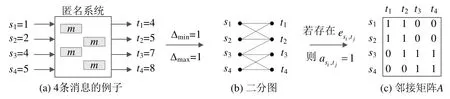
Fig.13 Combinatorial approach to measure relationship between inputs and outputs图13 用矩阵积和式表示关联性
假设在匿名系统中,输入和输出之间存在一对一的关系,即每个发送方和接收方只发送或接收一条消息.如果在G中只有一个两两完美匹配是可能的,那么一个全局攻击者就可以唯一地识别输入和输出之间的关系,因此,系统提供的匿名性为0.当可能存在的完美匹配的数量增加时,攻击者的不确定性也随之增加.为了度量这种不确定性,需要对G中可能的完全匹配数进行计数,这相当于计算邻接矩阵A的积和式per(A),即图G中顶点集合{V1}与{V2}之间两两完美匹配的数量,与计算矩阵A的积和式per(A)是等价的.于是,关联性问题的计算转化成为对矩阵A积和式的计算问题.
攻击者对每个通信关联的估计概率是p(x)=1/Per(A),有研究者将匿名程度定义为公式(15):

对于一个n×n的(0,1)矩阵来说,根据给定的最小时间和最大时间Δmin≤Δi≤Δmax,矩阵的积和式的范围1≤Per(A)≤n!.当系统中只有一对发送方、接收方时,存在最小值、最大值是一个全排列数为n!的完全匹配的情况.此时,A相当于一个全1 的方阵,矩阵的积和式为n!.
相比基于匿名集或基于熵的度量方法侧重从单个用户或单条消息的角度度量系统的匿名性,基于矩阵积和式的度量方法同时考虑了匿名通信系统中传入的消息和传出的消息,计算发送者和接收者之间的关联所需要的信息量,从而提示匿名系统中发送者和接收者之间的整体通信模式,对系统匿名程度有补充表达的作用.文献[34]指出:这种方法不能应对当系统的发送方和接收方进行通信的消息数超过1 条时的场景,应研究能够满足任意数量的消息的更通用的方法.
4 多种输出角度的其他匿名度量方法
匿名度量的不同输入因素,例如,匿名集合的大小、攻击者的不同攻击方法获得的先验知识、匿名系统各自不同的属性特点,都对匿名度量的输出有直接的影响.基于概率的度量方法输出攻击者成功的概率,作为衡量匿名度的指标.基于信息熵的度量方法输出系统的不确定性作为衡量匿名度的指标,随着匿名度量研究的发展,更多的指标被提出以用来衡量系统的匿名程度.
4.1 基于概率分析的攻击者成功率度量
用攻击者成功的概率来度量匿名,是站在攻击者的角度看待匿名系统的评估,本文第1.3 节中提到的6 级匿名方法也可以归于这一类中.对于输出攻击者成功概率或者输出攻击者在大量尝试中成功的百分比[6]的度量,依赖于攻击者的攻击模型.需要考虑特定的攻击者,即拥有更多资源或先验知识的强大的攻击者,也许能够更成功地对匿名系统去匿名化.因此,能够应对更强大的攻击模型的匿名系统,可以提供更强的匿名保障.
在经典的Dolev-Yao 模型中,攻击者可以窃听、阻止和截获所有经过网络的消息;可以存储所获得或自身创造的消息;可以根据存储的消息伪造并发送该消息;可以作为合法的主体参与协议的运行.在匿名通信环境下,攻击者感兴趣的是哪些通信正在发生、谁在发送消息、谁在接收消息、通信模式怎样,甚至破坏和操纵通信.表5 从能力、视野、灵活性、参与性、先验知识和资源这6 个方面给出了不同的攻击者属性,一个攻击者可能同时具有多个属性.攻击者的目标、特征和知识是什么,这些都是度量可能需要考虑的因素.
根据不同的应用场景,成功有不同的定义方式.在匿名通信系统中,当攻击者能够识别消息的发送方或接收方时,当攻击者从可能的通信目标中识别出若干个时,当攻击者能够使用节点、带宽等给定数量的资源攻陷通信路径时[35],都可以称为成功.例如,在Tor 中,当攻击者控制用户洋葱路由路径上的所有中继时,若发生路径变节,则攻击成功.
文献[36]在一部分节点被攻陷的情况下,用条件概率、全概率公式讨论在不同路径选择策略(固定长度路径和可变长度路由)和不同路径拓扑(简单路径无环路和复杂路径有环路)的情况下,当敌人掌握一定信息量,利用攻击者算法和消除规则,对发送方成功被识别的概率进行分析,如图14 所示.得出的与直觉不同的结论是:随着路径长度的增大,发送方被发现的概率并不总是下降.这是因为,当路径长度增大时,路径中选择到恶意节点的可能性也可能增加,攻击者将获得更多、更好的路径相关信息,从而提高了识别的概率.

Table 5 Attacker propertities表5 攻击者属性

Fig.14 Adversary algorithm to identify sender图14 攻击者识别消息发送方算法
使用对手的成功概率来量化隐私的指标,表明了对手在任何一次尝试中成功的可能性,或者他们在大量尝试后成功的频率.攻击者成功概率的度量可以表示为公式(16):

当攻击者做出有效识别的概率高于阈值τ时,攻击成功.低成功率表示高匿名度.
专注于匿名通信技术的研究倾向于使用熵、不可区分性等指标,关注匿名技术的有效性.专注于匿名系统攻击的研究工作倾向于使用基于时间、成功概率的指标,关注于敌手能否攻击成功.正如我们之前在第2.7 节讨论熵方法时提到的:当从更多角度去评估匿名系统时,会有更全面的结果.“攻击”和“防御”视角都是合理的选择,匿名系统抵制攻击的能力也能反映出匿名程度的强弱.
4.2 基于博弈论的匿名依赖关系度量
博弈论方法适用于一个用户的行为影响其他用户匿名的场景,为了考虑这种相互之间匿名性的依赖关系,从博弈论角度度量一个用户的行为对另一个用户的匿名性所造成的后果是值得探讨的方法.文献[25]从博弈论角度研究匿名网络设计者与攻击者之间的相互作用,讨论匿名性最大化问题,将优化匿名性问题描述为匿名系统设计者与攻击者之间的零和博弈.攻击者的目标是选择系统中节点的一组子集进行监控,使得路由的匿名性最小化,匿名通信系统设计者的任务是通过选择系统中节点的一组子集,生成独立传输路由,以规避流量检测,使得路由的匿名性最大化.
4.3 基于时间的匿名度失效情况度量
基于时间的度量侧重于将时间作为攻击者为了攻陷用户的隐私需要花费的资源,随着时间的推移,匿名通信系统提供的匿名性可能会降低[37].度量攻击者成功之前的时间,是假设系统匿名性最终会失效,计算攻击者被混淆无法正确追踪之前的时间[38],是假设系统匿名性最终将得到保证.
最普遍的是度量攻击者成功之前的时间.文献[37]假设:对于拥有一组勾结节点的攻击者,当一个特定的发起者持续地与一个特定的响应者通过路径重组进行通信,并且攻击者可以在传输的数据包中获得能够唯一标识重复连接的会话标识信息时,则匿名通信协议会受到攻击从而降低匿名性.该文给出了Crowd、Onion Router、Mix-net、DC-net 这4 种匿名协议在面对所描述的攻击时能够保持匿名的时间上限,结果显示:随着时间的推移,足够多的攻击者能够收集到足够多的信息,因此攻击者识别特定会话发起者的概率增加,从而破坏发送方匿名.
攻击者的目标通常不仅仅是在某一时刻破坏隐私,而且是随着时间的推移,跟踪攻击目标的位置.文献[39]用最大跟踪时间来衡量攻击者的跟踪能力,最大跟踪时间定义为攻击目标u的匿名集大小保持为1 的累计时间,见公式(17):

这个指标假定攻击者必须完全确定,即匿名集的大小必须为1,才能成功.现实中,如果攻击目标的匿名集中只有少量用户,攻击者也可能有能力继续追踪.
文献[24]提出延迟攻击,攻击者可以利用Tor 中通过连接延迟泄露的信息,在多次重复连接后,推断出客户端的位置.最近的研究提出了Tempes 度量方法[40],证明随着时间的推移,系统匿名性有可能显著退化;并展示了客户端移动性、使用模式和网络拓扑结构随时间的变化对Tor 匿名性的影响.延迟攻击与Tempest 攻击如果同时使用,将会增强攻击者去匿名化匿名系统用户的能力.
4.4 观测值与真实结果间的误差度量
基于误差的度量方法,输出攻击者在估计时所犯的错误的量化值.在统计参数估计中,使均方误差最小化是共同的目标,作为匿名性的度量,均方误差描述了攻击者的观测值y与真实结果x之间的误差,表示为公式(18):

文献[26]提出了一种基于最小二乘法的分析方法,该方法允许描述对手在用户行为、匿名提供者行为和虚拟策略方面的分析误差.针对特定mix 网络的特定情况,论述了如何在给定如匿名性等隐私目标的情况下,使用性能分析来设计最优的策略以保护该目标.文献[41]提出了网站指纹攻击防御的安全界限,利用实践中估计的误差来评估所获得的隐私保障.
4.5 基于差分隐私的不可区分性度量
源于数据隐私领域的差分隐私[42]保护技术,在匿名通信领域也可以找到应用.基于差分隐私表示匿名程度的方法输出评估目标的不可区分性,例如攻击者是否能够区分消息的发送者或接收者,表示为公式(19):
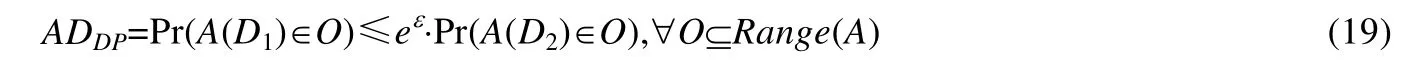
如果一种随机化算法A作用于两个相邻数据集D1和D2得到的结果O小于ε,则称该随机化算法满足ε-差分隐私.Pr 表示隐私信息泄露的风险;不同的ε值表示不同的隐私保护强度,ε越小,隐私信息泄露的风险越低,隐私保护强度越高,匿名程度越高.
文献[27]提出了基于差分隐私的严格形式化方法来量化Tor 面对结构攻击时所能提供的匿名性,例如攻击者能够破坏Tor 节点,从而执行窃听攻击,以消除Tor 用户的匿名性,为Tor 以及其他路径选择算法(例如DistribuTor、SelekTOR 和LASTor)建立了针对各种结构攻击最坏情况时的匿名边界,产生了第1 个严格的针对不同路径选择算法的匿名比较.其他,例如流量分析抵制系统Vuvuzela[43]和Stadium[44]、以保护用户隐私为目标的Tor 网络测量系统PrivCount[45],都采用了差分隐私的思想来精确证明系统的隐私保障.
4.6 基于数据隐私方法的匿名度量
匿名度量属于隐私度量中针对匿名性问题的研究,一些隐私度量方法尽管起源于其他领域,也在匿名性度量中得到了应用,例如数据隐私[46,47]度量.以数据库隐私领域为例,k匿名的概念与匿名通信领域中匿名集的语义相似,k匿名模型是数据隐私领域大多数匿名模型的基础,通过保证数据表中任何一条记录的准标识符都和至少k-1 条记录相同,切断准标识符值和敏感属性值的一一对应关系[48].文献[49]引入了发送方k匿名和接收方k匿名的概念,发送方k匿名保证攻击者试图确定消息的发送方时,只能将搜索范围缩小到有k个用户的组中;接收方k匿名与此类似,将可能的接收方缩小到大小为k的组中.k匿名的方法可以表示为公式(20):

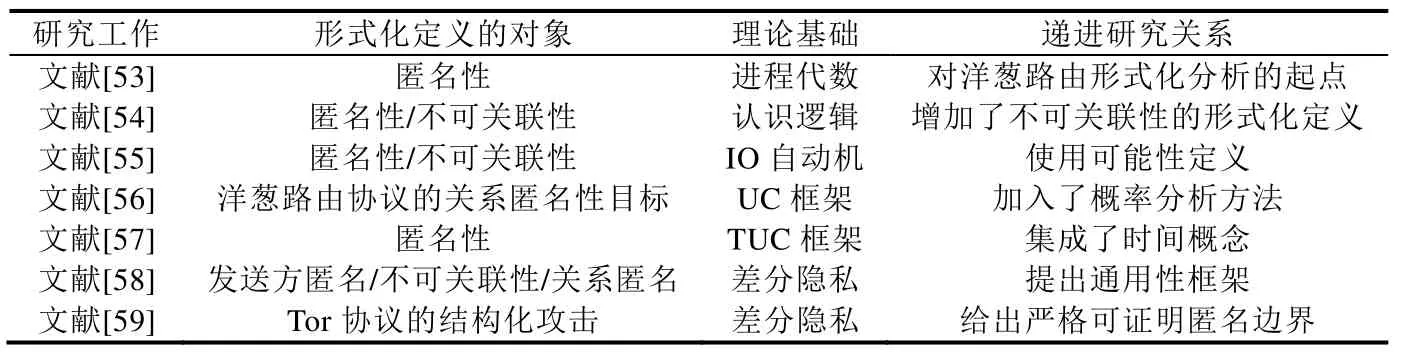
当数据表中记录的条目数或者通信系统中匿名集的大小满足≥k的最小要求时,则保持匿名性,低于最小值( 文献[50]基于贝叶斯推理进行匿名原始数据的推断,通过比较构建原始数据二叉树图和推断数据二叉树图之间的差异,来衡量信息泄露的风险.源于网络通信领域的隐私度量方法也在其他隐私保护领域得到了应用,例如,文献[51]以云数据为研究对象,讨论了信息熵、集对理论、差分隐私等隐私保护度量方法. 形式化方法已经以不同程度和不同方式应用于计算系统生命周期的各个阶段[52],使用形式化方法验证身份认证相关的安全协议已成为标准实践.随着隐私保护得到越来越多的关注,隐私安全目标的形式化方法也变得不可或缺.我们选出7 篇高质量文献[53-59],展示了针对或应用于洋葱路由协议的形式化方法,并在表6 中突出体现了不同文献在形式化的对象、具体方法等方面的区别.选择这几篇文献是因为洋葱路由协议作为成功的匿名通信协议,以Tor 系统的形式,被数以百万的用户用来保护他们的安全和隐私.与实用的设计相比,这一领域的理论研究相对年轻,针对其隐私属性形式化分析方面的研究较为有限,相信未来会有更多的研究工作. Table 6 Comparsion of the formal methods for anonymity表6 匿名形式化方法比较 文献[53]采用进程代数的方法,提出匿名性的形式化定义,通过分析洋葱路由协议进行验证,得出定性的结论,未进行定量的研究.文献[54]从认知逻辑的角度,除了给出匿名性的定义外,还对不可关联性进行了形式化定义,通过分析洋葱路由和Crowd 协议进行了验证.文献[55]给出了洋葱路由协议的IO 自动机模型,描述在可能定义下保证匿名性和不可链接性的情况.文献[56]使用UC(universally composable)框架,提出了匿名通信黑盒模型,加入概率分析方法,抽象出洋葱路由的基本属性,量化敌手利用用户的概率行为的知识来识别用户所能获得的收益.文献[57]针对其他框架都不能对流量相关时序攻击进行建模,提出了时间敏感的UC 框架TUC.该框架在异步通信模型中集成了时间概念,针对存在能够发起与流量相关的定时攻击的时间敏感攻击者的场景,对所提供的匿名性进行严格的证明,并面向Tor 提出了一种新的网络指纹攻击防御策略.文献[58]提出一个与UC 框架兼容的通用框架AnoA,用于定义、分析和量化匿名协议的匿名性,结合框架提出了基于差分隐私的发送方匿名、发送方不可关联、接收方匿名和关系匿名等匿名概念;通过对Tor 网络的实例分析,验证了当前Tor 的固有缺陷;针被动攻击模型,以定量的方法给出了匿名保证.文献[59]在基于AnoA 通用框架的基础上加以扩展,提出一个使用严格证明边界来评估Tor 的匿名性的框架MATor,评估考虑到Tor 的实际路径选择算法、Tor 共识数据、用户的偏好以及网络状态的影响,从而解决了实际部署Tor 的实时现实特征对用户匿名性的影响. 匿名度量与匿名系统本身机制和攻击模型有很大的关系,匿名机制自身的结构可能导致攻击模型出现差异,而攻击者采用的攻击方式也可以导致匿名度量方式出现差异,因此,本节在分析匿名攻击方式的基础上分析和比较不同的匿名度量方法.由于Tor 是匿名通信网络中实际上应用得最广泛的研究平台,本节主要以基于Onion Router/Tor 匿名系统面临的去匿名化攻击为背景,综合文献[1,2,4,24,60-62]介绍了匿名攻击技术,并给出可用的分类,见表7. Table 7 Attack and defense on anonymous communication表7 匿名通信系统的攻击和防御 表8 按照本文的阶段划分小结面向匿名通信系统的典型匿名度量的方法、主要特点和文献信息.我们对攻击技术和度量方法所做归类的边界并不是严格的,归类并不意味着它不能用于其他领域,不同归类中的攻击方法和匿名度量方法可能会有交叉.以度量方法为例:相同的度量方法可能出现在不同的研究领域中,不同输出的匿名度量结果也可能使用同样的基本理论.例如,PrivCount[45]使用了差分隐私的度量方法,但它也是针对Tor 实际部署系统的度量.我们的归类思路主要考虑从匿名技术设计的角度出发,基于该方法首次提出时面向的背景进行归类整理. 表格中度量的通用性高中低的标注,根据该度量方法是否可以跨多个领域使用进行判断.标注为High 的度量方法理论上可以在不同的研究隐私保护领域使用;标注为Medium 的度量方法在实用性和理论性之间获取平衡;标注为Low 的度量方法尽管实用和有效,但仅依赖于特定匿名协议.表格中对每种度量方法标注的应用是根据提出该方法的文献中面向的匿名系统或协议,该方法在其他研究中也可能有不同的应用. Table 8 Anonymity metrics summary表8 匿名度量方法 Table 8 Anonymity metrics summary (Continued)表8 匿名度量方法(续) 新的匿名通信系统的设计迅速发展,例如:抵制流量分析的Aqua[71]、Herd[72]、Loopix[65]系统;基于概率转发路由的AnonPubSub[73]系统;针对审查抵制的Front-domain[74]、Marionette[75]、自由瀑布[76]系统;基于重加密的 cMix[77]系统;基于 Ad-hoc 和无线传感网的匿名协议[78,79];将匿名作为网络层基础设施提供服务的HORNET[80]、TARANET[81]系统;面向未来软件定义网络(software defined networks,简称SDN)架构的匿名系统iTAP[82]、Mimic[83]系统;以及面向点对点短信应用的Vuvuzela[51]系统和匿名文件分享Riffle[84]系统等.随着新的网络匿名通信系统出现,能够评估和比较系统向用户提供的隐私变得越来越重要,匿名性的度量面临新的挑战. 6.1.1 基于熵度量应用于新兴匿名系统 基于信息论的度量方法对匿名度量有重要的研究意义,并得到了广泛的应用.随着匿名系统的迅速发展,基于熵的方法也被用于度量新兴匿名网络的隐私安全目标,除了发送方匿名的安全目标外,也被用于测量匿名网络中其他方面的不确定性,例如,路径选择的随机性等,在未来的匿名度量研究中具有广泛的应用前景. 文献[64]面向延迟容忍网络(delay tolerant network,简称DTN)场景,在分组洋葱路由的基础上提出多复本转发方法.应用基本香农熵的方法,讨论该文所提方案的安全性.由于分组洋葱路由的特点,区别于原洋葱路由方案,该文对分组洋葱结构下路由选择、发送方以及接收方被攻击者推测出的概率进行计算,利用基本的信息熵,衡量了系统的路径匿名度、发送方匿名度和接收方匿名度. 图15 描述了分组洋葱路由结构,发送方vs、接收方vd、洋葱节点被分为{R1,R2,…,Rk}组,图中k=3,每个分组中有g个洋葱路由节点,ri,j是洋葱组Ri中的第j个节点,转发消息时,vs可以将消息发送到R1组中的任何节点r1,j,Ri-1组中的节点可以将消息转发到Ri中的任何节点,最后一组的节点把消息转发给vd. Fig.15 Group onion routing for delay tolerant networks图15 面向延迟容忍网络的分组洋葱路由 针对DTN 的不稳定连接特性,多复本转发方案可以保证消息的可到达率.将每一条消息复制为L个复本,从发送方离开,送给第1 组中的L个节点;然后,这L个节点发送给下一组中的L个节点.以此类推,直到接收方收到消息.在这种分组转发协议下,分析得出基于熵的路径匿名度的计算方法,见公式(21): 其中,n表示网络中节点的数量,η表示两个节点之间的跳数,g是每个洋葱组中节点的数量,co是路径上被攻击者攻陷的节点数量. 文献[65]提出的Loopix 低延迟匿名通信系统由客户端、提供方和分层mix 节点构成,如图16 所示.利用覆盖流量和消息延迟,提供双向的第三方发送方匿名、接收方匿名和不可观察性匿名,通过生成客户端覆盖循环、客户端覆盖丢弃、mix 节点覆盖循环这3 种覆盖流量来抵制攻击者的流量分析,并利用信息熵分析与计算系统中消息的熵在不同延时参数和不同流量率参数下的变化. Fig.16 Low latency anonymous communication system Loopix图16 低延迟匿名通信系统Loopix Loopix 系统中,mix 节点接收和输出的信息流建模为泊松过程,mix 中消息的平均数量满足λ/μ泊松分布.攻击者对mix 节点的输入和输出消息进行观察,推断mix 池中有k条消息,在任何消息离开之间,能观察到又有l条消息到达mix,继续推断mix 池中混合了k+l条消息.然后,攻击者尝试通过对一条输出消息m的观察,来关联mix 节点池中的k+l条消息,增量计算每条输出消息的熵.用mix 节点输出的消息与过去输入消息之间关联分布的熵Ht作为系统的匿名度量,通过l的大小、前一时刻消息的熵Ht-1以及自上次发送消息以来接收到的消息k的数量计算Ht的值,如公式(22): 区块链作为解决数据隐私安全问题的重要手段,被越来越多的应用所使用[66].针对区块链应用中的隐私保护问题,研究当前主流加密代币使用的隐私保护策略,包括对发送方、接收方和内容进行匿名处理等环节.加密货币的每个用户的行为都会影响其他用户的匿名性,匿名程度是评估区块链隐私安全目标的有效指标,信息熵评估应用于区块链系统具有一定的应用前景. 6.1.2 Tor 实践中的度量 Tor 项目组在匿名领域开展着前沿的研究工作,Tor 也是目前最流行和最大的已部署匿名网络,由数千个志愿者运行的中继和数百万用户组成.Tor Metrics 官网[85]可以查看到从公共Tor 网络和Tor 项目基础设施收集的统计数据,截止到2020 年11 月,Tor 隐藏服务站点超过20 万,中继节点超过7 千个,连接用户数约400 万.如果想更好地理解Tor 网络对观察或操作部分网络的攻击者提供了多少匿名性,需要数据来监视、理解和改进网络,需要数据来检测可能的审查事件或对网络的攻击.但是,隐私保护是Tor 网络的目标,因此不容易与广泛的数据收集相结合,在保护隐私的前提下,进行数据采集和匿名度量.针对实际部署匿名系统Tor 和针对Tor 的改进工作,也提出了不少新颖而有针对性的度量方法[67-69,86,87]. 文献[35]对Tor 的路径选择算法进行了分析,包括当前使用的路径选择算法和提出的改进方案.分析的目的是找出在选择Tor 节点构建匿名电路的方案中,哪一种更安全.该文基于从部署的Tor 网络收集的数据模型,讨论不同路由算法下的攻陷率,以反映系统的匿名性和性能.在恶意节点拥有100MB/s 带宽资源预算的前提下,结果表明:尽管均匀路由选择方案具有较高的熵值,但是当攻击者拥有大量低带宽恶意节点时,会导致80%的匿名路径被破坏.带宽加权路由选择方案则具有较好的安全性,因为无论攻击者如何分配资源,造成的破坏都不会超过匿名路径的20%. Tor 的隐私目标,会使得常用的度量方法无效或产生隐私泄漏风险.文献[45]提出PrivCount——一种以用户隐私为主要目标的Tor 网络测量系统,可以安全地聚合跨Tor 中继节点的测量值,并随着时间的推移产生不同的隐私输出.为了提供Tor 用户和流量的准确模型,PrivCount 对Tor 进行了有充分广度和深度的测量.结果表明:针对给定时间内71 万用户连接,只有55 万的活跃用户,Web 流量占据Tor 的数据字节的91%;而且中继节点连接策略的严格程度,显著影响着它们所转发的应用程序数据的类型. Tor Metrics 网站[76]可查询到关于用户、中继节点、流量等可视化数据,可直观了解Tor 网络的情况,具体见表9. Table 9 View visualizations of statistics collected from the public Tor network and from Tor project infrastructure表9 Tor Metrics 提供可视化统计数据,数据从公共Tor 网络和Tor 项目基础设施收集 图17 显示了数据是如何通过Tor Metrics 提供的服务,收集、归档、分析和呈现给用户的. Fig.17 How data is collected,archived,analyzed,and presented to users by Tor Metrics图17 Tor Metric 对数据收集、归档、分析和呈现给用户的过程 Tor 的中继和桥收集关于其使用情况的汇总统计信息,例如每个国家的带宽和连接的客户端.源聚合用于保护Tor 用户的隐私,因此IP 地址被丢弃,只报告从本地数据库映射到国家IP 地址范围的国家信息,这些统计数据定期发送给目录管理机构.Concensus health 包含当前共识文件的统计信息和投票,以方便调试目录共识过程.CollecTor 从目录权威机构下载最新的服务器描述符、包含聚合统计信息的额外信息描述符和共识意见文档,并将它们归档.这个归档文件是公共的,大多数服务使用metrics-lib 解析描述符,可以使用metrics-lib Java 库解析归档文件的内容来执行数据分析.为了提供对存档的历史数据的可视化访问,Tor Metrics 网站包含许多可定制的图表,用于显示用户、流量、中继、桥和应用程序下载等统计数据,这些统计数据在请求的时间段内,经过过滤,到达特定的国家.ExoneraTor 维护一个Tor 网络内IP 地址的数据库,回答在给定的IP 地址上是否有Tor 中继在给定的日期运行的问题,ExoneraTor 可以为每个中继存储多个IP 地址,并且能够存储中继是否允许将Tor流量传输到开放的Internet 的属性.为了提供对公共Tor 网络当前信息的方便访问,Onionoo 通过HTTP 提供JSON 文档,对于需要显示中继信息、历史带宽、正常运行时间和共识权重信息的应用程序可以使用该协议.中继搜索就是这样一个应用程序的例子,中继操作人员、监视网络健康状况的人员和使用Tor 网络的软件开发人员都可以使用中继搜索.另一个应用程序的例子是metrics-bot,它定期地向Twitter 等社交网络发布快照,包括国家统计数据和绘制已知中继的世界地图. 6.2.1 匿名度量组合方法 近年来,匿名通信系统出现了一些新的技术,例如,规避审查的隐蔽接入技术[73]、利用SDN 构建匿名隧道[82]、组合ISP 服务构建匿名域[88]等.一个单独的度量标准不可能涵盖隐私的整个概念,因此,更完整的隐私评估可以考虑通过使用来自不同输出类别的度量组合获得.针对新兴的匿名技术和未来的网络环境,对匿名度量方法进行扩展和组合[89],以适应新的匿名通信系统,也是具有一定应用前景的研究方向. 对于采用组合方法提供匿名性保证的系统,度量方法也应该考虑组合的可能.归一化是一种组合方法,例如归一化熵、归一化条件熵等,是用一种指标对另一种指标进行标准化.几种指标的线性加权,按照各目标的重要性赋予相应的权系数,对其线性组合进行多目标优化求解,寻找度量的评价函数,也是一种组合方法.多个不同实体的相同度量值如何组合、同一个实体的不同度量值如何组合、经过组合的度量方法是否扩大了应用的范围、是否能够应用于新的系统,都是值得研究的问题.文献[70]使用标准熵、猜测熵以及经验度量这3 个匿名指标综合评估系统的匿名性.经过组合的度量方法,如果能够保留这些度量方法的优点,同时减少它们的缺点,就能形成新的有效的度量,从而应用于新的匿名系统. 6.2.2 通用度量模型和评估系统 在匿名的形式化研究工作中,提出了一些通用的匿名框架.文献[63]比较了不同匿名框架,例如AnoA 框架、Hevia 框架、Bohli 框架、Gelernter 等的概念定义,提出了一个完整的层次结构,对概念进行了统一的定义和一致性研究.因为不同研究之间命名方式的差异、匿名性概念强弱的差异等,阻碍了对不同匿名目标的理解和比较,阻碍了匿名通信系统的比较和改进,这方面的工作也是本领域未来需要研究的方向. 匿名度量的目标是对匿名系统所能提供的匿名程度进行量化,度量的结果表明:系统在面对各种攻击场景时,能为用户提供多少匿名性,有助于匿名系统的对比,也可以为不同匿名需求下设计和改进匿名系统提供建议.量化方法的选择与攻击者的不同攻击方法、与匿名系统各自不同的属性特点有直接的关系.有的度量方法较为直观,有些度量方法在概念上就较为困难.正是由于度量方法如此多样和复杂,对它们的正确选择和应用就极具挑战性.匿名系统研究者难以找到合适的方法评估自己的创新研究,而系统评估研究者并不清楚匿名系统研究者面临的困难.为了促进研究者选用合适的方法进行匿名系统的比较和改进,同时把这个问题暴露在从事信息系统评估的研究者面前,建立一个匿名系统的研究者和系统评估的研究者之间彼此了解的桥梁,逐步克服当前不同的匿名度量机制之间进行定量比较的困难等目标,本文对通信系统中匿名性度量的研究历程和发展现状进行了综述.针对匿名通信系统,力图梳理和构建出一个较为清晰的度量研究的概貌,并强调了度量在研究上的重要性,给进一步的研究提供一点参考.匿名度量研究开始的初期阶段,形成了匿名性定义的共识,使用基于匿名集大小和基于概率分析的方法来度量匿名性.接着,信息论在匿名度量领域得到了广泛应用,我们针对不同场景对基于信息论的熵度量方法进行了具体的分析和比较.随着匿名度量研究的进一步发展,表达匿名程度的度量指标也越来越多样,关联性、时间和不可区分性等多种指标被提了出来,作为度量的输出来衡量系统的匿名程度.从综述可以看出,并没有一种既实用又准确的匿名度量方法能够满足所有匿名通信系统的需要.近年来,网络匿名通信系统得到了迅速的发展,匿名度量有助于增强数字世界中用户的隐私保护.信息熵等已有的成熟度量方法在新兴匿名系统中的应用,现实中已经广泛部署的匿名通信系统的匿名性度量,以及通过对度量方法的扩展或组合形成新的度量方法以适应特定新场景的匿名需求,都是有应用前景的研究方向.由于匿名目标的具体定义往往针对特定的用例而特别加以创建,命名和形式化通常是不兼容、不一致的,使得不同匿名度量机制之间的定量比较具有一定的难度,也阻碍了匿名系统的比较和改进.因此,对匿名系统、攻击模型和度量方法这3 个方面进行统一的模型抽象,未来值得进一步研究与探索.4.7 基于形式化的可证明性度量
5 分析与比较



6 挑战和发展
6.1 基于具体系统的具体挑战



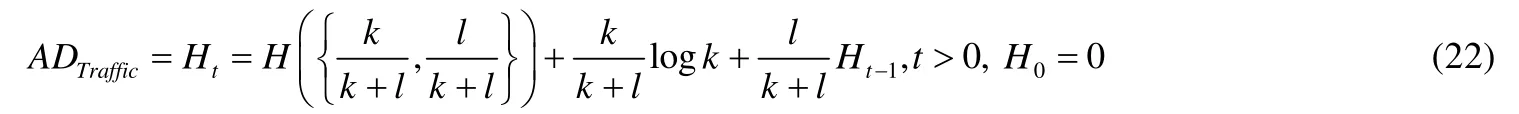


6.2 发 展
7 结论

