超孔隙水压力对盾构隧道极限支护力影响研究

陈相宇, 潘 茜, 丁建军

(佛山轨道交通设计研究院有限公司, 广东 佛山 528000)

0 引言

城市过江隧道修建过程中，不可避免需要穿越江河两岸浅覆土的漫滩区段，而漫滩段往往分布着较厚的富水砂层。富水砂层工程特性复杂，盾构在该类地层中施工时，易发生开挖面土体失稳，甚至地表塌陷情况[1]。富水砂层中盾构施工对孔隙水压力产生扰动，改变了影响区内土体的应力应变状态及渗流状态，进而对盾构隧道开挖面稳定性产生影响[2]。研究盾构施工引起地层孔隙水压力反应的方法主要包括现场监测、理论计算、有限元模拟等。

在现场测试数据的总结分析方面，Broere[3]对Heinenoord隧道盾构掘进过程引起的地层孔隙水压力变化进行监测，分析总结了孔隙水压力随盾构掘进开挖的变化规律；易宏伟等[4]对软土地层中盾构施工期间孔隙水压力反应规律进行了研究总结。

基于Mohr-Coulomb屈服准则，肖立等[5]推导了考虑土体内摩擦角φ时盾构掘进引起的超孔隙水压力计算公式；魏新江等[6]通过应力释放理论，推导了隧道衬砌周围土体的初始超孔隙水压力计算公式；王志良等[7]基于Mindlin解和Henkel公式推导了盾构掘进开挖面前方超孔隙水压力的分布特征；丁智等[8]采用数值积分的方法推导了软土区盾构掘进引起的超孔隙水压力计算公式。

随着计算机技术的进步，有限元法也广泛应用于孔隙水压力的分析与研究。文献[9-11]通过数值分析，对渗流场应力场耦合效应及开挖面稳定性进行了研究。国内外相关学者探索研究了极限平衡法在砂性土开挖面极限支护压力计算方面的应用，总结了修正楔形体模型极限支护压力公式[12-14]。

目前研究成果多侧重于对孔隙水压力变化规律的总结以及超孔隙水压力的计算方法研究，或在未考虑超孔隙水压力的影响下，对盾构开挖面极限支护力进行计算分析，尤其在富水砂层孔隙水压力反应研究中，考虑超孔隙水压力对开挖面极限支护力影响的研究成果较少。本文基于某越江公路隧道工程，对盾构掘进前方地层进行孔隙水压力现场测试，通过实测数据，分析总结盾构施工期间地层孔隙水压力的空间分布特征以及盾构施工引起的孔隙水压力变化规律。基于变分学方法，将极限支护力的求解转化为考虑多维约束的函数极值问题，进而研究超孔隙水压力对盾构隧道极限支护力的影响，提出修正的极限支护力计算公式，并对盾构泥水舱压力的设置提出建议，以指导实际施工。

1 工程概况

本文依托的工程，包括2条并行的越江隧道，单条隧道长度约1.6 km，采用泥水平衡式盾构，盾构开挖直径11.65 m。盾构从东岸始发井开始掘进，穿越江底后到达西岸接收井。盾构隧道在江底段主要穿越强风化砾岩、中风化砾岩层；靠近盾构接收井的河西岸漫滩段，隧道上半断面及上覆地层分布着较厚的富水粉细砂层，局部存在卵石、圆砾。本文研究对象为河西漫滩段的粉细砂层，本工程地质勘察资料揭示，该处粉细砂层呈褐黄色，湿-饱和，稍密-中密状，透水性强，如图1所示。

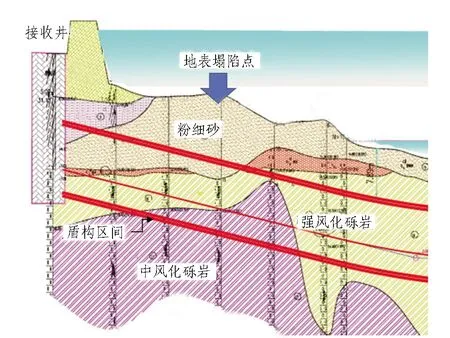
图1 隧道地质纵剖面

先行线隧道掘进至河漫滩地层时，盾构开挖面前方约1倍洞径范围地表出现较大的沉降，局部区域出现地表塌陷，见图2。

图2 河漫滩地表塌陷

2 孔隙水压力测试数据分析

为探明盾构掘进前方富水砂层孔隙水压力波动及分布情况，在后行线掘进至河漫滩地层时，进行了孔隙水压力现场测试试验。

2.1 孔隙水压力测试方案

在孔隙水压力测试区段，盾构主要穿越粉细砂层，隧道埋深较浅，覆土厚度约为0.6倍开挖直径。测试方案中，沿隧道纵向等间距布置5个垂直于隧道轴线的孔隙水压力测试断面，编号为Section 1—Section 5，相邻测试断面间距d=D/2。每个测试断面在隧道顶部土体中M1、M2点埋设2个孔隙水压力计，与隧道拱顶竖向距离分别为1.0、3.0 m。重点测试断面Section 3，在隧道横向水平轴线设5个孔隙水压力测点N1～N5，相邻测点间距d=D/2，如图3所示。

图3 孔隙水压力测试方案示意图(单位: m)

2.2 隧道纵向孔隙水压力分布

选取Section 2、Section 3断面的测试数据，分析盾构靠近、通过以及离开测试区的整个施工过程中地层孔隙水压力的分布及变化规律，变化曲线分别如图4和图5所示。

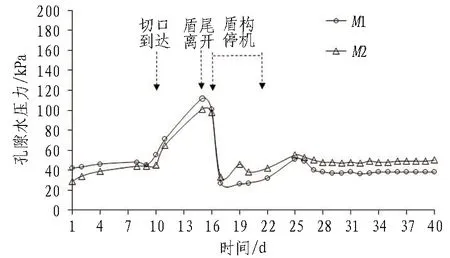
图4 Section 2孔隙水压力变化曲线

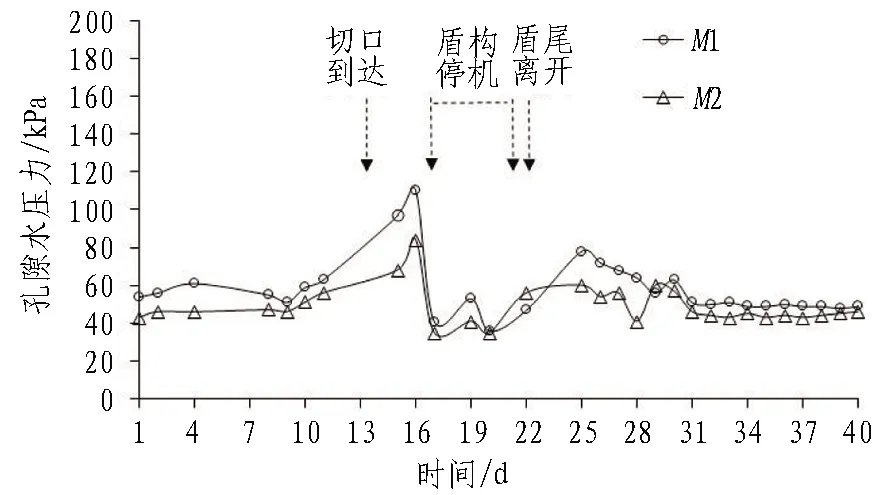
图5 Section 3孔隙水压力变化曲线

随着盾构施工时间的推移及盾构与测试断面空间关系的变化，盾构施工对地层孔隙水压力的影响可分为盾构靠近、穿越以及离开测试断面3个阶段。这3个阶段包括了盾构与测试断面的空间关系变化全过程。

测试方案中，Section 3作为重点测试断面，沿隧道横向埋设了孔隙水压力计，故下文以该断面的孔隙水压力测试数据为例重点分析。

1)盾构靠近阶段。盾构朝着测试断面Section 3的方向掘进，并逐步靠近孔隙水压力测点。该阶段刀盘在盾构推力作用下，挤压前方及两侧一定范围内的土体，致使挤压影响区域孔隙水压力增加。

2)盾构穿越阶段。盾构到达并穿越重点测试断面Section 3的过程中，测点孔隙水压力快速上升，并达到整个过程的孔压峰值。现场测试数据显示，该阶段M1测点0.110 MPa、M2测点0.084 MPa，可见孔隙水压力的峰值基本为该阶段初始状态下(盾构刚到达重点测试断面)的2倍。在测试期第16—22 d(此时盾构刀盘位于Section 4—Section 5)，盾构停机1周，在刚发生停机时，孔隙水压力迅速消散，下降60%后测值为0.041 MPa。随后施工单位进行了壁后注浆，壁后注浆期间，测试断面Section 3的孔隙水压力值受注浆压力影响在波动中呈抬升状态。

3)盾构离开阶段。盾构恢复施工并正常掘进至盾尾离开测试断面Section 3，测点M1的孔隙水压力也随即上升，并达到该阶段的最大值，测值为0.078 MPa。盾构持续掘进，测点孔隙水压力逐渐降低。随着时间的推移，盾构通过后7～8 d，测点孔隙水压力趋于稳定并维持在盾构到达测试断面Section 3之前的水平。

通过测试断面Section 1—Section 5 的超孔隙水压力计算可知，盾构到达第1个测试断面Section 1时，该断面测点处超孔隙水压力上升到35 kPa；Section 2、Section 3测点也产生了明显的超孔隙水压力；距离盾构开挖面较远的测试断面Section 5，测点处超孔隙水压力值小于5 kPa，认为不受明显影响。超孔隙水压力沿盾构掘进方向递减，如图6所示。

图6 隧道纵向超孔隙水压力分布曲线(M1位置处)

沿隧道纵向测点的数据表明，盾构靠近及通过测试断面期间，周围土体的孔隙水压力值明显上升并达到峰值；盾构通过测试断面后，孔隙水压逐渐消散，缓慢回落至初始水平；开挖面前方2倍开挖直径范围内为孔隙水压力扰动区，且随着与开挖面距离的减小，扰动程度增大。

2.3 隧道横向孔隙水压力分布

重点测试断面Section 3的横向单侧孔隙水压力测试曲线如图7所示。Section 3沿隧道横向共设5个测点，其中测点N3和N4因现场钻孔条件有限，未能达到设计孔深，测点位于隧道轴线水平面上方6.0、4.0 m。

(a)孔隙水压力变化曲线

根据沿隧道横向布置测点的数据可知，盾构穿越测试断面阶段，测点N1的孔隙水压力由0.074 MPa增大至0.080 MPa，产生的超孔隙水压力为6.0 kPa；测点N2孔隙水压力从0.088 MPa增大至0.092 MPa，在此过程中产生了4.0 kPa的超孔隙水压力；隧道横向1.5倍开挖直径距离的测点N4产生的超孔隙水压力较小，不到3.0 kPa；测点N5孔隙水压变化接近零值，认为几乎未受盾构施工影响。

盾构切口临近重点监测断面Section 3时，沿隧道横向测点数据及拟合结果表明：盾构施工时，将在开挖面两侧1.5倍开挖直径范围内地层中产生较明显的孔隙水压力扰动，且越靠近开挖面，扰动程度越大。

3 考虑超孔隙水压力变化的主动破坏极限支护力研究

3.1 主动破坏极限支护力pmin的确定

盾构施工中，如果设置的开挖面支护压力p小于开挖面发生主动破坏时所受的侧向土压力pmin，则可能会造成开挖面前方土体产生较大扰动，甚至存在塌陷的风险。基于极限平衡法的思想，确定主动破坏极限支护力pmin，并做以下假设。

1)研究对象为平面问题；

2)土体材料服从Mohr-Coulomb破坏准则；

3)开挖面前方地层发生失稳时，失稳土体为楔形体，其破坏面与开挖面上下顶点连接。

开挖面前方地层发生主动破坏时，失稳土体受力计算模型如图8所示。隧道底部距地表的垂直距离为h，隧道直径为D，通过开挖面的上顶点和下顶点的破裂面分别为l1,l2；σ1，σ2，τ1，τ2分别为作用在破裂面y1，y2上的法向应力和切向应力，kPa；p为盾构在开挖面上的作用力。

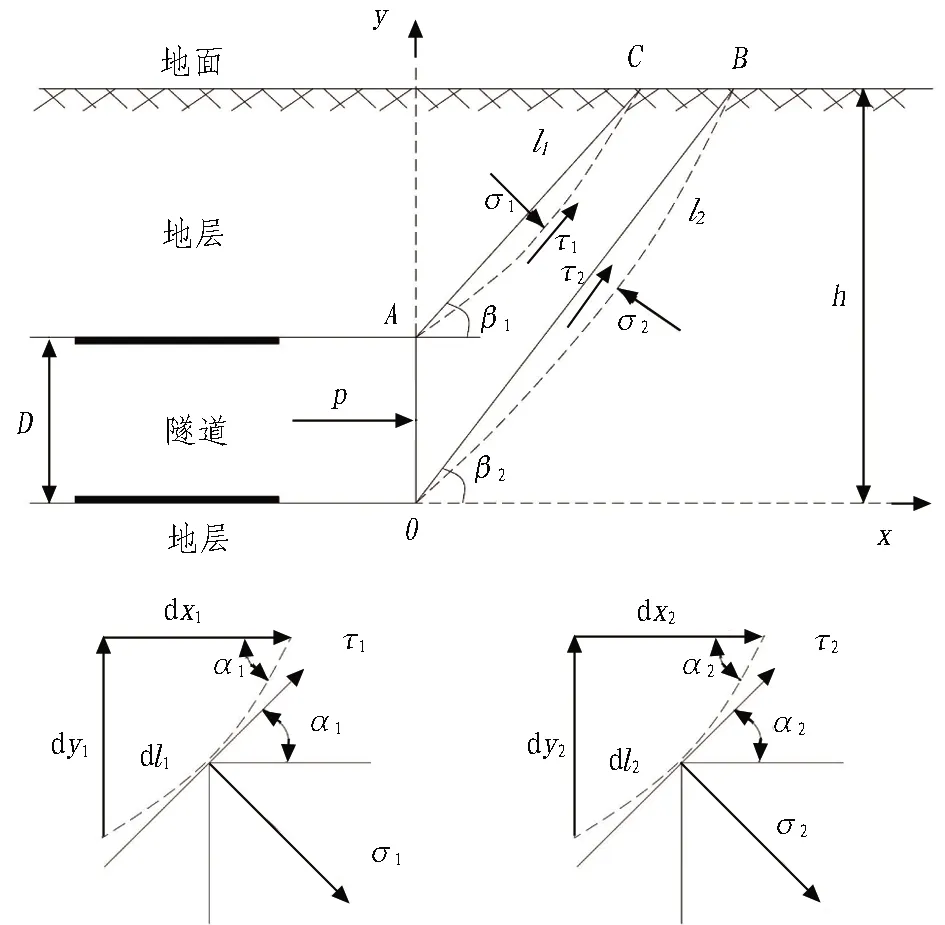
图8 开挖面前方破裂面受力分析图

单独考虑失稳土体AOBC的受力状态。

由∑x=0和∑y=0可以建立其处于平衡状态的力的平衡方程

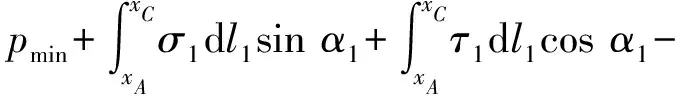
(1)

(2)

式(1)—(2)中：xA、xO、xB、xC为滑动块体顶点A、O、B、C的x向坐标；γs为土体重度，kN/m3；α1、α2、dl1、dl2、dx1、dx2的几何意义见图8。从图8还可得到：

dx1=dl1cosα1;dy1=dl1sinα1。

(3)

dx2=dl2cosα2;dy2=dl2sinα2。

(4)

破裂面上法向应力σ与切向应力τ服从Mohr-Coulomb破坏准则，则对应于破裂面l1,l2

τ1=σ1tanφ+c;τ2=σ2tanφ+c。

(5)

式中c为黏聚力。

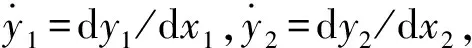
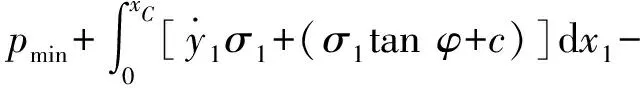
(6)

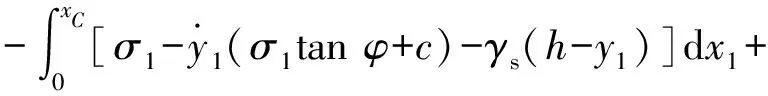
(7)

式(6)和式(7)分别为开挖面前方失稳时土体AOBC的2个受力极限平衡方程。

将破裂面可看作一个待求极值的泛函数，无法直接进行求解，需进行变分变换才能求解极值pmin。依据泛函数在约束条件下的变分法及相关边界条件，通过Lagrange乘子构造泛函数G，从而将上述的条件极值问题转化为无约束的极值问题。

(8)

g1=H1+λ1V1，g2=H2+λ2V2。

(9)

(10)

(11)

式(9)中λ1，λ2为Lagrange乘子。由变分学可知，破裂面方程y1(x)，y2(x)及破裂面上法向应力方程σ1(x)，σ2(x)需满足以下条件。

1)辅助函数H1，H2的Euler微分方程

(12)

(13)

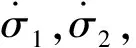
(14)

2)积分约束方程，即式(7)。

3)点B，C处的变分边界条件

(15)

式中δ为变分算子。

4)边界点的几何条件xA=xO=yO=0，yA=D，yC=yB=h。

根据上述边界几何条件，可知破裂面方程。破裂面y1(x)，y2(x)及破裂面上法向应力方程σ1(x)，σ2(x)的方程为

(16)

(17)

(18)

(19)

由式(10)和式(11)可知，破裂面方程y1(x)，y2(x)是线性方程，图8中的破裂面为直线。

破裂面设β1，β2为破裂面与x轴正方向的夹角。即破裂面方程y1(x)，y2(x)可写为

y1=x1tanβ1+D;

(20)

y2=x2tanβ2。

(21)

对比式(10)和式(11)，可得

λ1=-tan(φ+β1);

(22)

λ2=tan(φ-β2)。

(23)

将式(16)—(23)代入式(6)并化简，可得到主动破坏极限支护力pmin的目标函数f1。

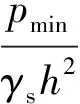
(24)

式中：pmin/γsh2为无量纲化值；f1是破裂角β1，β2的函数。

将式(16)—(23)代入式(7)并化简，可得到主动破坏极限支护力pmin的目标函数f2。

f2(β1,β2)=0。

(25)

式(24)和式(25)已将待求极值的泛函数转化为考虑多维约束的函数极值问题。然而，若直接求解式(24)和式(25)，可能带来计算量过大的问题。Matlab中的fmincon函数可用于计算多维约束非线性函数最大值的求解。利用该函数命令可先求出支护压力p的最小值(即求解-p的最大值)。其待求解的目标函数为式(24)，设定该函数约束条件如下：

1)β1，β2取值区间为[0,π/2]；

2)满足非线性公式(25)约束；

3)破裂面上切向应力τ大于0。

3.2 超孔隙水压力水对极限支护力的影响

富水砂层中开挖面前方土体受到盾构掘进的扰动，土体间产生超孔隙水压力Δμw(kPa)，土体强度随之降低[15]。

饱和土体任意截面总应力σ=σ′+μw。σ′为土体有效应力，μw为土体孔隙水压力。当孔隙水压力增加Δμw，则此时土体有效应力为(σ′-Δμw)。本文假设Δμw沿盾构隧道前方破裂面呈线性递减分布，且应力方向与土体有效应力相反，如图9所示。

图9 超孔隙水压力影响分布图

假定孔隙水压力在O点和A点处均为Δw，在B点和C点处均为0；则可知超孔隙水压力沿破裂面分布的计算式为：

(26)

(27)

式(18)和式(19)在考虑超孔隙水压力的影响后，可改写为

(28)

(29)

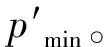
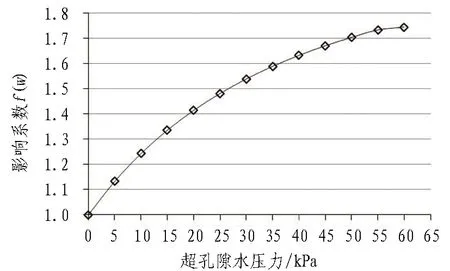
图10 影响系数随超孔隙水压力变化曲线

由图10可知，超孔隙水压力波动对开挖面前方极限支护力的设定影响较大。对应上文实测结果，当超孔隙水压力增加35 kPa时(如Section 1所示)，极限支护力的设定应比正常情况增加约59%；当超孔隙水压力增加13 kPa(如Section 2所示)时，极限支护力的设定应比正常情况增加约30%。

通过本工程盾构穿越的粉细砂地层取样及三轴压缩试验(固结不排水)，获得试样不排水抗剪强度ccu=9.6 kPa，φcu=30.1°。

图11示出当时塌陷区域盾构泥水舱压力曲线，因现场实际施工中未考虑孔隙水压力影响，该段掘进中泥水舱压力设置值偏低，仅为0.12～ 0.14 MPa，小于主动破坏极限支护力的理论计算值。隧道掘进至600环附近时地表出现较大的沉降，随着盾构持续低泥水压力掘进，至607环时出现了地表塌陷(见图2)。

图11 塌陷区域盾构泥水舱压力设置曲线

同时，通过黏聚力和内摩擦角对pmin的影响计算可知，黏聚力的存在及内摩擦角的增大，减少了实际需要的作用力大小，因而，在黏聚力和内摩擦角增大时，地层的自稳能力增加，更易保持开挖面的稳定，如图12所示。

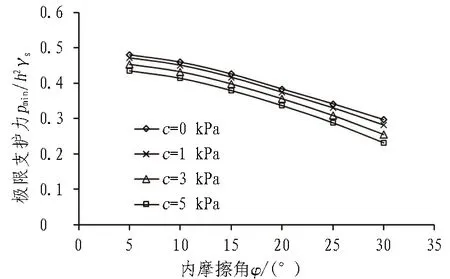
图12 黏聚力和内摩擦角对pmin 的影响曲线

4 结论与讨论

基于盾构施工期间孔隙水压力反应规律的分析以及超孔隙水压力对隧道开挖面主动破坏极限支护力影响的研究，得出以下结论：

1)富水粉细砂地层泥水盾构掘进施工时，将在开挖面前方及两侧的地层中产生孔隙水压力扰动区；该扰动区边界大致为开挖面前方2倍的开挖直径、开挖面两侧1.5倍开挖直径，且越靠近开挖面，扰动程度越大。

2)在考虑超孔隙水压力对极限支护力影响的工况下，基于极限平衡理论，提出修正的极限支护力计算公式；富水砂层中盾构施工应适当提升泥水舱压力，或采用全泥水平衡模式保持开挖面稳定，同时提高泥膜质量，保持匀速、较快的掘进速度，减小对孔隙水压力的扰动范围及扰动程度。

本文研究超孔隙水压力水对极限支护力的影响是基于二维的计算分析，未考虑三维作用，同时未计入孔隙水压力波动的时程影响，后续可结合理论计算、数值模拟对上述2方面开展研究。