面向运营隧道结构健康监测系统大数据压缩感知研究

吴贤国，邓婷婷，陈 彬，*，曾铁梅，陈虹宇，张凯南

(1.华中科技大学土木与水利工程学院，湖北 武汉 430074；2.武汉地铁集团有限公司，湖北 武汉 430030；3.新加坡南洋理工大学土木工程与环境学院，新加坡 639798)

0 引言

近年来，随着地下交通运输系统的迅猛发展，基于多节点传感器网络的地铁损伤识别及健康监测系统逐步得到应用，监测数据采集、传输、存储和处理成本的消耗是传感器网络系统搭建的一个关键性技术问题。传统的信号采集方法基于Nyquist采样定律，为了避免信号恢复的损耗，响应采集频率需大于原始响应最大频次的2倍，给数据的传输和存储带来沉重的负担，如何在保证重构精度的情况下尽可能地减少数据量是地铁健康监测系统数据采集与传输领域面临的新挑战。

随着信号采集重构问题的出现，Donoho[1]、Candes等[2]提出了压缩感知理论的基本原理，并将压缩感知理论分为信号稀疏化、选取测量矩阵和信号重构算法3个主要部分。其中，测量矩阵将稀疏信号从高维空间投影到低维空间上，解决了传统采样方法数据存储压力大、采样时间长的问题[3]。由于测量矩阵决定了采样信息的压缩性能与恢复质量，其构建成为了压缩感知研究的热点[4]。Bajwa等[5]提出构建Toeplitz随机矩阵，简化了测量矩阵的结构和尺度。赵贻玖[6]对随机等效采样技术的随机相位产生机制进行了分析。Yang等[7]基于图像先验以及条件约束来设计最佳的自适应测量矩阵。Wu等[8]将测量的耦合值作为边界条件来求解Laplace′s方程，得出的自适应测量矩阵能够较好地平衡处理次数与处理精度。赵玉娟等[9]基于随机高斯矩阵稀疏系数的部分向量进行自适应变换，构建的测量矩阵使重构的信号有更高的精度。综上所述，合适的测量矩阵能够降低压缩感知的计算量，并能提高信号重构的精度，在研究压缩感知问题时，需要选择与信号特点相匹配的测量矩阵以提高计算效率。

信号重构算法是压缩感知3个主要部分的关键环节。目前主流的信号重构算法包括贪婪迭代算法、LS算法以及基于贝叶斯模型的重构算法[10]。贪婪迭代算法最早由Davis等[11]提出，随后针对提高计算速度和计算精度等执行性能成为了研究热点。Tropp[12]提出了正交匹配追踪算法。基于此，为了得到更快的计算速度，Gavish等[13]基于传统匹配追踪算法的初始参数，采用精简化推出分段正交算法，并运用于大数据领域的实际工程。与此同时，一些学者依据压缩感知稀疏重构模型将其转化为凸优化问题求得原始信号的近似解，基于此最早提出了基追踪算法[14]，同时也提出了稀疏梯度投影模型[15]、基于平滑L0范数的算法模型[16]、最小化L1范数求解稀疏模型[17]等重构算法。目前，压缩感知理论受到业界学者广泛的研究，研究方向涉及图像压缩重构[18]、声道信号处理[19]、检测报警系统[20]等信号大数据领域，但在土木工程行业应用涉及较少，方法也较为传统[21]，缺少针对运营隧道结构健康监测特点的压缩感知方法。针对运营隧道监测中大数据传感器网络监测量结构性差、盲稀疏度、高噪声干扰的特征，将压缩感知理论引入运营隧道结构健康监测中的数据采集和传输层，结合隧道工程运营期监测数据的特征降低采样率，减少数据采集过程中的资源浪费和服务器无线传输负担。

本文研究基于传统单节点压缩感知重构算法，引入传感器网络框架表示模型，对传统的压缩采样数据重构算法进行改进，转化为凸优化问题，用迭代方法求解最小化范数问题，提出基于传感器网络的压缩感知重构算法。以武汉地铁3号线王家湾至宗关区间(以下简称王宗区间)隧道采集的加速度信号为例，对提出的算法进行验证，对原始信号进行多层次采样，并采用传统单节点压缩感知重构算法和基于传感器网络的压缩感知重构算法进行信号重构，结果表明，基于传感器网络的压缩感知重构算法在一定采样率条件下可以有效增加数据恢复的精度。

1 面向运营隧道结构健康监测预警系统大数据压缩感知

1.1 传统单节点压缩感知重构算法理论

当前运营隧道健康监测系统中远程传感器网络受计算能力较差、传输带宽低、要求实时传输等条件的限制，大都采用基于Nyquist采样定律的传统信号采集传输方法处理监测数据。传统信号采样压缩过程包括原始信号采样、量化、压缩编码、信号重构。随着压缩感知的提出，信号采集处理的过程变为稀疏变换、编码测量和信号重构。传统信号采样压缩需要对信号均匀抽样，再对采用的信号量化编码压缩降低信号冗杂。压缩感知的核心是线性测量，压缩过程即采样过程，通过少量的采样信号得到精准的重构信号，降低全过程数据库的运载消耗。传统压缩感知研究主要从信号稀疏化、选取测量矩阵、信号重构算法3方面展开。

1.1.1 信号的稀疏变换

信号的稀疏变换反映的是信号的稀疏性，信号稀疏性定义如下：

假设向量u∈Rm有k个非零元素，且满足k≪m，则u为R上稀疏度为k的稀疏向量。

设有1个一维信号x∈Rn,该信号可以用1组正交基ψ=[ψ1,ψ2,…,ψn]进行线性表示，表达形式如式(1)—(3)所示。

(1)

αi=〈x,ψi〉或α=ψTx。

(2)

ψ=[ψ1,ψ2,…，ψn]。

(3)

式(1)—(3)中：x为原始一维信号；αi为正交基下的分解系数；ψ为信号x∈Rn的正交变换基。

如果x的分解系数αi中有k个非零元素，则信号在ψ正交基上是稀疏的，这也是数据可以被压缩采样的基础，信号稀疏性的不同将在很大程度上影响重构信号的精度。一般来说，结构健康监测过程中采集的信号本身不具有稀疏性，但采集的振动信号可以在某几组变换基下线性展开，如果变换基线性表示系数仅有少量非零值或是忽略不计的系数，在某种程度上也可以称信号在相应的变换基上具有稀疏性。信号的稀疏性是信号压缩采用的前提，信号稀疏性越好，振动信号的压缩采样结果越好，最终重构信号精度越高。

1.1.2 测量矩阵的构建

压缩感知是取1个不同于ψ正交基的测量矩阵Φ∈Rm×n，将稀疏信号x从N维空间通过线性投影到M维空间当中，其中M≪N，最后得到1个投影后的测量值，联合式(4)，过程如下。

y=Φx或y=Φψα。

(4)

式中：y为投影后的测量值；Φ为测量矩阵。

为了使测量值更多地保留原始信号的有效信息，令θ=Φψ,θ需要满足约束等距性(RIP性质)，即稀疏度为k的原始信号x，如果测量矩阵满足以下关系，则信号x满足RIP性质。

(5)

式中δk为等距常数。

矩阵RIP性质的运用虽然保证了测量矩阵的有效性以及较高的重构信号精度，但是验证矩阵是否满足约束等距条件需要复杂的计算过程。为简化问题，根据Candes等[22]提出的可利用观测矩阵Φ和稀疏基矩阵Ψ的非相关性代替RIP性质判断观测矩阵的构建。

其中对于N×M随机测量矩阵，满足式(6)可认为满足RIP性质。

M≥K·log(N)。

(6)

式中K为原始信号稀疏度。

稀疏变换基矩阵Ψ和测量矩阵Φ是否能够相互表示，可通过式(7)的计算结果大小判定。

(7)

式中：φk为测量矩阵Φ的第k行行向量；ψj为正交矩阵Ψ的第j列列向量。

式(7)表达了矩阵Ψ和矩阵Φ的关联性，算得的u值越小，表明矩阵Ψ和矩阵Φ两者越不相关，所得投影后测量值的有效信息越多，重构误差越低。一般地，无论稀疏基矩阵怎么变化，随机矩阵与任意一个确定的矩阵都具有较大的不相关性，因此，随机测量矩阵被广泛地运用于压缩感知，常见的随机测量矩阵主要有随机高斯测量矩阵和随机伯努利测量矩阵等。

1.1.3 信号的重构算法

θ矩阵在满足RIP准则的前提下，通过求解式(2)可以得到稀疏系数，将N维原始信号x从M维投影测量值y中重构出，只需要求解以下欠定问题的最优稀疏解来得出。

(8)

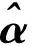
求解式(8)是一个线性规划求解凸优化问题的过程，L1范数最小化优化求解成为基追踪算法，本文传统压缩感知将采用常用的梯度投影法和内点法进行信号重构。传统的信号重构算法还有贪婪算法和贝叶斯框架算法。

1.2 结构健康监测大数据传感器网络

在监测系统数据传输层与储存层中，传统监测数据的重构将单个传感器节点重构，但因为结构监测测区内涉及多个测点，依据测点间的显著相关性与相似发展趋势布设相应传感器网络，如图1所示。

图1 无线传感器网络传输示意图

在运营隧道大型结构中，无线传感器网络分布在每个测区的传感器节点数较多，每个远程传感器具备独立采集、计算、传输通信能力。传感器网络类属于全分布式节点网络，每个传感器节点监测数据具有偶然性。对于大规模复杂问题，为了获得监测区段最接近实际的监测数据，以期分析出精准的健康状态结果，需要最大程度地发挥传感器节点之间的协同能力。运营隧道健康监测系统中需要改变传统单一的数据传输方式，采用簇头节点到终端的传输，簇头的选择对应了每个测区的传感器网络。

进行运营隧道结构健康监测时，无线传感器网络中部分传感器的采集频率大，1 d内单传感器监测的数据达百万级，加上测区均匀分布有多个传感器，两两之间的监测数据存在冗余，而基于传感器网络的压缩重构可以解决数据采集量极大、传输压力大的问题。通过压缩采集对测区传感器网络协同融合，将融合数据进行测量编码转入簇头节点传输到终端，在终端实现监测数据的重构。

综上所述，建立了基于传感器网络的压缩感知重构算法的理论框架。一般来说，传感器网络每个测区的传感器具有独立稀疏性，传统做法对每个监测信号进行稀疏变换，将稀疏变换系数传输到簇头节点进行编码测量，最终传输到终端设备。本文基于信号的独立性和相关性建立网络式的稀疏变换，对稀疏网络进行编码测量，解决单个传感器节点的数据冗余以及处理次数的问题。

1.3 面向大数据的基于传感器网络的压缩感知重构算法

1.3.1 传感器网络联合稀疏表示

传感器网络联合稀疏表示即将所有的传感器节点监测数据整合进行稀疏变换。假设运营隧道相邻断面有K个传感器节点，每个传感器节点在相同时间点tj同时采集1次数据，其中j=1,2,…,N，采样时段为[0,t]，采样频率T=N/t,原始采集的信号矩阵N×K用U表示，如式(9)所示。

(9)

式中UNK为第K个传感器节点N的监测数据值。

相较于传统监测采集技术，压缩感知无须遵循Nyquist定理，实际采集的信号为残缺矩阵。假设有集合Ω={(N,k)}以及置零矩阵PΩ：RN×k→RN×k，则有：

Y=PΩU。

(10)

(11)

一般的监测信号在频域上呈现稀疏性，信号重构从测量信号Y中重构出原始矩阵U，可表示为

U=Ψ·u。

(12)

式中：Ψ为离散傅里叶矩阵；u为单节点测量矩阵。

为表现基于传感器网络的压缩感知重构算法的优势，体现算法的群稀疏性，求解X∈R时采用最小化范数的形式书写，采用Tikhonov法解决正则化问题，即式(12)可变换为

(13)

式中：μ为正则化参数；Z为正则化约束。

1.3.2 采用Split Bregman求解凸优化问题

Split Bregman迭代算法类属于图像恢复前沿科学的算法，对大型多维数据的重构具有迭代速度快、重构精度高的优势，具体的求解原理如下。

以下定义Bregman距离。假设泛函J在u点的子梯度为J(u)且u∈X(X→R)，p点是其对偶空间中的某一点，即对于u，v∈X(X→R)和p∈∂J(u)，则Bregman距离定义如式(14)所示。

(14)

基于Bregman距离，将式(14)转化为无约束的优化问题，如式(15)所示。

(15)

式中φ(u)、H(u)为凸函数且在u处可微。

令d=φ(u)，代入Bregman距离，可以得到

(16)

式中λ为控制参数。

依据Bregman迭代算法和Bregman距离，可以得到

(17)

(18)

(19)

将式(17)—(19)展开，可得到

(20)

(21)

1.3.3 凸优化求解的迭代过程

本文引入凸优化理念，通过迭代方法求解式(13)。

1)初始条件：k=0，u0=0，b0=0；2)选择合适的收敛参数τ；3)按以下过程进行迭代求解，即通过Split Bregman迭代公式可以得到。

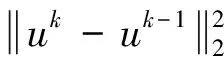
(22)

基于传感器网络的压缩感知重构算法采用迭代法寻找最优解，能够在一定程度上保证算法的收敛。与此同时，基于传感器网络的压缩感知重构算法原理将同一测区相邻多个测点传感器网络数据稀疏化集合进行重构，充分利用了监测信号的相关性特征。

2 基于大数据传感器网络的压缩感知重构算法实例分析

2.1 工程概况

湖北省武汉市地铁3号线于2015年12月28日正式运营，其中王宗区间右线里程起点DK9+996.728，向宗关方向大概延伸300 m，区间经过王家湾中心商业区和购物休闲广场。区间隧道为2条外径为6.2 m的左右双线隧道，隧道左右线间距为13～18 m，盾构隧道埋深14～41 m。根据地质勘探资料，隧道所在区间土质分布情况从上到下依次为杂填土、黏土、粉质黏土、粉土、粉质黏土、粉砂互层、粉细砂，运营隧道赋存土层段为粉砂互层与粉细砂层之间。

监测点与传感器网络布设图如图2所示。在运营隧道结构健康监测系统中，本监测项目实际采用6个加速度传感器监测隧道6个断面，分别命名为1—6号传感器，传感器采集频率为50 Hz，单次采集时间为30 min。

图2 监测点与传感器网络布设图(单位：m)

2.2 信号压缩采样及重构

为保证数据的相关性且具备一定量试验组的要求，选取1个测试区6组传感器(1—6号传感器)数据作为研究对象，取每单次监测的10 000个检测序列进行研究。图3示出1—6号加速度传感器信号时程图，可以看出6个加速度传感器测得的数据都较为平稳，幅值波动较为近似，相关性较大。

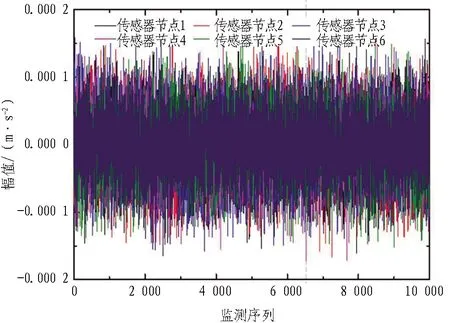
图3 1—6号加速度传感器信号时程图

基于传感器网络的压缩感知重构算法针对相同测区传感器网络在相邻测点的传感器节点监测信号在频域幅值有稀疏相关性，通过对原始信号矩阵进行傅里叶变换提取频域信号。1—6号加速度传感器信号傅里叶变换图如图4所示。可以看出6个传感器节点在频域幅值呈现高稀疏相关，信号重构效果更加精准。为更直观地反映传感器网络的相关性，用 Pearson 相关系数来表达监测信号之间的相关性，计算公式如式(23)所示。

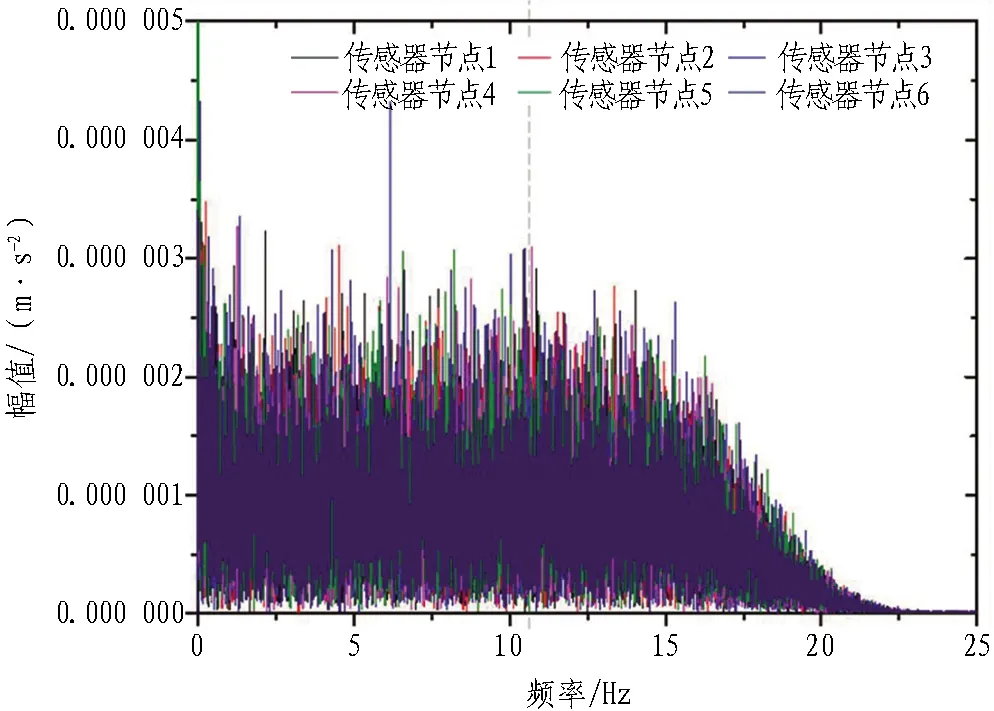
图4 1—6号加速度传感器信号傅里叶变换图

(23)

式中：A、B为监测数据；i为传感器节点号；C为相关系数。

通过计算传感器网络6个传感器节点监测信号两两之间的相关系数，得出监测信号之间在频域的相关系数C集中在0.732～0.891，原始信号矩阵各传感器节点之间有强稀疏相关，满足群稀疏化的特征，传感器网络算法重构结果更加精确。

本节对采集的加速度响应信号进行传统单节点压缩感知重构算法和基于传感器网络的压缩感知重构算法处理，取传感器节点1不同采样率数据时域幅值重构结果和误差，如图5—11所示。

(a)传统单节点压缩感知重构算法 (b)基于传感器网络的压缩感知重构算法

(a)传统单节点压缩感知重构算法 (b)基于传感器网络的压缩感知重构算法

由图5—11可以发现：对于传统单节点压缩感知重构算法和基于传感器网络的压缩感知重构算法，数据采样率越大，数据重构精度越高；相同采样率条件下，基于传感器网络的压缩感知重构算法的重构精度要大于传统单节点压缩感知重构算法。

2.3 信号重构误差分析与健康监测应用验证

2.3.1 误差分析

压缩感知数据的压缩采集到恢复重构针对不同数据特征类型有相应的适用性和精准性。由图5—11可知，基于传感器网络的压缩感知重构算法总体比传统单节点压缩感知重构算法重构精度高。相较于图11信号均方根误差，为更直观地获得传感器网络矩阵误差，以分析2种重构算法在采样率因素下的重构精度，引入范数误差，如式(24)所示。

(24)

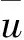
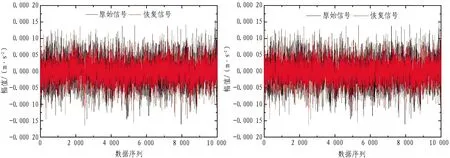
(a)传统单节点压缩感知重构算法 (b)基于传感器网络的压缩感知重构算法

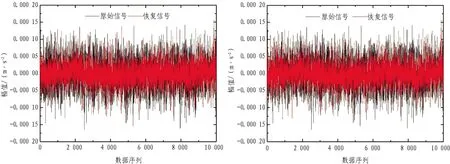
(a)传统单节点压缩感知重构算法 (b)基于传感器网络的压缩感知重构算法

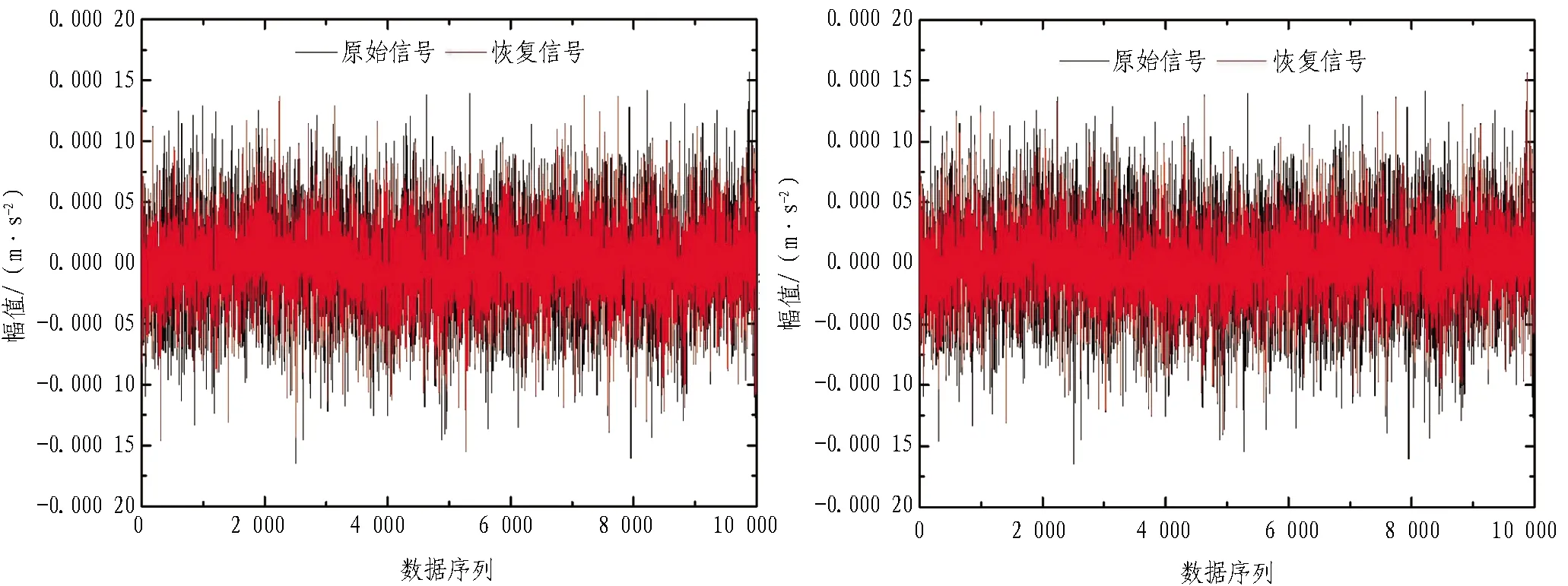
(a)传统单节点压缩感知重构算法 (b)基于传感器网络的压缩感知重构算法

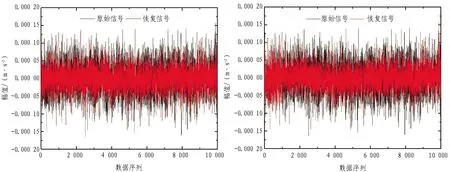
(a)传统单节点压缩感知重构算法 (b)基于传感器网络的压缩感知重构算法

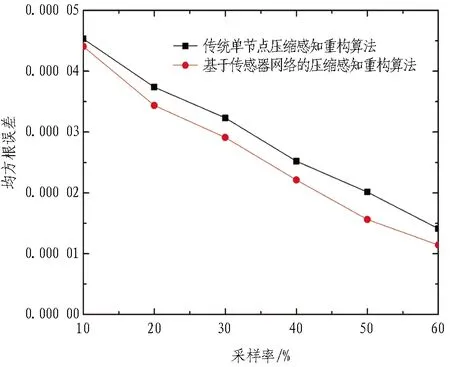
图11 传统单节点和基于传感器网络的压缩感知重构算法时域幅值重构结果均方根误差

表1为传统单节点和基于传感器网络的压缩感知重构算法在时域幅值的重构误差。可以看出：由于监测信号类型、特征与结构性因素，每个传感器节点在时域幅值上的重构精度不一。随着采样率增加，监测信号重构精度增加。相同采样率条件下，基于传感器网络的压缩感知重构算法的重构精度更高，表明基于传感器网络的压缩感知重构算法可以有效增加信号重构精度。在实际运用中，选取更大的采样率可以恢复到更精确的重构信号。

表1 传统单节点和基于传感器网络的压缩感知重构算法在时域幅值的重构误差

2.3.2 运营隧道结构健康监测系统应用验证

在实际运营隧道健康监测中，一般采用加速度频谱数据进行隧道健康评价，因此需要对原始信号和重构信号进行傅里叶变换，转换为频域数据后再对比重构误差。表2为传统单节点和基于传感器网络的压缩感知重构算法在频域幅值的重构误差。

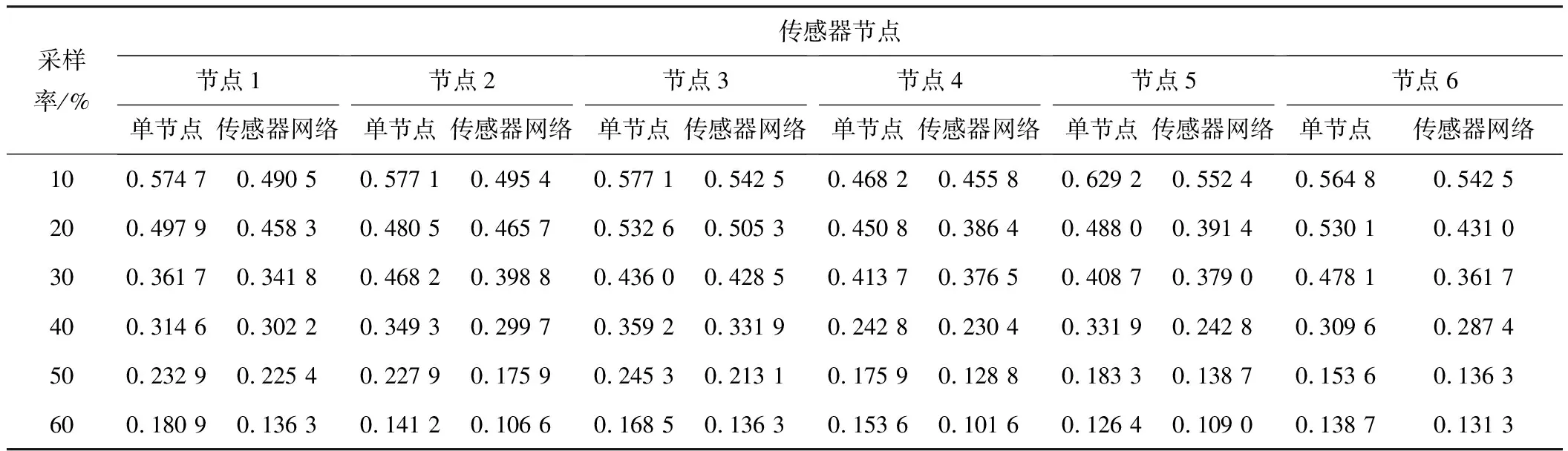
表2 传统单节点和基于传感器网络的压缩感知重构算法在频域幅值的重构误差

由表2可以看出：对于加速度信号时域幅值规律性弱、频域幅值规律性强的信号，其频域幅值的重构误差更小；相同采样率条件下，基于传感器网络的压缩感知重构算法的重构精度比传统单节点压缩感知重构算法高；随着采样率增加，2种方法的重构精度提高，基于传感器网络的压缩感知重构算法精度提升更为显著。

本监测项目监测的加速度信号有盲稀疏度、高噪声干扰以及结构性弱的特征，在低采样率下重构的时域幅值误差偏大，随着采样率增加，误差有所减小。基于传感器网络的压缩感知重构算法依据传感器数据结构的相似性，重构误差有所减小。在实际工程应用过程中，要保证监测预警的准确性，采样率为60%以上，均方根误差为1.06×10-5，式(24)误差为0.193，总体误差在20%以下，达到工程应用标准。

2.3.3 传感器网络节点数量耦合效应研究

为了研究传感器网络中节点数量对于信号压缩重构的影响，将断面加速度传感器的数量增加到了10个，并对不同采样率和传感器节点数量下的重构精度进行了计算。图12示出采样率为10%～60%、传感器网络节点为1～10个的时域幅值重构误差。可以看出，基于传感器网络的压缩感知重构算法中传感器的个数及监测断面、断面布设传感器的数量对重构误差也有影响，传感器网络矩阵中传感器节点数对最终信号重构时(频)域幅值的误差有不同程度的影响。

由图12可以看出：随着监测信号采样率增加，加速度响应在时域幅值的重构误差下降，恢复信号精度增加；随着传感器网络节点数的增加，相同采样率条件下，整体的恢复信号重构误差均有不同程度的下降；当传感器节点增加至6个以后，曲线趋于收敛，重构误差不再有明显下降，表明在基于传感器网络的压缩感知重构算法中，针对不同类型、特征、结构性监测信号，存在一个耦合上限。本研究的加速度传感器的监测耦合上限为6个，超过这个数值后，重构精度没有明显变化。

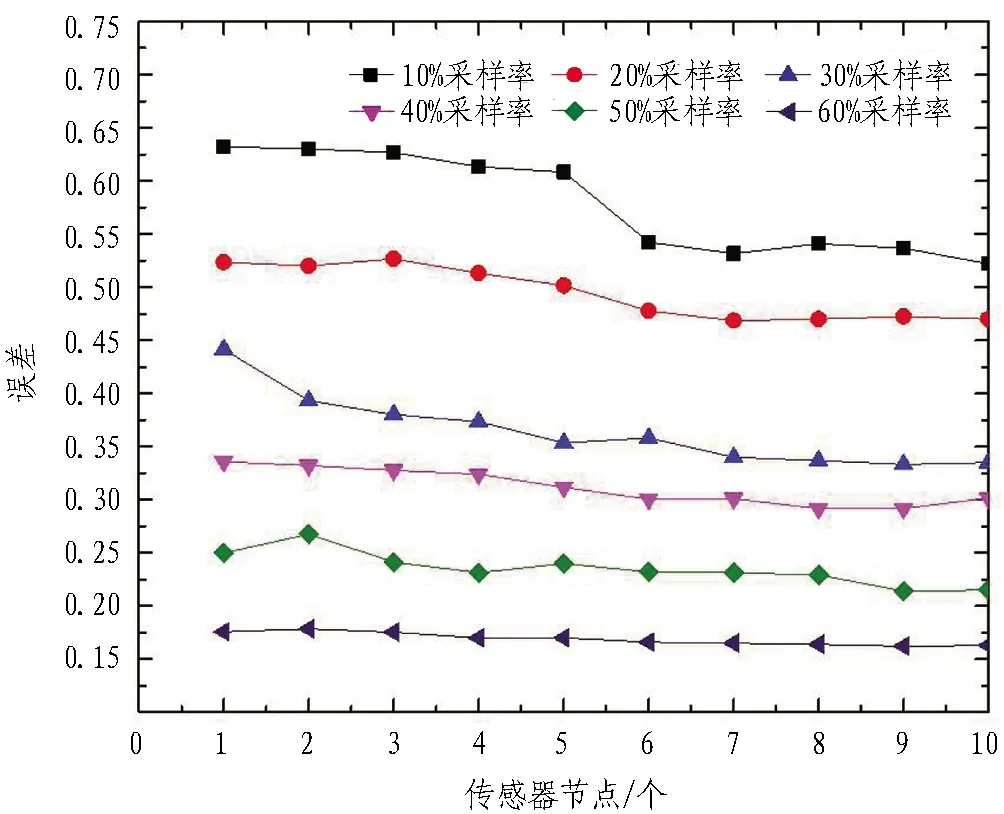
图12 时域幅值重构误差和传感器节点数量的关系

3 结论与讨论

1)本文基于传统单节点压缩感知重构算法，引入传感器网络框架表示模型，建立基于传感器网络的压缩感知重构算法，采用迭代方法求解最小化范数问题，具有很好的收敛性，可以得到比传统单节点压缩感知重构算法更精确的重构结果，压缩采样率为60%以上，总体误差在20%以下，符合工程应用标准。

2)针对不同类型、特征、结构性监测信号，基于传感器网络的压缩感知重构算法存在一个耦合上限。本文研究的加速度传感器的监测耦合上限为6个，超过这个数值后，重构精度没有明显变化。

3)本文只针对一种信号类型进行了试验，如果利用耦合性压缩算法对不同信号类型进行压缩重构可能会无差别过滤异常信号，导致不能正常反映隧道健康关键信息。下一步研究需要采取不同的压缩重构算法处理不同的信号类型，以实现多种信号的耦合压缩感知。