降低GFDM 峰均功率比的低复杂度算法

蔡建辉，李光球，沈静洁

（杭州电子科技大学通信工程学院，浙江 杭州 310018）

1 引言

广义频分复用（generalize2 frequency 2ivision multiplexing，GFDM）是一种灵活的多载波调制方案，具有较小的带外辐射、较低的时延、较高的频谱效率以及无须严格时间同步等优点，非常适用于物联网、触觉互联网和工业自动化等领域应用[1-4]。但是，GFDM 存在峰均功率比（peak to average power ratio，PAPR）较高的问题[5]，需要采取措施加以解决。

降低GFDM 系统PAPR 的方法大致可分为信号预畸变和信号非畸变两类。信号预畸变类包括限幅法[6]、分段非线性压缩技术[7]、改进型压扩技术[8]、多项式压扩技术[9]等。非畸变类包括预编码算法[10-12]、选择映射（selecte2 mapping，SLM）法[13]、部分序列传输法[14]、随机分配滤波器算法[15]等，其中预编码算法和SLM 算法较为常用。

预编码算法是通过降低信号的非周期相关性来降低系统的PAPR[12]，参考文献[10-12]分别提出用沃尔什－哈达玛变换（Walsh-Ha2amar2 transform，WHT）、加权分数傅里叶变换、离散哈特莱变换等来降低GFDM 系统的PAPR。SLM算法是将随机产生的多个相位序列与经过星座映射的频域信号进行点乘，之后经GFDM 调制，选择时域信号中PAPR 最小的GFDM 信号进行传输[13]。参考文献[13]通过引入相位旋转矩阵提出了修正的SLM 算法，其设计思想是要获得更多的GFDM 时域备选信号以降低GFDM 的PAPR。受上述设计思想的启发，若将预编码和SLM 算法联合应用于GFDM 系统，则预期可降低GFDM 的PAPR，为此需要求解串联的WHT 和离散傅里叶逆变换（inverse 2iscrete Fourier transform，IDFT）。参考文献[16]提出了正交频分复用（orthogonal frequency 2ivision multiplexing，OFDM）系统中可用T 变换实现串联的WHT 和IDFT 以降低其PAPR 和实现复杂度，本文将之推广应用于GFDM系统，于是提出了降低GFDM 系统PAPR 和实现复杂度的TSLM 算法。

参考文献[17]提出在OFDM 系统中引入基于转换向量（conversion vector，CV）的SLM 算法，其中转换向量由两个基向量及其循环移位构成，该算法可有效降低OFDM 系统的PAPR 和实现复杂度。本文拟将CV 向量引入TSLM 算法，提出了TCSLM 算法，该算法利用CV 向量与GFDM时域信号循环卷积以产生更多的时域备选信号，从而降低GFDM 系统的PAPR。下面拟从实现复杂度和仿真结果两个方面证明 TSLM 算法和TCSLM 算法的有效性。

2 GFDM 收发信机及SLM 算法

2.1 GFDM 收发信机

GFDM 收发信机框架如图1 所示。输入比特流先经正交幅度调制（qua2rature amplitu2e mo2-ulation，QAM）得到长度为N=KM的QAM 调制信号矢量d，经串并变换形成M个子符号、K个子载波的数据块结构，其中，dk,m表示第m个子符号中第k个子载波上传输的数据符号，k=0,1, …,K−1,m=0,1, …,M−1。然后经过由IDFT 和上采样、滤波、循环移位、求和操作（简称UFCS 模块）等组成的GFDM 调制器得到N×1维的输出向量x，最后添加循环前缀（cyclic prefix,CP）并发送出去。输出向量x可表示为[12]：

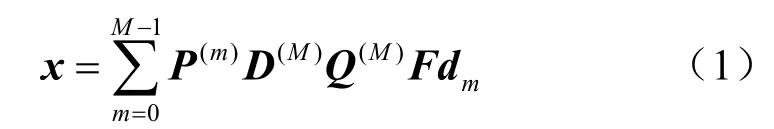
其中，dm=(d0,m,d1,m, …,dK−1,m)T表示第m个子符号，(· )T表示转置，F是K×K维的IDFT 矩阵；Q(M)由M个K×K维的单位矩阵IK串联而成，即Q(M)=[IK, …,IK]T，该操作可等效于对每个子符号进行M倍的上采样处理；D(M)是N×N维的滤波器矩阵，其对角线元素由升余弦（raise2 cosine filter，RC）滤波器g[n]组成，其余元素为0，g[n]的时域形式为g[n] =sinc(n)cos(παn)/(1 −4α2n)，其中，n=0,1, …,N−1，α为RC 滤波器的滚降系数；P(m)是N×N维矩阵，定义为P(m)=ψ(p(m))⊗IK，每个子符号通过P(m)变换到其对应位置，其中，⊗表示克罗内克积，ψ(p(m))是M×M维的循环矩阵，p(m)表示第m个位置的元素为1 而其余为0 的M× 1维向量，p(m)是ψ(p(m))矩阵的第一列，其余M− 1列是p(m)的循环移位。

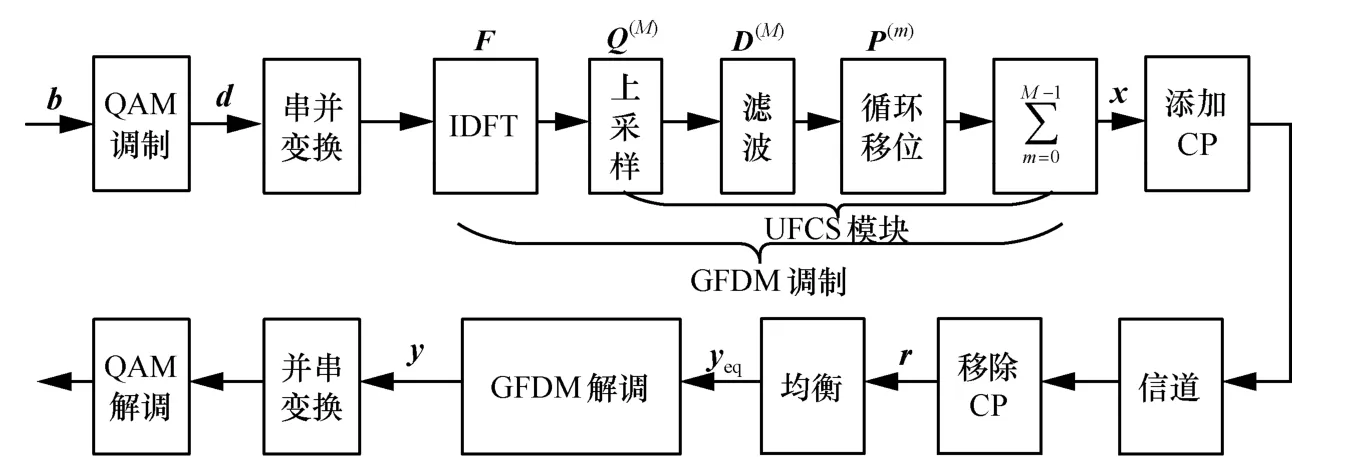
图1 GFDM 收发信机框架

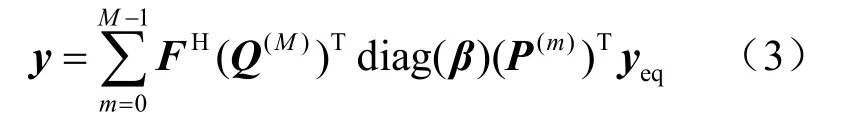
其中，2iag( · )为对角矩阵，其对角线元素为β[n]=1/g[n]，是迫零接收滤波器的脉冲响应；FH表示K×K维的离散傅里叶变换（2iscrete Fourier transform，DFT）矩阵。最后，经GFDM 解调的输出信号y通过并串变换和QAM 解调得到原始输入比特流的估值。本文GFDM 系统的参数、数学符号和矩阵函数的定义见表1。

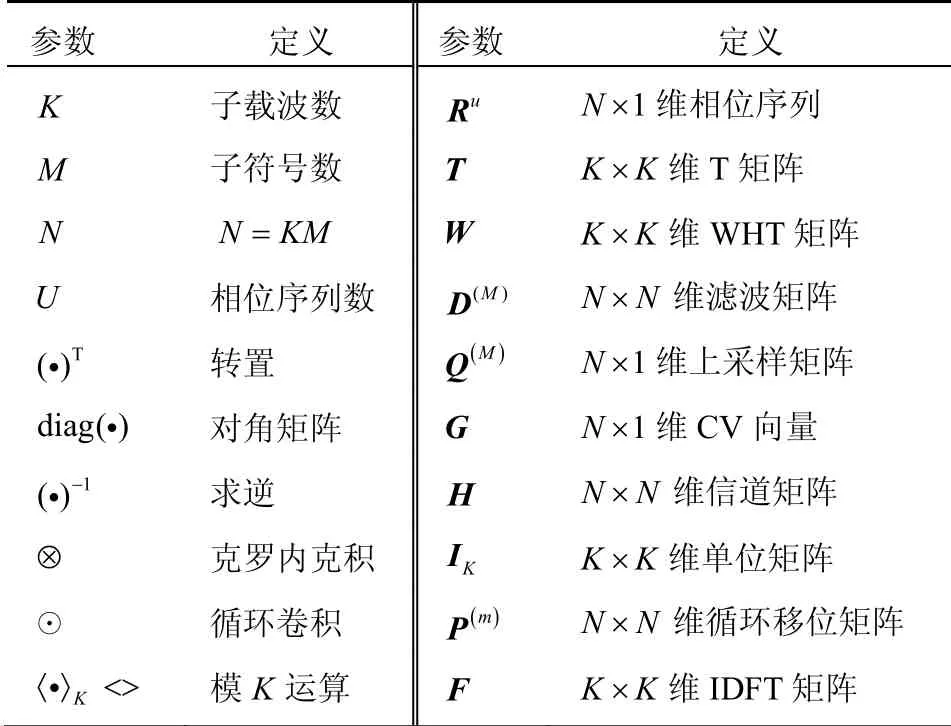
表1 系统参数、数学符号和矩阵函数的定义

2.2 SLM 算法

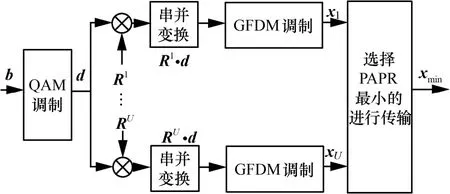
图2 降低GFDM 系统PAPR 的SLM 算法原理

3 改进的SLM 算法

3.1 TSLM 算法

WHT 变换能够有效降低 GFDM 系统的PAPR[10]，因此，本文将WHT 变换和SLM 算法相结合提出了一种改进的低复杂度TSLM 算法，如图3 所示，但在该算法中需要完成串联的WHT变换和IDFT 变换，计算相对复杂。经分析可知，参考文献[16]中用于OFDM 系统的T 变换可以实现本文中串联的WHT 变换和IDFT 变换，因此本文提出利用T 变换降低GFDM 系统的PAPR，同时利用T 变换的稀疏特性降低其实现复杂度。

低复杂度TSLM 算法的实现步骤如下：

（1）将QAM 调制信号与U个不同的随机相位序列UR进行点乘；

（2）将点乘后的U个信号进行串并变换；

（3）将串并变换后的信号依次通过T 变换和UFCS 模块完成T-GFDM 调制；

（4）从U个GFDM 时域备选信号中选择PAPR 最小的信号进行传输。

由参考文献[16]的式（9）可得以上步骤中T变换矩阵为：

3.2 TCSLM 算法

增加备选GFDM 信号可以降低系统的PAPR，本文在TSLM 算法的基础上引入CV 向量，提出了TCSLM 算法，其基本原理是将经过T-GFDM调制后的信号与CV 向量进行循环卷积，该操作增加了T-GFDM 时域备选信号数目，但没有增加系统的复数乘运算次数，原理如图4 所示。

TCSLM 算法的实现步骤如下：

（1）将QAM 调制信号与U个不同的随机相位序列UR点乘；

（2）将点乘后的U个信号进行串并变换；

（3）对串并变换后的信号进行T-GFDM 调制；

（4）T-GFDM 调制后的信号通过CV 向量，此时时域备选信号的个数为2U；

（5）从2U个时域备选信号中选择PAPR 最小的信号传输。

图3 降低GFDM 系统PAPR 的TSLM 算法原理

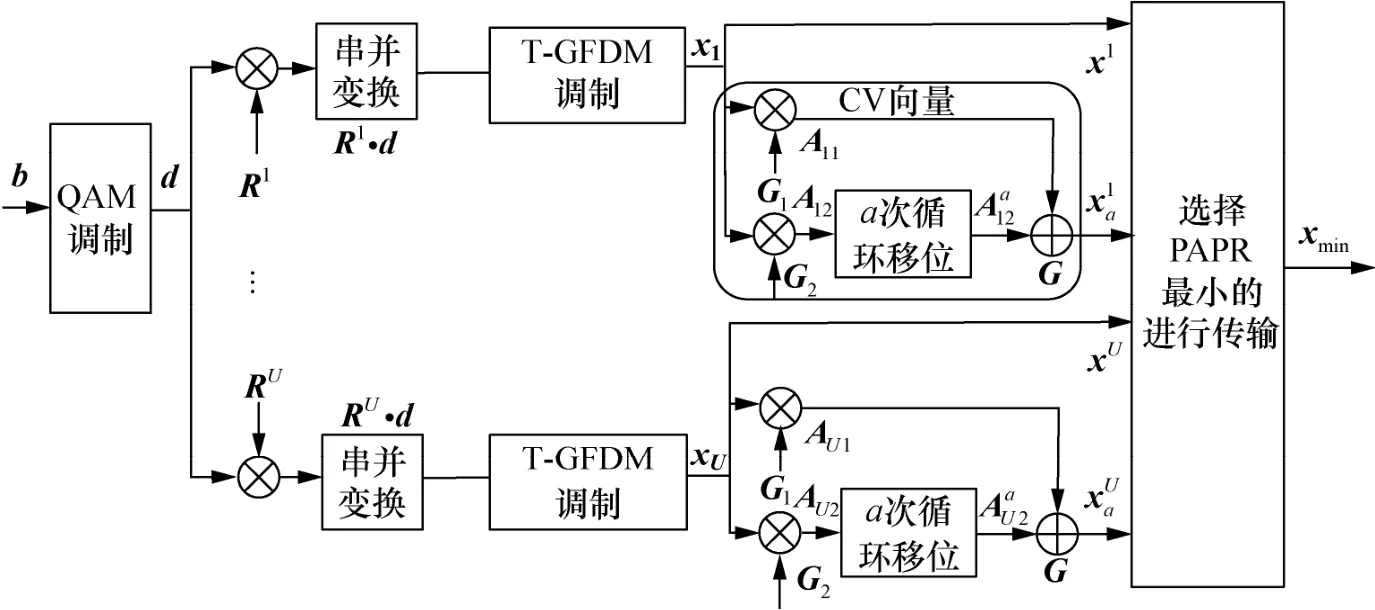
图4 降低GFDM 系统PAPR 的TCSLM 算法原理

根据循环卷积的线性性质，经过CV 向量而生成的GFDM 时域备选信号可表示为：

4 性能分析

4.1 实现复杂度分析

本节对采用SLM、WHT-SLM、TSLM 和TCSLM 算法的各GFDM 系统进行发射端复数乘法和复数加法的复杂度分析。参考文献[12, 15,18-19]对GFDM 系统的实现复杂度分析均以复数乘法作为性能指标，故本文将复数乘法作为实现复杂度分析的性能指标。

根据式（1），图1 的GFDM 调制需要以下步骤：（1）M次K点的IFFT 变换，一次K点的IFFT 变换需要执行KlbK/2次复数乘和KlbK次复数加；（2）M次滤波，一次滤波需要执行KM/2次复数乘。因此，GFDM 调制的复数加次数J=MKlbK，复数乘次数C为[12]：

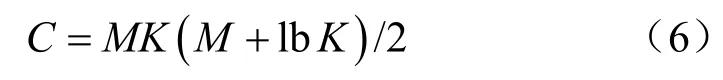
根据参考文献[16]，一次K点的T 变换需要执行的复数乘和复数加次数分别为(KlbK)/2 −(K− 1)和(3KlbK)/2 −3(K− 1)。图3中的T-GFDM 调制需要以下步骤：（1）M次K点的T 变换；（2）M次滤波。因此，T-GFDM调制的复数乘和复数加次数分别为C−M(K−1)和3J/2 −3M(K− 1)。

SLM 算法是利用U个随机相位序列产生U个频域备选信号，然后进行U次的GFDM 调制得到U个时域备选信号。因此，SLM 算法的复数乘和复数加次数分别为UC和UJ。

根据图2 和图3，TSLM 算法是在SLM 算法的基础上利用T 变换实现串联的WHT 变换和IDFT变换，而WHT 变换由于其元素由1 和−1 构成不会增加WHT-SLM 算法的复杂度，故WHT-SLM 算法的复数乘和复数加次数分别为UC和UJ。TSLM 算法需要进行U次的T-GFDM 调制，因此，TSLM 算法的复数乘和复数加次数分别为U[C−M(K− 1)]和3U[J/2−M(K− 1)]。4 种降低GFDM 系统PAPR算法的发射端实现复杂度比较见表2。

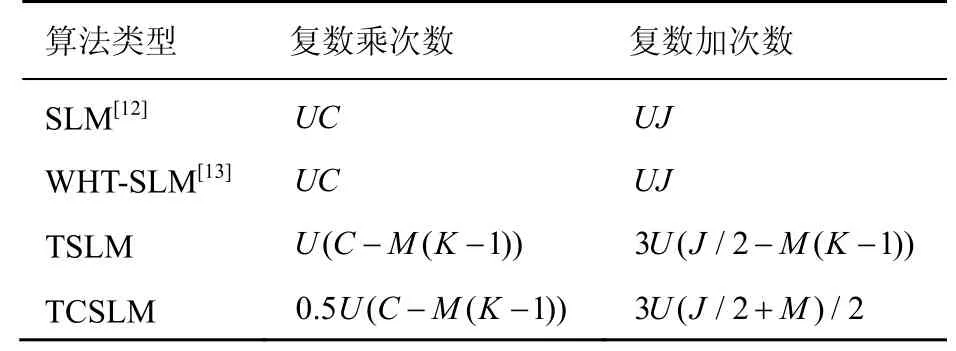
表2 4 种降低GFDM 系统PAPR 算法的发射端实现复杂度比较

根据图3 和图4，TCSLM 算法是在TSLM算法的基础上利用CV 向量得到了2U个时域备选信号，需要以下步骤：（1）U次的T-GFDM；（2）U个T-GFDM 调制信号与CV 向量循环卷积得到2U个时域备选信号，需要执行3UKM次复数加[17]。因此，TCSLM 算法的复数乘和复数加次数分别为U[C−M(K− 1)]和3U(M+J/2)，产生相同数量的备选信号，TCSLM 算法的复数乘次数是TSLM 的1/2。

4.2 仿真结果

本文通过计算机仿真比较采用上述4 种降低PAPR 算法的GFDM 系统性能。仿真参数设置如下：图5 中子载波数K取值为64～1 024，相位序列数U= 2 8、；图6 中取K=64，U= 2 8、；图7 中取K=64，U=2 ；其余参数均为子符号数M=3 ，RC 滤波器的滚降系数取0.1，调制方式采用16QAM，CP 长度取16。

图5 为GFDM 系统的实现复杂度（即复数乘法次数）随子载波数K的变化曲线，其中考虑了SLM、WHT-SLM、TSLM、TCSLM 4 种降低PAPR算法。由图5 可知：

（1）随着相位序列数增加，不同算法的复杂度随之增加；

（2）当不同算法的GFDM 系统的随机相位序列U取相同值时，算法复杂度排序由高到低依次是SLM（或WHT-SLM）、TSLM、TCSLM 算法，当K=64 、U=2 时，SLM（或WHT-SLM）算法、TSLM 算法和TCSLM 算法的复数乘次数依次为1 728、1 350 和675 次，与SLM（或WHT-SLM）算法相比，TSLM 和TCSLM 算法实现复杂度分别降低约21.9%和60.9%。

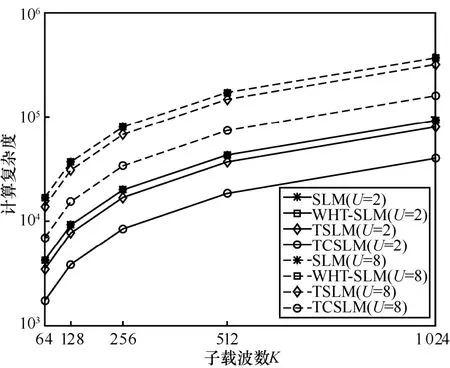
图5 不同算法的GFDM 系统复杂度对比

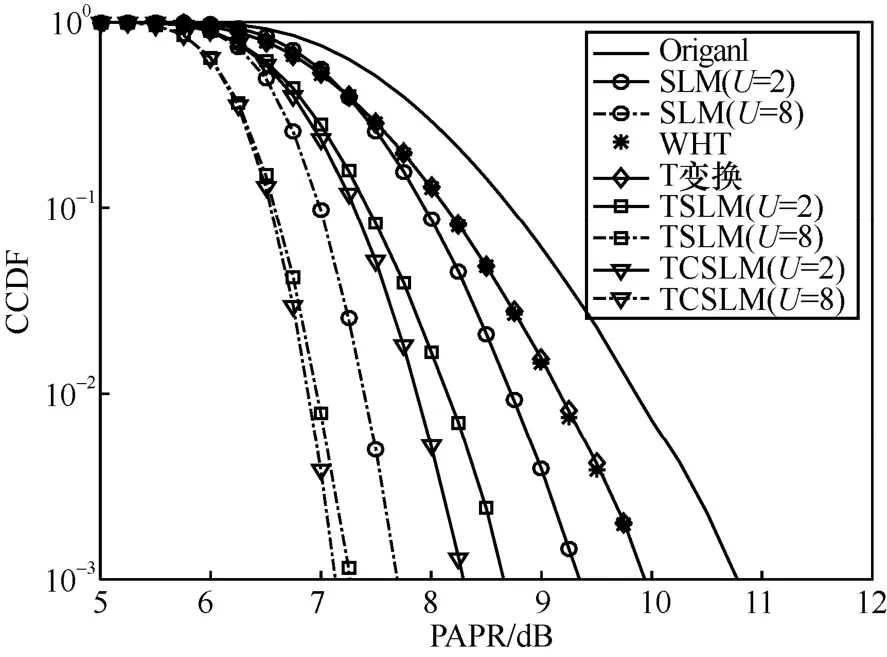
图6 不同算法的GFDM 系统PAPR 降低效果对比

采用不同算法降低GFDM 系统PAPR 的CCDF 性能曲线如图6 所示。由图6 可知：

（1）随机相位序列数U越大，SLM、TSLM和 TCSLM 算法降低 PAPR 的效果越好，当CCDF =10−3，相位序列数U=8时，采用SLM、TSLM 和TCSLM 算法的GFDM 系统PAPR 值比U=2时分别降低约1.6 2B、1.4 2B、1.2 2B；

（2）采用WHT 和T 变换的CCDF 曲线基本重合，结合表2 可知T 变换能够保持降低PAPR的效果并且降低复杂度；

（3）降低GFDM 系统PAPR 效果排序由强到弱排序依次是TCSLM、TSLM 和SLM 算法，如当CCDF =10−3，相位序列数U=2时，采用TCSLM算法的GFDM 系统PAPR 值比采用TSLM、SLM算法降低约0.4 2B、1 2B。

在频率选择性信道下采用不同算法的GFDM系统的误比特率（bit error rate，BER）性能曲线见图7，与参考文献[2]中一样，在仿真中设置L=16，由图7 可知以下结论。

（1）SLM 算法与原始GFDM 系统的BER 性能基本相同，这是因为SLM 算法将选定的相位序列作为边带信息进行传输[20]，接收机能够根据边带信息正确恢复出原始信号。如当SNR=12 2B 时，SLM 算法与原始GFDM 系统的BER 分别约为0.059 78 和0.059 72。

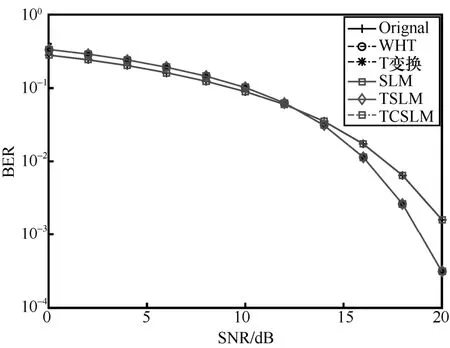
图7 不同算法的GFDM 系统BER 性能对比

（2）采用WHT 变换、T 变换、TSLM、TCSLM等算法的各GFDM 系统的BER 性能基本相同，这是因为T 变换实现了串联的WHT 变换和IDFT变换，可保持与WHT 变换基本相同的BER 性能[16]；TSLM 算法是在SLM 算法的基础上引入T 变换，接收机能够根据T 反变换和边带信息恢复出原始信号，因而TSLM 算法保持了与T 变换基本相同的BER 性能；TCSLM 算法是在TSLM 算法的基础上引入CV 向量，由于CV 向量的周期性自相关函数是冲激函数，其所有元素具有相同的大小，不会造成系统BER 性能的损失[21]，因此，TCSLM和 TSLM 算法的 BER 曲线基本相同。如当SNR=12 2B 时，WHT 变换、T 变换、TSLM 和TCSLM 算法的BER 分别约为0.062 72、0.062 60、0.062 68 和0.062 81。

（3）包含WHT 预编码算法的GFDM 系统能够有效对抗频率选择性衰落，但在低信噪比（SNR＜12 2B）下系统的BER 性能要劣于GFDM系统，这是因为ZF 解调引入的噪声分量在解码操作过程中对其他子载波造成了干扰[10]，低信噪比下该干扰对系统BER 性能的影响大于预编码方法改善效果。

综合图6 和图7 可知，TSLM 算法、TCSLM算法均能够有效降低GFDM 系统的实现复杂度和PAPR 值，同时基本不会造成其BER 性能的损失。

5 结束语

本文提出了TSLM 算法、TCSLM 算法降低GFDM 系统的PAPR，TSLM 算法的特点是利用T变换实现串联的WHT 变换与IDFT 变换，达到同时降低GFDM 系统PAPR 和实现复杂度的目的；TCSLM 算法是在TSLM 算法的基础上使用转换向量进一步扩充时域备选GFDM 信号的数目，从而进一步降低GFDM 系统的PAPR。计算机仿真结果验证了TSLM 算法和TCSLM 算法的有效性；在高信噪比下还能够改善GFDM 系统的BER 性能；增加随机相位序列U，可进一步改善GFDM系统的PAPR 性能，其代价是实现复杂度会略微增加。