高新技术企业研发成本的预测模型及方法探讨

刘 飒， 万 寿 义

(东北财经大学 会计学院，辽宁 大连 116025)

一、引 言

高新技术企业一般是指国家重点支持的高新技术领域内，持续开展研究开发与技术成果转化并形成核心自主知识产权的经济实体。区别于传统企业，高新技术企业具有风险高、投入大、收益好、成长快和竞争激烈等特点。新技术、新产品的研发和创造是高新技术企业发展的核心竟争力。相比欧美国家，我国高新技术企业起步较晚，但近年来创新力量持续增强，相应制度建设也在不断完善，高新技术企业在研发活动中的支出也呈现加速上升趋势，因此，提升企业创新能力、加快产业升级、加大成本管控力度、促进可持续发展已成为高新技术企业的当务之急和必然选择。随着国家创新驱动发展战略的不断推进实施，以及经济建设和社会发展对科技成果转化的迫切需要，企业研发成本的管理与预测正在得到越来越多学者的广泛关注和深入研究。

在成本管理方面，孙茂竹认为成本领先战略依旧是企业争夺市场、获取竞争优势的基本手段之一。企业必须借助有效的价值测量、控制和管理系统促进研发投入的有效利用，从而促进绩效的提升[1]。王迎迎基于研发项目的生命周期建立了成本管理模式，将研发成本划分为战略成本、风险成本、质量成本和目标成本4个管理阶段并分别开展成本研究[2]。Wang等人对资金来源与研发投入之间的关系进行研究，并通过实例表明了内生融资利率与研发投资之间存在正相关关系[3]。贺佳欢构建了研发成本管理模式，提出通过建立考核评价激励机制等途径提升研发成本管理效率[4]。李炳然分析研发费用核算与管理中存在的问题，提出了降低研发费用、提高研发效益的对策与方法[5]。梁莱歆等人考虑研发活动的不确定性及高风险性，将项目生命周期理论引入到研发成本管理中[6]。胡新武结合高新技术企业独有的特点，提出一种包括战略环境分析、战略规划、实施与控制、计量与评价4个方面的成本管理模式[7]。朱丹等利用激励相容的相关模型分析了高新技术企业研发预算管理及其创新绩效的关系[8]。Meng从内、外两方面找出影响高科技企业研发投入的因素，采用模糊综合评价方法进行因素筛选，最终提出了企业在不同场景下应采取的研发投资策略[9]。

在成本预测方面，李径路等人根据创业板企业的自身特点，引入径向基神经网络(RBF)和逆转传播神经网络(BP)进行研发预测[10]。陈会明指出成本预测的准确性将影响产品的成本，同时企业研发成本的诸多因素会影响成本预测的准确性,并将高技术企业研发成本预测视为由研发能力、生命周期、成本预测方法、新产品新技术增幅、外部环境5大子系统共同构成的一个系统，利用系统动力学理论建立了系统分析模型，给出了改进企业研发成本预测的措施[11]。李晓婉等人针对国内药业成本控制环节薄弱、目标成本不明确等问题，提出应建立成本预测体系，促使资金运营更为合理、研发动力更为强大[12]。Dimasi等人汇集10家制药公司共获得106种随机选择的新药的研发成本，利用这些数据估算了新药和生物制剂开发的成本问题[13]。

综上所述，现有文献针对高新技术企业研发成本管理和预测的研究较多，但由于研发成本涉及的因素较多，以及自身保密性、不确定性强的特点，为学者对研发成本预测研究带来较大困难。已有研究结果主要集中在阐述研发成本管理的意义、提出研发成本管理中的对策与方法等，主要关注有针对性的研发项目成本管理模式、以客户为核心的研发成本管理模式与多平衡点的研发成本管理模式，产生了一些有价值的研究成果。但从内容上看，研究者对成本管理和成本预测以模型与方法的角度加以系统研究的文献较多。从方法上看，多数文献对研发成本预测研究方法多为定性分析或定量研究，但将定性与定量相结合的研究方法较少。本文通过系统阐述高新技术企业成本特性与要素影响分析，运用主成分分析(PCA)提取关键影响因子，在此基础上运用支持向量机(SVR)方法对研发成本进行预测，进而分析其变化趋势，为企业未来经营与管理提供科学决策支撑。

二、高新技术企业研发投入特性及影响因素分析

1.高新技术企业研发投入特性

高新技术企业资本高度集中，知识与技术相对密集，具有高风险和高潜能等特征。这此特征决定了其研发投入不仅要满足产品、工艺的快速更新的需要，科技人才、创新环境不断变化的需要，还要适应提升竞争力和开展国际合作等迫切要求。因此，与一般企业相比，高新技术企业研发投入具有以下3种特性：

(1)投入高

高新技术企业中存在研发技术难度大、科技人才激励费用高、机器设备先进、试验测试研发活动频繁等特点。要保持企业可持续发展，需要不断加大投入力度，不断提高产品附加值，不断满足市场对产品的需要，保持竞争力。没有研究开发中的高投入就无法维持高新技术企业的发展。

(2)周期长

高新技术企业研发投入是一种持续性的投资，既存在初始投入，又需进行后续投入。为保证产品的市场占有率以及企业的竞争优势，高新技术企业需对产品及生产链利用科学技术最新成果持续寻求技术升级，一旦停止后续投入，前期的投入成果可能面临快速贬值甚至报废。因此，根据高新技术企业的行业特点与市场环境，研发投入需贯穿产品全生命周期。

(3)风险大

高新技术企业研发投入的高风险主要来自于技术不确定性与外部环境的多变性。由于高新技术企业产品技术复杂程度高、创新模式多样、更新换代较快、专业人才依赖度高等特点。同时，在研发的各环节中，高新技术企业还需面临市场风险、国家政策变化、财务风险等影响。因此，高新技术企业承担的研发风险较高于其他类型企业。

2.高新技术企业研发成本的影响因素分析

高新技术企业研发成本主要由新产品、新技术研发过程中产生的各项直接成本与间接成本构成。依据高新技术企业研发活动的特性，并结合企业发展轨迹、科技进步水平、地区经济发展、政策落实状况等实际情况，本文将影响高新技术企业研发成本预测的主要因素划分为研发能力、生命周期和外部环境3个重要因素。

(1)研发能力

高新技术企业研发能力是衡量企业新产品开发、新知识应用、技术能力强度、研发资本成果的标准，对企业研发成本产生重要影响。本文充分考虑企业研发资金投入强度、研发团队人员状况、新产品平均研发周期、成果转化情况、生产设备先进度、申请专利技术数、顾客满意度、产权制度明晰度、员工创新意识、企业协调能力等因素，在此基础上，本文确定选取团队科研技术水平(X1)和创新能力(X2)为研发能力的代理指标。

(2)生命周期

与传统企业相比，高新技术企业发展过程具有较强的阶段特征。在生命周期的不同阶段，企业的研发投入策略与经济效益存在较大差异。为了体现高新技术企业在生命周期各发展阶段的特点，本文考虑了企业在不同阶段投入成本的差异性、市场分析能力和企业实现发展目标能力，确定选取市场占有率(X3)、竞争者数量(X4)、市场规模(X5)、经营现金流量(X6)为生命周期指标。

(3)外部环境

高新技术企业与传统企业相比，其研发支出占企业总支出的比例较大，发生的直接成本费用相对较少，导致外部环境因素对高新技术企业影响程度较大。随着经济全球化，特别是在日益激烈的市场竞争现实环境、信息技术的有机融合以及顾客精细服务需求背景趋势下，高新技术企业更要注重对外部环境的科学分析，及时捕捉外部环境给企业带来的创新发展机遇。本文在充分考虑GDP变化、经济投资预测、物价指数水平、法律对行业限制程度以及自然环境变化等因素，选定通货膨胀率(X7)作为外部环境指标。

三、研究方法

高新技术企业研发成本预测涉及研发资金投入、创新转化能力、市场分析能力、企业发展目标能力、市场环境、竞争环境、监管环境等多方面内容，其内部构成及变化受内外界影响较大，因此，研究方法需考虑多变量并行处理、关键因素精准提取、跨维转化能力强、计算求解相对简单、预测精度高等因素，本文考虑将主成分分析和支持向量回归结合起来，实现对高新技术企业研发成本有效预测的目的。

1.主成分分析(PCA)

对高新技术企业研发成本预测，通过研究对比了类比估算法、参数估计法、全面详细估算法、软件工具法等预测方法。考虑到高新技术企业研发成本影响因素多、数据类型复杂以及多重共线等问题，本文采用主成分分析(PCA)对数据进行降维来简化数据结构，通过将多个指标合成为具有代表性的少数几个主成分实现降维，其中每个主成分所包含的信息各不相同，且能反映原始变量的绝大部分信息，在简化问题的同时，获得更加科学有效的数据信息。主要过程包括：

(1)将初始数据进行归一化处理，得到矩阵X。

(2)计算协方差矩阵R。

(3)求出特征值(λi)及特征向量(αi)。特征向量(αi)为主成分方差贡献率，反映了信息量的大小。

(4)计算主成分贡献率和方差的累计贡献率。

贡献率公式：

(1)

累计贡献率公式：

(2)

(5)选取主成分，满足特征值>1或方差累计贡献率>85%。

(6)计算主成分得分：

Fi=a1iX1+a2iX2+…+apiXp(i=1,2,3,…,m)

(3)

2.支持向量回归(SVR)

支持向量回归(SVR)是基于统计学的VC维理论和机构风险最小原理，把实际问题通过非线性变换转换到高维特征空间，在高维空间中构造线性决策函数来实现线性回归。由于选择不同的核函数可生成不同的SVR，降低了算法的结构风险。基于支持向量回归建立研发成本预测模型的主要思路为：

指定一个训练样本，其中，xi和yi分别代表SVR的输入和输出数据，假设f(x)=ω·Φ(xi)+b，Φ(x)为映射函数，b为偏置，ω为权重。

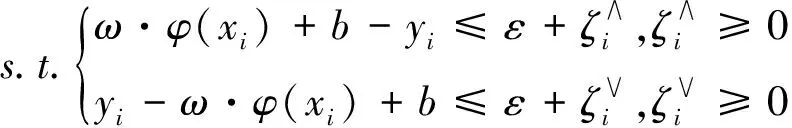
(4)

C为惩罚函数，C值越大说明数据的拟合度越好。ε为不敏感函数，ξi为松弛变量。引入a∧,a∨≥0为拉格朗日乘子，将原问题求解转化为对其对偶问题求解，K(xi,xj)=Φ(xi)·Φ(xj)为核函数，最终得到SVR模型如下：

(5)

3.PCA-SVR组合预测模型

基于企业研发投入是一个动态过程，本文构建了PCA-SVR组合预测模型对高新技术企业研发成本进行预测，其基本思路是：

(1)对样本数据进行离差标准化来消除指标变量在量纲上的差异。

(2)运用主成分分析法(PCA)对标准化之后的数据进行降维处理，提取影响企业研发成本的关键因子。

(3)将提取的因子作为SVR预测模型的样本数据，随机从中选取70%的样本作为训练集，30%的样本作为测试集，然后选取合适的SVR核函数和参数，建立SVR预测模型。

此方法将PCA的数据压缩和降维功能与SVR非线性建模能力有效结合起来，大大提高了预测的精确性。其结构如图1所示，其中X1，…，X7为输入层；PC1，…，PCk为隐藏层；w为输出层。此后通过实例开展对比测试和应用研究。

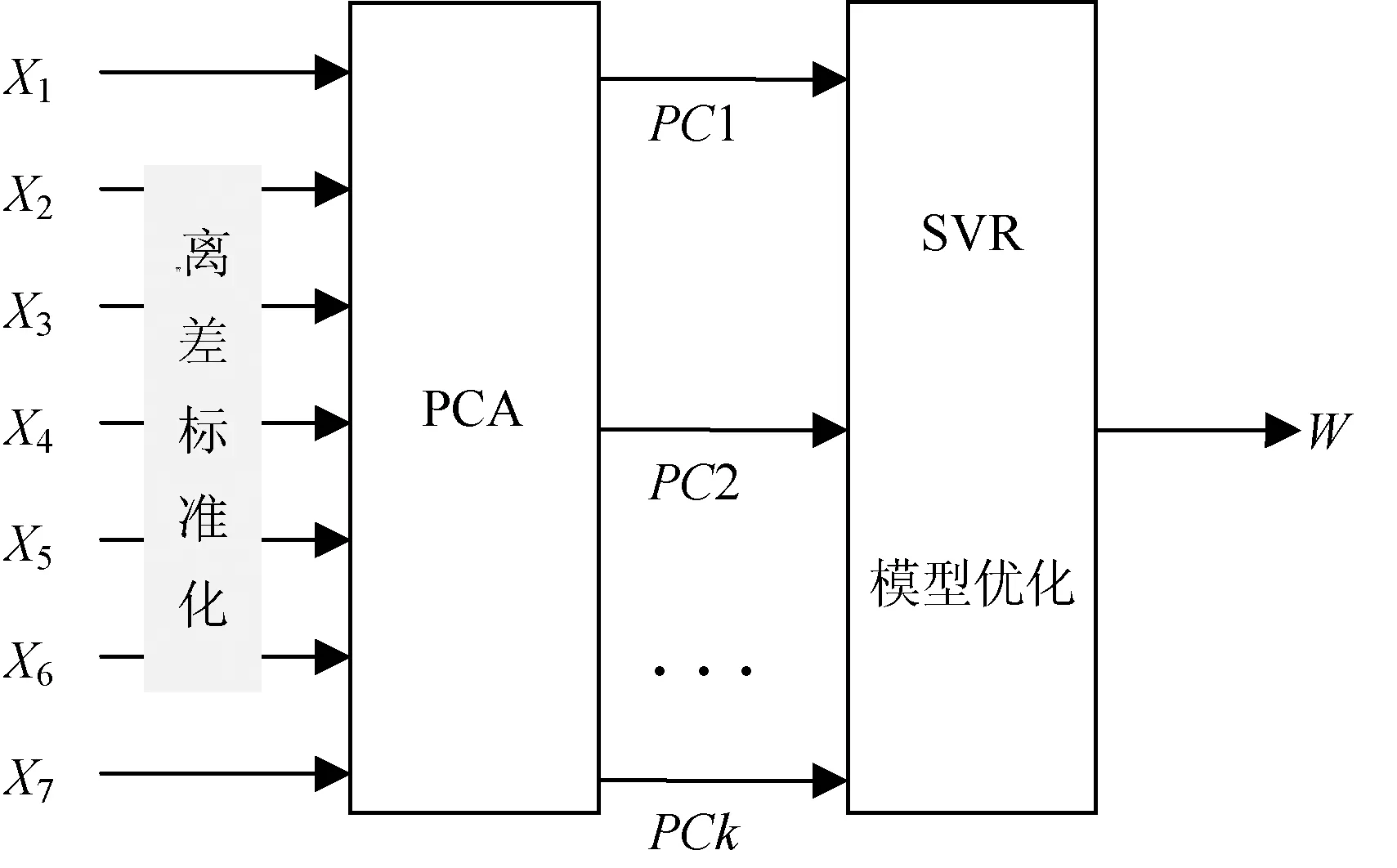
图1 PCA-SVR组合结构图

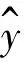
(6)

(7)

(8)

(9)

四、预测模型与应用

1.数据预处理

本文研究的数据集来自一家东北地区专业从事软件开发、软件定制、软件实施的高新技术企业——A公司，主要由57个案例组成，本文剔除不完整案例3个，最后得到54个完整案例。考虑到高新技术企业研发成本受到研发能力、生命周期与外部环境等方面的影响，选取以下数据：定性变量为团队科研技术水平(X1)、创新能力(X2)，通过专家评价法或德尔菲法得到数据；定量变量数据包括市场占有率(X3)、竞争者数量(X4)、市场规模(X5)、经营现金流量(X6)、通货膨胀率(X7)，可从A公司和国家统计局相关报告获得。

(1)离差标准化

由于研发成本各变量的性质不同，通常具有不同的量纲和数量级。当各变量间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的变量在综合分析中的作用，削弱数值水平较低变量的作用。因此，为保证结果的可靠性，需对原始变量数据进行标准化处理，公式如下：

(10)

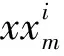
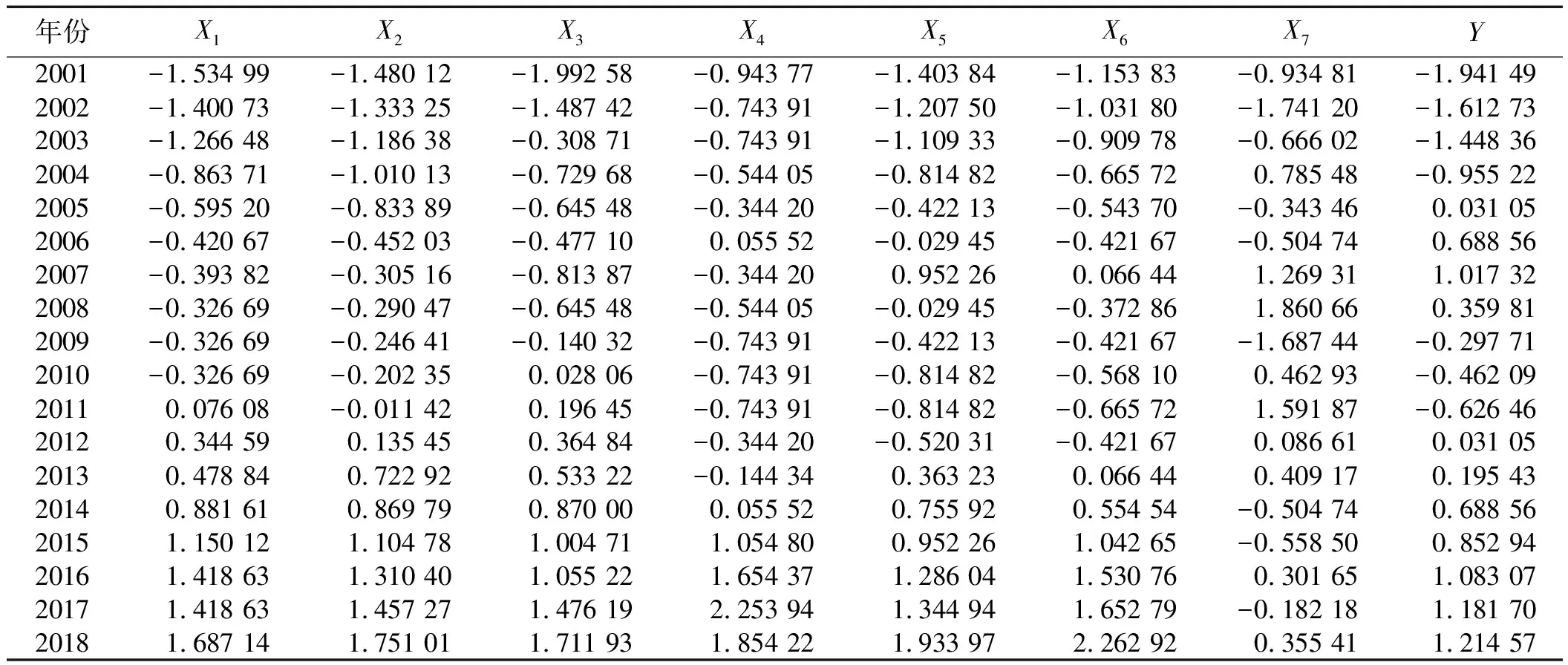
表1 离差标准化后的数据

PCA-SVR预测模型是对离差标准化后的高新技术企业研发成本进行预测的，因此需要对预测值进行还原，具体公式如下：

(11)

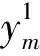
(2)降维

本文采用SPSS软件对离差标准化后的数据进行降维处理，提取影响企业研发成本的关键影响因子。在进行降维前，对7个指标进行相关性分析，检验指标间是否存在信息冗余。结果如表2所示。

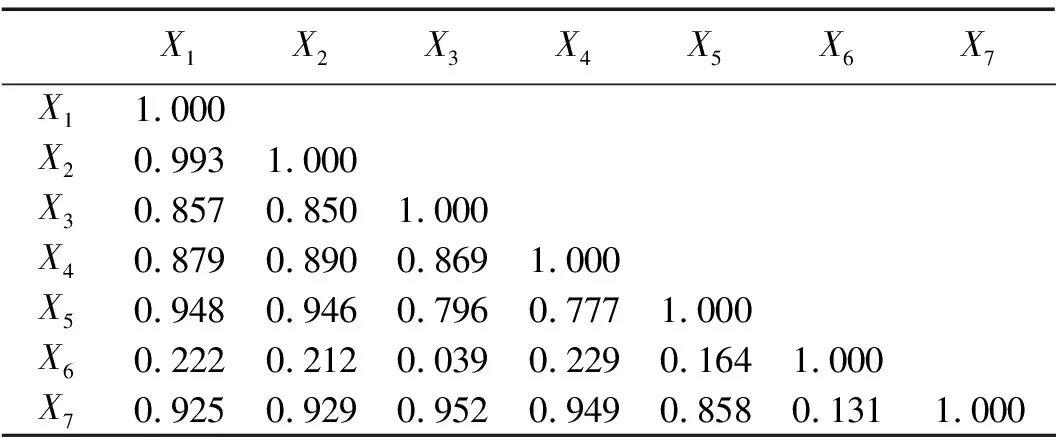
表2 特征值相关性矩阵

从相关系数矩阵可以看出，除了经营现金流量(X6)这一指标变量与其余6个指标变量相关性较低之外，其余6个指标变量间的相关系数均在0.85以上，表明企业研发成本影响因素间存在较强的相关性，则说明存在着大量的信息冗余。为定量分析样本特征的相关性，对样本数据进行了KMO检验及Bartlett球形检验，结果如表3所示。

表3 KMO 和Bartlett 检验

根据表中数据可知，KMO检验值为0.824(P>0.5)，Bartlett球形检验显著性水平为0.000(P<0.0001)，说明指标间信息重合程度较高。因此，有必要通过PCA方法对数据降维，消除指标变量间的信息冗余，简化预测模型，提高模型预测效率。

从表4可知，前4个成分的累计贡献率达到了99.116%，可以认为这4个主成分几乎包含了原始数据中的全部信息。因此，本文提取4个主成分，并对其分别命名为P1、P2、P3、P4，将表1中的数据代入表5中可获得7个影响因素提取主成分后的数值，将其作为SVR模型的输入数据，离差标准化后的研发成本为SVR模型的输出数据，如表6所示。

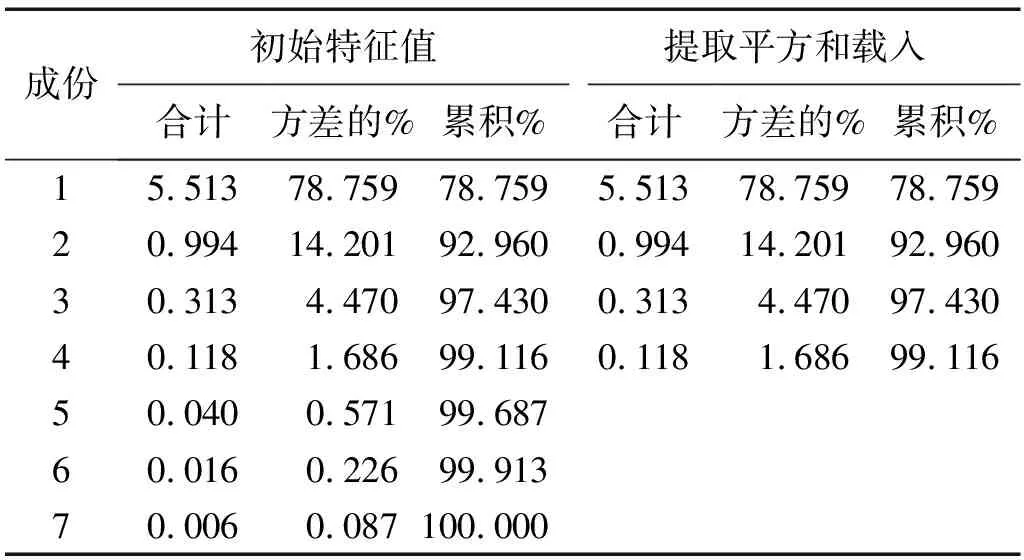
表4 主成分提取分析表

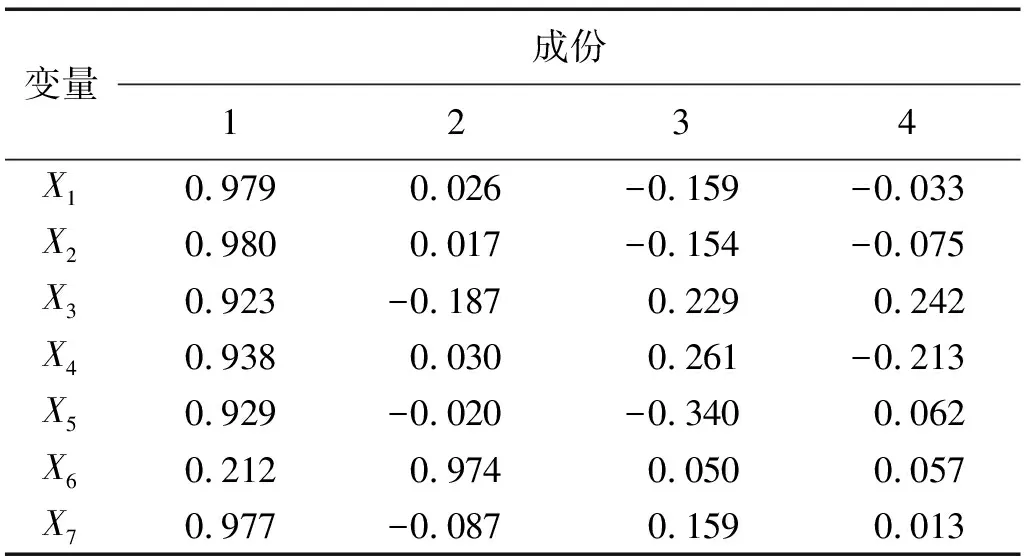
表5 初始因子载荷矩阵

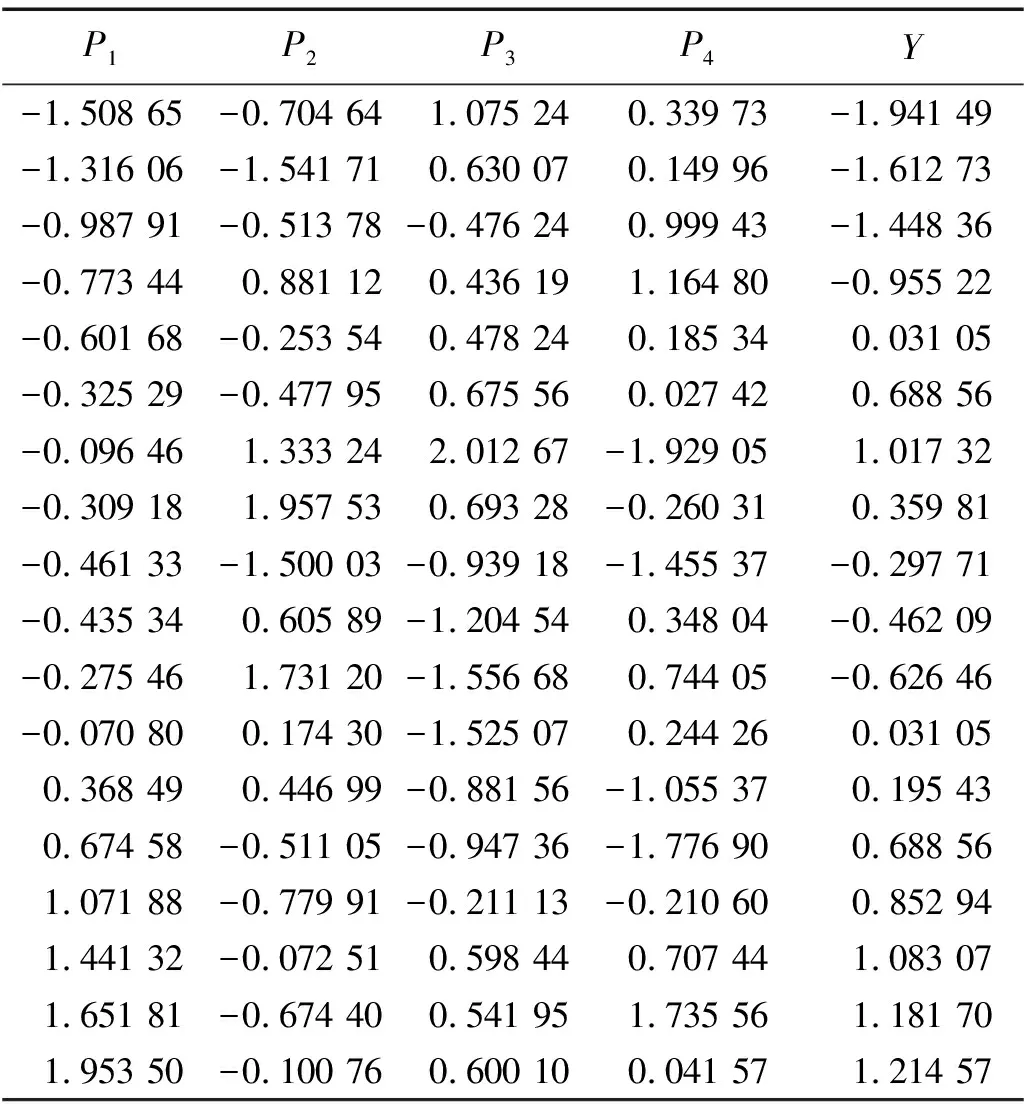
表6 提取主成分后的数据

2.模型优化

本文模型优化是指从线性核函数(Linear Kernel)、多项式核函数(Polynomial Kernel)、径向基核函数(Radial Basis Function)3种核函数中选择出最适合样本数据结构的核函数以及相对应的核参数来进行预测。其主要思路为在某种规则下将原始数据分为训练集和验证集，首先利用训练集对分类器进行训练，然后通过验证集对训练得到的模型进行测试，分析分类器的性能指标。

LinearSVR：

K(xi,xj)=xi·xj

(12)

PloySVR：

K(xi,xj)=(γxi·xj+r)d

(13)

RBFSVR：

K(xi,xj)=exp(-γ‖xi-xj‖2)

(14)

本文使用K—折交叉验证，其基本思路是在某种规则下将原始数据分为训练集和检验集，首先利用训练集对分类器进行训练，然后通过验证集对训练得到的模型进行测试，分析分类器的性能指标。该方法可有效避免欠学习和过学习的状态发生，得到的结果具有科学性。

采用交叉检验的方法对3种不同核函数的SVR模型进行评估，当采取径向基核函数时，(惩罚因子C=100，参数gamma=0.1)，SVR模型评分最高，结果如图2所示，因此，SVR模型采用径向基核函数，C=100，gamma=0.1。

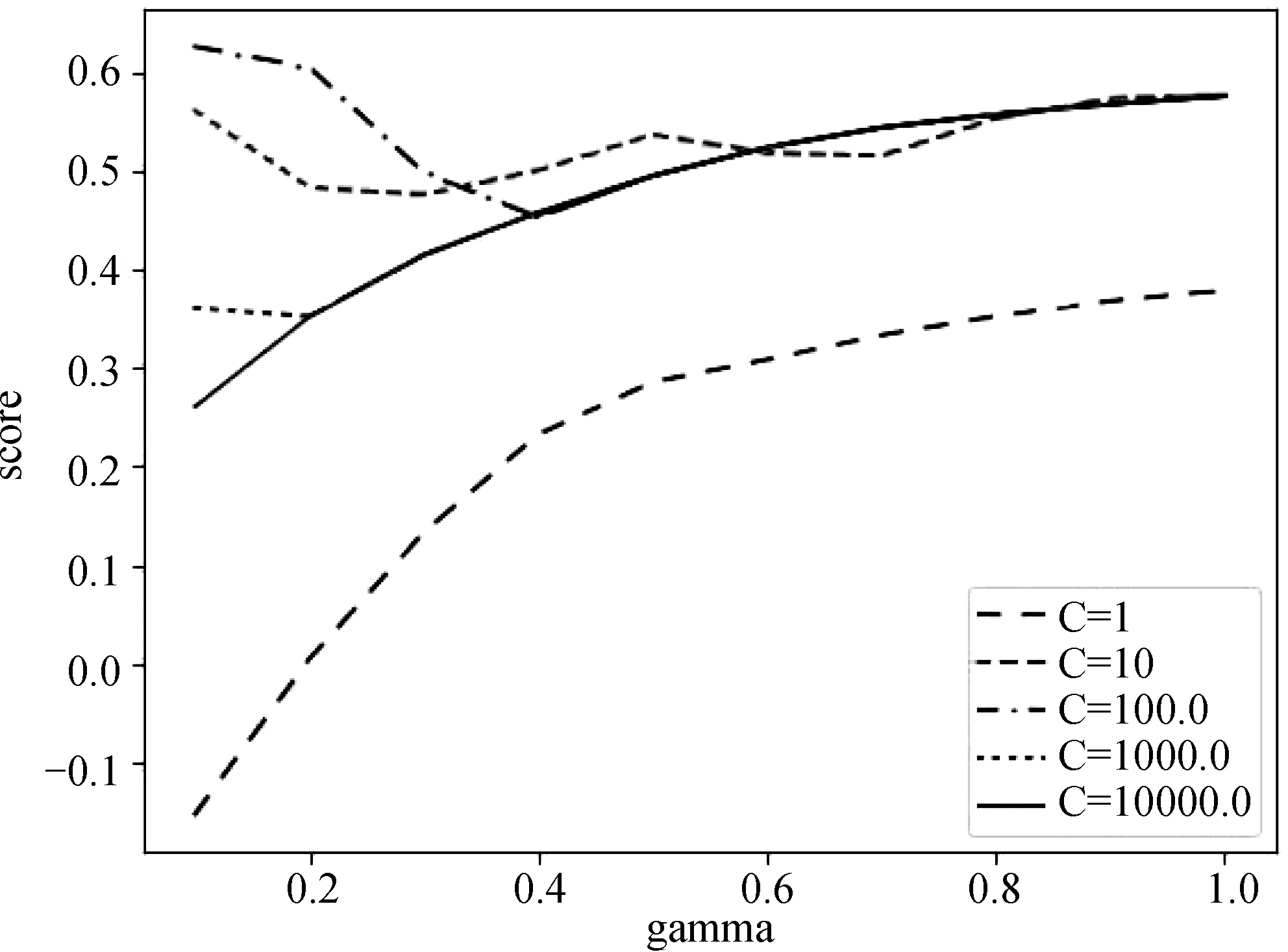
图2 径向基核函数模型评估图

3.应用结果与分析

将主成分分析后的数据作为样本数据，从中随机选取70%的数据作为训练集，建立预测模型，剩余30%作为测试集，检验模型的精确度和推广能力。SVR模型在训练集和测试集上的预测效果分别如图3与图4所示。

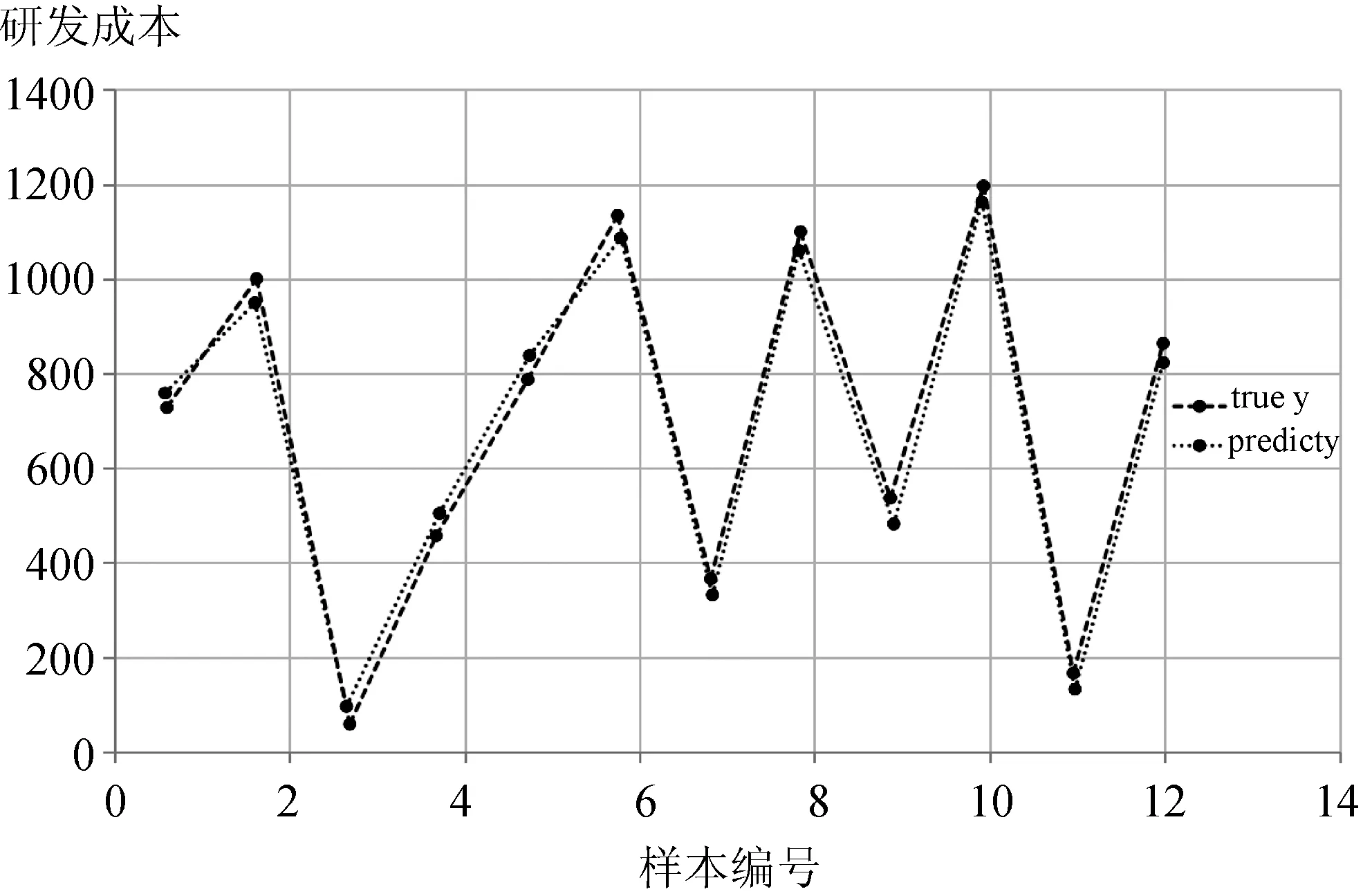
图3 SVR模型在训练集预测效果

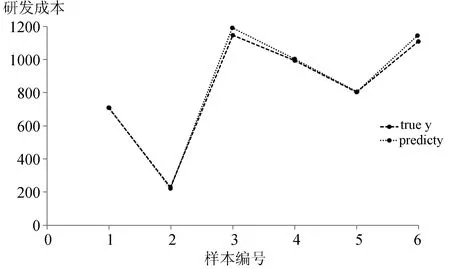
图4 SVR模型在测试集预测效果

由图3和图4可见，SVR模型在训练样本及测试样本上的拟合较好，真实值与预测值曲线基本重合，误差较小。其中，模型在训练集和测试集上的均方误差分别0.009 06和0.006 30。

为检验该模型的预测精确度，本文将PCA-SVR模型与贝叶斯岭回归模型(Bayesian Ridge)，梯度增强回归模型(Gradient Boosting Reg ressor)以及决策树化回归模型(DTR)进行对比，结果如图5所示。

由图5可知，PCA-SVR模型得到的高新技术企业研发成本预测值曲线与真实值曲线基本重合，拟合效果好，而其他模型的预测曲线与真实值之间在一定程度上有较大的差异。为分析各个模型预测效果与真实值之间的偏差程度，本文分析了前文介绍的4个指标(公式(6)～(9))，结果如表7所示。

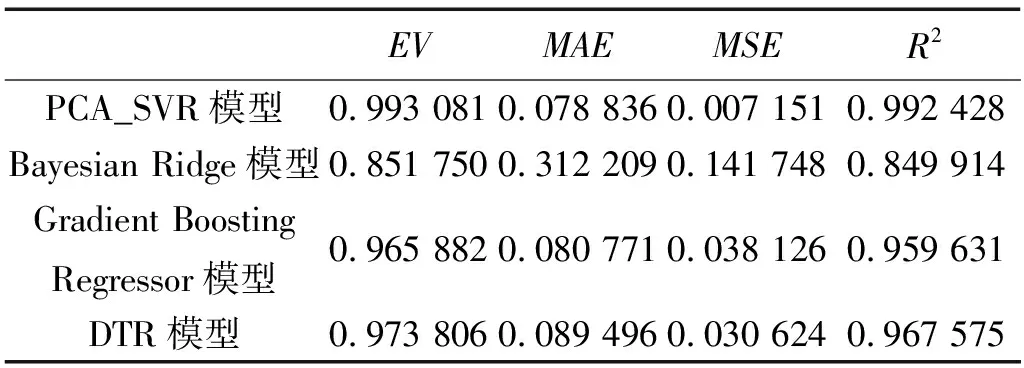
表7 指标对比

图5 各个模型的对比

根据表7数据，PCA-SVR模型的EV、R2值在4个模型中都是最大的且接近于1，MAE、MSE的值在4个模型中是最小的，进一步证明了PCA-SVR模型在高新技术企业研发成本预测中的有效性、精准性。此模型能够为高新技术企业研发成本预测提供中长期的技术支持。

综上，在考虑了高新技术企业的特性与研发成本的影响因素的基础上，PCA-SVR模型能够对高新技术企业研发成本进行准确预测。因此，本文根据相关数据，运用PCA-SVR模型对样本A公司2019～2022年研发成本(万元)进行预测，结果表明：2019年至2022年，研发成本分别为1 200万元、1 254万元、1 278万元和1 309万元。从预测结果可以看出，2019年至2022年A企业的总体研发成本逐年增加，但增加幅度呈现先增后减趋势。这表现出一定的波动性，符合研发活动的特征。

通过以上案例分析，证明了PCA-SVR模型在实际应用上能够对研发成本实现准确预测。此外，对于以A公司为代表的高新技术企业，PCA-SVR模型不仅能够为其预测未来研发成本的走势，并且能够帮助企业筛选影响研发成本的关键因素，为管理者制定未来的研发预算决策提供重要依据，以便合理、有效地利用有限资源，进而为企业带来更大的利润空间。

五、结论与管理建议

研发活动是高新技术企业发展的基础，更是创新的源泉。因此，对研发活动支出的准确预测，能够提升企业研发活动的成功率，从而降低研发风险。同时，也能为高新技术企业的决策者提供有效的决策依据与技术支持，进而为企业实现经济效益最大化制定科学、正确的管理方案。

本文针对高新技术企业研发活动中的成本规划问题和现有成本预测方法存在的不足，分析确定了高新技术企业研发成本主要影响因素，针对要素复杂、随机性强、预测难度大的情况，设计并使用主成分分析与支持向量机相结合，构建了高新技术企业研发成本PCA-SVR预测模型。预测过程中考虑了团队科研技术水平、创新能力、市场占有率、竞争者数量、市场规模、经营现金流量与通货膨胀率等变量之间的内在关系，通过模型优化选择最适合样本数据结构的预测模型。应用分析结果表明，预测值与真实值拟合效果良好，准确验证了本文所构建模型的适用性和精确性，为高新技术企业研发成本预测在理论分析和实际应用上提供有益的参考和借鉴。

此外，由于收集的数据精准度与范围有限以及模型自身的局限性，预测误差会在一定区间内波动，并且在实际应用方面还不成熟。因此，对于高新技术企业研发成本的预测还需要更深入的研究与更全面的考量。

鉴于本文的预测和分析结果，为高新技术企业研发成本预测提出了如下建议：第一，企业要注重研发能力在成本预测中的关键作用。本文分析的研发能力标志着企业的核心竞争力，体现在研发团队的创新成果上，贯穿于企业生产的创新实践中。构建适应团队发展的创新人才培育体系，形成产学协同创新机制，将逐渐成为高新技术企业提升研发能力的有效途径与方法。第二，在生命周期的不同阶段实施差异化研发投入政策。高新技术企业研发投入具有较强的不确定性，并呈现波动性特征，不同生命周期阶段投入成本的差异性很大，要紧密结合市场占有率、竞争者数量等市场特征，准确预测研发成本，有效规避投入风险，为企业精准施策提供数据支撑。