一种导模共振窄带宽的平顶滤波器设计
王承浩,王 晨,王 琦,成丁尔,张大伟
(上海理工大学 光电信息与计算机工程学院,上海 200093)
引 言
在一特定入射条件时,入射光波与亚波长光栅之间发生的相互耦合作用会使传播波的光场能量重新分配,从而使光栅在共振波长处具有高的反射或透射特性,该现象即为导模共振效应[1-3]。基于光栅结构的导模共振器件因为其相对简单的制造工艺和设计原理被广泛应用在光学滤波器[4]、偏振片[5]、光开关[6]以及光调制器[7]中,还可应用于提高自发辐射的提取效率以及激光的辐射模态控制等领域[8-10]。
当两个导模共振(GMR)相互作用时,共振特性可以调谐。两个GMR元素之间的相互作用有两种发生途径:一种是平板波导的直接倏逝耦合,另一种是通过自由空间传播的间接耦合[11]。根据这些耦合机制的相对强度,我们会观察到不同的共振特性。Arbabi等[12]提出了一种双宽带GMR反射器,用其实现可调谐的窄带法布里-珀罗(F-P)传输滤波器,但是其缺少了GMR的传输模式。Ko等[13]将F-P共振腔和GMR结合以产生平顶型滤波的效果,并且利用多层级联结构,使带宽变宽。通过调谐各级联结构之间的距离,可以达到抑制边带的效果。但是其带宽较窄,大约只有0.5 nm。Yamada等[14]提出了一种窄带平顶滤波器,运用夹在两个波导中间的单一光栅层,实现了高效的平顶光谱。由于这种结果是通过同时诱导几乎简并的共振模态来获得的,所以共振分别控制了平顶光谱的宽度。这说明带宽可以在亚纳米到几纳米之间调整。
在光通信技术中,由于信道光在传输过程中会产生漂移,通常情况下都要求滤波器具有一定的调谐功能或带通平顶特性。然而,目前的结构普遍存在通带过窄、边带过高或者难以调谐的问题。为了设计一款带通效果较好且结构简单的平顶型滤波器,本文提出一种双层波导结构,将通带宽度提高到2 nm,半高全宽提高到6 nm,且具有良好的边带抑制效果,同时由于其结构简单,因此易于制作并与其他器件集成使用。
1 平顶滤波器设计原理
1.1 滤波器结构
由于单层波导结构只会产生一个导模共振峰值,难以产生好的平顶共振效果,因此我们选用能产生两个共振峰的双层波导结构,以达到平顶滤波的目的。图1为本文提出的亚波长双层波导结构平面图(XZ平面),该结构是由光栅层、波导层以及衬底层组成的单层光栅对称耦合而来。根据 Magnusson等[15-16]的研究,平面介质波导光栅的导模共振特性以及谐振的线宽可以通过调整光栅参数和边界处折射率差来控制。本文采用的单层光栅的结构参数为:光栅层及波导层材料为晶体硅(Si);光栅周期Λ为740 nm;光栅脊宽度ω为380 nm;光栅厚度dg为250 nm;波导层厚度dw为200 nm;外部环境为空气,折射率nc=1;衬底材料为SiO2,其厚度ds为350 nm。
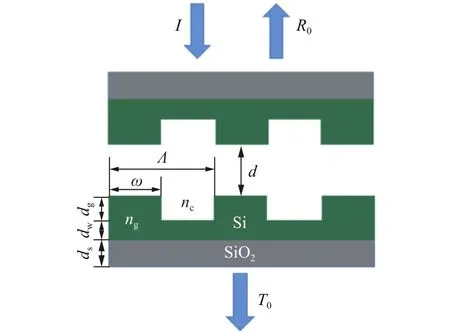
图1 双层波导结构模型Fig.1 Double-layer waveguide structure model
该实验利用时域有限差分(FDTD)法对结构进行分析,采用FDTD Solutions软件对该双层波导结构进行仿真,选取一个周期作为分析对象,入射光以TE模式垂直照射到光栅表面,最终对采集到的透射光进行理论分析。
1.2 设计原理
图2为由衬底层、波导层以及光栅层组成的经典导模共振光栅一维结构。其中ns为衬底层折射率,nw为波导层折射率,nh、nc分别为光栅层高低折射率,dg为光栅层厚度,dw为波导层厚度,Λ为光栅周期,ω为光栅脊宽度,因此光栅的占空比为f=ω/Λ 。
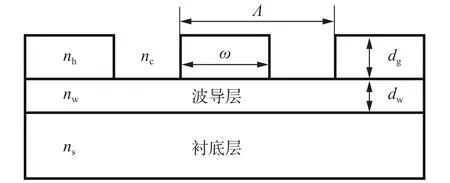
图2 经典导模共振光栅Fig.2 Classic guided-mode resonance grating
根据等效介质理论,可以将亚波长光栅层视为均匀介质波导[17]。当某一级次的衍射波正好与波导所支持的某个模式相位匹配时,对应的入射光能量将耦合到这一模式当中,第j级衍射波将引起共振效应,即

式中:k0=2π/λ;θ为入射角度。为了保证导模共振发生,波导层的折射率nw应大于入射空间折射率nc以及衬底层折射率ns。为了得到较好的滤波特性,应保证光栅层具有较高的空间频率,从而使衍射波只有零级透射波和反射波,其他高级次衍射波转化为倏逝波。
本文通过单层GMR产生透射光谱共振峰,再将其对称耦合以产生另一个可调谐的共振波长,最后调整光栅间距,使两个峰值分别落在对方半波宽处以达到平顶的效果。这样的结构可以理解为是一种夹在两个反射器之间的类F-P腔。我们可以通过调节光栅调制强度和占空比获得更大的共振线宽,以达到更好的平顶滤波效果。
1.3 结构特性分析
采用FDTD Solutions软件进行计算,得到本结构的透射光谱。首先分析单层光栅的传输特性,图3是单个导模共振光栅衍射效率光谱,当入射光为TE偏振时,单层光栅在λ=1 131 nm处产生了共振峰,透射率超过88%。
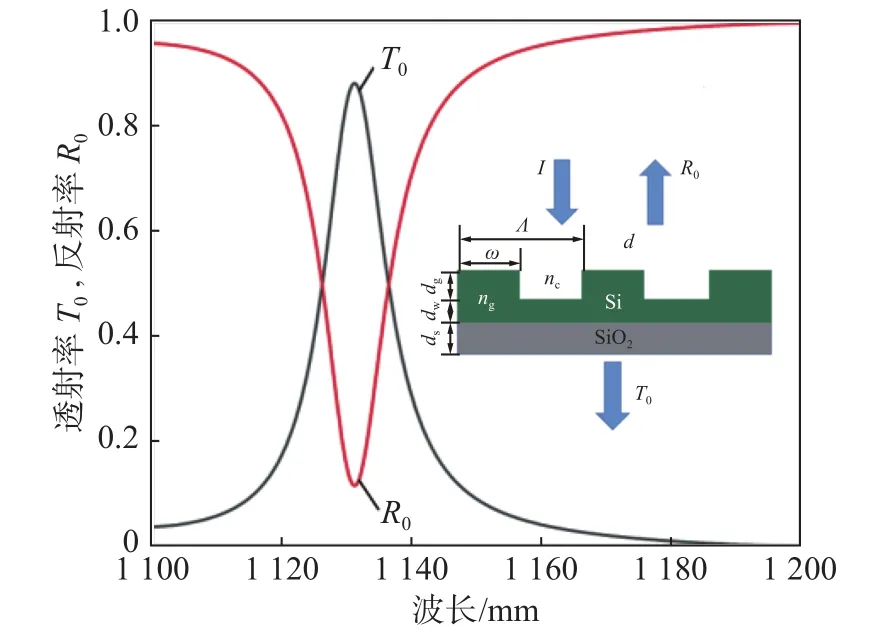
图3 单个导模共振光栅衍射效率光谱Fig.3 Diffraction efficiency spectrum of single guided-mode resonance grating
图4为单层光栅和双层光栅的电场分布,由(a)可以看出,共振发生在光栅层与波导层的交界处,共振强度较强,是典型的导模共振效应。这样的单层光栅有时被称为零对比度光栅(zerocontrast grating,ZCG)[18]。本文通过严格耦合波分析方法(RCWA)[19]对其进行了优化,得到了较好的效果。
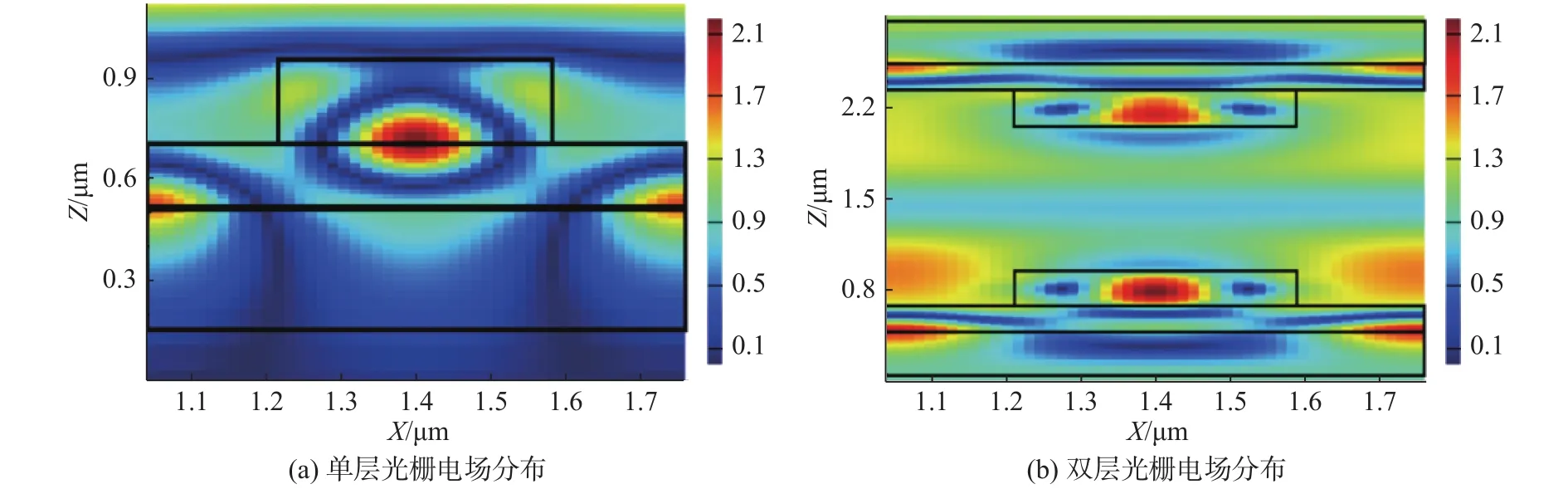
图4 电场分布Fig.4 Electric field distribution
我们在单层光栅上方对称放置一个相同的光栅使其变为双层光栅。图5是双层光栅对称结构与单层光栅透射率的对比图。由图可以看出,双层GMR相比于单层GMR拥有更高的透射率以及更陡的斜率,同时拥有更窄的半高全宽(FWHM)。由于类F-P腔峰值的结合,在透射谱线上产生了平坦的峰,同时GMR峰值并没有出现明显的变化。经过测量,该结构的平顶滤波范围为2 nm。图4(b)是双层GMR的电场强度分布,由图可知,双层GMR发生共振的位置处在上下光栅层中。
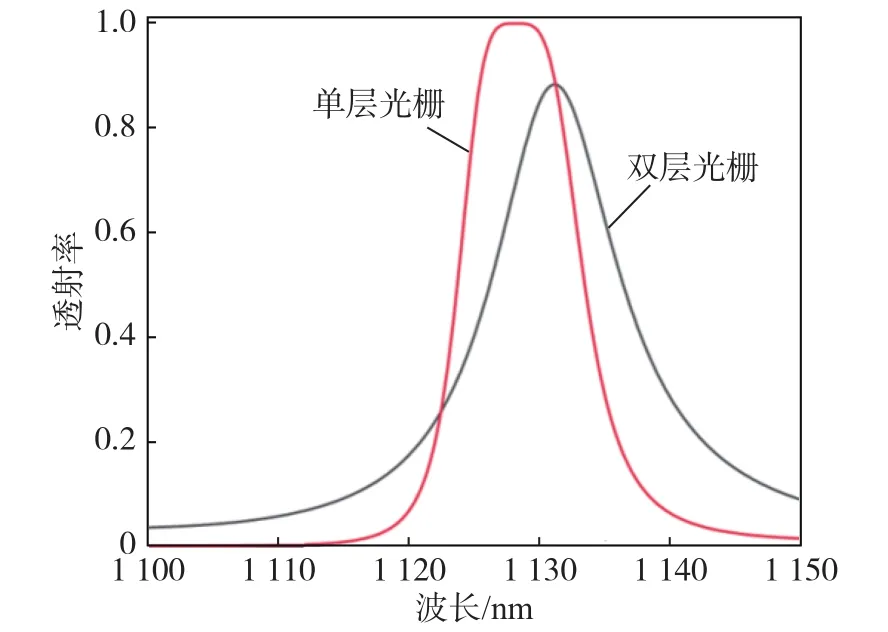
图5 TE 波正入射情况下单,双层光栅的零阶透射率Fig.5 Zero-order transmittance of single and double-layer gratings under TE polarization at normal incidence
对于单光栅,需要使用亚波长结构以获得高反射率,此时光栅周期应满足
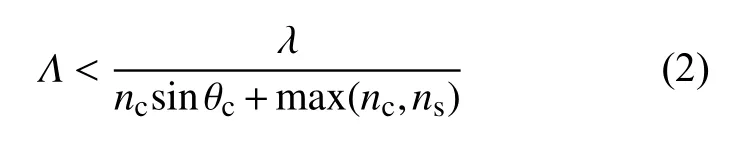
式中:λ为自由空间波长;θc为入射角度;ns为衬底折射率。式(2)显示了光栅周期与入射波长之间的关系,因此大致的光栅周期可以被计算出来。
对于由高反射光栅组成的双层结构,可以近似地看作类F-P腔[20]。设δ为相移,则其可以定义为
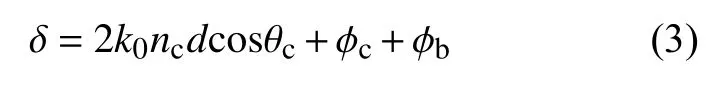
式中:k0=2 π /λ; φc为上层光栅和夹层空气临界面处的反射相移; φb为下层光栅和夹层空气临界面处的反射相移。由于光栅结构是对称的,所以此处 φc= φb。
设ttot与rtot分别表示透射率与反射率,随着δ趋向于 2mπ(m=0,1,2,···),ttot趋向于1而rtot趋向于0,因此类F-P腔的共振波长λres可以被写作
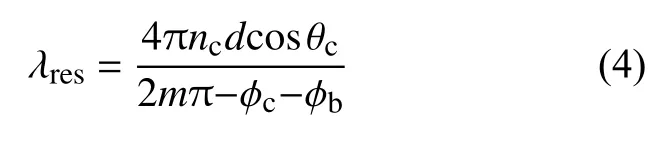
通过式(4)可以看出,随着板间距离d的变化,类F-P腔的共振峰值也会相应变化 。
图6是透射率与双光栅板间距离d的关系曲线,随着d的减小,类F-P腔产生的共振峰发生了蓝移,这与理论计算的结果相吻合。

图6 d 与透射率的关系Fig.6 Relation between transmittance and d
为了明确双层结构的可调谐性,对不同周期的光栅进行了研究。图7(a)为不同周期条件下,单层结构共振峰值的偏移情况。由式(4)可知,保持光栅结构的占空比不变,单层GMR的共振峰值位置是随着周期增大而增大,因此为使平顶效果依然存在,类F-P腔产生的峰值也应随之移动。图7(b)为双层光栅的共振峰值的偏移情况,由此可见,增大光栅板间距离d,可使类F-P腔共振峰向长波方向偏移。图7(c)为共振峰值与不同Λ、d的函数模型。
从图7可以看出,随着波长以及板间距离的增加,平顶峰的位置也在增加,这为该结构在不同波长要求下工作提供了理论依据。例如可以在不同的通信波段之间进行调节以实现更加广泛的应用。
本文提出的双层光栅结构能够产生2 nm宽的平顶滤波效果,同时半高全宽达到了6 nm。相比于普通多层膜产生的法布里-珀罗腔型平顶滤波器,本文结构更简单,带宽更宽并且具有可调谐的特性。根据式(4),F-P腔的共振峰位置也和腔内填充物质的折射率有关。填充不同的物质会使共振峰位置发生偏移,因此该结构在传感领域也具有潜在的应用前景。
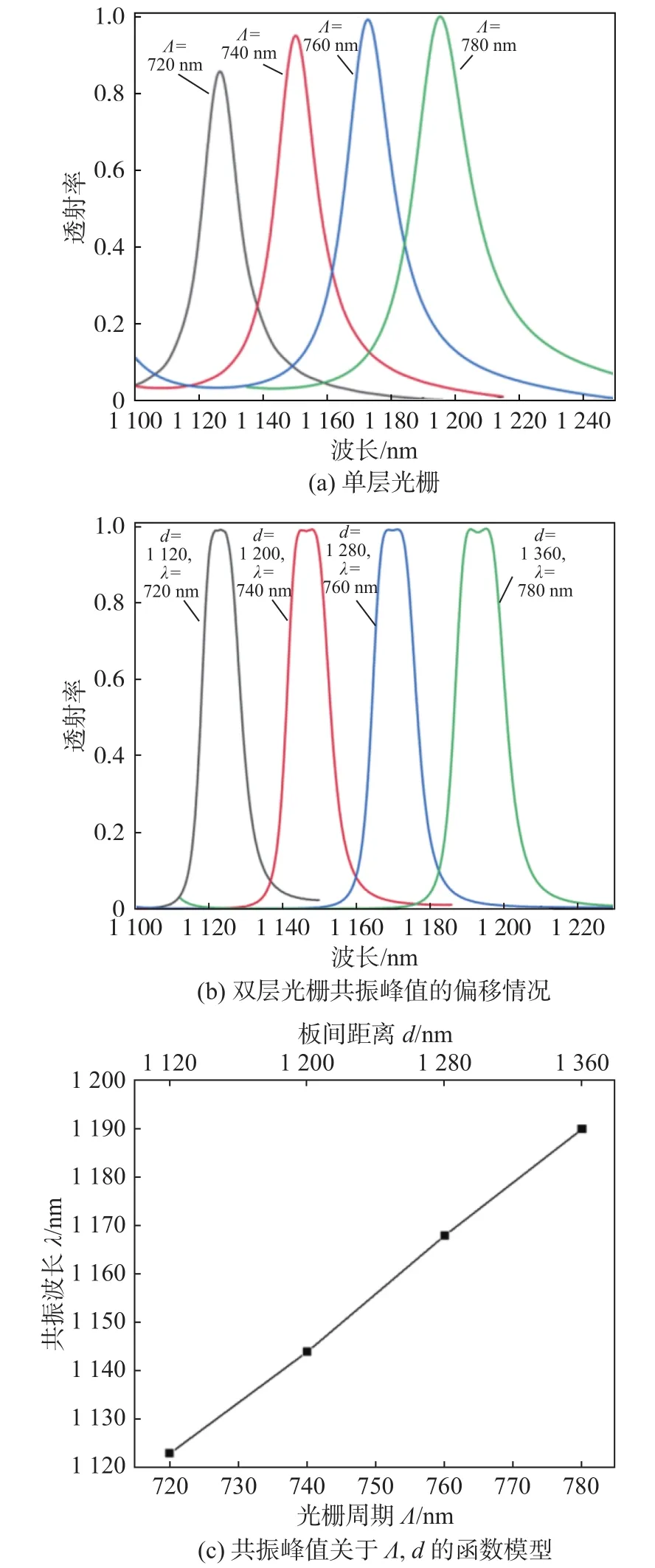
图7 不同 Λ,d 条件下,共振峰值的偏移情况及函数模型Fig.7 resonance peak shift and Resonance peak function model Under different Λ, d conditions
2 结 论
本文依据严格耦合波理论和等效介质的数值计算方法,通过FDTD软件的仿真优化,设计了一种亚波长介质光栅。该结构可以产生导模共振,将其与类法布里-珀罗谐振腔结合,可以获得较好的平顶滤波效果。平顶宽度达到2 nm,半高全宽达到6 nm,且峰值位置可以调谐。在现代光通信领域中,该结构可以有效应对信道光漂移带来的问题,同时可调谐的特性还可以应对不同情况下的通信要求。有别于传统的多层膜结构,我们实现的平顶型滤波器结构更加紧凑,带宽更宽,对信道光的漂移具有更大的容忍度。

