黄淮地区辐射模型适用性评价及参数优化
王晓东 曹雯 伍琼 岳伟 段春锋
(1 安徽省农业气象中心/安徽省农业生态大数据工程实验室,合肥 230031;2 安徽省气候中心,合肥 230031)
引 言
地表净辐射是地表通过短波、长波辐射过程得到的净能量,它是气候变化乃至全球变化的重要驱动力,它作为热源,供地表及贴地大气层的增温或降温及蒸发、蒸腾的耗热,是研究地表能量转换、流域蒸散、水分循环的重要因素,同时也是构建各类生态模式的重要参数之一[1-5]。其资料获取途径主要有通过净辐射仪直接测量和通过辐射平衡方程中其它常规观测要素的计算以及利用遥感资料推算而间接获得等[6-8]。目前我国气象系统仅有53个地表净辐射观测台站,均建于1993年以后,由于净辐射站点少、分布不均且资料序列短,远远满足不了农业、环境和气象等领域中科研和业务的需求,而通过遥感方法推算净辐射则首先需要获取大气影响参数,相对较为复杂,因此通过辐射平衡方程研究地表净辐射的推算方法显得十分重要[9-12]。
太阳总辐射和地面有效辐射是构成地表净辐射的两大主要分量[13-14]。其中应用较为广泛的太阳总辐射估算模型主要有左大康公式、翁笃鸣公式、童宏良公式、FAO56公式、YIN 公式和YANG公式等[15];应用较为广泛的地面有效辐射估算模型主要有邓根云法、彭曼法、布朗特法和别尔良德法等[16],但各种估算方法在不同区域的适用效果存在较大差异[17-18]。其中联合国粮食及农业组织(FAO)在其发布的文件FAO56 中推荐的辐射参数在计算辐射时应用最为广泛,但由于气候和地理等条件的差异,往往不同地区适宜的取值参数有所差异,国内相关学者也开展了大量辐射模型的本地化研究,如周秉荣等[19]、吴文玉等[20]、何利德等[21]分别基于各地区的辐射观测资料建立了青海、安徽和杭州等地太阳辐射估算模型参数,曾燕等[22]、李韧等[23]、刘绍民等[24]利用地面辐射资料分别计算分析了黄河流域、青藏高原和新疆等地区的地面有效辐射的参数化方案。
黄淮地区主要由黄河、淮河下游泥沙冲积而成,除西部和山东部分丘陵外,主要以平原为主,地势平坦,是我国重要的粮食主产区之一,参考作物蒸散量的计算十分重要,太阳辐射尤其是净辐射资源直接影响到小麦和玉米等主要农作物的生产效率以及该区农业生产的高产稳产[25],因此利用实测数据对辐射估算方法进行适用性评价并建立本地区最优的辐射估算方法显得尤为重要。本文拟利用黄淮地区主要站点的气象和辐射观测资料,评价太阳总辐射和地面有效辐射常用估算模型的本地区适用性,同时通过辐射参数的调整,建立本地区辐射的最优化估算模型,从而提升地表净辐射的计算精度,以期为本地区辐射资源评价、作物生产潜力评估等提供更加准确和有效的数据支撑。
1 资料与方法
1.1 资料来源
收集由国家气象中心气象资料室整编的1961—2015年黄淮地区8个辐射台站(表1)太阳辐射资料和逐日最高(最低)气温、平均气温、实际水汽压、相对湿度和日照时数等常规气象资料,并剔除由仪器故障等原因造成的异常数据和错误数据,进行适当的插补和筛选后,开展了质量控制,其中太阳辐射剔除大于天文辐射,小于0.03倍天文辐射的样本。

表1 黄淮地区辐射资料观测台站信息表Table 1 Information of radiation site in Huanghuai Region
1.2 计算方法
1.2.1 辐射平衡方程
根据辐射平衡方程地表净辐射可通过太阳总辐射和地面有效辐射计算获得,净辐射的计算公式如下:
Rn=Rns-Rnl,
(1)
Rns=(1-α)Rs。
(2)
式中:Rn为净辐射;Rs为太阳总辐射;Rns为净短波辐射;Rnl为净长波辐射(地面有效辐射);辐射单位均为MJ·m-2·d-1;α为地表反射率。
1.2.2 太阳总辐射估算模型
太阳总辐射是地球表面某一观测点水平面上接收太阳的直射辐射与太阳散射辐射的总和,因不同区域气候和地理条件不同,而略有差异。已研究得到了针对不同区域的太阳总辐射各类经验公式,为评估各类太阳总辐射估算模型在黄淮地区的适用性,本文评估了其中6种常用太阳总辐射估算模型(表2),其中:R0为天文辐射,即到达大气上界的太阳辐射,可由太阳常数、日地距离和太阳赤纬等要素计算获得;Ra为晴空辐射为地面晴空状态下的太阳辐射,可由天文辐射通过海拔等要素订正获得[26];n为实际日照时数;N为可能日照时数。

表3 常用地面有效辐射估算模型Table 3 Common estimation model of surface effective radiation
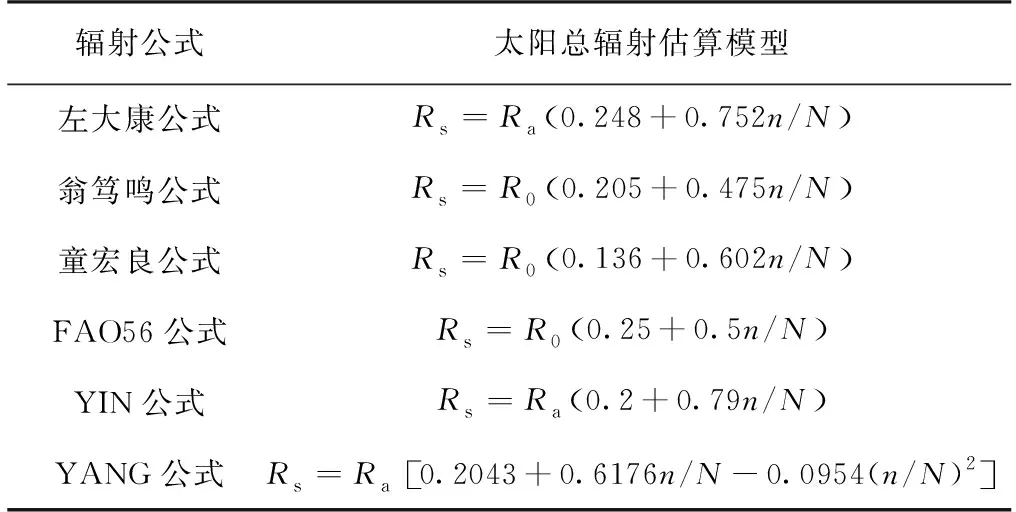
表2 常用太阳总辐射估算模型Table 2 Common estimation model of global solar radiation
1.2.3 地面有效辐射模型
地面有效辐射为地面辐射和地面所吸收的大气逆辐射之间的差值,与太阳辐射估算模型相似,地面有效辐射的估算也因不同区域气候和地理条件不同而存在一定的差异,许多学者借鉴有效辐射经验公式的基本形式并利用不同地区的观测资料,获得了计算有效辐射的多种参数化方案,本文研究评估了其中6种常用地面有效辐射估算模型(表3),其中σ为斯蒂芬—玻尔兹曼常数,其值为5.67×10-8W·K-4·m-2;Tmax和Tmin分别为最高气温和最低气温(单位:K);ea为实际水汽压(单位:kPa)。
1.2.4 误差分析
为评价辐射模型各种参数化方案的估算精度和稳定性,分析辐射估算值与实测值之间的相对误差(Relative Error, RE)、相对误差绝对值(value of Absolute Relative Error, ARE)和均方根误差(Root Mean Squared Error, RMSE),其中Ei和Ri分别代表估算值和实测值。
(3)
(4)
(5)
2 结果分析
2.1 辐射估算模型在黄淮地区的适用性
利用6种太阳辐射估算模型和实测辐射值计算出黄淮地区逐日太阳辐射估算误差(表4)。各估算模型的估算精度存在较大差距,误差分析显示童宏良公式的估算误差最小,其相对误差(RE)和相对误差绝对值(ARE)分别为6.46%和21.72%,而FAO56公式的估算误差最大,其RE和ARE分别达到了31.96%和35.37%,另外除YIN公式的估算值相较于实测值整体偏小(-7.69%)外,其余5个公式的估计值均偏大;RMSE值显示翁笃鸣公式、童宏良公式和YIN公式的均在2.5 MJ·m-2·d-1左右,总体估算稳定性好于其余3个估算模型。

表4 6种常用太阳总辐射估算模型的误差对比Table 4 Error comparison in six common estimation model ofglobal solar radiation

图1 6种太阳总辐射模型估算误差的年内分布:(a)相对误差绝对值; (b)均方根误差Fig.1 Annual distribution in six model estimation error of global solar radiation:(a)ARE; (b)RMSE
图1是6种太阳总辐射模型的估算误差年变化。从相对误差绝对值(ARE)可以看出,6种估算模型的估算偏差在年内普遍呈双谷型分布,其中春季和秋季偏差总体较小,而夏季和冬季的估算偏差相对较大;从各模型的估算精度来看,估算精度最大的是童宏良公式,各月的ARE值为18%~25%,其次是YIN公式,各月的ARE值为19%~27%,估算偏差相对较小,而估算偏离程度最大的是FAO56公式,各月的ARE值达到了29%~41%,估算精度最低。从逐月RMSE可以看出,6种估算模型在年内普遍呈单峰型分布,冬季估算误差值发生波动的幅度相对较小,其次春、秋季,而夏季估算误差值发生波动的幅度相对最大,从各模型的估算稳定性程度来看,翁笃鸣公式的各月RMSE值最小,其值为1.5~3.3 MJ·m-2·d-1,其次是童宏良公式和YIN公式,其值为1.6~3.5 MJ·m-2·d-1,相较其余3个估算模型,误差估算稳定性较高,说明在年内具有较稳定的适用性;而误差估算稳定性最差的是YANG公式,各月的RMSE值达到了2.0~5.1 MJ·m-2·d-1。
黄淮地区8个辐射台站中仅郑州站有实测有效辐射资料,因此以郑州站为代表,利用6种有效辐射估算模型和实测有效辐射值计算逐日有效辐射估算误差(表5)。各估算模型的精度存在较大的差异,误差分析显示相对误差(RE)均为负值,表明各估算模型整体上都不同程度低估了有效辐射。其中由于别尔良德法、FAO24和FAO56-PM基本上所有的估算值均偏小,因此总体低估程度较大;而布朗特法、Penman法和邓根云法均存在估算值偏大的数值,由于正、负偏差的抵消作用,低估程度相对较小。其中邓根云公式的估算误差最小,其RE和ARE分别为-6.23%和24.19%,而FAO56-PM公式的估算误差最大,其RE和ARE分别达到了-60.43%和60.49%,邓根云公式的RMSE值为1.633 MJ·m-2·d-1,总体估算稳定性明显好于其余5个估算模型(RMSE为2.0~3.1)。
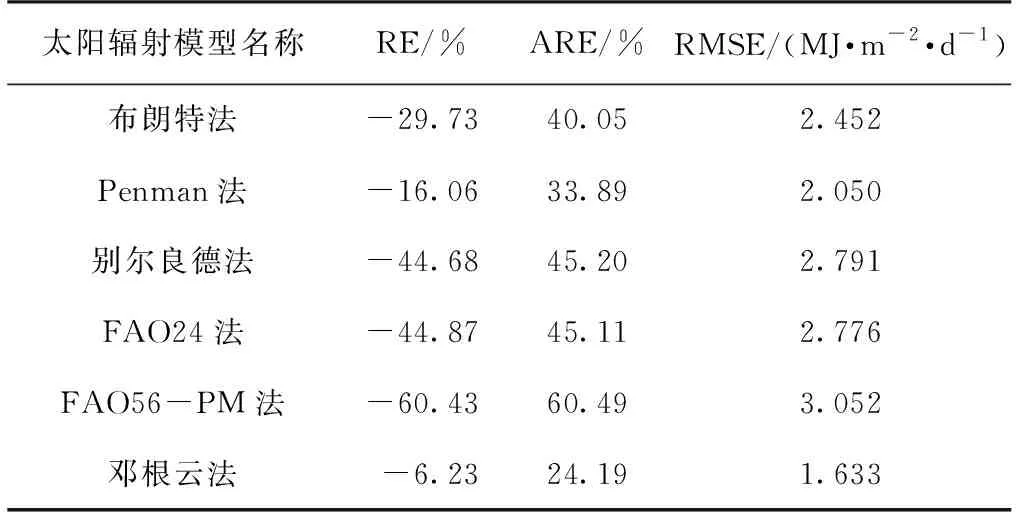
表5 6种常用地面有效辐射估算模型的误差对比Table 5 Error comparison in six common estimation modelof surface effective radiation
图2是6种地面有效辐射模型的估算误差在年变化。从相对误差绝对值(ARE)可以看出,6种估算模型的估算偏差在年内普遍呈单峰型分布,峰值大多出现在夏季,春秋季偏差总体较小;从各模型的估算精度来看,估算精度最大的是邓根云公式,各月的ARE值为20%~26%,各月的误差均小于其他5个估算模型,估算偏差相对较小,而估算偏离程度最大的是FAO56公式,各月的ARE值达到了56%~68%,估算精度最低。从逐月RMSE可以看出,6种估算模型在年内普遍呈单峰型分布,夏季估算误差值发生波动的幅度相对最大,从各模型的估算稳定性程度来看,邓根云公式的大部分月份RMSE值最小,其值为1~2 MJ·m-2·d-1,仅3月和4月略高于Penman法,相较其余5个估算模型,误差估算稳定性较高,说明在年内具有较稳定的适用性;而误差估算稳定性最差的是FAO56公式,各月的RMSE值达到了2.0~4.0 MJ·m-2·d-1。

图2 6种有效辐射模型估算误差的年内分布:(a)相对误差绝对值; (b)均方根误差Fig.2 Annual distribution in six model estimation error of surface effective radiation: (a)ARE;(b)RMSE
通过太阳总辐射和有效辐射估算模型的估算精度和稳定性分析,总体上童宏良公式在估算太阳总辐射的精度和稳定性最好,邓根云公式在估算地面有效辐射的精度和稳定性最好,而FAO56通用公式在估算太阳总辐射和地面有效辐射时的估算误差最大,说明FAO56通用公式对黄淮地区辐射估算适用性较差,综上所述黄淮地区估算太阳总辐射和地面有效辐射适用性最好的分别为童宏良公式和邓根云公式。
2.2 黄淮地区辐射模型最优参数化方案
基于黄淮地区8个辐射台站的太阳辐射资料和日照时数等气象资料,以日照百分率为自变量,太阳总辐射与天文辐射的比值为因变量,采用多元回归分析方法拟合出FAO56推荐的太阳辐射估算模型中的经验系数a、b值,其中采用交叉验证的方法,将奇数年的样本用于建立参数化方案,偶数年的样本用于效果检验,得到太阳总辐射本地化修正模型:
Rs=R0(0.172+0.535n/N)。
(6)
修正模型的检验误差(表6)显示相对误差(RE)、相对误差绝对值(ARE)和均方根误差(RMSE)分别为5.41%、16.28%和1.73 MJ·m-2·d-1,估算精度高于童宏良公式等常用太阳辐射估算模型;年内的误差变化情况(图3)来看,修正后模型也明显好于适用性最好的童宏良公式。

表6 太阳总辐射修正模型的估算误差Table 6 Estimation error in correction model of global solar radiation
同理基于黄淮地区实测的有效辐射资料,采用步长加速法,对有效辐射模型基本形式(公式略)中的参数a(取值0~1,步长0.01),参数b(取值0~1,步长0.001),参数c(取值0~1,步长0.01)进行迭代取值,利用多元回归法计算获取不同的a、b、c参数组合和相应的有效辐射值,采用交叉验证的方法同太阳辐射修正模型,最终以计算的有效辐射值和实测值之间ARE最小,确定参数取值,得到有效辐射本地化修正模型(公式8)。
修正模型的检验误差(表略)显示RE、ARE和SE分别为2.43%、23.19%和1.404 MJ·m-2·d-1,估算精度高于邓根云公式等常用有效辐射估算模型;年内的误差变化情况(图4)来看,上半年修正后模型明显好于适用性最好的邓根云公式,下半年修正后模型的估算精度与邓根云公式相似,总体来说修

(7)

图3 童宏良和修正模型估算误差的年内分布:(a)相对误差绝对值; (b)均方根误差Fig.3 Annual distribution of estimation error in TONG hongliang and correction model:(a)ARE;(b)RMSE
(8)
正后模型好于适用性最好的邓根云公式。
基于公式(6)和公式(8)得到黄淮地区地表净辐射本地化修正模型,即公式(9);其中:反照率α取0.23。利用模型计算黄淮地区3个辐射台站(郑州、福山和济南)的净辐射,对比站点实测的净辐射值,评估其估算误差进行,误差分析显示3个站点逐日RE和ARE值分别为5.13%和20.48%,RMSE值为1.511 MJ·m-2·d-1,总体估算效果较好。
(9)
3 结论
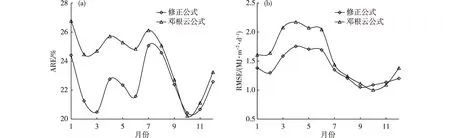
图4 邓根云和修正模型估算误差的年内分布:(a)相对误差绝对值; (b)均方根误差Fig.4 Annual distribution of estimation error in DENG genyun and correction model: (a)ARE;(b)RMSE
虽然辐射估算的经验性模型不少,也有许多推荐的通用性模型,但受地域和辐射观测数据的影响,模型的估算精度有较大的差别,为提升地表净辐射的计算精度,本文基于黄淮地区主要站点的气象和辐射观测资料,评估了常用太阳总辐射和地面有效辐射估算模型在黄淮地区适用性;同时通过迭代和误差分析等方法对辐射参数进行了优化调整,建立了适合本地区最优的辐射估算模型。主要结论如下:
(1)分别分析6种太阳辐射估算模型和有效辐射估算模型的总体误差和年内误差,表明童宏良公式在估算太阳总辐射时的误差最小,邓根云公式在估算地面有效辐射时的估算误差最小,相比其余的辐射估算模型,童宏良公式和邓根云公式在黄淮地区适用性最好;而FAO56通用公式对黄淮地区辐射估算适用性均较差,为不同区域辐射参数的本地化修正提出了要求。
(2)基于黄淮地区辐射站的辐射资料和日照时数等气象资料,采用多元回归分析和迭代等方法拟合出推荐的太阳辐射和有效辐射估算模型中的经验系数,其中通过交叉验证的方法,建立了本地化最优参数方案。太阳辐射本地化修正模型的估算精度高于童宏良公式等常用太阳辐射估算模型;有效辐射本地化修正模型的估算精度高于邓根云公式等常用有效辐射估算模型;因此本地化辐射修正模型可用于黄淮地区地表净辐射的估算。
虽然前人利用单站开展过当地相关辐射估算研究,但本文充分利用黄淮地区8个辐射观测台站的辐射数据资料,数据的代表性更好。另外,本地化辐射修正模型估算精度虽然明显好于其余几种常规的辐射估算模型,但估算ARE值仍有15%~25%,今后的工作中需在参数优化方面开展更加细致深入的工作,以便提高黄淮地区辐射估算精度。

