一种用于小模数多项式乘法快速数论变换的扩域方法*
殷彦昭, 乌力吉, 张向民, 徐 科, 杨 维
1. 北京信息科学与技术国家研究中心, 北京100084
2. 清华大学 微电子学研究所, 北京100084
3. 中兴通讯股份有限公司, 深圳518057
1 引言
在基于R-LWE[1]原理的格密码中, 多项式环乘法是最为关键的基础运算, 也是算法设计和实现时最需要进行优化的运算模块. 如果不进行优化, 则多项式乘法的复杂度为O(n2), 其中n 是多项式长度. 多项式乘法的高复杂度会严重拖慢密码算法的运行速度, 占用大量开销, 因此大多数基于R-LWE 的格密码算法使用快速数论变换来进行加速. 该方法利用多项式系数的有限域特性, 构造多项式时域和频域的相互变换关系, 将多项式乘法在时域的卷积变为频域上的点积, 并利用折半定理实现快速数论变换, 从而大幅提升多项式环乘法的运算速度. NTRU[2]、NewHope[3]等格密码算法都是采用该方法进行多项式乘法的快速实现.
使用快速数论变换进行多项式环乘法时, 多项式及其系数域的参数都需要满足一定条件, 这对格密码的设计带来了很大限制. 要进行快速数论变换, 多项式系数域的阶N 必须满足N −1 是多项式长度的倍数, 因此当模数小于多项式长度时(如LAC[4]算法等), 格密码算法就无法使用快速数论变换来进行加速了. 为了解决这一问题, 本文设计了一种多项式系数域的扩域方法, 使得系数域的阶数满足数论变换的条件, 实现快速数论变换来加速多项式乘法的实现.
本文主要贡献如下:
(1) 设计一种扩域构造方案, 使小模数多项式乘法满足数论变换的条件.
(2) 基于系数域扩域, 设计复合基快速变换方法实现快速数论变换.
(3) 对R-LWE 体系的格密码常用的小模数多项式环乘法应用扩域方法, 分析计算复杂度, 与未使用快速数论变换时的复杂度进行对比, 论证扩域法实现快速数论变换的有效性.
2 预备知识
2.1 符号定义

DIT 用于快速数论变换的时域抽取分治法
DIF 用于快速数论变换的频域抽取分治法
2.2 多项式环乘法
R-LWE 体系中的多项式乘法定义在多项式环上. 构造多项式环时, 首先需要为多项式的系数选择一个有限域, 一般是选择一个特征为q 的素域. 然后, 再选择模多项式f(x), 定义环上多项式乘法为g(x)×h(x)=g(x)h(x)mod f(x), 加法亦同, 加完之后需要模掉f(x). 由此, 由系数为Zq域元素的多项式和上述加法乘法组成多项式环, 记为Rq=Zq[x]/f(x).
现有的R-LWE 算法体系多采用f(x) = xn+1 作为多项式环的模多项式. 由于模去阶数为n 的多项式f(x) 后, 原多项式的最高次项为xn−1, 因此模xn+1 环上多项式长度最大为n. 设多项式系数的模数为q, 三个多项式g(x)、h(x)、r(x) 分别如式(1)、式(2)和式(3)所示, 则多项式环乘法r(x)=g(x)h(x)中各多项式系数的关系如式(4)所示, 称之为回环乘法结构. 该乘法结构是本文所研究的多项式乘法基础表达式.
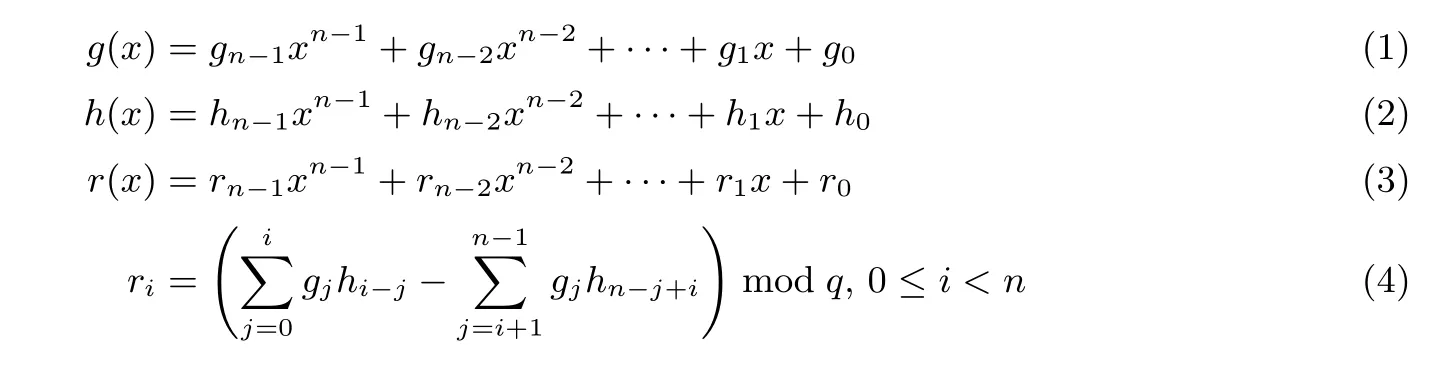
3 基2 快速数论变换实现多项式乘法
观察如式(4)所示的多项式乘法公式, 可以发现该表达式与数字信号处理中的循环卷积非常相似. 因此, 依据傅里叶变换中的“时域卷积对应频域相乘” 这一特性, 将多项式表示为类似于信号频谱的点值表示法, 将两个多项式的点值表示相乘之后再变换回原多项式, 可以进行乘法的快速实现. 将多项式变换为点值表示法的过程称为数论变换(NTT)[5], 其反过程称为逆数论变换(INTT). 在特殊的取值下, 利用类似快速傅里叶变换的折半定理, 便可将数论变换的复杂度降低至O(n log n), 其中n 为多项式长度.
3.1 多项式的点值表示法与数论变换
我们知道, n −1 次函数f(x) 上的n 个不同点可以唯一确定这个函数, 即唯一确定该函数的n 个系数. 同理, 长度为n 的多项式f(x) 也可以由n 组不同的点值对{xi,f(xi)} 唯一确定. 如果两个多项式用一组相同的自变量求出点值对, 则这两个多项式相乘的结果可以直接用点值对中自变量不变,因变量相乘来表示, 即f(x) ∗g(x) 的点值表示法为{xi,f(xi) ∗g(xi)}. 定义f(x) 在自变量序列为X = {xi|i = 0,1,2,··· ,n −1} 下的点值序列为F = {Fi|Fi= f(xi)}, 则使用点值表示法进行的多项式乘如算法1 所示.

算法1 使用点值法进行多项式乘Input: 多项式g(x),h(x), 自变量取值序列{xi}Output: r(x) = g(x)∗h(x)1 求g(x) 的点值表示法Gi = g(xi)2 求h(x) 的点值表示法Hi = h(xi)3 计算r(x) 的点值表示法Ri = Gi ∗Hi 4 由点值表示形式R = {R0,R1,··· ,Rn−2,Rn−1} 求解多项式r(x)
使用点值表示法进行多项式乘时, 自变量取值序列或集合的选择非常重要. 如果不能通过适当的自变量取值序列来快速实现多项式和点值表示法的互相转换, 使用点值表示法进行多项式乘就没有意义了.R-LWE 体系中多项式系数是有限域Zp中的元素, 因此利用有限域的性质可以寻找一个Zp上的生成元r 满足如下条件:
• r2n=1, 其中n 是多项式长度;
• 当0 ≤i,j <2n 且i ̸=j 时, ri̸=rj.

3.2 使用折半定理实现快速数论变换
虽然快速数论变换法能够提供对数量级的加速效果, 但并非所有多项式乘法都可以使用这种方法. 进行数论变换本身就对多项式及系数域的模数有一定要求, 而实现快速数论变换的要求则更为严苛. 首先,要生成数论变换的变换基{xi}, 就需要寻找生成元r, 而根据数论知识, 要满足r 的条件, 则有限域的模数q 必须满足q −1 是多项式长度n 的倍数. 又由于最佳效果的快速数论变换要求多项式长度为2 的幂次,据此可以得到快速数论变换对多项式长度和模数的要求:
• n=2k, k 为正整数
• q =n ∗C +1, C 为常数
• q 为素数同时满足这三个条件的参数取值组合很有限, 这也是R-LWE 体系算法的设计难点之一. 而像LAC 这样的小模数R-LWE 算法更是无法实现快速数论变换, 因为其模数小于多项式长度, 不可能满足q −1 是n的倍数这一条件. 因此, 我们尝试使用扩域方法来进行小模数多项式乘法的快速数论变换.
4 本文方法
小模数多项式乘法不能使用常规NTT 的原因是多项式系数域太小而无法构造NTT 变换基, 因此我们可以尝试构造原系数域的扩域, 扩大系数域的阶数, 使其满足条件. 多项式系数使用扩域后, 由于其阶N 无法满足N −1 是2 的幂次这一条件, 因此多项式的长度也无法构造成2 的幂次, 基2 快速变换无法进行. 因此, 我们对多项式长度进行质因子分解, 使用复合基快速NTT 变换来达到与基2 快速变换接近的指数级加速效果.
4.1 扩域构造方法及证明
设Zq为原多项式的系数域, 其中q 是一个小于多项式长度N 的素数. 按照如下方法构造Zq的扩域ZPq:
• 元素集合: {[a,b]|a ∈Zq,b ∈Zq};
• 加法规则: [a,b]+[c,d]=[a+c,b+d];
• 乘法规则: [a,b]×[c,d]=[ac −bd,ad+bc].下面我们将给出这种构造方法的证明. 首先, 证明ZPq是一个域.
• 证明{ZPq,+} 是交换群:
(1) 依据ZPq上的加法定义可知其满足封闭性和结合律.
(2) {ZPq,+} 上存在唯一单位元(即ZPq的零元)[0,0]: [0,0]+[a,b]=[0+a,0+b]=[a,b].
(3) {ZPq,+} 上任意元素存在逆元: −[a,b]=[−a,−b].
(4) ZPq上加法满足交换律: [a,b]+[c,d]=[a+c,b+d]=[c+a,d+b]=[c,d]+[a,b].
• 证明{ZPq−{[0,0]},×} 是交换群:
(1) 依据ZPq上的乘法定义可知其满足封闭性.
(2) ZPq上乘法满足结合律:
(3) {ZPq−{[0,0]},×} 上存在唯一单位元[1,0]: [1,0]×[a,b]=[1a −0b,0a+1b]=[a,b]
(4) {ZPq−{[0,0]}} 中任意元素[a,b] 存在乘法逆元[a,b]−1=[a(a2+b2)−1,−b(a2+b2)−1]
(5) ZPq上乘法满足交换律: [a,b]×[c,d]=[ac −bd,ad+bc]=[ca −db,cb+da]=[c,d]×[a,b]
• 证明{ZPq,+,×} 满足乘法分配律:

然后证明ZPq中存在一个子域与Zq同构. 这里我们取同构子域为Z′q= {[a,0]|a ∈Zq}, 同构映射为σ(a)=[a,0].
• 加法同构: σ(a)+σ(b)=[a+b,0]=σ(a+b)
• 乘法同构: σ(a)×σ(b)=[ab −0,0a+0b]=[ab,0]=σ(ab)
扩域构造完成后, 其阶必须要大于原系数域的阶, 这样才能比原系数域支持更长的多项式数论变换.表1 列出了q 取128 至256 之间的素数时, ZPq域的阶数及生成元r 的参考取值.

表1 由小模数素域生成扩域时不同模数下的部分参数Table 1 Some parameters of different modulus while generating extension field with small modulus field
从表中可以看出, 素数域可以用扩域方法提高阶数, 从q 提升至N = q2, 且可从扩域中找到阶数为N −1 的生成元. 这其中有部分参数取值(如q = 251 等) 可以为实际的多项式乘数论变换提供变换基.我们注意到, 虽然扩域生成元r 的阶数N −1 无法构造为2 的幂次, 但在部分参数取值下扩域阶数仍然可以分解成比较小的质因子, 从而实现快速数论变换. 在下一节中, 我们介绍使用混合拆分的方法来实现扩域下的快速数论变换.
4.2 复合基快速数论变换
当多项式长度是2 的幂次时, 可以通过不断进行折半的方法实现快速数论变换, 称为基2 快速变换;而当多项式长度可以分解成多个不同的质因子时, 同样可以通过3 等分、5 等分等方式进行快速变换, 称为复合基快速数论变换. 与FFT 类似, 拆分方式分为时域拆分(DIT) 和频域拆分(DIF) 两种, 其中时域拆分从计算结果出发进行拆分, 频域拆分则是从输入数据出发进行拆分. 式(7)是使用DIT 方法的折半定理公式, 式(8)则是使用DIF 方法的折半定理公式. 图2 和图3 展示了这两种方法局部蝶形图的区别.


图2 8 点NTT 快速变换DIT 拆分示意图Figure 2 DIT of 8 points’ fast NTT

图3 8 点NTT 快速变换DIF 拆分示意图Figure 3 DIF of 8 points’ fast NTT
对于FFT 来说, 由于离散傅里叶变换和逆变换的对称性, 正变换和逆变换DIT 的公式结构相同, 正变换和逆变换DIF 的公式结构也相同. 但对于NTT 来说, 正变换和逆变换的公式并不是对称的(注意式(5)和式(6)中r 的存在), 因此正变换和逆变换的DIT 和DIF 公式各不相同, 我们总共需要推导4 个拆分公式. 设将长度为n 的变换分解为a 个长度为n′的子变换, 则这四个拆分公式分别如式(9)、式(10)、式(11)、式(12)所示, 其推导过程见附录.
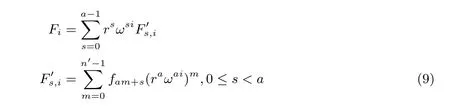
(2) 正变换DIF: 拆分成a 个子变换, 第b 个子变换的输入值为则有
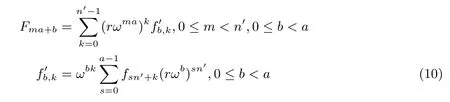

(4) 逆变换DIF: 拆分成a 个子变换, 第b 个子变换的输入值为, 则有

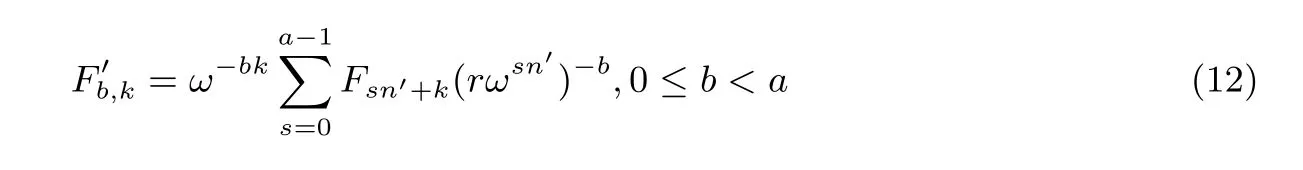
反复使用这种变换拆分方法可以将一个数论变换或逆变换拆成数级乘累加结构的蝶形图. 例如, 长度为45的NTT 变换可以拆成3 个15 点的子变换, 每个子变换又可以拆成3 个5 点的子变换. 这种拆分方法与图1 所示的基2 快速变换类似, 只不过基2 快速变换每次只拆成两个子变换, 而复合基快速变换的拆分是根据多项式长度的质因子分解进行拆分. 图4 给出了一个15 点NTT 用DIT 方式拆分成两级乘累加结构的蝶形图(未标注乘加系数). 由于每级乘累加结构的乘法计算量正比于(a −1)n(n 是多项式总长度, a 是拆分数), 因此我们在选择多项式长度时需要尽可能选择能够分解为较小质因子的值.

图4 15 点NTT 快速变换DIT 蝶形图Figure 4 Butterfly chart of DIT of 15 points’ fast NTT
5 效果验证
使用快速NTT 变换进行多项式环乘法的流程图如图5 所示. 该计算过程由两个正变换、一个逆变换和一个点值乘法组成, 其中点值乘法的复杂度是O(n)(n 为多项式长度). 由于模乘是多项式环乘法中最消耗计算资源的运算单元, 因此我们以模乘数目作为指标来进行性能比对. 首先, 直接法实现的多项式乘法消耗的模乘数目为LM= n2. 基2 快速变换中每个变换花费的模乘数目是2n log2n, 因此总的模乘数目是n+6n log2n. 类似地, 基k 快速变换中每个变换花费的模乘数目是2(k −1)n logkn. 对于复合基变换来说, 我们构造一个等效底数β, 使其模乘数目满足通式2(β −1)n logβn. 这个等效底数与多项式长度的质因子分解有关, 分解出的质因子越大则β 越大. 对于扩域法进行的快速变换, 每个扩域模乘相当于4 个原素数域的模乘(参见第4.1 节). 因此, 使用扩域复合基快速数论变换的多项式乘法花费的模乘数目公式如下:

以LAC 算法的模数251 为例, 表2 中列出了多项式长度N 取不同值时扩域快速变换的加速效果. 可以看出, 扩域法能够对多项式环乘法的加速起到一定作用. 在加密算法常用的多项式长度范围内能提供数倍的加速效果, 而在多项式长度取该模数支持的最大值时, 可提供数十倍的效果.
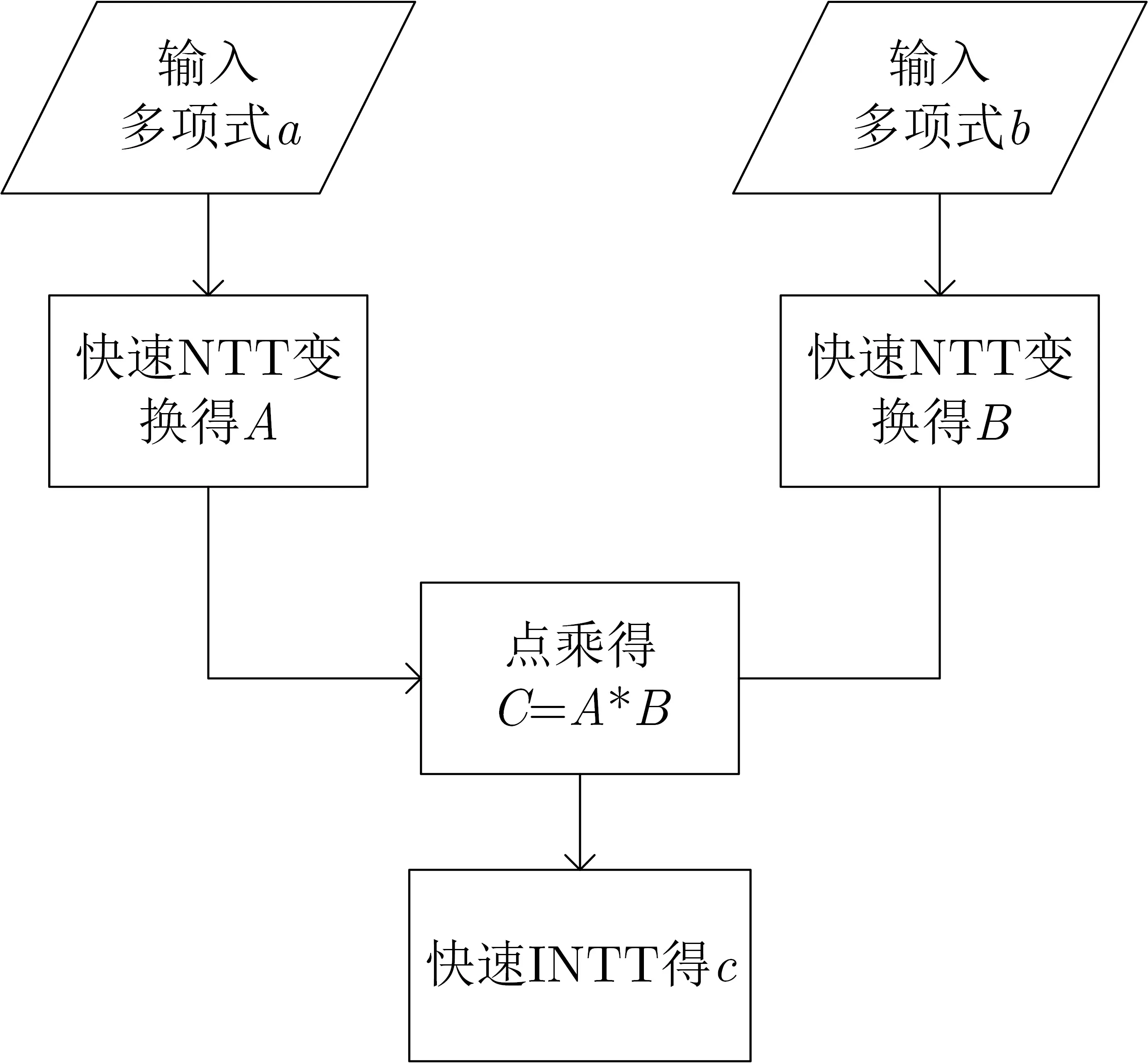
图5 快速NTT 法实现多项式乘的步骤Figure 5 Steps of polynomial multiplication with fast NTT

表2 模数q=251 时扩域快速NTT 实现多项式乘法的理论加速效果Table 2 Theoretic accelerating effect of fast NTT on extension field with q=251
6 总结
本文探索了小模数多项式乘法使用数论变换进行加速的可行性. 我们设计了一种多项式系数域的扩域方法, 并推导了复合基快速数论变换的拆分公式, 使得小模数多项式乘法也能够使用快速数论变换来进行加速. 通过编写代码验证, 证明其相比直接法实现的多项式乘, 能够提供一定的加速效果, 在特定场景下有较好效果.

