图像压缩感知在信源信道联合编码系统中的应用

刘叙含, 张尚卓, 黎海青, 张伟杰, 张建松

图像压缩感知在信源信道联合编码系统中的应用

刘叙含1, 张尚卓2, 黎海青1, 张伟杰1, 张建松1

(1. 西安现代控制技术研究所, 陕西 西安, 710065; 2. 西北工业大学 航海学院, 陕西 西安, 710072)

提出了一种将基于离散小波变换的图像压缩感知应用在信源信道联合编码系统中的方法。该方法将双重不等差错保护与码率动态分配机制相结合, 在信源编码部分, 根据图像小波变换后各频带所包含重构信息量的差异, 利用压缩感知算法进行不等压缩, 产生渐进性的信息流, 信息流通过Huffman熵编码后成为适合信道传输的二进制码流; 在信道编码部分, 根据信源编码后二进制码流的渐进性信息, 动态分配Turbo编码码率, 从而实现信道的不等差错保护。该联合编码方法在信道资源受限的情况下, 可对资源进行优化分配, 达到良好的端到端通信效果。以标准灰度图像Lena图为例, 编码后通过高斯白噪声信道, 仿真结果为: 当信噪比为4 dB时, 图像重构均方误差为0.061 6, 重构性能良好; 同时, 系统获得了高达4:1的压缩比, 系统耗能减少, 传输效率增加。

压缩感知; 小波变换; 源信道联合编码; 不等差错保护; 码率分配

0 引言

传统的通信系统根据Shannon分离原理[1]将信源编码和信道编码分别设计, 互不相关。信源编码的目标是去除信息冗余, 输出统计独立的编码比特流, 从而达到最大压缩比, 尽可能接近率-失真(rate-distortion)界限; 而信道编码的实质则是通过增加冗余, 提高信息对信道噪声的鲁棒性, 使其具有一定的检错和纠错能力, 能够无误差地到达接收端进行信号重建。然而, 对于实际应用中的大多数通信系统(例如蜂窝通信、一对多的广播通信、多径严重的水声通信等)而言, 都无法满足分离原理实现系统最优性能的前提条件[2], 这促使了信源信道联合编码(joint source channel coding, JSCC)理论[3]的产生和发展。

JSCC是一种综合考虑信源、信道因素的编码设计方法, 在性能和复杂度之间寻找最优解, 通过优化分配信道资源, 在恶劣的无线信道下获得最优的端到端通信效果。国外关于JSCC领域的研究起步很早。1977年, Elience首次提出JSCC整体方案, 早期主要是通过比较各种可能的信源信道比特分配方式寻求失真最小的一种。Modes- tino等[4]提出将JSCC应用于静止图像上, 将二维差分脉冲编码调制(differential pulse code modulation, DPCM)编码、树编码及二维离散余弦变换(discrete cosine transform, DCT)编码等信源编码和信道卷积码级联, 给信源信道分配不同码率。此后, 该方法被扩展到其他由图像编码和信道纠错码组成的系统中。

压缩感知(compressed sensing, CS)作为近年来信息处理领域的一大理论[5], 突破了奎斯特采样定理关于采样速率必须达到信号最高频率的2倍或2倍以上才能精确重构原始信号的局限, 实现了数据压缩采样的同时进行。在信源编码方面具备传统压缩编码难以获得的高压缩率和精确的重构性能。

文中将CS理论应用在JSCC系统中, 提出了一种将基于小波变换的图像压缩感知应用在信源信道联合编码中的算法, 以双重不等差错保护与码率动态分配相结合, 建立一套完备的编码系统, 尤其在信道资源有限的情况下可对信道资源进行优化分配, 达到良好的端到端通信效果。

1 CS理论

传统的奈奎斯特采样定理几乎决定了所有离散信号的获取方式。然而, 随着信息量的井喷式增长, 信号的带宽越来越宽, 所要求的采样速率和处理速度也越来越高, 基于奈奎斯特采样定理的离散信号获取方式遇到了瓶颈。

Candes 和Donoho 在2006年提出了CS理论, 其核心思想是将压缩与采样合并进行[5-6]。该理论指出, 只要信号是可压缩的或在某个变换域是稀疏的, 那么就可以利用一个与变换基不相干的观测矩阵将高维信号投影到一个低维空间上, 可以证明这些少量的投影包含了重构信号所需的足够信息[7]。在该理论框架下, 采样速率不取决于信号的带宽, 而是取决于信息在信号中的结构和内容。

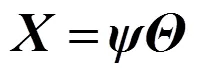
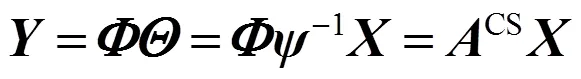
2 基于小波变换的图像压缩感知

以标准的灰度图像Lena图为例, 如图1所示, 详细介绍文中设计的基于小波变换的图像压缩感知算法。

图1 标准灰度图像Lena图

2.1 图像信号的稀疏表示

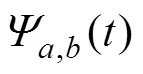
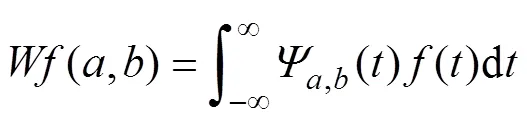
首先沿水平方向进行一次变换, 分解得到垂直方向的低频分量和高频分量; 再沿垂直方向进行一次变换, 即得到4个分量, 分别为水平低频垂直低频分量LL、水平低频垂直高频分量LH、水平高频垂直低频分量HL和水平高频垂直高频分量HH, 如图2所示。图像从时域映射到频域时, 大部分能量集中在低频, 少量的非重要信息集中在高频。标准灰度图像Lena图二维小波变换后, 主要信息集中在左上角的水平低频垂直低频分量LL, 非重要的边缘信息集中在其余3个分量[11], 如图3所示。

2.2 图像信号观测

图像信号的观测实质上就是图像信号的压缩过程[12-13]。文中采用高斯观测矩阵进行观测, 根据图像小波变换后4个分量所包含图像信息量的不同, 进行不等压缩: 完全保留低频LL分量, 大量压缩LH、HL和HH分量。这样的不等压缩方法与常用的无针对性的压缩方法相比, 由于完全保留了图像重构所需的低频重要信息, 所以在同样的压缩比条件下可以获得更加精确的重构图像。当压缩比为2:1时: 图4是采用不等压缩方法得到的重构图像; 图5是采用同等压缩后得到的重构图像, 由于它的低频重要信息也受到了同等程度的压缩, 损失了重构所需的重要信息, 所以无法重构。

图3 Lena图像各频率分量携带信息示意图

图4 采用不等压缩法的重构图像

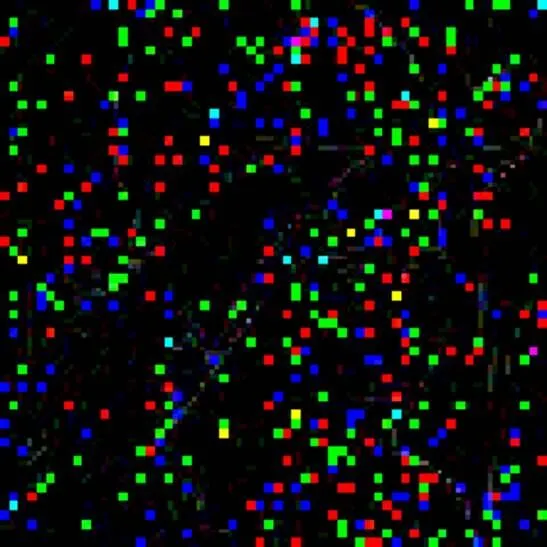
图5 采用均等压缩法的重构图像

3 基于图像CS的JSCC系统

基于小波变换的图像CS在JSCC系统中的应用模型如图6所示, 主要由信源编码、信道编码、信道译码和信源译码四部分组成[15]。

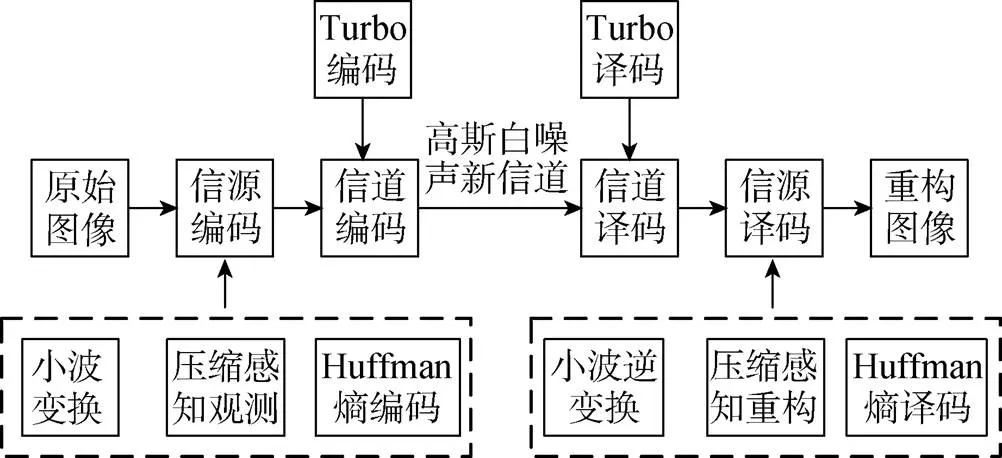
图6 JSCC系统模型

信源编码采用不等压缩思想, 主要包括二维小波变换、信号观测和Huffman熵编码三部分。首先, 图像经过二维离散小波变换后得到4个频域分量LL、LH、HL和HH, 如图2所示。其次, 利用CS对4个频域分量进行不等压缩, 即观测过程。将压缩后的信息排列成渐进性的信息流, 如图7所示。低频分量LL作为重要信息排列在信息流前端, 其余3个压缩后的分量依次排列。最后, 采用Huffman无损编码技术将渐进性的信息流转换为适合信道传输的二进制码流。至此, 系统得到了有利于信道不等差错保护的渐进性二进制码流。

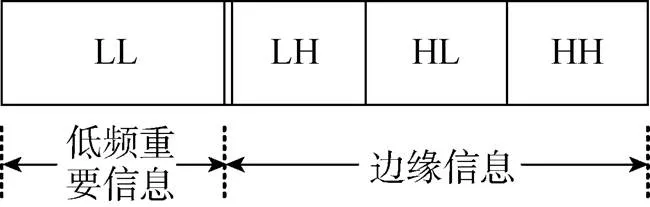
图7 渐进性信息流

信道编码采用Turbo码, 又称并行级联卷积码(parallel concatenated convolutional code, PCCC), 具有接近Shannon理论极限的译码性能。理论上可以通过改变Turbo码的删除模式得到任意码率的码字, 这正是文中所设计的联合编码系统选择Turbo码的原因。根据二进制码流的渐进性动态分配码率, 即采用低码率保护码流前端的LL分量、高码率保护其余3个分量, 从而实现码流的不等差错保护。这样可在信道资源受限的情况下将资源优先分配给重要信息码字, 并且在信道条件恶劣时着重保护重要信息码字。

Turbo译码时采用迭代思想, 常用的有最大后验概率 (Maximum A Posteriori, MAP)算法及其简化算法Log-MAP算法、Max-Log-MAP算法等[16]。

信源译码部包含Huffman译码、CS重构算法、小波逆变换三部分。Huffman译码的思想是根据其编码时建立的Huffman树进行逆向追踪。CS重构算法采用匹配追踪(matching pursuit, MP)算法[14]。

4 仿真试验

2) 利用CS对4个频域分量进行不等压缩, 得到渐进性信息流;

3) 利用Huffman熵编码将渐进性信息流转化为渐进性二进制码流, 如图7所示;

4) 动态调节Turbo码的码率, 对二进制渐进码流进行不等差错保护, 码流前端的LL分量采用1/3的码率, 其余分量采用1/2的码率;

5) 通过高斯白噪声信道;

6) Turbo译码采用Log-MAP算法, 迭代5次;

7) 压缩感知重构算法采用MP算法。

图8 压缩比为8:1时的重构图像

图9 压缩比为5:1时的重构图像

图10 压缩比为4:1时的重构图像

图11 不同压缩比条件下Lena图重构均方误差

5 结束语

与传统的JSCC系统相比, 将基于小波变换的图像CS应用在JSCC系统中, 发挥了CS相对于传统压缩编码压缩比高、重构精确的优势; 其次, Huffman编码与CS构成了双重压缩, 可获得更高的压缩比; 传统基于不等差错保护的JSCC系统仅仅是在信道编码实现不等保护, 然而文中将不等差错保护的理念应用在整个系统中, 对信源进行不等压缩、对信道进行不等保护, 实现了双重不等差错保护, 更加充分地利用了信道资源; 码率动态分配机制可行, 只需动态分配1次码率, 减小了系统复杂度和运行时间。

由于CS重构算法主要是迭代法, 处理庞大数据量时的系统延时是下一步研究的主要问题, 未来计划开展CS重构算法优化和基于CS的通信系统优化研究。

[1] Shannon C E. Coding theorems for a Discrete Source with a Fidelity Criterion[J]. IRENAT. Conv. Rec. 1959, 7: 142-163.

[2] Tu G F. Studies and Advances on Joint Source-Channel Encoding/Decoding Techniques in Flow Media Communications[J]. Science China, Information Sciences, 2010, 5(1): 1-17.

[3] Fresnedo O. Low-Complexity Near-Optimal Decoding for Analog Joint Source Channel Coding Using Space-Filling Curves[J]. IEEE Communications Letters, 2013, 17(4): 745-748.

[4] Modestino J W, Daut D G. Combined Source-Channel Coding of Images [J]. IEEE Trans. Common, 1979, 27(11): 1644-1659.

[5] 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 425-434.Dai Qiong-Hai, Fu Chang-Jun, Ji Xiang-Yang. Research on Compressed Sensing[J]. Chinese Journal of Computers, 2011, 34(3): 425-434.

[6] 尹宏鹏, 刘兆栋, 柴毅, 等. 压缩感知综述[J]. 控制与决策, 2013, 10(28): 1441-1453.Yin Hong-peng, Liu Zhao-dong, Chai Yi, et al. Survey of Compressed Sensing[J]. Control and Decision, 2013, 10(28): 1441-1453.

[7] Candès E, Wakin M. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.

[8] 沈明欣. 基于压缩感知理论的图像重构技术研究[D]. 南京: 南京航空航天大学, 2010.

[9] 陈明惠, 王帆, 张晨曦, 等. 基于压缩感知的频域OCT图像稀疏重构[J]. 光学精密工程, 2020, 28(1): 189-199.Chen Ming-hui, Wang Fan, Zhang Chen-xi, et al. Sparse Reconstruction of Frequency Domain OCT Image Based on Compressed Sensing[J]. Optics and Precision Engineering, 2020, 28(1): 189-199.

[10] 赵敏. 基于新特征和小波变换的图像压缩编码算法[D].南京: 南京邮电大学, 2019.

[11] 周鹏, 孟晋. 基于分块压缩感知算法的图像重构技术[J]. 九江职业技术学院学报, 2019(3): 15-16, 12.Zhou Peng, Meng Jin. On Image Reconstruction Technology Based on Blocking Compressed Sensing Algorithm[J]. Journal of Jiujiang Vocational and Technical College, 2019(3): 15-16, 12.

[12] 王钢, 周若飞, 邹昳琨. 基于压缩感知理论的图像优化技术[J]. 电子与信息学报, 2020, 42(1): 222-233.Wang Gang, Zhou Ruo-fei, Zou Yi-kun. Research on Image Optimization Technology Based on Compressed Sensing[J]. Journal of Electronics & Information Tech- nology, 2020, 42(1): 222-233.

[13] 刘叙含, 申晓红, 姚海洋, 等. 基于帐篷混沌观测矩阵的图像压缩感知[J]. 传感器与微系统, 2014, 33(9): 26-31.Liu Xu-han, Shen Xiao-hong, Yao Hai-yang, et al. Image Compressed Sensing Based on Tent Chaos Measurement Matrix[J]. Transducer and Microsystem Technologies, 2014, 33(9): 26-31.

[14] 金立强. 基于极化码的信源信道联合编码研究[D]. 北京: 北京邮电大学, 2019.

[15] 刘叙含. 基于图像压缩感知的信源信道联合编码系统研究[D]. 西安: 西北工业大学, 2015.

[16] 黄剑婷. 低复杂度LDPC码译码算法研究与实现[D]. 哈尔滨: 哈尔滨工业大学, 2019.

1. 朱志鹏, 朱志宇. 一种基于双目视觉的水下导引光源检测和测距方法. 2021, 29(1).

2. 张韫峰, 李娟, 黎明. 基于图像处理的水下海参识别和定位方法. 2021, 29(1).

3. 岳雷, 姜春华, 罗松, 等. 低频宽带多波束声呐系统设计及试验研究. 2020, 28(1).

4. 朱兆彤, 付学志, 胡友峰. 一种利用迁移学习训练卷积神经网络的声呐图像识别方法. 2020, 28(1).

5. 杜金香, 许恒博. 基于空时频联合处理的水下目标宽带声成像. 2019, 27(4).

6. 杜雪, 廖泓舟, 张勋. 基于深度卷积特征的水下目标智能识别方法. 2019, 27(3).

7. 张伟, 李子轩, 宫鹏, 等. UUV接驳单目视觉导引灯阵定位方法. 2019, 27(3).

8. 王其林, 王宏健, 李庆, 等. 侧扫声呐图像特征提取改进方法. 2019, 27(3).

9. 苏梦娜, 梁红, 杨长生. 基于SCAT模型的水下多目标高分辨仿生成像方法. 2019, 27(2).

10. 张红梅, 陈明杰, 刘洪丹, 等. 基于CS和随机声呐阵列的水下目标方位估计. 2018, 26(6).

11. 范威, 朱代柱, 张德泽, 等. 混合高斯模型和Radon变换用于声呐图像背景抑制. 2018, 26(5).

12. 何心怡, 高贺, 卢军, 等. 逆合成孔径成像在鱼雷真假目标识别中的应用及展望. 2017, 25(4).

13. 张远彪, 朱三文. 有缺陷的多接收阵合成孔径声呐成像技术. 2015, 23(4).

14. 王小舟, 张严, 胡友峰. 同步误差下OFDM稀疏信道估计. 2013, 21(2).

15. 陈玉凤, 黄建国, 苏建军. 基于稀疏重建和压缩感知波束形成的高分辨DOA估计. 2013, 21(2).

The Application of Image Compressed Sensing in Joint Source-Channel Coding System

LIU Xu-han1, ZHANG Shang-zhuo2, LI Hai-qing1, ZHANG Wei-jie1, ZHANG Jian-song1

(1. Xi’an Modern Control Technology Research Institution, Xi’an 710065, China; 2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

This paper proposes a method which applies image compressed sensing based on the discrete wavelet transform(DWT) in the joint source-channel coding system. This method combines the double unequal error protection and dynamic rate allocation mechanism. According to the difference in the sub-band reconstruction information of each frequency after DWT of the image, unequal compression is performed using the compressed sensing(CS) algorithm to produce a progressive information flow in the source coding part. Consequently, the information flow is converted into binary codes which is comparably suitable for the channel transmission after the Huffman entropy coding. The rate of Turbo is distributed based on the progressive bit stream dynamically in the channel coding part, to achieve the unequal error protection of the channel. During instances when the channel resources are limited, the channel resource allocation can be optimized to achieve good end-to-end communication performance. Performing a simulation of the standard gray scale image of Lena and passing through the white Gaussian noise channel after coding, the result is as follows: When the SNR is 4 dB, the image reconstruction mean square error is 0.061 6 with good reconstruction performance. Meanwhile, the system obtains the compression ratio up to 4:1, reduces the system energy consumption and increases the transmission efficiency.

compressed sensing; wavelet transform; joint source channel coding; unequal error protection; rate allocation

TJ630.34; TN911.73

A

2096-3920(2021)02-0218-06

10.11993/j.issn.2096-3920.2021.02.013

刘叙含, 张尚卓, 黎海青, 等. 图像压缩感知在信源信道联合编码系统中的应用[J]. 水下无人系统学报, 2021, 29(2): 218-223.

2020-01-17;

2020-04-22.

刘叙含(1990-), 女, 硕士, 工程师, 主要研究方向为压缩感知及信源信道联合编码.

(责任编辑: 陈 曦)