一种多光学浮标联合定位算法及仿真
郭建忠, 孙 健, 王凯帅
一种多光学浮标联合定位算法及仿真
郭建忠1, 孙 健2, 王凯帅2
(1. 海装重大专项装备项目管理中心, 北京, 100161; 2. 中国船舶工业系统工程研究院, 北京, 100094)
为解决单、双光学浮标无法获得目标全要素信息的问题, 文中基于声学目标运动要素解算技术, 提出了一种多光学浮标联合定位算法, 建立了包含浮标定位误差、观测时间误差和光学观测模糊误差的光学浮标观测数学模型, 利用蒙特卡洛仿真方法给出了考虑上述误差并针对机动目标不同数量光学浮标的定位精度指标, 同时分析了各因素对多浮标联合定位的影响。文中研究为光学浮标的工程应用提供了数据支撑。
光学浮标; 机动目标; 定位精度
0 引言
光学浮标是一种集合惯性导航、信号采集与处理、电机控制、微电子技术与数字图像识别处理等诸多技术, 实现目标识别和监测的复杂设备。近年来, 随着电子信息技术的高速发展, 光学浮标技术取得了巨大进展并且越来越广泛地应用在军用领域, 可以为无人水下航行器对视界范围内的敌水面舰艇攻击提供有效的目标指示[1]。由于体积限制等因素, 单个光学浮标瞬时定位能力较弱, 需要依靠定位算法利用信息的时间累计获得满足使用要求的空间定位精度。
定位算法有参数估计和状态估计两类, 参数估计类算法包括线性最小二乘、非线性最小二乘、极大似然估计以及辅助变量最小二乘等算法; 状态估计类算法包括线性卡尔曼滤波、非线性卡尔曼滤波、无迹卡尔曼滤波、容积卡尔曼滤波和粒子滤波等算法。状态估计类算法均属于广义贝叶斯算法, 要求有目标的先验知识, 即确定目标的初始似然位置后进行滤波, 以获得一定条件下的目标最大后验概率解, 最大后验概率解受初始似然位置的影响较大。参数估计类算法不需要目标的先验知识, 但需要对目标测量参数进行一定时间累积后分析目标的运动参数[2-6]。
实际工程应用中, 对于可以直接获得较高精度目标距离和目标方位的有源传感器(如雷达、激光测距仪), 一般采用状态估计类算法进行目标定位; 对于无法获取目标距离或获取目标距离精度较差的无源传感器, 一般采用参数估计类算法进行目标定位。光电浮标属于被动无源传感器, 获取目标距离的主要方式是焦平面凝视手段, 在设备尺寸的限制下, 获取距离精度差, 无法达到使用要求。
浮标定位工程化研究方面, 刘忠、石章松等[7-9]针对声学多节点被动定位, 将节点拓扑结构分为了集中式和分布式两大类, 并分别给出了相关定位算法; 杜选民等[10]研究了多声基阵联合的无源纯方位算法, 并给出相关的研究结论。目前, 光学浮标领域的工程化研究主要集中在利用浮标进行海洋环境检测等遥感领域, 将其利用在目标定位与跟踪领域的文献很少[11]。
为满足武器的实际使用需求, 文中借鉴声学目标运动要素解算的技术, 提出了一种工程化的多光学浮标联合定位方法, 并对实际测量过程中的浮标定位误差、光学测量误差、光学模糊效应和测量时戳误差进行了建模和仿真分析, 给出存在这些误差条件下光学浮标阵对机动目标的定位精度指标。
1 联合定位数学模型
按照系统可观测性理论, 单个光学浮标仅依靠对目标方位信息的持续观测获得目标航向C和距离速度比(0/V)信息, 无法获得目标的全要素信息(即目标初距0、目标速度V以及C)。
为达到对目标的全要素定位, 至少需要2个光学浮标联合工作, 利用双浮标分别测量目标方位与浮标之间的孔径尺度特征, 通过三角定位原理获得目标的概略位置。但在目标运动到双浮标连线附近时, 由于测量方位一致, 定位算法无法收敛, 且在目标发现自身被攻击时进行机动后, 双浮标一般无法达到提供攻击目标指示的需求, 因此需多个浮标综合使用以实现该战术目的。
以3光学浮标为例说明多光学浮标联合定位的滑窗非线性最小二乘法数学原理, 该原理可以扩展为多浮标应用, 却不局限于3浮标, 如图1所示。
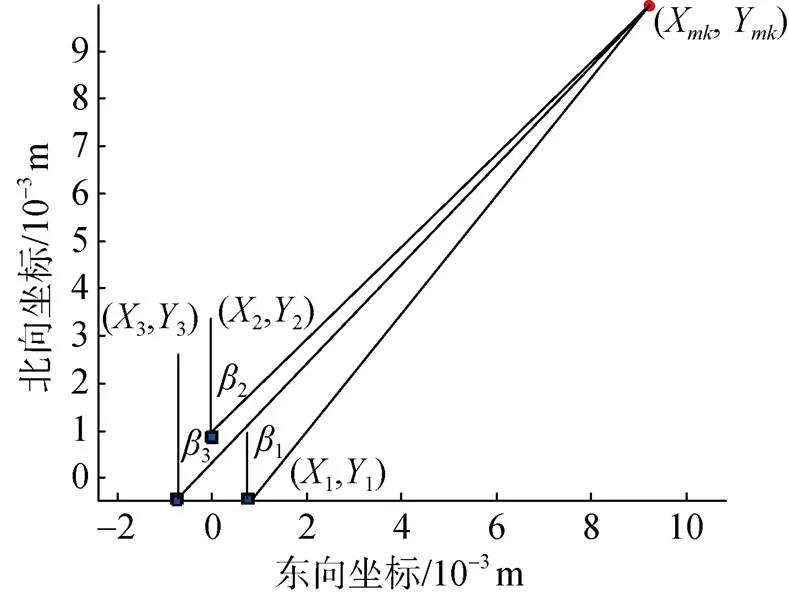
图1 多光学浮标联合定位示意图



将式(2)代入式(1)并进行线性化, 可得观测方程的雅各比矩阵

其中
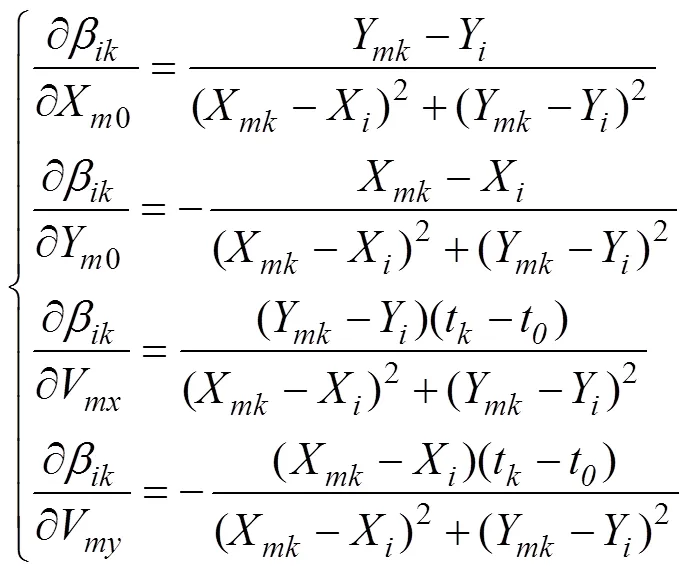
利用非线性最小二乘法解算目标运动要素的迭代算法如下。

2 误差模型
2.1 方位测量误差
方位测量误差包括两部分, 一部分由传感器测量的随机性引起, 另一部分由光学设备提取目标方位的模糊性引起。
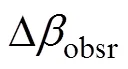

图2 光学浮标测量光学模糊误差示意图
考虑测量模糊最不利的情况, 测量真方位上光学模糊误差, 将方位测量扩展为虚线所示的随机方位, 随机方位服从均匀分布, 且目标离浮标越近, 均匀分布的边界越大, 光学模糊测量误差
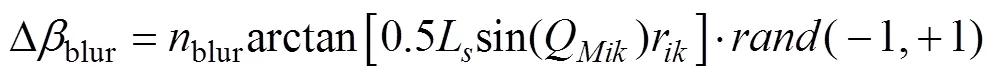
最终目标的观测向量

式中,为光学浮标从节点通过无线自组织网络回报主节点的方位数量。
2.2 位置测量误差


海流相关影响需加入位置误差中, 即

2.3 时间测量误差
时间测量误差主要是由从浮标节点发送和主浮标节点接收的嵌入式计算机处理时间、传输延迟以及无线自组织网络调度延迟引起, 无线自组织网络采用令牌环式时分多址协议进行调度[13], 浮标节点序号由母船分配, 主浮标出水后以5 s为周期向从浮标发送同步信号, 各从浮标接收到同步信号后, 按照节点序号的时隙发送自身位置和探测目标信息, 节点令牌持续时间为0.5 s, 随机误差0.1 s, 具体误差

式中: 为-0.1~0.1的均匀分布, 表示从节点广播自身信息的误差; 为网络及嵌入式计算机参数, 表示浮标时分多址的定时误差性能, 时分多址如图3所示。
3 联合定位流程及浮标分布结构
多光学浮标联合定位信息流程如图4所示。母船分配浮标序号后部署多个有动力浮标入水, 浮标入水后向母船规定的位置航行。若从节点浮标先出水, 则等待主浮标的同步码信号, 主浮标出水工作后按照约定的周期广播同步码, 从节点浮标按照自身序号信息在收到同步码后延迟预定时隙广播自身位置和探测目标的方位信息, 主浮标累积该信息, 以120 s为周期随同步码广播利用累积信息计算的目标运动参数及自身位置, 各浮标接收该信息后进行空间对准并获取目标位置。
母船应按照正多边形布置浮标, 若浮标自带动力可航行, 各浮标航路终点的拓扑结构为正多边形。按照测量孔径原理, 浮标的最优布置位置呈直线等间隔布置且直线方向与目标航向一致, 这种布置能保证测量精度达到最优, 但实际使用时目标航向是未知的, 在这种条件下, 最优的拓扑结构仍为正多边形布置, 原因如下:

图4 多光学浮标联合定位信息流程图
1) 保证目标以任何航向航行或机动时, 浮标阵的综合孔径最大;
2) 若浮标无动力, 可最大程度节约布放母船的航行距离, 若浮标有动力, 可最大程度节约多个浮标总体的航行距离, 有利于浮标同时出水工作;
3) 各浮标综合通信距离最短, 有利于各浮标的无线自组织网络构建。
4 联合定位计算结果与分析
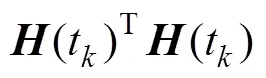
构建如下态势: 目标舰干舷+桥楼有效高度为20 m, 浮标高度为0.5 m, 浮标对目标探测距离约12 km, 母船分别释放不同数量浮标, 浮标正多边形布置, 孔径(浮标与相邻最近浮标的距离)均为1 000 m, 目标在浮标阵附近做正方形运动, 目标初距8 km, 处于浮标阵正北方向, 航向90°, 速度18 kn, 当目标距浮标阵中心距离大于12 km时, 目标右转向90°进行机动如图5所示。
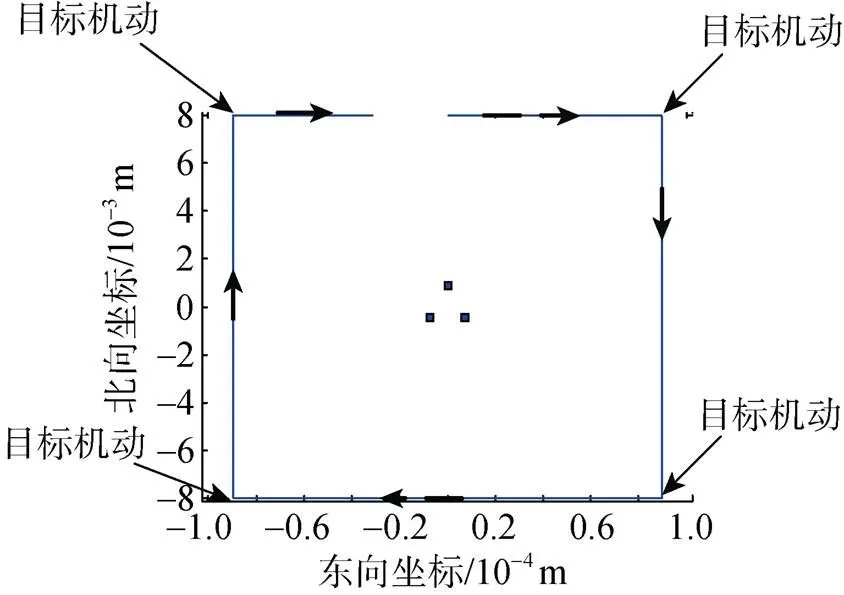
图5 多光学浮标联合定位仿真场景图
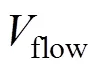
在方位测量随机误差一定的条件下, 影响光学定位的主要因素有光学对焦模糊(测量误差0.7°, 光学对焦模糊为1~5倍目标长度)、无线自组织网络时间误差(广播时间误差0.1~0.5 s)、浮标自身定位误差(2阶原点距为20 m), 分别分析上述各因素对目标定位的影响, 各因素的选取按照实际测量设备的性能选取。


图7 4浮标联合定位结果仿真效果图
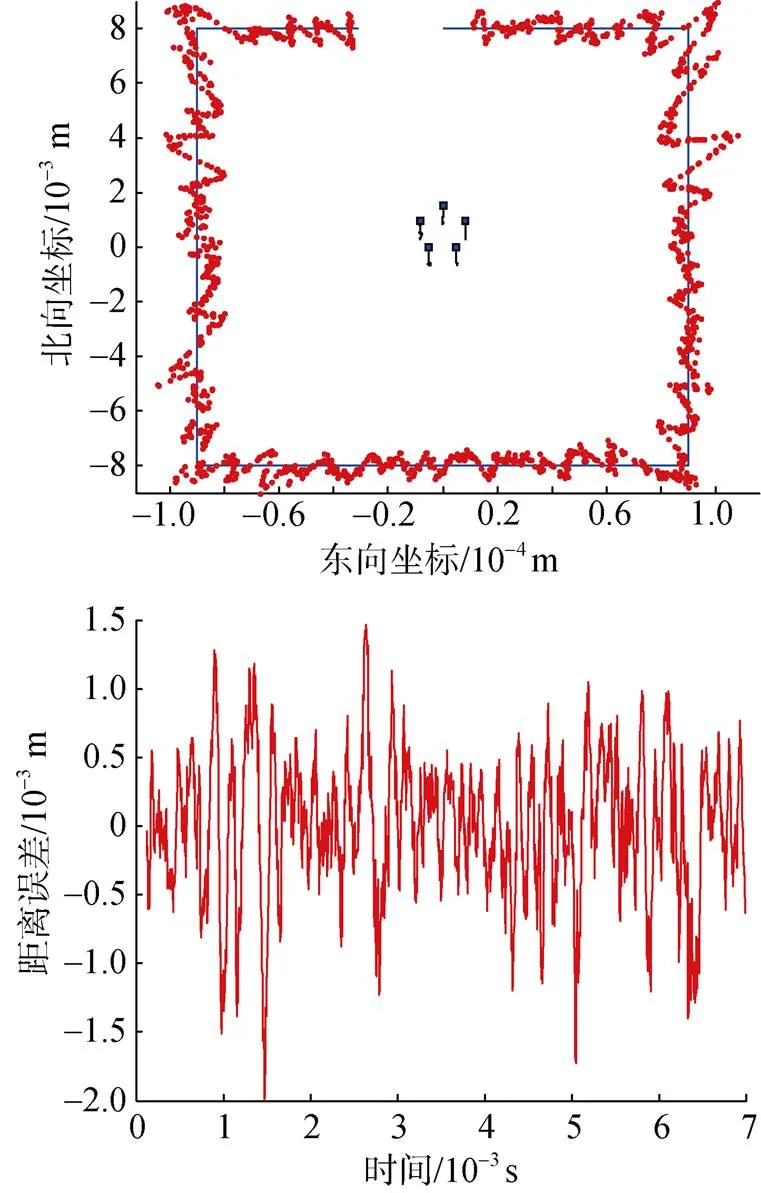
图8 5浮标联合定位结果仿真效果图
经过对表1~表3的分析, 可以得出以下结论: 影响光学浮标阵对目标定位的最主要因素为光学对焦模糊, 其次因素为浮标定位误差, 测量时间误差对目标定位影响最小, 实际设备研制中需最大程度解决光学对焦模糊对测量目标方位的影响。
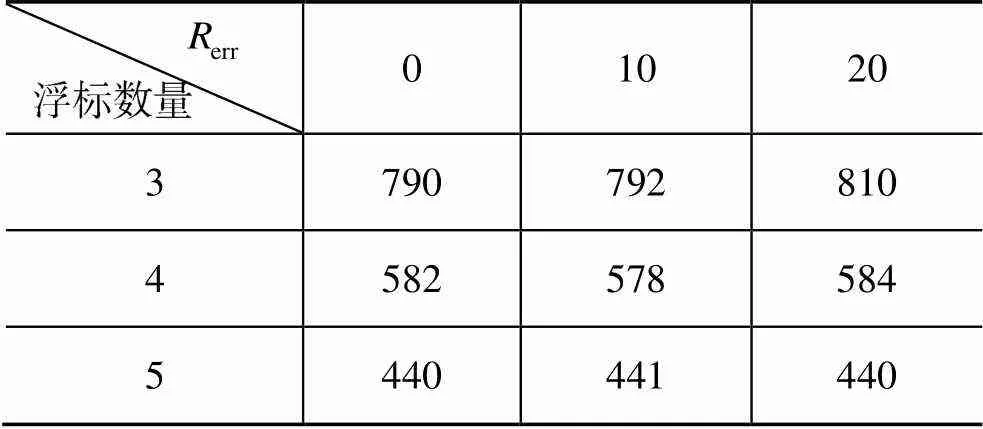
表1 北向东向定位误差影响下的浮标联合定位精度(m)
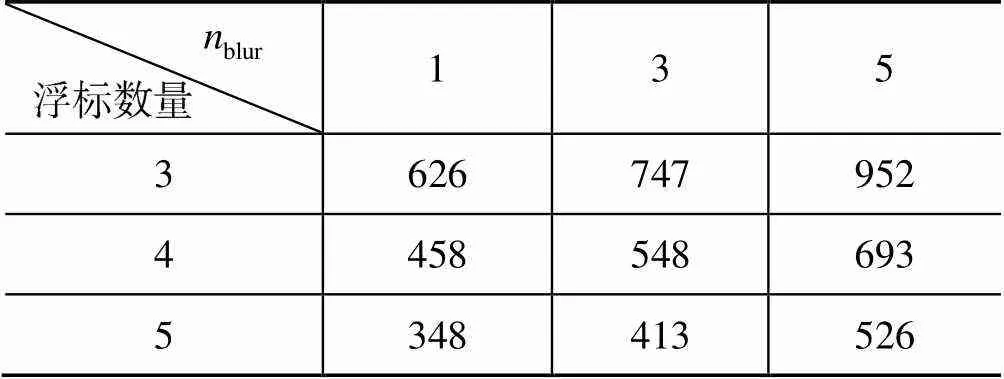
表2 光学模糊程度影响下的浮标联合定位精度(m)
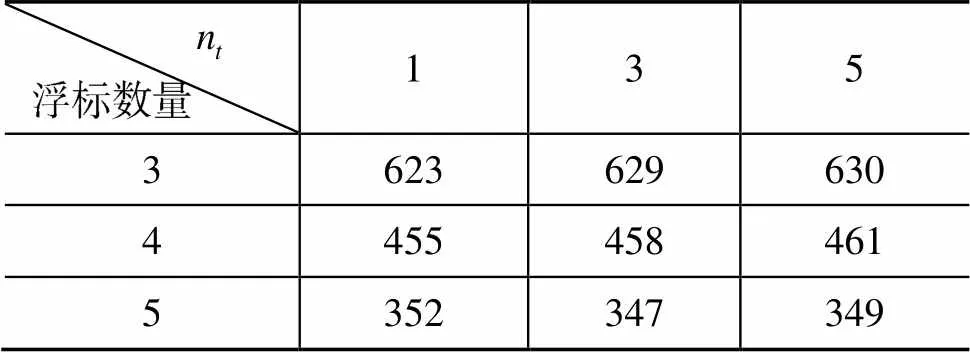
表3 时间测量误差影响下的浮标联合定位精度(m)
计算浮标阵在浮标设备指标最差条件下的定位精度。如表4所示。

表4 浮标设备指标最差条件下联合定位精度
5 结论
文中利用非线性最小二乘方法实现电浮标联合目标定位, 建立了方位测量误差、位置误差和时间测量误差与海流、网络传输时间、浮标定位精度和光学测量模糊的关系模型, 分析了海流、嵌入式计算机及无线自组织网络传输时间、GPS浮标定位、光学测量模糊等因素对多浮标联合定位的影响, 为光学浮标的应用提供技术支持。并得出如下结论:
1) 非线性最小二乘方法可以很好地回避多阵测量不确定点问题, 避免状态估计对先验知识的要求, 可以作为光学浮标联合定位的主要方法。
2) 滑窗时间设置与目标机动的快慢有关, 反应了浮标阵目标机动识别和要素估计精度的矛盾: 滑窗时间越大, 对定向定速目标估计精度越高, 但定位惯性较大, 对机动目标定位的灵敏度越弱; 滑窗时间小则会影响定位精度, 但对机动目标的灵敏度高。实际工程化过程中可根据无人水下航行器的航行速度范围选择滑窗时间。
3) 浮标布置为正多边形, 可使目标在视界的机动形式不会对定位精度造成较大影响, 定位的平均效果最好, 因此当不确定目标在视界内的航向时, 建议浮标按照正多边形布置。
4) 实际工程中设备误差大多以多种形式呈现, 部分设备在技术上的误差难以用正态分布来近似, 可能以均匀分布近似或在统计学上表现出较强的“厚尾效应”, 多种误差叠加的系统总体指标采用数学解析的方法进行分析相当困难, 此时可采用蒙特卡罗仿真的手段获得系统的数值指标为后续工程化提供较为详细的数据支撑。
[1] 马俊达. 海洋浮标光学稳定系统控制规律的研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
[2] Bar-Shalom Y, Li X. Rong, Kirubarajan T. Estimation with Application to Tracking and Navigation[M]. USA: Wiley-Interscience, 2001.
[3] John C, John J. Optimal Estimation of Dynamics Systems[M]. USA: CRC-Press, 2015.
[4] Johnston L, Krishnamurthy V. Derivation of a Sawtooth Iterated Extended Kalman Smoother via the AECM Algorithm[J]. IEEE Transactions on Signal Processing, 2001, 49(9):1899-1909.
[5] Rui Y, Chen Y Q. Passive Target Tracking by Unscented Filter[C]//Proceedings of IEEE International Conference on Industrial Technology. Goa-India: IEEE, 2000.
[6] Coates M. Distributed Particle Filter for Sensor Networks[C]//Third International Symposium on Information Processing in Sensor Networks, Berkeley USA: IEEE, 2004.
[7] 刘忠, 周丰, 石章松, 等. 纯方位目标运动分析[M]. 北京: 国防工业出版社, 2009.
[8] 薛锋, 刘忠, 石章松. 基于粒子滤波的传感器网络被动目标跟踪研究[J]. 仪器仪表学报, 2006, 27(z1): 314-315.Xue Feng, Liu Zhong, Shi Zhang-song. Target Passive Tracking in Sensor Networks Based on Particle Filter[J]. Chinese Journal of Scientific Instrument, 2006, 27(z1): 314-315.
[9] 薛锋, 刘忠, 曲毅. 无线传感器网络中的分布式目标被动跟踪算法[J]. 系统仿真学报, 2007, 19(15): 3499-3502.Xue Feng, Liu Zhong, Qu Yi. Decentralized Algorithm for Target Passive Tracking in Wireless Sensor Networks[J]. Journal of System Simulation, 2007, 19(15): 3499-3502.
[10] 杜选民, 姚蓝. 多基阵联合的无源纯方位目标运动分析研究[J]. 声学学报, 1999, 24(6): 604-610.
[11] 杨跃忠, 孙兆华, 曹文熙, 等. 海洋光学浮标的设计及应用试验[J]. 光谱学与光谱分析, 2009, 29(2): 565-569. Yang Yue-zhong, Sun Zhao-hua, Cao Wen-xi, et al. Design and Experimentation of Marine Optical Buoy[J]. Spectroscopy and Spectral Analysis, 2009, 29(2): 565-569.
[12] Miller R W, Chang C B. A Modified Cramer-Rao Bound and its Application[J]. IEEE Transactions on Information Theory, 1978, 5(24): 398-400.
[13] 徐本连, 王执铨. 一种新传感器组网策略在纯方位目标跟踪中的应用[J]. 宇航学报, 2006, 27(3): 379-384.Xu Ben-lian, Wang Zhi-quan. An Application of a New Strategy of Sensor Network to the Bearings-Only Target Tracking[J]. Journal of Astronautics, 2006, 27(3): 379-384.
Multi-optical Buoys Joint Localization Algorithm and Simulation
GUO Jian-zhong1, SUN Jian2, WANG Kai-shuai2
(1. Management Center of Navy Important Equipment, Beijing 100161, China; 2. System Engineering Research Institute, Beijing 100094, China)
To solve the problem that single or double optical buoys cannot obtain all-elements information of a target, based on the technique of calculating the moving elements of acoustic target, an algorithm for multi-optical buoys joint localization is presented in this paper. A mathematical model is established for the observation of optical buoys including positioning error, observation time error, and optical observation blur error. Utilizing the Monte-Carlo simulation method, the localization accuracy index of different number of optical buoys for maneuvering target considering all the above-mentioned errors is provided, and the effect of each factor on the joint localization of multi-optical buoys is analyzed simultaneously. The research provides data support for the engineering application of optical buoy.
optical buoy; maneuvering target; localization accuracy
TJ630.34; P715.2
A
2096-3920(2021)02-0176-07
10.11993/j.issn.2096-3920.2021.02.007
郭建忠, 孙健, 王凯帅. 一种多光学浮标联合定位算法及仿真[J]. 水下无人系统学报, 2021, 29(2): 176-182.
2020-09-03;
2020-11-02.
郭建忠(1979-), 男, 工程师, 硕士, 主要研究方向为系统工程.
(责任编辑: 许 妍)

