基于综合权重和物元可拓模型的城市道路运行状态评价

戴学臻,龙怡昕,周亚男,刘青云

(1.长安大学 运输工程学院，陕西 西安 710064; 2.南京市城市与交通规划设计研究院股份有限公司，江苏 南京 210008)

0 引言

随着社会经济的发展，小汽车保有量逐年在增加[1]，城市道路拥挤的现象也越来越明显，从而导致城市道路服务水平的下降，严重影响人们的出行。因此，科学、合理的对城市道路运行状况进行评价，可为城市道路提供规划的相关依据。

国内外学者对城市道路运行状况评价模型的研究和应用很广泛，如模糊综合评价法[2-4]、聚类分析法[5]、神经网络模型[6-7]、统计分析法[8-9]、指标评价法[10-11]等，这些方法可以取得一定的成效，但存在一定的缺陷。如统计分析法只能反映数据本身的规律，不能表现出数据的内在联系；指标评价法利用多个指标判断道路运行状态，然而忽略了指标之间的内在关联；模糊综合评价法偏向于最高和最低两极状态的研究，仅考虑了两级状态的隶属程度；聚类分析法在构建数学函数过程中，容易受到主观因素影响，导致评价结果不准确。

与其他城市道路运行状况评价方法相比，物元可拓评价方法通过物元理论确定经典域物元、节域物元、待评物元以及关联数，利用物元的可拓性进行定性分析，同时借助关联函数进行定量计算，定量化的表示评价结果[12]。其次可以将评价交通状态指标的不相容问题通过系统物元变换和结构变换方式，转换成相容问题[13-16]，从而实现多目标与单目标的转换，为城市道路交通状态评价提供新思路。

1 建立指标体系

根据《城市交通运行状况评价规范》[17]道路交通运行状态评价指标可以划分为基础性指标和特征性指标，其中基础性指标是以交通流3要素为基础，主要包括平均交通流量、自由流速度、平均行程速度。交通特征性指标是通过基础性指标扩展出来的，通过道路交通流数据和道路路段特征(如路段通行能力、路段长度)相结合，按照一定的准则所能表现出来的道路特征。交通特征性指标主要包括路段的饱和度、平均行程时间比、延误时间比、拥堵里程比等。

其中饱和度(V/C)可以反映道路交通流相对于道路通行能力的供需状况；延误时间比与路段的交通密度有关，可以从时间上反映道路的延误状态和车辆的相对行驶效率；平均行程速度可以表现路段所有车辆的运行速度。因此研究以饱和度、延误时间比(DTP)、平均行程车速作为评价指标。具体指标如下式所示：

(1)饱和度(V/C)等于某一路段的实际流率与道路通行能力之比，可以反映道路交通供需状态：

(1)

式中，S为道路饱和度；V为实际交通量；C为道路通行能力。

(2)延误时间比(DTP)：

(2)

(3)平均行程车速:

(3)

式中，vkj为时间间隔k内路段j的平均行程速度；Lkji为时间间隔k内第i辆车在路段j上行驶的距离；tkji为在时间间隔k内第i辆车在路段j的行程时间；n为观测行程时间的车次数。

本研究从基础性指标和特征性指标2个方面选取有代表性的3个指标，构建城市道路交通运行状况评价指标体系，如图1所示。

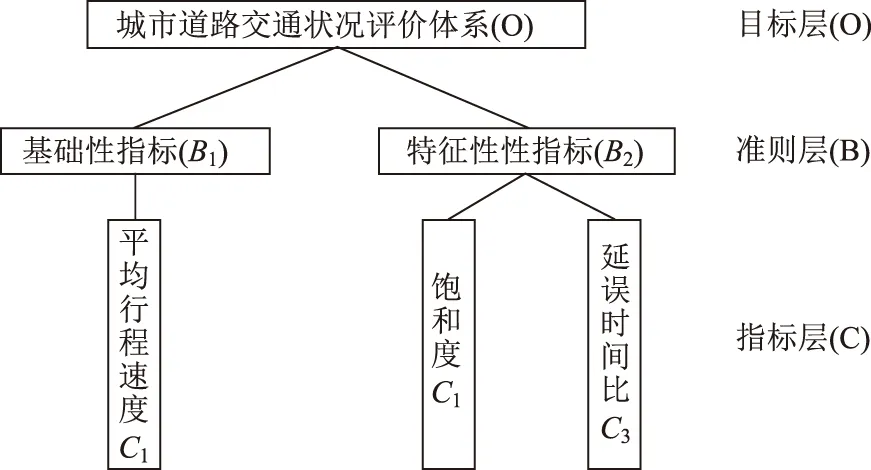
图1 城市道路交通运行状况评价体系模型Fig.1 Urban road traffic operation status evaluation model

参照《城市交通运行状况评价规范》[17]，将车辆平均行程车速、延误时间比和饱和度作为交通运行状况的3个评价指标，各评价指标标准如表1所示。

表1 城市道路交通运行状态评价标准

2 建立物元可拓模型

设Qj是城市交通运行状况第j个评价等级，Ci是第i个评价指标，Vi是第i个评价指标的值，则构成物元R=[Q,C,V]。

2.1 构建物元可拓评价模型的经典域物元

物元可拓评价模型的经典域物元矩阵Rj，可以表示为：

(4)

式中，Qj(j=1,2,3,4,5)为评价等级；Ci(i=1,2,3,…,n)为评价指标；vji(aji,bji)为评价指标Ci在评价等级Qj所对应的阈值范围，即构成物元可拓评价模型的经典域。

2.2 构建物元可拓评价模型的节域物元

节域物元矩阵Rp，可以表示为：

(5)

式中，Rp为评价等级的全体；vpi为Ci所取的量值范围，即指城市交通的节域。

2.3 确定待评物元

待评物元Ml(l=1,2,3,…,m)的物元矩阵RMl可以表示为：

(6)

式中，vli表示第l时间内Ml关于评价指标Ci的实际值，即待评时间间隔内评价指标的具体数值。

2.4 计算指标等级关联度

物元可拓评价过程的关键是确定关联度，关联度反映了各评价指标与各评价等级之间的联系程度。根据可拓理论中的中距定义，选取初等关联函数计算关联度Kj(vi)，计算公式为：

(7)

式中，Kj(vi)为vi的联系函数；vi为待评物元在各评价指标Ci下对应的实际量值；vji为经典域中各评价指标Ci下对应的阈值范围(aji,bji)，|vji|=|aji-bji|。

为了使关联度能进行分析和比较，将计算得到的关联度Kj(vi)根据公式(8)进行规范化处理，得到关联度Kji：

(8)

2.5 确定权重

在城市道路运行状态评价过程中指标权重的确定方法可按照计算方式的不同分为主观权重法和客观权重法。主观权重法通过专家主观经验及判断对影响道路的指标进行权重赋值，这类方法存在的缺点是绝对主观，缺乏对客观数据的分析，如层次分析法、三角模糊数法等；客观权重法通过采集到的数据对道路指标进行客观分析并赋予权重，这类方法的缺点是绝对客观，缺少主观经验值，如熵权法、相关系数法等。因此，研究将主观经验和基于客观数据的权重计算方法相结合，从而使指标权重与实际程度相符合，提高评价的准确性。本研究将三角模糊数法和熵权法与物元可拓评价模型结合，利用三角模糊数法经专家给出各评价指标分数进而确定主观权重，利用熵权法经各评价指标对应的数据进行计算进而确定客观权重，由二者确定评价指标的综合权重，进而采用物元可拓评价模型对城市交通运行状况进行定量评价，从而科学合理的确定城市道路的运行状况。

(1)基于三角模糊数确定权重

①专家评分。设第i个专家对第j个评价指标给出的评价分数为rij=[aij,bij,cij] (i=1,2,…,n;j=1,2,…,m)。aij为第i个专家对评价指标j影响程度给出的最保守分数；bij为第i个专家对指标j影响程度给出的最可能分数；cij为第i个专家对指标j影响程度给出的最乐观分数。

② 确定专家评价的权重集E=[e1,e2,e3,…,en]，en为第n个专家给出的分数值在综合分数中所站的比例。

③ 设模糊合成矩阵T=[a1,b1,c1],[a2,b2,c2],…,[am,bm,cm]；tj为合成矩阵T的第j项。

tj=ej。rj=[aj,bj,cj](j=1, 2, 3,…,m),

(9)

式中，aj为评价指标j最保守的分数值；bj为评价指标j最可能的分数值；cj为评价指标j最乐观的分数值。“。”为模糊合成算子，研究采用加权平均型算子M(⊗,⊕)进行模糊合成，这主要是因为加权平均型算子具有对多种因素的考虑，权数的体现以及评价矩阵信息的表现等多方面的优势[18]。

④确定三角模糊数权重。第j个评价指标的模糊得分为：

v″j=(aj+2bj+cj)/4,j=1, 2, 3,…,m。

(10)

设评价指标三角模糊集a=[a1,a2,a3,…,am]T，通过归一化处理得到第j个指标模糊数权重：

(11)

(2)基于熵权法确定权重

① 对原始评价矩阵X=(vli)m×n进行标准化处理，设yli为对各评价值vli标准化后的结果，计算公式为：

(12)

② 计算评价指标Ci的熵值ei，计算公式为：

(13)

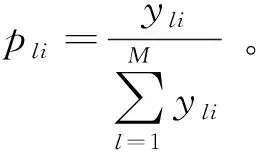
(14)

即b1,b2,b3,…,bn分别为C1,C2,C3,…,CN的权重。

(3)确定综合权重

设综合权重为w，为使综合权重wi与ai和bi尽可能接近，依据最小鉴别信息原理[19]，建立目标函数：

(15)

采用Lagrange乘子法求解上述问题，可得

(16)

根据式(16)计算评价对象各指标的综合权重。

2.6 判断评价等级

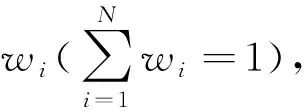
(17)

式中，Kj(RM)为待评路段RM符合评价等级Nj的隶属程度。取Kj(RM)=max{Kj(RM)}， 则待评物元属于等级j。

3 实例分析

选择陕西省西安市南二环路东段长安中路与雁塔北路之间路段为评价对象，设有3个调查站点，其中雁塔北路立交为路段起点设为调查站点1，长安路立交路段终点设为调查站点3，两个调查点之间利用摄影法记录来往车辆的牌照及通过时刻，调查点1与调查点3之间的距离为1.3 km；在长安大学彩虹桥上设置调查站点2，调查站点设置如图2所示。

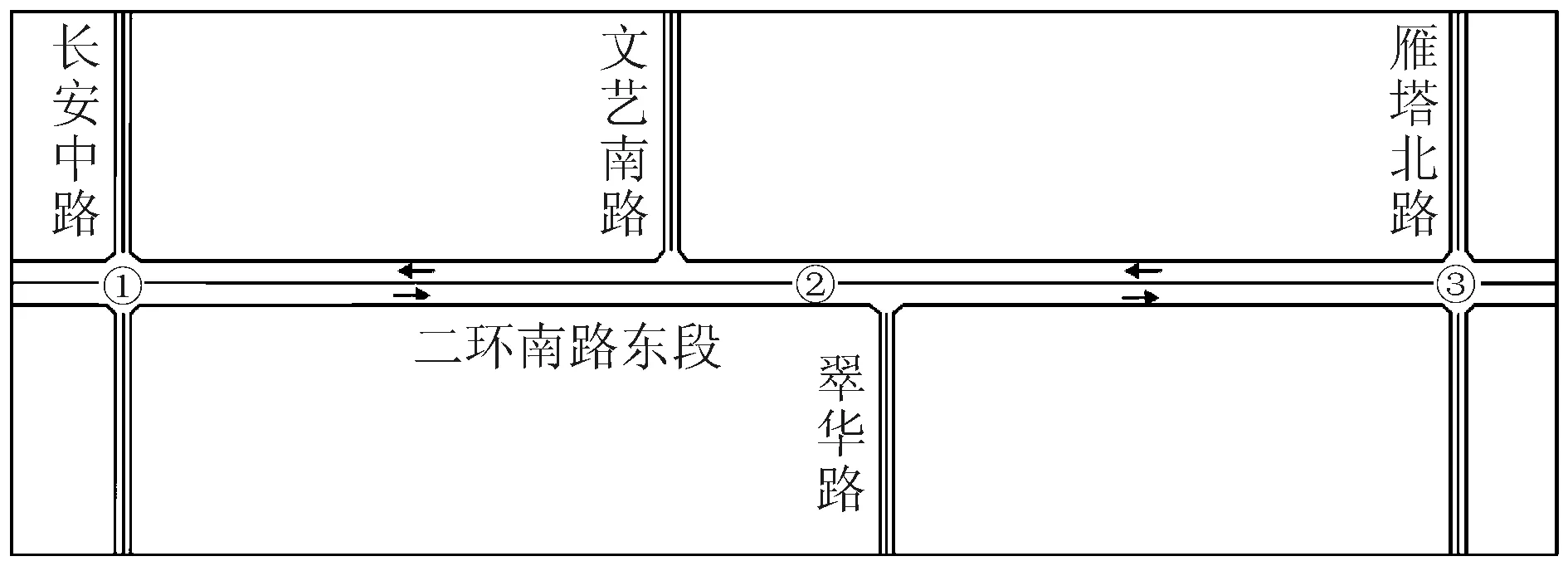
图2 调查站点示意图Fig.2 Schematic diagram of survey site

在2019年1月21日(周一)16:30—17:30对该路段交通状况进行调查，通过记录调查站点1和调查站点3的车辆牌照，以5 min为一个时间间隔，从16:30—19:30划分为36个时间段，计算该路段在每个5 min内的平均行程车速，每个时间段的平均行程车速(V)如表2所示。

表2 各时刻平均行程车速

以经过调查点2的每个5 min的饱和流量计算该时刻路段饱和度，饱和度如图3所示。

3.1 构建模型

城市交通运行状况评价等级Q，评价指标C和其具体值v共同构成城市交通运行状况物元。根据表2、表3和图3中数据构造1,2,3,4,5级分级标准的经典域矩阵RQ和节域矩阵RP：

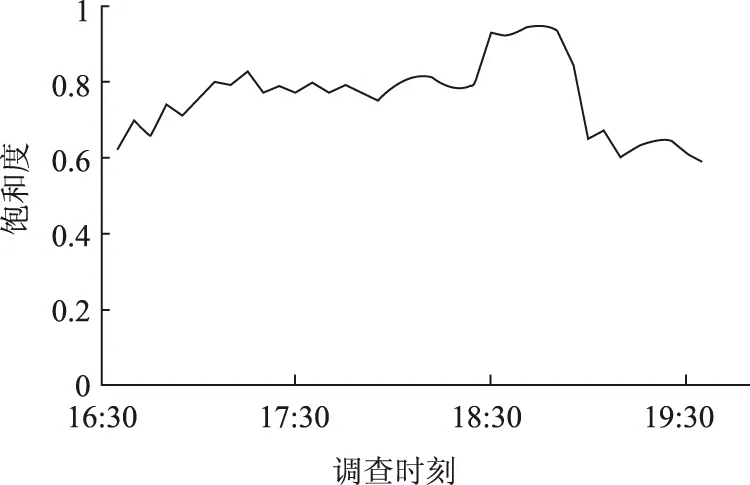
图3 路段内饱和度变化Fig.3 Variation of saturation in road section

表3 各时刻车辆延误时间比

以第一个时间间隔为例，构造待评物元矩阵R1，共36个待评物元矩阵。

3.2 计算关联度值

根据式(7)，利用matlab计算关联度Kj(vi)，并根据式(8)规范化关联度Kj(vi)，得到规范化关联度Kji，所得结果如表4所示。

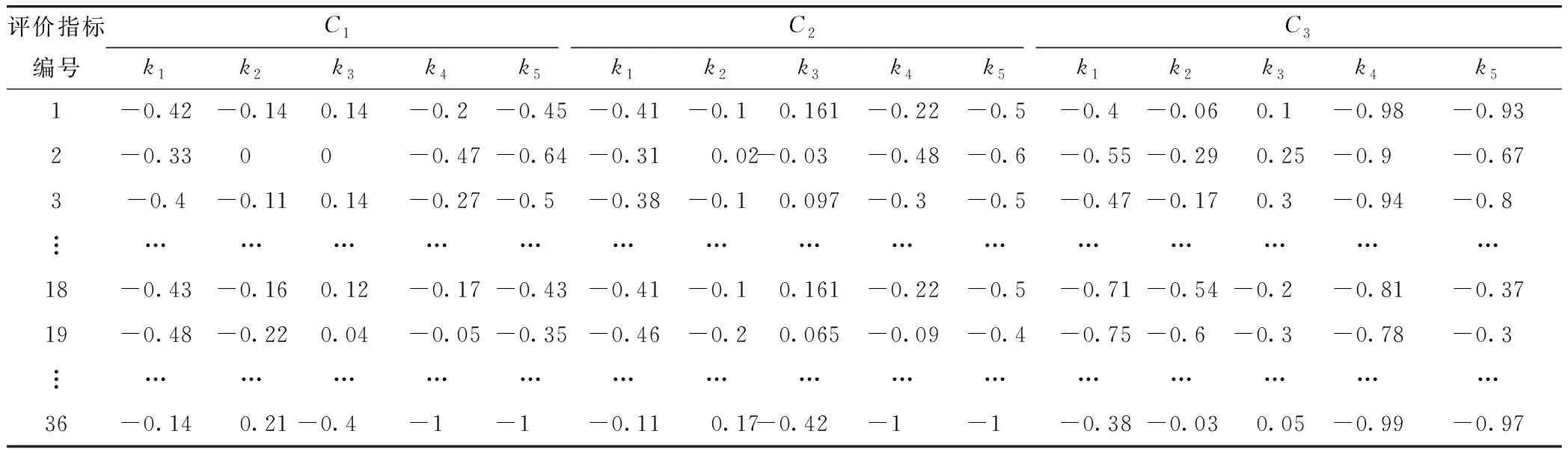
表4 各指标对应的各等级关联度值

3.3 确定综合权重

(1)三角模糊数法计算权重

基于城市交通运行状况评价指标，首先，选择3位专家参加本研究的评分，由专家给出各评价指标的最保守分数值、最可能分数值和最乐观分数值；3位专家给出C1分数值分别为[61,72,90]，[73,80,95]和[69,85,93]；C2分数值分别为[63,70,88]，[65,76,90]和[68,80,95]；C3分数值分别为[70,82,92]，[68,79,89]和[70,85,95]。其次，根据各专家给出的分数值在综合分数中所站的比例确定权重集E=[0.29,0.37,0.34]。最后将各专家对各评价指标的分数值和权重集代入式(9)～式(11)得到各指标的三角模糊数权重为：aj=[0.332 036,0.32 1678,0.346 287]。

(2)熵权法计算权重

根据熵权法式(12)～式(14)计算得到权重：bj=[0.326 018,0.336 334,0.337 648]。

(3)确定综合权重

将aj，bj代入式(16)，计算得到综合权重wj=[0.329 054,0.328 964,0.341 982]。

3.4 判断评价等级

将计算得到的综合权重代入式(17)，计算出待评路段关于平均行程速度、延误时间比和饱和度的加权关联度，取各等级中最大的关联度数值，最终得到各时间段对于等级j的关联度数值Kj(RM)，如表5所示。

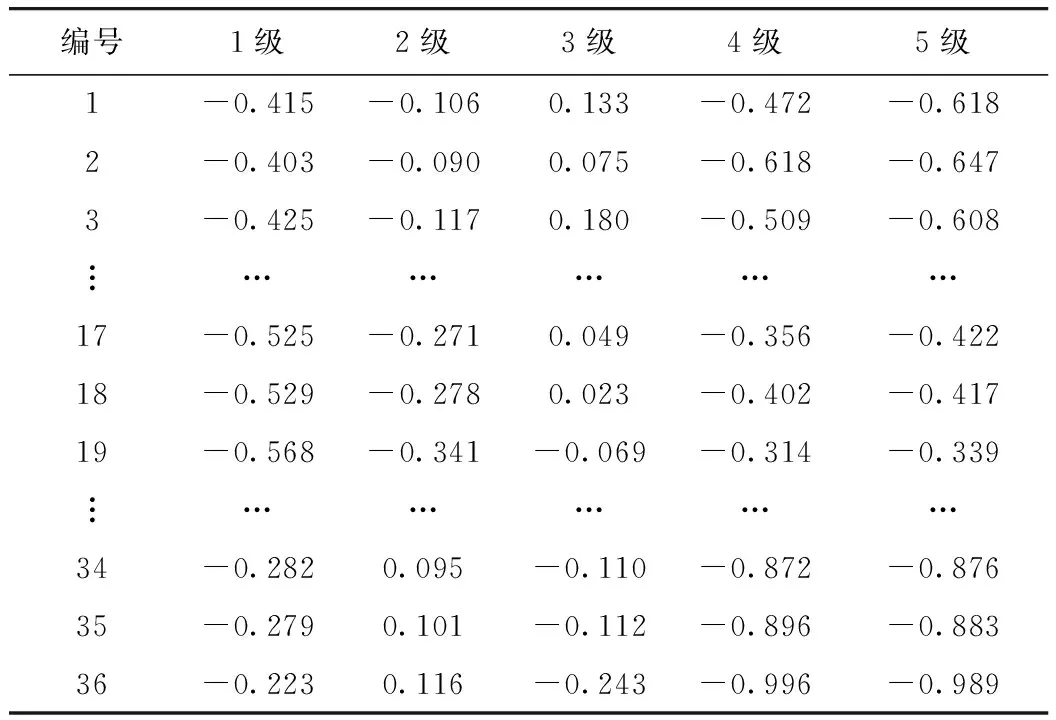
表5 各等级关联度数值

表中编号表示评价各时间段，1级表示交通状态与一级服务水平的关联程度；2级表示交通状态与二级服务水平的联系程…，表中数字表示各时间编号对各等级的关联度数值。

根据表6，基于物元可拓评价方法计算出的联系度值能够更直观地反映出与评价区间的贴近程度，如在时间段1时，各等级的联系度值中，3级的联系度值最高，说明此时车辆的运行状态最贴近3级，路段的运行状况较好。其次，物元可拓方法通过系统物元变换和结构变换，将平均行程运行速度、饱和度和延误时间比3个指标的不相容问题转换成相容问题，不再依赖单一指标确定道路状态等级，该方法最终以联系度值反映出道路状态等级，从而使得评价过程更加准确。

各时间段内交通状态对各等级关联度值变化状况图如图4所示：

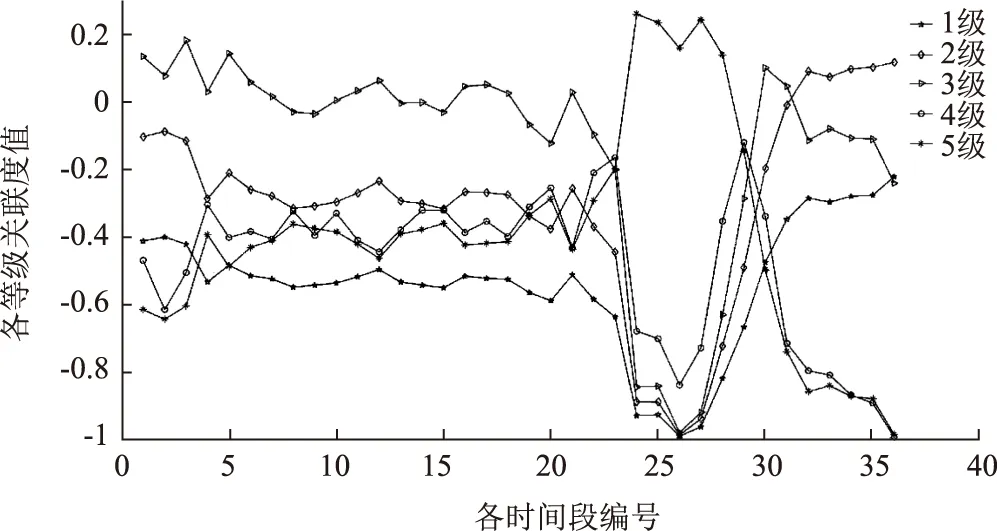
图4 各时间段内交通状态对各等级关联度的变化Fig.4 Change of correlation of traffic state to each level in each time period

根据图4，基于组合权重的城市交通运行状况物元可拓评价模型可以分析得到：首先在0—23时间段内，该路段3级服务水平为主，路段的运行状况较好，此时间段内路段比较畅通，但此时车辆有一定的延误；23—29时间段内，路段服务水平由3级骤降为5级，该路段在这个时间段内运行状况差，此时路段出现严重拥堵；30—32时间段内，路段服务水平由5级逐渐上升为3级，拥挤路段逐渐消散，车辆运行状况也逐渐趋于稳定；32—36时间段内，路段服务水平恢复为2级，路段交通状况趋于畅通。

根据表4，取1—36时间段中关联度数值最大的值，得到各个时间段与各等级的联系程度，判断出各时间段的拥挤等级。为了进一步对该方法的评价结果进行对比分析，研究采用模糊综合评价法对道路交通运行状态进行评价，采用最大隶属度原则计算得到各时间段的评价等级，如表6所示。

根据表6可以看出，模糊综合评价法和物元可拓评价法结果的趋势基本相同。在时间20和时间22出现模糊等级大于评价等级的情况，这是因为模糊综合评价法根据最大隶属度原则只能判断出该指标值属于某个评价区间，而不能判断出指标值对评价区间临界值的贴近程度；基于物元可拓方法能反映出与评价区间临界值的贴近程度。因此，基于双重权重的物元可拓评价模型能够准确、有效地反映道路各时间段内的运行状况。

4 结论

(1)针对城市道路运行状态判别，本研究从基础性指标和特征性指标两个方面构建了城市道路运行状况评价指标体系，并根据三角模糊数法和熵权法计算了各评价指标的综合权重，提出了基于综合权重和物元可拓模型的城市道路运行状态评价。

(2)基于综合权重和物元可拓模型的城市道路运行状况评价克服了指标权重绝对主观性和绝对客观性的缺陷，从而使指标权重与实际程度相符合，提高评价的准确性。

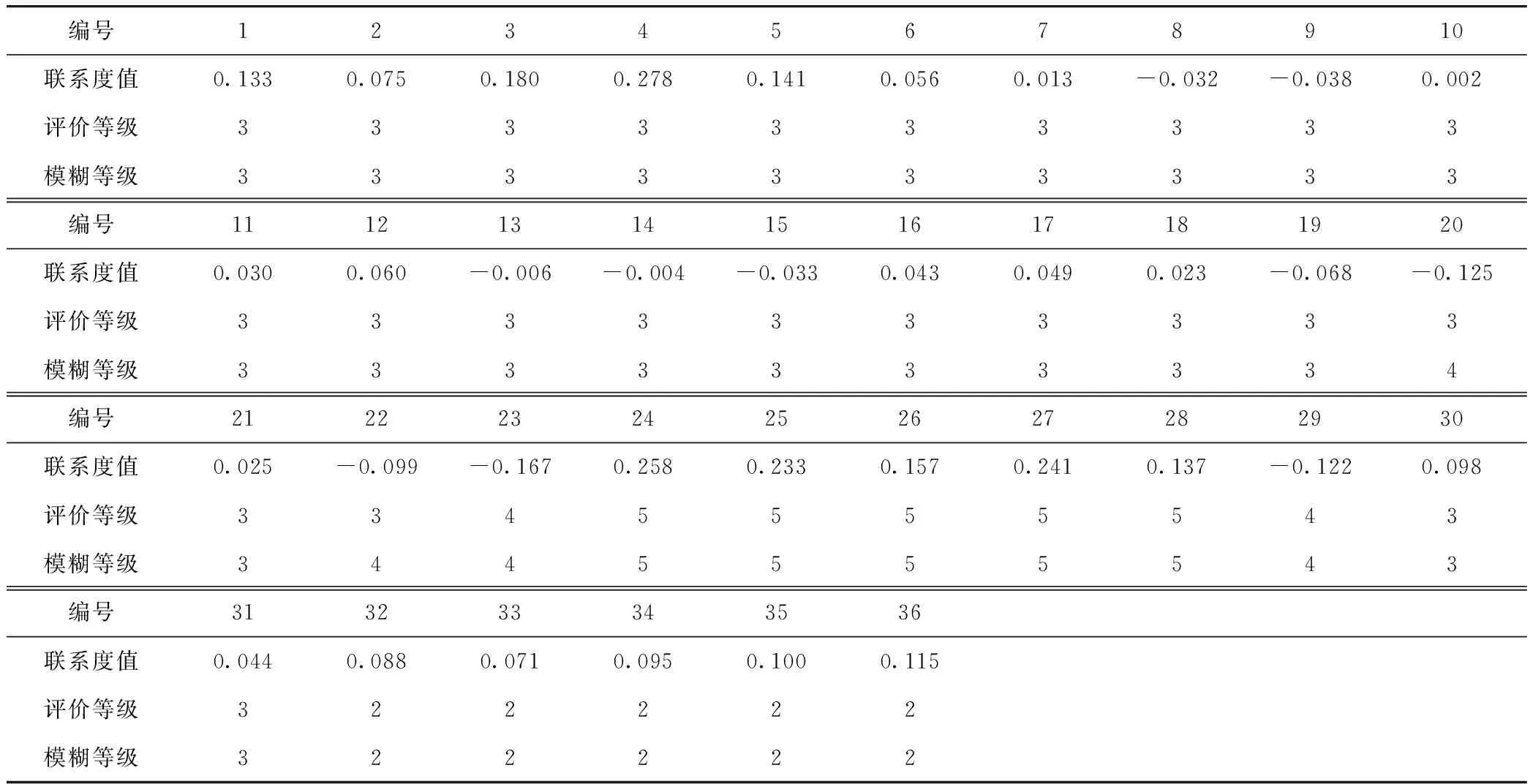
表6 各时间段联系度

(3)物元可拓模型考虑了各指标与各等级之间的联系程度、指标之间的不相容问题以及各关联度值与干扰评价区间临界值的贴近度。

(4)以西安市南二环路东段长安中路与雁塔北路之间路段的实测数据为例，通过与模糊综合评价法对道路交通运行状态进行评价，验证了基于双重权重的物元可拓评价模型能够准确、有效地反映道路各时间段内的运行状况。