随机激励下Frenkel-Kontorova 模型的纳米摩擦现象*
李毅伟 雷佑铭 杨勇歌
1) (山西农业大学数学系, 晋中 030801)
2) (西北工业大学应用数学系, 西安 710129)
3) (广东工业大学应用数学学院, 广州 510520)
基于一维Frenkel-Kontorova (FK)模型, 借助随机龙格库塔方法, 在非公度(incommensurate)和公度(commensurate)两种情形下, 分别研究了高斯白噪声激励下, 随机FK 模型的纳米摩擦现象(滞回和超滑)随噪声强度的变化而变化的规律.两种情形表明随着噪声强度的增大, 对减小系统滞回, 产生超滑有积极的影响.另一方面, 当系统机动性能(chain mobility)未达到饱和状态(B = 1)时, 噪声的引入, 能加速原子的运动, 使得原子更易脱离基底势的束缚而做运动, 但是当系统达到饱和状态后, 系统机动性能并不受噪声的影响.另外, 两种情形的区别是, 公度情形下, 由于原子受到基底势更强烈的耦合作用, 所以噪声对公度情形影响更为明显.
1 引 言
近年来, 随着精密机械和高科技设备的迅速发展[1], 特别是纳米科技所推动的新兴学科, 如纳米电子学、微型机械的发展, 都要求开展纳米摩擦学研究.由于这些领域使用的机械设备中, 摩擦副间隙或润滑厚度通常处于纳米范围, 此时宏观摩擦学不再适用, 其间的摩擦磨损与润滑性能必须从原子、分子的相互作用来考察.纳米摩擦学旨在研究纳米尺度上接触界面的摩擦行为和润滑机理, 从而建立材料微观尺度和宏观特性之间的关系.另外,摩擦问题对于微型设备仪器而言显得十分突出和重要.在某些方面, 摩擦作为阻力, 对于微型机械而言应减小其耗能, 尽可能达到零摩擦状态[1].因此纳米摩擦学迅速成为纳米科学技术研究的前沿和热点.另外, 随着纳米摩擦测试技术的进步和集群计算能力的提高, 推动了人们用简单的数学模型来探索复杂体系的纳米摩擦机制, 而Frenkel-Kontorova (FK)[2]模型便是成功地描述和解释有关复杂摩擦体系的动力学模型之一.许多学者借助经典的FK 模型研究纳米摩擦学的一些现象[3−27].如今, 它已经成为了研究纳米摩擦学领域的一种重要的理论工具.通过对FK 模型的研究[12−14], 成功地描述和解释了滞回、超滑等现象的产生诱因.这些结论很好地解释了纳米摩擦领域的一些问题, 成功地将FK 模型和纳米摩擦联系起来.
迄今为止关于FK 模型的研究主要集中在确定性情形[5−14], 然而真实的系统往往受到随机因素的影响[4], 微纳观系统更是如此.Guerra 等[24]分别从不同角度研究了温度的变化对系统纳米摩擦现象的影响, 表明温度对系统减小滞回有积极影响;Tekić等[15−18]也从夏皮洛台阶(Shapiro step)等角度探讨了噪声激励下的FK 模型.目前关于随机FK 模型的研究仍然处于探索阶段, 因此考虑随机FK 模型的研究对于理解纳米摩擦机理更具有实际意义.本文主要研究高斯白噪声激励下的FK模型的一些纳米摩擦现象(如滞回、超滑等现象)的变化规律.通过改变噪声强度, 刻画噪声强度与滞回、超滑等现象之间的定量关系[8].通过研究高斯白噪声激励下的FK 模型对研究其他随机激励下的FK 模型具有借鉴意义.也对进一步建立适用于随机FK 模型的新的分析方法提供依据.
2 理论模型
基于确定性的一维FK 模型[12−14], 本文进一步考虑高斯白噪声激励下由N个原子构成的随机FK 模型, 模型中第i( 1 ≤i≤N) 个原子满足如下运动方程:
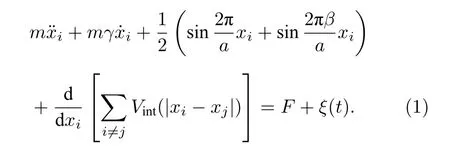
不失一般性, 本文采用无量纲化处理, 假设每个原子的质量m=1.xi表示第i个原子的位置( 1 ≤i≤n,1 ≤j≤n).系统的阻尼项用表示[8,12], 外势周期为a, 当参数β=89/144[12], 表示非公度情形下准周期基底(quasiperiodic substrates), 当参数β=24/30 , 表示公度情形下多势阱周期基底(multiple-well periodic substrates).[26]表示其他原子对第i个原子的作用势, 即对所有的j求和.本文原子间的作用势采用Morse 势:其中K表示弹性系数.基底势由晶格常数(原子链处于平衡状态时相邻原子间的距离)为b=L/N(L为链长), 外势周期a和c=a/β共同决定[12,24].则与Morse 势相关的原子间的作用力Fint(x) 可表示为
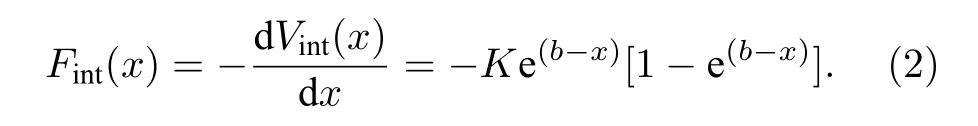
(1)式右端,F表示维持原子链运动的无量纲外力;高斯白噪声ξ(t) 与系统阻尼项之间满足涨落耗散理论[24]:
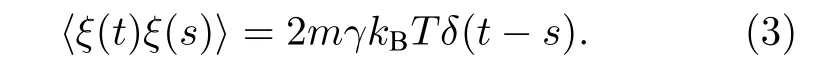
这里kB为玻尔兹曼常数,T为环境温度.为简化说明, 令D=mγkBT, 则(1)式中的高斯白噪声满足统 计 性 质[28]:〈ξ(t)〉=0和〈ξ(t)ξ(s)〉=2Dδ(t −s) ,D代表噪声强度.为处理(1)式中的高斯白噪声,采用针对白噪声的随机龙格-库塔法[28]进行模拟.
在数值模拟过程中采用周期性边界条件[8,12,24]:xi+N=xi+Nb.通过引入新的变量vi,ui将(1)式进行降阶处理, 得到如下随机微分方程组:
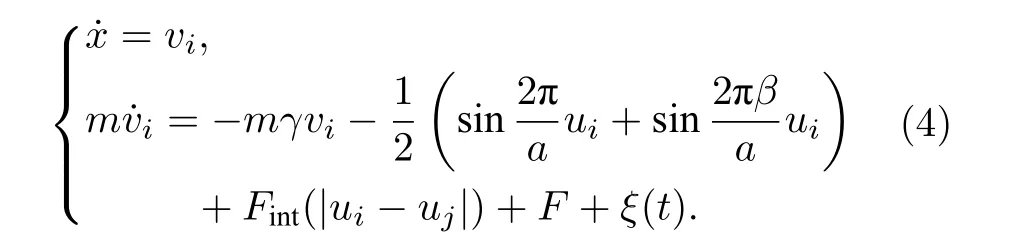
所有粒子在初始时刻处于静止分布.为避免其他因素干扰, 系统处于理想的绝热状态.记录原子链在稳定状态时的条件(速度和位移)作为下一时刻的初始条件.定义系统的平均速度:
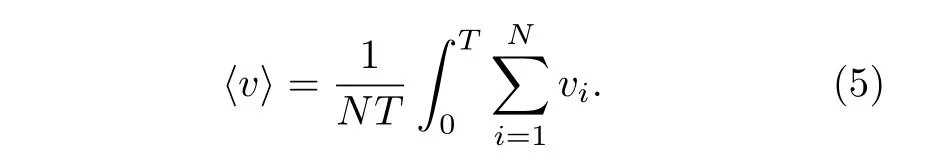
另外, 当外驱动力小于某个临界值时, 系统平均速度为零, 当外驱动力大于该临界值时, 系统的平均速度不为零, 在外驱动力的作用下系统发生相对运动, 称该临界值为最大静摩擦力Fs.Vanossi等[12]和Braun 等[13]有关FK 模型的研究表明, 当弹性系数K较小, 且系统处于欠阻尼状态时, 系统的滞回现象明显, 也便于本文有关问题解释说明.因此, 如未强调,K=1 ,γ=0.7.为了研究系统的运动性能, 类似于文献, 引入指标B=VCM/F[24]刻画原子链的机动性能(chain mobility),VCM表示原子链质心(center of mass)的平均速度.Bf=(mγ)−1表示原子链移动的最大渐进值[24].
由于晶格常数b和外势周期a这两个长度标度相竞争[2], 使得基态结构非常复杂.当b/a=1 ,称为公度.当b/a=144/233 , 称为黄金分割.当b/a=351/256, 称为螺旋分割.黄金分割和螺旋分割属于非公度情形[8].对于非公度情形, 因为相邻原子间的距离不可通约, 系统内的所有原子容易脱离基底的束缚做同步运动; 而公度情形下, 原子要被束缚在基底势的势阱中, 所以系统本身在非公度和公度情形下有所区别[8,10].另外, 随着外力F绝热增加和减小的过程中, 系统发生了钉扎-脱钉(pinning-depinning)的转变过程, 在这个过程中,出现了滞回的有趣现象, 它源于原子间的相互作用.当外驱动力绝热增加时, 系统从锁定状态转变为运动状态, 出现脱钉转变; 当外驱动力绝热减少时, 系统从运动状态转变为锁定状态, 出现钉扎转变.并且发生脱钉和钉扎转变时的驱动力往往是不同的, 发生钉扎转变时的摩擦力小于发生脱钉转变时的摩擦力(存在滞回现象), 这表明发生脱钉转变和钉扎转变的机理是不同的[12,24].因此本文将分别从非公度情形(以黄金分割为例)和公度两种情形,研究外力驱动的FK 模型在随机激励下, 系统的纳米摩擦现象(滞回以及最大静摩擦力)随噪声强度的变化规律.
3 数值结果及其分析
3.1 非公度( b /a=144/233 )情形
图1 和图2 描述了在非公度情形下, 随着噪声强度D的增大, 系统机动性能B随着外力绝热增加和减小而改变的规律.此部分以黄金分割为例, 在数值模拟过程中, 取a=1,b/a=144/233 ,c=a/β=144/89[8,12], 此时链长L=144 , 原子个数N=233.
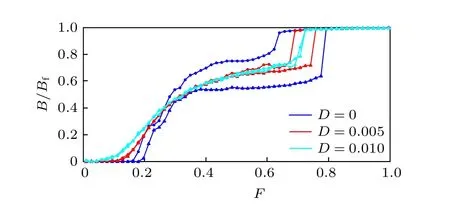
图1 D = 0, 0.005, 0.010 时, 非公度情形下系统机动性能B 随外力F 的改变的变化规律(图中三角形和原点分别表示外力F 绝热增加和减小的过程)Fig.1.Noise effects on static friction and hysteresis of the B(F)characteristics for the incommensurate case when D =0, 0.005, 0.010.Triangles and circles denote, respectively,the adiabatic increasing and decreasing process of F.
如图1 所示, 当噪声强度D=0 , 即为确定性FK 模型[8,12], 系统有明显的滞回现象.随着噪声强度D的增大, 系统的滞回区域的面积有明显减小的趋势, 与此同时最大静摩擦力Fs也随着噪声强度的增大有减小的趋势, 表明噪声使得原子更容易脱离基底的束缚, 做同步运动.
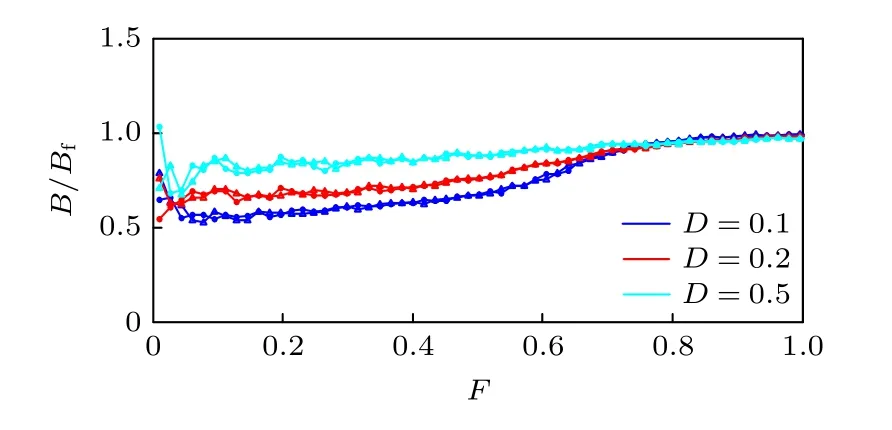
图2 D = 0.1, 0.2, 0.5 时, 非 公度情形下 系统机 动性能B 随外力F 的改变的变化规律Fig.2.Noise effects on static friction and hysteresis of the B(F)characteristics for the incommensurate case when D =0.1, 0.2, 0.5.
另外, 随着外力F增大的过程中, 噪声的引入会加速系统的运动(如当外力F=0.6 时, 噪声强度越大, 系统机动性能越大).进一步, 对于确定性系统(D=0 )时, 当外力F≈0.8 , 此后随着外力F的增大, 系统的机动性能B不再随外力的增大而改变, 达到饱和状态(称机动性能为B=1 为饱和状态).
随着噪声强度的增大, 加速了原子的运动, 使得系统的机动性能更早的达到饱和状态 (如当噪声强度D=0.005 , 外力F≈0.75 ; 当噪声强度D=0.01 , 外力F≈0.7 ), 此后系统的机动性能达到饱和状态, 不随噪声强度以及外力的增大而改变.此时, 随机激励下系统的机动性能与确定性系统下机动性能是一致的(B=1 ), 表明饱和状态下的机动性能是系统固有的属性.
随着噪声强度进一步增大, 如图2 所示, 系统滞回现象消失, 也产生了超滑现象.验证了噪声的引入对减小滞回, 减小系统摩擦, 产生超滑有积极的影响.另外, 随着噪声强度的增大, 系统的平均机动性能有明显增大的趋势, 更早地达到饱和状态(B=1 ), 但当系统达到饱和状态后(如当外力F≥0.8时), 系统的机动性能不受噪声的影响.进一步验证噪声使得原子更易脱离基底的束缚, 做同步运动, 但噪声并不改变系统的饱和状态下的机动性能.
图3 则从整体上考察了, 系统的最大静摩擦力Fs受噪声强度D影响的变化规律.也验证了图1和图2 的结论.结果表明, 随着噪声强度的增大,最大静摩擦力有减小的趋势, 当噪声强度D ≈0.1时, 系统将产生超滑现象.
综上, 由图1—3 可得, 在非公度情形下, 当系统的机动性能未到饱和状态时, 噪声的引入加速了原子脱离基底的束缚, 改变了系统的滞回区域的面积以及最大静摩擦力的大小, 噪声强度越大, 系统的机动性能越早地到达饱和状态.但当系统机动性能达到饱和状态后, 随着外力的改变, 噪声强度并不改变系统的机动性能.因此为减小摩擦, 产生超滑, 适度的噪声激励即可.
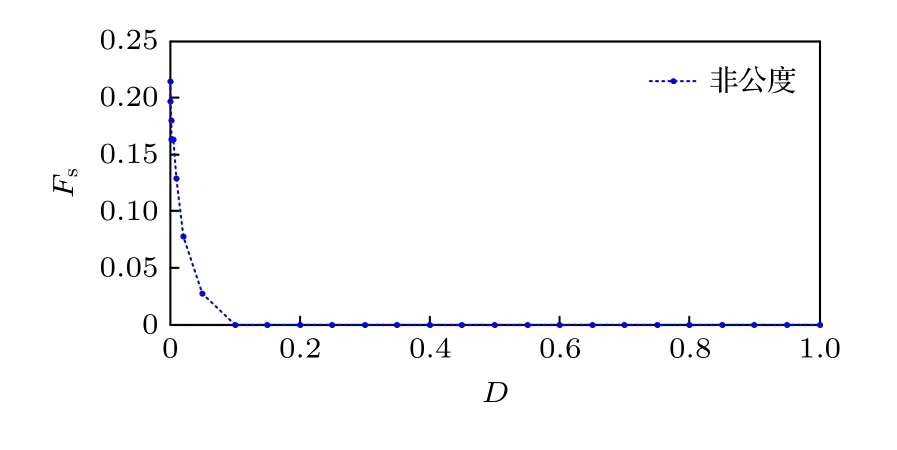
图3 非公度情形下最大静摩擦力 Fs 随噪声强度D 的改变的变化规律Fig.3.Noise effects on maximum static friction for the incommensurate case.
3.2 公度( b /a=1 )情形
为验证噪声对系统纳米摩擦现象的影响.此部分将在公度情形下, 研究随机因素影响下, 系统的纳米摩擦现象随着噪声强度的增大而变化的规律.其中a=1,c=a/β=30/24 , 此时, 链长L=140 ,原子个数N=140[8,12].图4 和图5 描述的是系统的机动性能B随着外力F绝热增大和减小而发生变化的过程.

图4 D = 0, 0.005, 0.010 时, 公度情形下系统机动性能B 随外力F 的改变的变化规律(图中三角形和原点分别表示外力F 绝热增加和减小的过程)Fig.4.Noise effects on static friction and hysteresis of the B(F)characteristics for the commensurate case when D =0, 0.005, 0.010.Triangles and circles denote, respectively,the adiabatic increasing and decreasing process of F.
如图4 所示, 当无随机激励(D=0 )时, 系统有明显的滞回现象, 随着噪声强度的增大, 滞回区域的面积有明显减小的趋势直至消失.此过程系统的最大静摩擦力Fs也随着噪声强度的增大而减小.印证了非公度的相关结论.
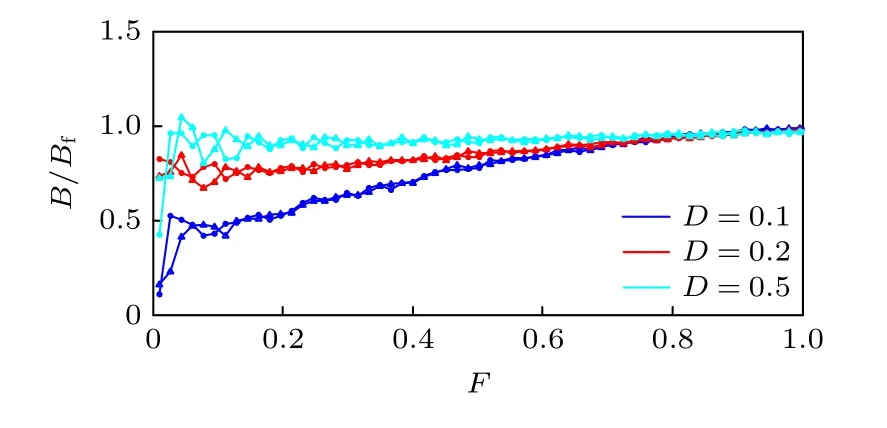
图5 D = 0.1, 0.2, 0.5 时公度情形下系统机动性能B 随外力F 的改变的变化规律Fig.5.Noise effects on static friction and hysteresis of the B(F)characteristics for the commensurate case when D =0.1, 0.2, 0.5.
另一方面, 当系统机动性能未达到饱和状态时, 随着外力F的增大, 噪声加速了原子的运动,使得系统的机动性能更早地达到饱和状态(D=0, F ≈0.93 ;D=0.005 ,F ≈0.90;D=0.01, F ≈0.79).之后, 系统的机动性能B不受外力以及随机因素的影响.
对比图1 和图4.非公度情形下, 链长L=144 ,
原子个数为N=233.公度情形下, 链长L=140 ,而原子个数为N=140.当链长相差不大的情况下,公度情形下, 原子个数相对较少, 但当噪声强度D=0时(此时为确定性FK 系统), 公度情形下的滞回区域却明显大于非公度情形下的滞回区域[12].公度情形下, 最大静摩擦力也大于非公度情形.与非公度相比(如图1 所示), 公度情形下, 系统滞回受随机因素的影响变化更为明显, 系统的最大静摩擦力改变也更为明显(如图6 所示).公度和非公度的区别在于: 公度情形下, 要移动原子链, 就必须使原子爬上并越过外势的顶部, 从而克服一个势垒[29].噪声的引入, 使得这种束缚变得极不稳定,此时原子也会逃离势阱做同步运动.因此, 公度情形下, 系统受到的耦合作用更为强烈.从而噪声对公度情形的影响也更为明显.
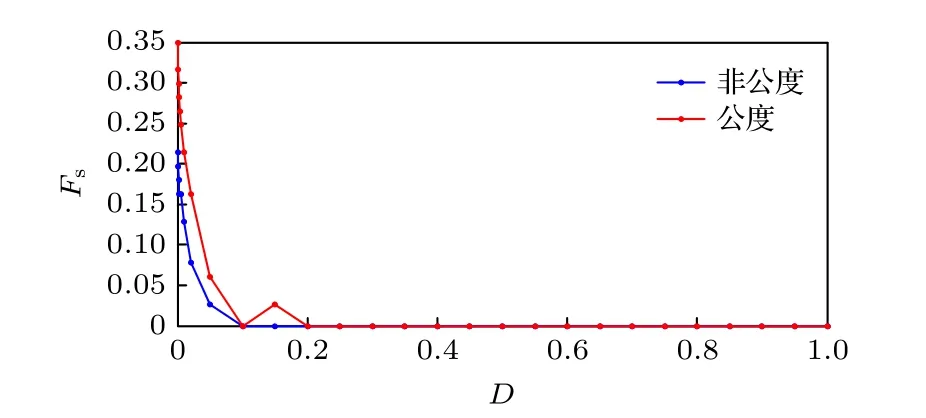
图6 公度与非公度情形下最大静摩擦力 Fs 随噪声强度D 的改变的变化规律Fig.6.Noise effects on maximum static friction for the incommensurate case (blue) and the commensurate case (red).
如图5 所示, 进一步增大噪声强度, 系统的滞回消失, 产生超滑现象.当外力F<0.8 时, 随着噪声强度的增大, 系统的机动性能B随着噪声强度的增大而增大, 表明噪声的引入, 使得原子更容易脱离基底势的束缚而运动.但当外力F≥0.8 , 系统的机动性能不受噪声强度以及外力的影响.验证了噪声容易使得原子脱离束缚, 但并不改变系统饱和状态时的机动性能.
进一步, 图6 从总体上描述了最大静摩擦力Fs随噪声强度D的改变的变化规律.在非公度和公度状态下, 随着噪声强度的增大, 最大静摩擦力都有减小的趋势, 当噪声强度D≈0.1 , 系统将产生超滑现象.不同之处在于, 由于公度情形下, 原子受到基底势更强的耦合作用, 所以噪声的引入, 使得这种束缚变得极不稳定, 此时原子也会逃离势阱做同步运动, 所以对公度情形下(如滞回, 最大静摩擦力)的影响更为明显.
4 结 论
本文从非公度和公度两方面, 研究了高斯白噪声激励下的一维随机FK 模型.讨论了系统纳米摩擦现象受噪声强度影响的变化规律.结果表明: 在非公度和公度情形下, 随着噪声强度的增大, 对减小系统的滞回和减小摩擦有积极影响, 当噪声强度选择恰当, 系统将产生超滑.另一方面, 噪声的引入, 加速原子运动, 使得系统更快地进入饱和状态,但当系统达到饱和状态后, 系统的机动性能并不受噪声的影响.因此, 为减小滞回, 产生超滑, 适当的噪声强度即可.
非公度和公度的区别在于: 受噪声影响, 公度情影响更为明显.表明相同前提下, 公度情形由于受到基底势更为强烈的耦合作用[8,29]从而具有更为复杂的动力学行为.通过对高斯白噪声激励下的FK 模型的研究, 对其他有色噪声激励下的FK 模型有更好的借鉴意义.对于人们设计出超润滑材料, 以及制造出具有工程应用价值的新材料有一定的借鉴作用.