基于非线性控制参数组合策略的灰狼优化算法
张孟健 龙道银 杨小柳 王 霄 杨 靖*
1(贵州大学电气工程学院 贵州 贵阳 550025) 2(中国电建集团贵州工程有限公司 贵州 贵阳 550001)
0 引 言
自20世纪90年代以来,群体智能优化算法因结构简单、易于实现和求解效率高等特点,被研究学者广泛地应用于复杂问题的求解及实际的优化问题中。其中较为典型的算法有遗传算法(Genetic Algorithm, GA)[1]、粒子群优化算法(Particle Swarm Optimization, PSO)[2]、蚁群算法(Ant Colony Optimization, ACO)[3]、差分进化(Differential Evolution, DE)算法[4]等。受灰狼群捕食行为的启发, 澳大利亚学者Mirjalili等[5]在2014年提出了一种新的群体智能化优化算法,即灰狼优化算法(Grey Wolf Optimizer,GWO)。
对于灰狼优化算法的改进研究中,文献[6-10]针对收敛因子a分别给出了不同的改进策略,使得a随迭代次数的增加呈非线性动态变化,从而有效地平衡算法的全局探索和局部开发的能力。文献[6]提出一种控制参数a随机动态调整的策略来达到动态自适应目的;文献[7]提出基于余弦函数和二次函数的非线性动态变化收敛因子更新方法;文献[8]提出一种基于指数变化的参数a的调整策略,并运用在二维平面的无线传感网络节点的优化部署中,但调节系数的选择没有详细叙述;文献[9]提出一种基于对数递减策略的非线性动态变化的收敛因子控制策略,并运用在基于测距的无线传感器网络定位中;文献[10]提出一种基于余弦函数的非线性控制参数策略,寻优效果相对较好,但需要进一步的改进研究;文献[11]提出一种基于混沌映射混合粒子群的GWO,收敛因子a采用了二次函数进行动态调整。
与其他群体智能算法类似,标准 GWO 也存在易陷入局部最优、后期收敛速度慢、求解精度不高等缺点。本文提出新的非线性控制参数策略与权值系数的非线性调整参数控制策略,并对多组基准测试函数进行仿真实验,对测试的结果进行分析来验证所提策略的有效性。
1 灰狼优化算法基本模型
GWO模拟了狼群的社会等级制度和群体的狩猎行为[5]。从数学角度设计GWO时,结合灰狼的实际社会等级,将最优解设为α狼;次优解设为β狼;第三优解设为δ狼;剩余的解归为ω狼。
灰狼群狩猎过程包括接近和包围猎物,其数学表达式[5]如下:
D=|C·XP(t)-X(t)|
(1)
X(t+1)=XP(t)-A·D
(2)
式中:D为个体与目标之间的距离;t为当前的迭代次数;C和A为系数向量;Xp为目标的位置向量;X为单只灰狼的位置向量。其中A和C的计算公式如下:
A=2a·r1-a
(3)
C=2r2
(4)
式中:r1、r2为[0,1]之间的随机数生成的向量;a为收敛因子,其值随迭代次数的增加从2线性递减至0。
a=2-2ti/tmax
(5)
式中:tmax为最大的迭代次数,其中i=1,2,…,N。
灰狼个体跟踪猎物位置的公式表述如下:
(6)
式中:Dα、Dβ、Dδ分别表示α、β和δ与其他个体之间的距离;Xα、Xβ、Xδ分别表示α、β和δ当前的位置;C1、C2、C3为系数随机向量;X为单只灰狼的当前位置向量。
在猎捕阶段中,剩余的ω狼个体向着α、β和δ狼的前进步长和方向,其表述如下:
(7)
其中灰狼个体位置的更新公式如下:
X(t+1)=(X1+X2+X3)/3
(8)
2 改进GWO
对于不同的控制参数策略及非线性控制参数的组合策略中的调整参数,选取多组值进行仿真实验,并通过多组实验的结果分析,选择最佳的组合策略的调整参数值。
2.1 非线性控制参数
文献[5]采用的是线性控制策略,可表示为:
a0(t)=afirst-afirst·(t/Tmax)
(9)
本文提出一种基于正弦函数的调整参数控制策略,公式如下:
(10)
式中:afirst、afinal分别为控制参数的初值和终值;μ和λ均为调节参数;Tmax为最大迭代次数。
此外,为了进行权值系数的调整参数控制策略研究,本文应用了文献[7-8]中收敛因子的迭代公式:
(11)
(12)
式中:γ为非线性调系数;k为算法开发和搜索能力影响因子,其值越小,则算法在最优解附近搜索新的最优解的能力越强。本文中γ=10,k=7。
2.2 改进的非线性控制参数策略
根据式(10)-式(12),选择a1、a2、a3三种策略进行组合,提出权值系数的调整参数控制策略,进而权衡局部搜索和全局搜索的收敛速度。表示如下:
(13)
则组合后的收敛因子可表示为:
a=ω1·a1+ω2·a2+ω3·a3
(14)
2.3 改进策略调节参数的设定
针对本文的非线性控制参数的组合策略,在μ=2时,给定不同的调节参数值及其随迭代次数的变化曲线如图1所示,其中控制参数a0、a1、a2、a3、a的5种策略分别为传统的灰狼优化算法(GWO)、组合策略的参数控制的灰狼优化算法(GWO1)、基于正弦函数的调整参数控制策略的灰狼优化算法(GWO-SIN)、文献[7]提出的二次函数控制参数的灰狼优化算法(GWO2)、文献[8]提出的指数控制参数的改进灰狼优化算法(GWO3)的仿真策略。本文分别对不同的λ和k的值进行仿真实验,其中λ的取值为2~5,k的取值为6和7,限于篇幅,本文只给出2个仿真图。
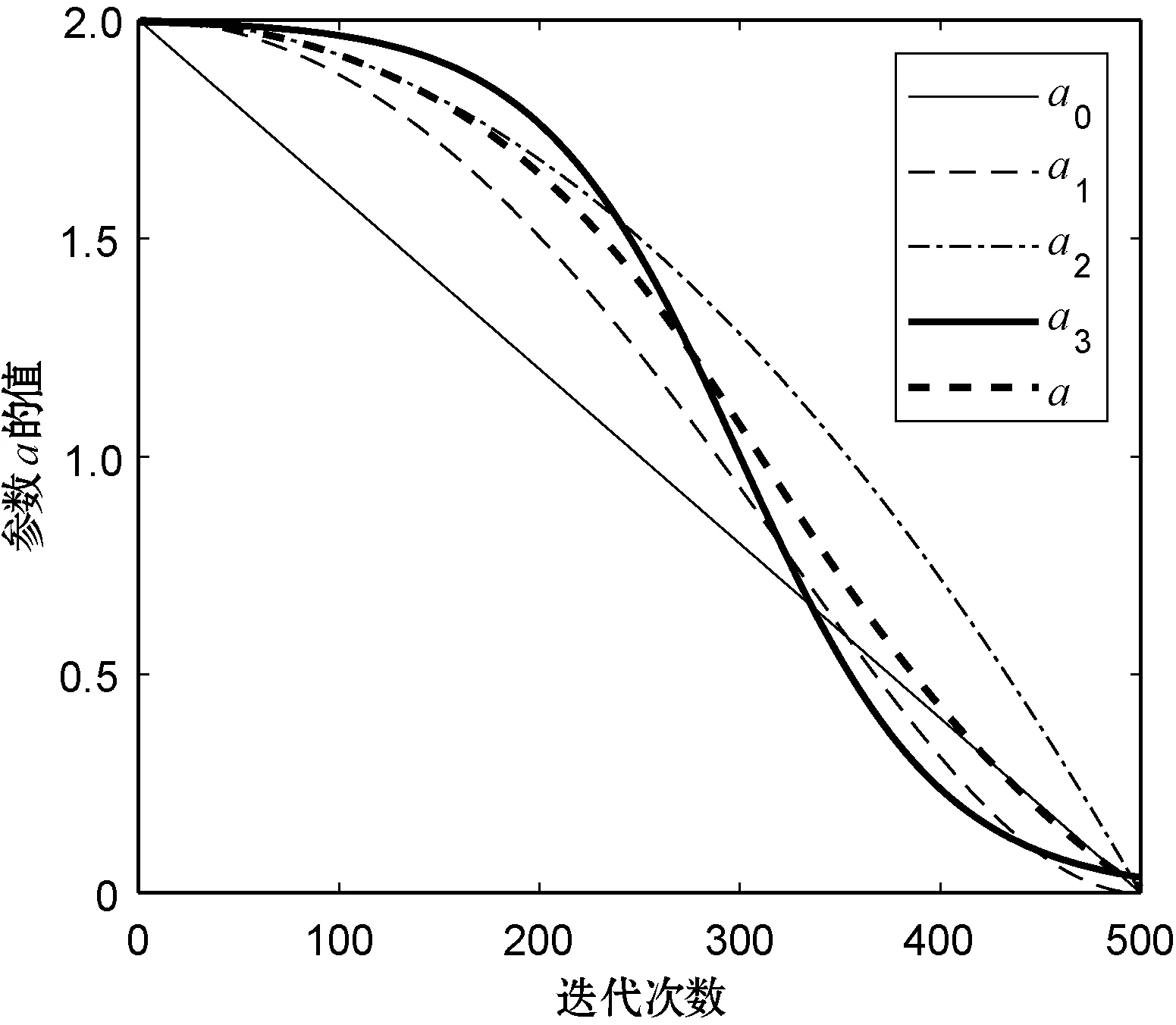
(a) λ=2,γ=10,k=6
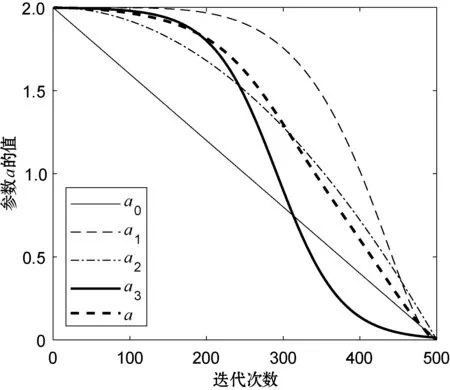
(b) λ=5,γ=10,k=7图1 不同权值动态因子随迭代次数的变化曲线
可以看出,控制参数a随迭代次数的曲线变化斜率对于非线性控制策略都是不断变化的,文献[7-8]提出的控制参数非线性的改进策略与本文提出的非线性参数控制调整策略均可有效地均衡算法的局部搜索和全局搜索能力。由式(3)可以知道,控制参数a是搜索参数A的一个重要的影响因素,直接影响算法的局部搜索和全局搜索能力。图1中的5条曲线分别对应不同的参数控制策略,对算法的收敛速度及求解结果有不同程度的影响。
此外,为了验证本文所设定的调节参数值的合理性,针对5种算法选择F1、F2、F4和F5等4个基准测试函数进行仿真测试,并根据实验结果选择最佳的调节参数值。仿真结果如表1-表3所示。
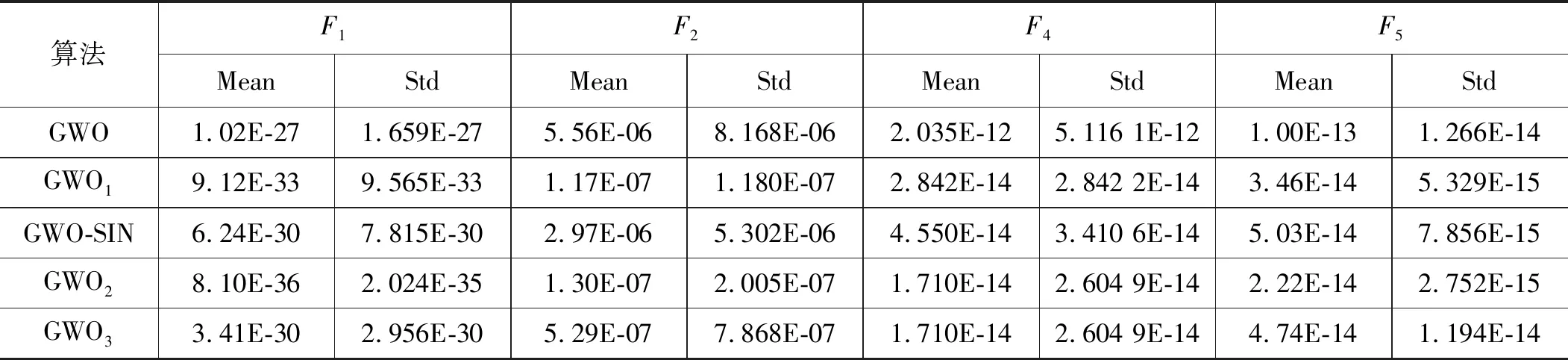
表1 参数λ=2、γ=2、k=6时对应的函数测试结果

表2 参数λ=5、γ=10、k=6时对应的函数测试结果

续表2

表3 参数λ=5、γ=12、k=7时对应的函数测试结果
为了保证参数选取实验的准确性,本文对选择的4个基准测试函数分别进行10次独立测试,并计算各组解的均值(Mean)与方差(Std)。分析结果如下:
从表1的函数测试结果来看,当调节参数μ=2,λ=2,非线性调系数γ=10,算法开发和搜索能力影响因子k=6时,GWO1对单峰函数F2的求解最佳,对于函数F1、F4、F5的测试结果,平方参数控制策略的GWO2的求解最佳。
从表2的函数测试结果来看,当μ=2、λ=5、γ=10、k=6,对于单峰函数及多峰函数F4,组合策略GWO1的求解均优于传统的GWO、GWO2、GWO3和GWO-SIN;对于多峰函数F5,组合策略GWO1的求解均优于传统的GWO、GWO2和GWO3,略劣于GWO-SIN。
从表3的函数测试结果来看,当μ=2、λ=5、γ=12、k=7时,除了对函数F2的求解,其余3个函数GWO-SIN的求解均为最佳。
比较表1-表3的测试结果,γ=12、k=7时GWO2对于单峰函数的求解要劣于γ=10、k=6时的值。
综合上述的分析,选择最佳的调节参数值,即μ=2、λ=5、γ=10、k=6。
2.4 搜索参数A的仿真分析
在迭代过程中,收敛因子a的值由2逐渐减小至0,A的范围随a的值减小而减小。当|A|≤1时,灰狼群收缩搜索范围向着猎物攻击,即实现局部搜索;当|A|>1时,灰狼群体扩大搜索范围远离猎物,以加强算法的探索能力,即实现全局搜索。
针对算法搜索参数A的特性,结合已有的改进算法及本文算法进行对比分析。本文针对式(3)中r1的值,选择不同的值,分析其在4种a迭代算法中对GWO的搜索参数A进行仿真。
由文献[5]可知,灰狼算法中的参数r1、r2的取值为[0,1]之间的随机数。式(3)中,对搜索参数A的直接影响因子有r1和a。由于r1在算法的计算中是随机产生的,为了避免偶然性,因此本文对基准函数测试时,采用了多次测试求取均值的思想。
本文在分析对搜索参数A影响参数中,针对不同的r1取值进行仿真实验。当r1=0.5时,4种非线性参数控制策略对搜索参数A的影响曲线是重合的。故本文r1分别取0.15、0.25、0.55、0.75、0.85和0.95,根据式(3),运用MATLAB进行绘制仿真拟合曲线,其仿真结果如图2所示。
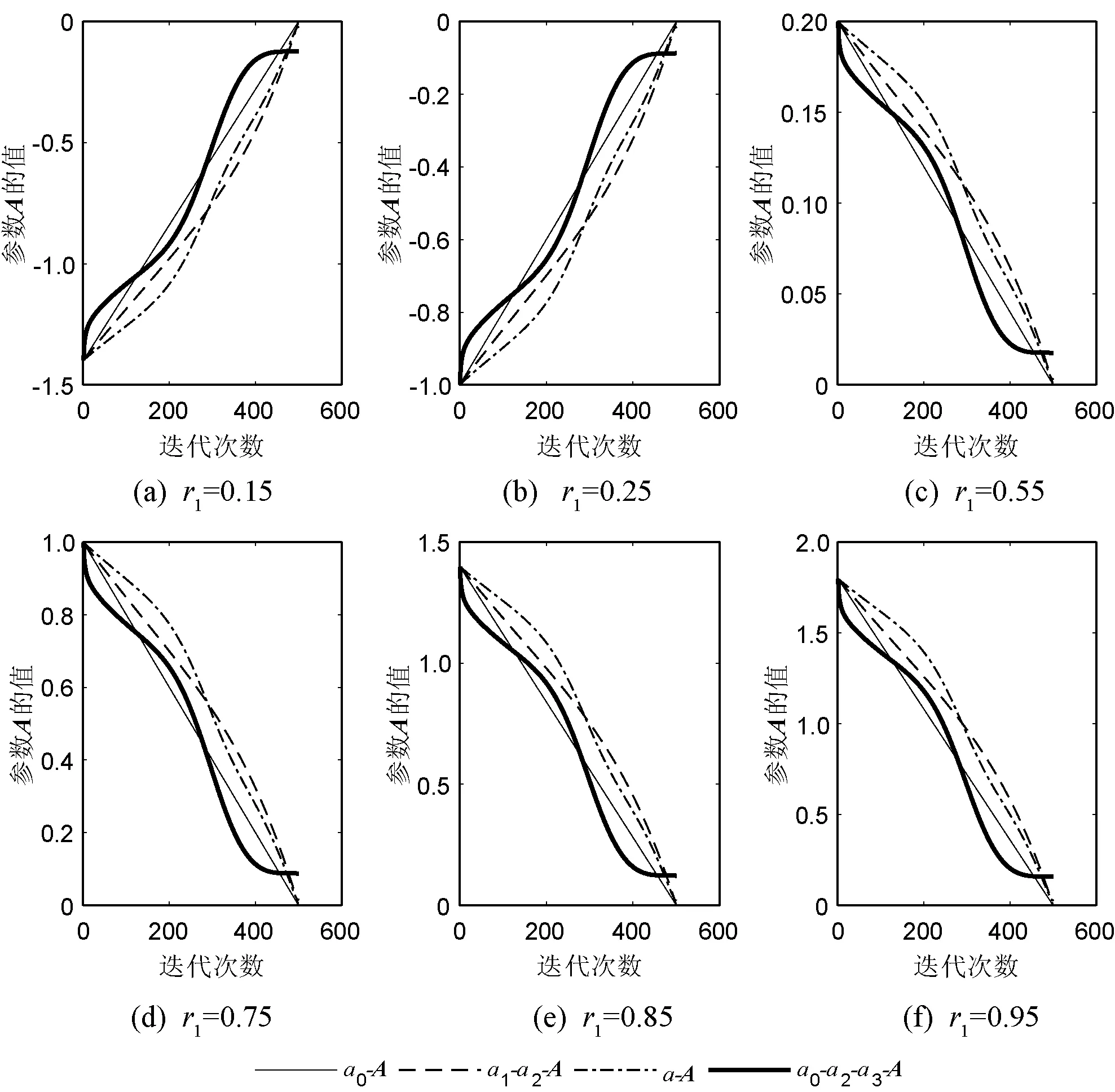
图2 4种a的迭代算法下的搜索参数A的拟合曲线
可以看出,本文提出的组合策略,以图2(d)为例,算法的迭代过程中搜索参数A曲线的斜率在不断地变化,前期的搜索参数A递减速度较慢可增强全局的搜索能力,可避免陷入局部最优;中期的搜索参数A递减速度较快从而改善算法的局部搜索能力,可加快算法的收敛速度;后期的搜索参数A递减速度有一个由慢到快的过程,可以在算法的迭代过程中进一步有效地均衡局部搜索和全局搜索能力。
2.5 改进的算法流程
本文策略对应的改进GWO步骤如下:
Step 1设置种群的规模N、维度d,初始化a、A和C的值;初始化Xα、Xβ和Xδ的值。
Step 2计算每个智能体的适应度值。
Step 3比较各智能体的适应度值及Xα、Xβ和Xδ的适应度值,确定当前的Xα、Xβ和Xδ的值。
Step 4根据本文策略,由式(10)、式(14)分别计算控制参数a的值,以及根据式(3)和式(4)分别对应计算A和C的值。
Step 5根据式(6)-式(8)更新种群个体的位置,再重新计算适应度值,并更新α、β和δ的值。
Step 6判断t是否达到Tmax的值,如果达到则结束,输出最优解,否则返回Step2继续执行。
3 实验与仿真分析
3.1 基本测试函数
为了验证基于权重系数改进的灰狼优化算法的有效性, 本文对表4中的6种基准测试函数进行仿真实验,并与基本的灰狼算法(GWO)[5]、本文提出的几种不同权重系数的改进灰狼算法的优化结果进行对比分析,并选择出相对较优的权重组合策略进行分析。表4中F1-F3为单峰函数,F4-F6为多峰函数。

表4 基准测试函数
3.2 实验参数的设置
本文的仿真实验中,算法的种群规模N为30,最大迭代次数Tmax为500, 控制参数初值afirst=2,终值afinal=0。非线性参数控制策略组合方式中的调节参数μ=2,λ=5,非线性调系数γ=10,算法开发和搜索能力影响因子k=6。本文采用MATLAB2014a进行仿真。
3.3 仿真分析
为验证权值系数的非线性参数控制组合策略及本文算法的性能优劣。针对同一测试的基准函数,对不同的参数控制策略对应的算法分别独立运行20次,并比较5种算法对6个基准测试函数的统计平均值(Mean)和方差(Std)。表5列出各算法在基准测试函数上的平均值(Mean)和方差(Std)结果。
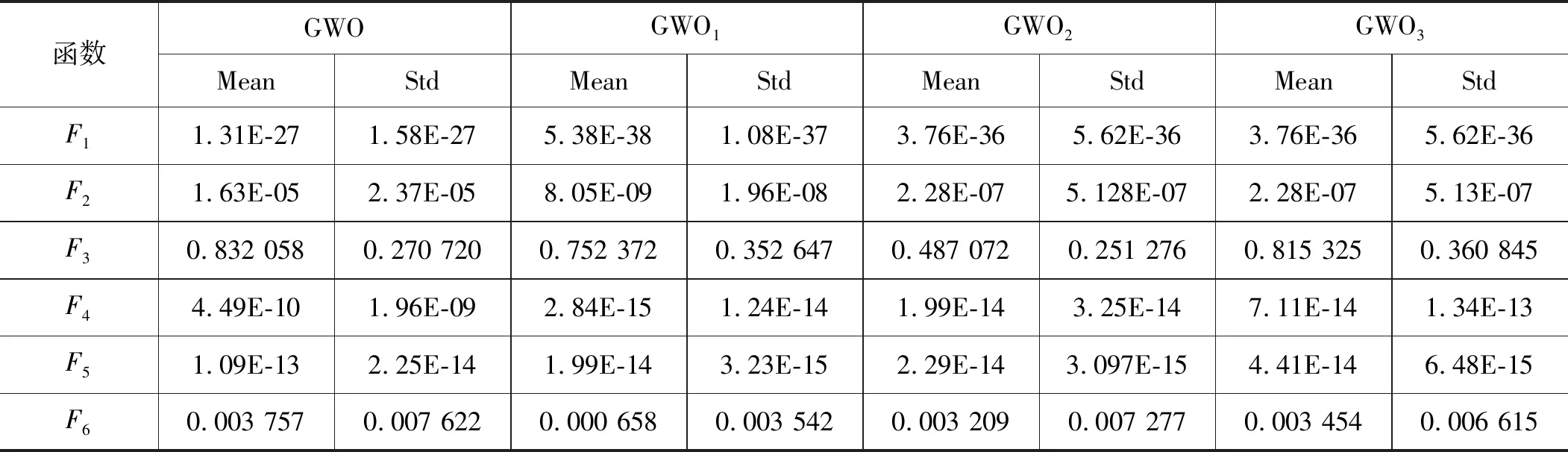
表5 GWO、GWO1、GWO2、GWO3的寻优结果
从数据可以得知,本文算法在μ=2、λ=5、γ=10、k=6时,对F1、F2、F4、F5、F6基准测试函数求解的平均值中,均优于传统的GWO、GWO2和GWO3。
为了进一步地说明本文策略的收敛性能,图3给出了4种参数控制策略的仿真结果对比。
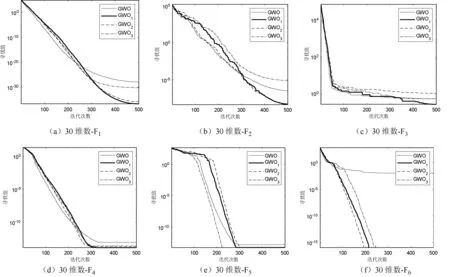
图3 4种不同调整参数控制策略的收敛曲线
可以看出,在搜索初期5种算法的搜索速度相近。随着迭代次数的增加,对于多峰函数,结合表5的结果可以看出非线性控制参数组合策略的GWO1寻优效果较好;对于单峰函数F3,本文算法要略劣于GWO2。这说明对于不同的函数,参数的取值会对算法的寻优结果产生一定的影响。因此,在智能算法的应用中,需要针对应用场景进行参数的选取,从而达到最佳的效果。
此外,对比文献[10]中的改进灰狼优化算法的函数测试结果,从与本文采用相同的测试函数F1、F4和F5来看,对于相同的维数(30)本文提出的2种非线性参数控制策略在测试函数F1和F5上的寻优解均优于文献[10]提出的改进灰狼优化算法。文献[10]对测试函数F1和F5解的均值分别为1.334 85e-27、2.772 9e-13,方差分别为7.313 0e-28、1.028 3e-13,而本文的组合策略的参数控制的灰狼优化算法(GWO1)、基于正弦函数的调整参数控制策略的灰狼优化算法(GWO-SIN)对基准测试函数F1和F5的寻优解详见表3。可以看出,本文提出的GWO1对于测试函数F4的求解亦可得到与文献[10]相同的结果。
4 结 语
本文提出一种非线性控制参数组合调整策略。首先,通过对3种非线性参数控制策略的调节因子的不同的取值进行仿真;然后,对5组不同的调节参数值进行基准函数的测试仿真,选择权重系数的非线性控制参数组合策略的最佳参数值。此外,为了验证本文策略的有效性及其优劣性,对6个基准测试函数进行仿真实验。仿真结果表明,本文策略均优于GWO2、GWO3、文献[10]提出的改进灰狼优化算法。未来将对改进的GWO的理论进行研究[12],并应用于工程约束优化问题。

