基于最大互信息系数和小波分解的多模型集成短期负荷预测
张振中 郭傅傲 刘大明 唐 飞
1(天水电气传动研究所集团有限公司 甘肃 天水 741020) 2(大型电气传动系统与装备技术国家重点实验室 甘肃 天水 741020) 3(上海电力大学计算机科学与技术学院 上海 200093)
0 引 言
负荷预测是智能电网发展过程中的一项重要任务[1]。准确的负荷预测对于电力系统调度和安全、可靠、经济的系统运行至关重要。现如今随着可再生能源并入电网、电动汽车的日益普及和配电网负荷需求的时变性,不可避免地增加了电力系统的复杂性、不确定性和非平稳性。
在短期负荷预测中,原始数据集选择和预测模型构建是近些年研究的两个重点领域。原始数据集特征提取方面,文献[2-3]采用Person相关系数分析对电力负荷进行特征选择。但由于电力系统相关数据是多维非线性的,采用线性相关的Pearson系数分析并不合适。历史负荷序列具有非平稳的特点,文献[4]利用小波分解将历史负荷分解为一系列平稳子序列进行预测,最后由重构得到最终预测。结果表明,非平稳的负荷经小波分解后将会得到更准确的预测结果。
在预测模型构建方面,机器学习模型由于对非线性序列具有良好的预测能力,从而被广泛应用于电力系统负荷预测中,代表模型主要有支持向量回归(SVR)、多层感知机(MLP)、深度学习和集成预测。由于单一模型在预测方面的泛化能力和预测精度不足,文献[5-6]采用多模型融合进行预测,提高了预测精度。
为提高负荷预测精度,本文提出一种基于最大互信息系数(MIC)与小波分解的多模型集成短期负荷预测新方法。首先采用MIC对多源特征进行选择,生成最佳特征集;然后经小波变换将提取出的非平稳负荷序列进行频域分解,生成平稳高通和低通分量信号;运用多模型预测算法对各分量信号进行训练,由重构得出各个模型的子预测结果;最后通过二次学习生成的决策模型集成并生成最终预测结果。对IESO官网公开的加拿大渥太华市真实电网数据进行实验分析,并与其他预测模型做对比,实验结果表明本文集成预测方法具有更高预测精度。
1 最大互信息系数
最大互信息系数(MIC)是2011年由Reshef等[8]提出的,它是在互信息(MI)的基础上发展而来的。互信息可看作一个随机变量由于已知另一个随机变量而减少的不确定度,主要用来衡量线性或非线性变量之间的关联程度。设x、y为随机变量,则互信息定义为:
(1)
式中:I(x;y)为变量x、y的互信息;p(x,y)为联合概率密度函数;p(x)和p(y)为边缘密度函数。两个变量之间互信息越大,则相关性越强。相较于互信息而言,MIC在MI基础上克服了互信息对连续变量计算不便的缺点,具有更高的准确度。当拥有足够的统计样本时MIC可以捕获广泛的关系,更能体现属性特征之间的关联程度[8]。
MIC计算主要分为以下三步:

2) 对所求最大互信息值除以log(min(m,n))归一化处理,将其转化到(0,1)区间;
3) 构建多种不同网格尺度m×n,依次代入式(1)和式(2)求得最大归一化互信息值作为最终MIC值。MIC的整体求值公式为:
(2)
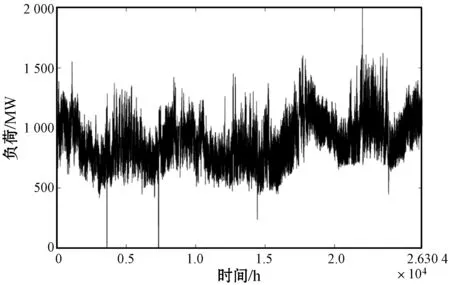
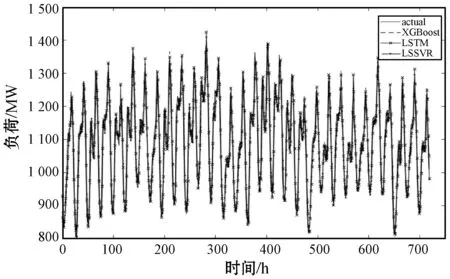
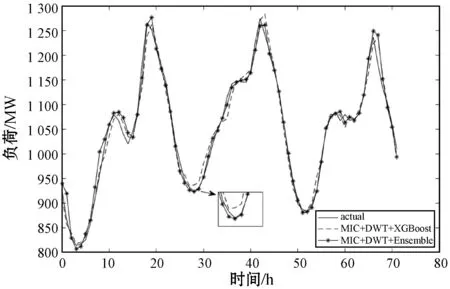
式中:m×n D=[Wi,M1i,M2i,…,D1i,D2i,…,li] (3) 式中:W为负荷所属日类型,定义W=1为工作日,W=0为周末或假日;M1i、M2i、…表示经MIC特征选择后的气象特征变量;D1i、D2i、…表示经特征选择后的日期类型特征变量;li表示历史负荷变量;下标i为对应负荷时刻的气象和日期类型变量,i=1,2,…,n,n为负荷值个数。 小波变换(Wavelet Transform,WT)是一种新的变换分析方法,它继承和发展了短时傅里叶变换局部化的思想,同时又克服了窗口大小不随频率变化等缺点,在信号处理、去噪等方面表现出强大的优越性[9]。本文利用小波变换将非平稳负荷相关数据分解成一组具有不同频率的本构分量。每个本构分量都由一个预测模型来预测。与原始发电序列相比,本构分量的方差稳定、平稳性好[4],因此可以更准确地进行预测。 小波变换可分为连续小波变换(CWT)和离散小波变换(DWT)两类。CWT可定义为: (4) (5) 式中:x(t)表示原始输入;ψa,b(t)表示母波信号,a、b分别为尺度因子和平移参数;*表示共轭复参数。DWT可通过对母波信号的离散化平移和缩放得到: (6) 式中:a=2m,b=n2m;T为离散点个数。负荷序列通过离散小波变换进行分解。将预处理后的负荷序列信号进行两级小波分解,分为一低频两高频信号。负荷序列两级分解的一个实例如下: l(t)=A1(t)+D1(t)=A2(t)+D2(t)+D1(t) (7) 负荷序列首先分为低频A1和高频D1信号。然后,低频A1被进一步分解成两个分量:A2和D2。低频近似分量A2反映了总体趋势,呈现负荷光滑形式。D1和D2描述了负荷中的高频分量。 利用母小波coif4对文中负荷时间序列分解,生成低频近似分量和高频细节分量,共3个子数据集。 在预测模型构建方面,为克服了单模型拟合过度和泛化能力有限的问题,在经特征选择和小波分解的数据集基础上,采用不同的机器学习算法构建出异构集成预测模型,利用多算法的互补优势来解决单一算法精度低和应用有限的问题[10]。 在负荷预测中,LSSVR是支持向量回归的一种扩展,其将SVR算法的不等式约束转换为等式约束,大大方便了Lagrange乘子α的求解,降低了计算复杂度,且由于待选参数少、求解速度快的优势,被广泛地应用于电力系统负荷预测中。LSTM是普通循环神经网络RNN衍变出的一种变种模型,能够建立先前信息与当前环境之间的时间相关性,克服了普通RNN在训练反传过程中出现的梯度消失等问题,因其中含有记忆单元,非常适用于处理和预测长时间序列问题。XGBoost是一种对异常值具有较强鲁棒性的树型算法,并在工程实现上做了大量优化,是目前具有良好分类和预测的机器学习方法之一,且用于模型训练的设置参数较少,该方法能有效克服过拟合问题,预测性能优于渐近梯度回归树和随机森林。 因此,本文首选LSSVR、LSTM和XGBoost三种异构预测模型来分别训练经MIC特征选择和小波分解后的数据集,最后通过小波重构得到对应的预测结果。其中:原始数据的前90%作为训练集,后10%作为测试集。训练集中每前一个星期数据(包括负荷、天气、日期类型数据)作为训练输入,训练输出为当天的负荷数据。 多模型融合预测的集成方法主要有四类:简单平均法、加权平均法、线性模型训练集成和非线性学习模型训练集成等。简单平均法和加权平均法只是将多模型的预测输出作为变量,然后采取简单措施得出一个最终结果,但是忽略了原始数据集特征,所得最终输出效果不佳。而二次学习则是在原始特征和上一阶段预测输出的基础上训练一个新的学习模型,通过参数调整得到集成决策模型。然后将多模型的预测结果作为决策模型的输入并由决策模型训练学习得到最终预测结果。 学习模型主要包括线性模型和非线性学习模型。由于时序电力负荷呈非线性,线性模型在处理非线性数据时预测精度较低,鲁棒性差。而非线性模型却可以很好地对电力负荷数据进行处理。 二次学习决策模型训练方法: 1) 原始训练集(包括原始负荷及相关影响因素特征)和各个预测模型的输出结果组成新的训练集。利用经训练后的多模型对预测前K小时负荷进行预测,将预测负荷(LSS1,LSS2,…,LSSk),(LST1,LST2,…,LSTk),(XGB1,XGB2,…,XGBk)作为新特征加入到原始训练集中,得到新的训练特征集: DS=[Wi,M1i,M2i,…,D1i,D2i,…,li, LSS1,LSS2,…,LSSk,LST1,LST2,…,LSTk XGB1,XGB2,…,XGBk] 2) 将步骤1)所得的新训练集分别输入至非线性预测模型(LSSVR、LSTM、XGBoost)进行再次训练学习,通过以损失函数最小为目标进行参数调整,最后找出训练良好、预测精度高的模型作为决策模型。如图1所示。 图1 二次学习生成决策模型的训练过程 设计的预测方法总体流程如图2所示,可分为四个阶段。 图2 预测方法总体流程 1) MIC特征选择及处理:对原始数据集利用MIC特征选择技术选出与历史负荷相关性较大的因素,并生成输入特征序列。 2) 小波变换:在上一步基础上,利用小波变换将非平稳负荷序列进行两级小波分解,转换为较为平稳的负荷相关序列,更有利于负荷预测。 3) 异构多模型集成预测:利用较强泛化能力和预测精度的LSSVR、LSTM、XGBoost三种机器学习模型对小波分解后的平稳信号训练学习,由模型重构得到每种模型的预测输出。 4) 二次学习:将三种不同预测模型输出的结果同原始特征集组成新的训练集,输入到预测性能优越的模型进行再次训练学习,经调参后得到训练良好的决策模型。最后由决策模型得到最终预测结果。 实验选用加拿大渥太华市2016年到2018年三年真实电网数据(一天24数据点)、气象因素(温度、风速、湿度)、日期类型(年、月、日)为例。原始负荷数据集如图3所示。 图3 原始负荷数据集 由图3可知,负荷数据集中存在个别异常值,为简单处理,可直接将其剔除。然后由最大互信息系数对日负荷相关影响因素进行特征选择,如表1所示。 表1 MIC特征选择 样本数据量越大,达到显著性相关的系数就会越小。本文最终选取了温度特征变量同相应的历史负荷一同作为预测模型的输入,输入特征集D为: D=[Wi,temp1,temp2,…,tempi,l1,l2,…,li] 式中:W为待预测负荷所属日类型;tempi表示温度特征变量,li表示历史负荷变量;i=1,2,…,n,n为输入负荷值个数。 数据集经预处理后,利用两级小波分解将历史负荷变量变换为平稳序列,分解后序列如图4所示。 (a) A2 (b) D2 (c) D1图4 负荷序列小波分解 此预测方法运行在个人PC(配置为CoreI7处理器、8 GB RAM和DDR3存储)的Python 3.6环境下。经训练学习后三类模型主要参数选择如表2所示。 表2 各模型参数选择 将平均绝对百分比误差(MAPE)、均方根误差(RMSE)和平均绝对误差(MAE)作为误差评估指标,其公式分别如下: (8) (9) (10) 经上述MIC特征选取和DWT小波分解后的负荷子序列及对应特征作为预测模型输入。其中,三个子序列分别由同种预测模型进行训练学习,最后由小波重构得出预测结果。本文采用了近几年在负荷预测领域表现良好的多种机器学习模型(LSSVR、LSTM、XGBoost)进行预测。一个月的预测结果如图5所示。 图5 单一预测模型对比 月负荷预测评估结果如表3所示。可以看出,XGBoost、LSTM和LSSVR的MAPE分别为1.28%、1.33%、1.47%,上述单一模型均具有较好负荷预测能力。 表3 月负荷预测评估结果 为进一步提升预测模型的整体预测精度和泛化能力,采用了XGBoost、LSTM和LSSVR进行多模型融合预测,融合阶段由二次学习得到的非线性决策模型进行集成融合,决策模型的选择则是根据上述实验得出。XGBoost相较于LSTM、LSSVR具有更高的预测精度,且XGBoost是由多个同构决策树集成所得,泛化能力强,所以本文选择XGBoost作为决策模型。 为了验证所提的基于最大互信息系数和小波分解的XGBoost负荷预测模型的有效性,本文将所提模型预测结果与上述单一模型中表现最好的XGBoost进行比较,预测未来三天的负荷值(2018年12月29日—2018年12月31日),所得结果如图6所示。 图6 单一与集成预测模型对比 经进一步分析对比可得出,本文方法集成方法(MIC+DWT+Ensemble)的预测值和真实值的偏差明显小于预测效果最好的单一模型MIC+DWT+XGBoost的预测结果,它们的MAPE分别为0.91%、1.24%,如表4所示。 表4 负荷预测评估结果 实验结果表明,经多模型融合的集成预测模型预测效果高于预测性能良好的单一预测模型。通过MIC特征选择与DWT小波分解为平稳负荷序列后,由预测性能较好的模型对每个近似和细节平稳分量进行预测,然后由重构得出三种不同预测结果,这些预测结果在同一小时内是不同的,最后通过非线性二次学习将上述预测结果融合作为最终输出,可进一步提高负荷预测精度。 时序电力负荷具有非平稳特性且受多种外在因素影响。单一预测模型在复杂电力系统中存在预测性能和泛化能力低的缺陷,较难满足电力调度的要求。本文提出了一种基于最大互信息系数与小波分解的多模型集成短期负荷预测模型,并通过真实电网数据进行了验证。得出以下结论:1) 影响负荷的因素众多,利用适用于非线性数据的最大互信息系数选出与负荷相关性较大的影响因素,并将所选因素与历史负荷一同作为预测模型输入,可提高预测精度。2) 在预测模型方面,通过小波分解将非平稳的负荷序列转换成一组相对平稳的本构分量,更适用于负荷预测。3) 由预测性能良好的单一模型融合后生成的集成模型,可有效避免过拟合和梯度消失问题,进一步提升负荷预测精度和泛化能力,在实际应用中更具有价值。2 小波变换
3 多模型集成
3.1 多模型构建
3.2 二次学习

3.3 总体流程
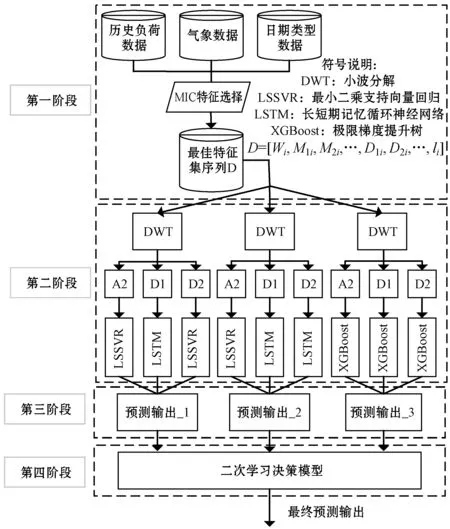
4 算例结果与分析
4.1 特征集选取与小波分解

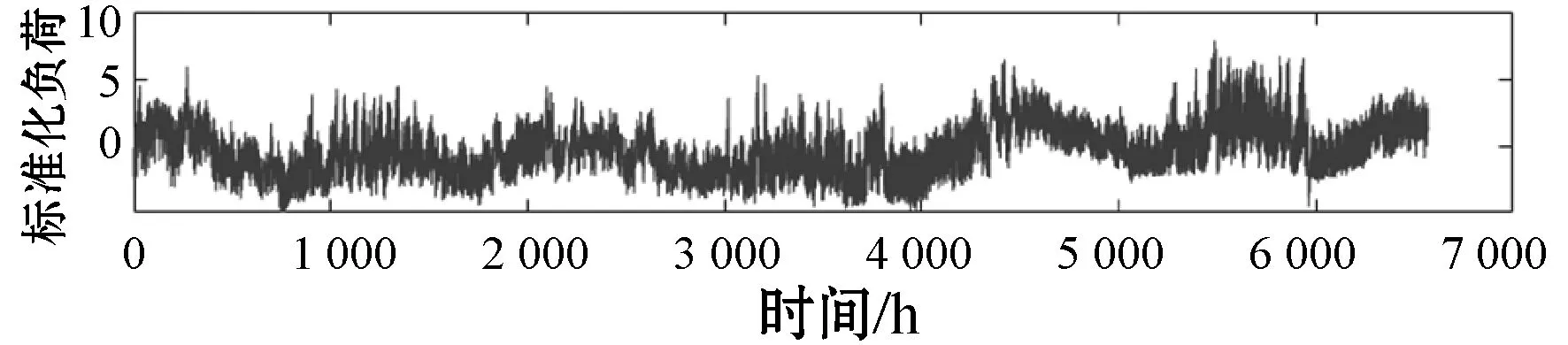

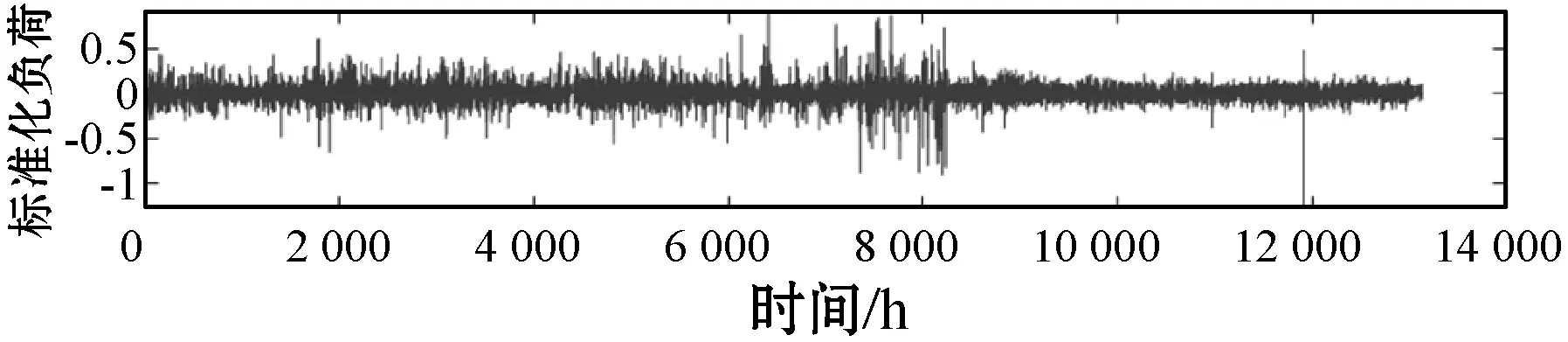
4.2 模型参数选择

4.3 评估指标
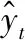
4.4 结果与分析

5 结 语

