基于DCAE-SVM的变压器故障诊断
郝玲玲 朱永利
(华北电力大学控制与计算机工程学院 河北 保定 071003)
0 引 言
变压器是电力系统的核心设备,保障其安全运行至关重要,因此,提前对变压器进行故障诊断尤为关键[1]。可以根据油中溶解气体的浓度与变压器故障之间的关系来预测故障,常用的方法就是油中溶解气体分析法(Dissolved Gases Analysis,DGA)[2]。基于DGA的故障诊断方法通常有人工神经网络(ANN)[3]、极限学习机(ELM)[4]和贝叶斯分类器[5]等算法,其中:人工神经网络的训练速度慢;极限学习机的运行速度快,但稳定性差;贝叶斯分类器则需要将大量样本数据进行实验才能得到较好的效果。因此,如何在现有方法的基础上提高诊断准确率成为了重要问题。
随着智能化的普及,越来越多的机器算法被用在变压器诊断中。文献[6]在变压器诊断中采用深度自编码器的方法,诊断精度高于传统算法;文献[7]将降噪自编码器应用于油色谱异常数据的特征提取中,但是特征提取的效果并不理想;文献[8]将堆栈降噪自编码器用于变压器诊断中,诊断性能较好;文献[9]将堆栈降噪自编码器与支持向量机相结合应用于压力机轴承故障诊断中,故障识别度较高;文献[10]将多分类最小二乘支持向量机用于变压器诊断中,与传统方法比诊断率较高。虽然上述文献将几种不同的自动编码器应用于变压器故障诊断中,但特征提取能力及诊断准确率还有一定的不足之处。
本文针对目前存在的变压器故障样本少及无标签样本无法充分利用的情况,提出了基于深度收缩自编码器(DCAE)与支持向量机(SVM)相结合的混合诊断模型。该混合模型通过大量无标签样本数据训练DCAE网络,自动更新网络参数,然后用有标签样本对DCAE-SVM网络的参数进行微调和进一步优化,实现故障预测。实验结果表明变压器诊断准确率明显提高了。
1 DGA故障诊断原理
DGA是通过获取变压器中的油色谱监测数据来预测可能出现的故障类型,监测的主要是几种气体(氢气H2、甲烷CH4、乙烷C2H6、乙烯C2H4和乙炔C2H2)的浓度变化值,而且最终的故障类型主要包含热故障和电故障两种,具体分为中低温过热、高温过热、局部放电、高能放电、低能放电和正常情况6种状态。
2 DCAE-SVM模型
2.1 深度收缩自编码模型
深度自编码器[11]是由多个自编码器(AutoEncoder,AE)叠加而成,逐层依次训练每个自编码器,有效提高了单层网络训练效果不理想的情况。Vincent等[12]为了提高自编码器的鲁棒性,在自编码器的基础上提出了降噪自编码器(Denoising AutoEncoder,DAE)。本文所采用的收缩自编码器(Contractive AutoEncoder,CAE)[13-16]就是在AE的基础上为了进一步提高自编码器的鲁棒性而提出的。
DAE网络是在原始输入数据上添加噪声,然后再尽可能地重构出原始数据,从而达到提高网络鲁棒性的目的。CAE网络是在传统AE网络重构误差的基础上添加了一个新的雅克比矩阵项,以此来保证自编码器在较小数据扰动的情况下有更强的鲁棒性。DAE网络是在重构函数处的鲁棒性较高,能抵抗小的数据扰动情况;而CAE网络依靠提取更准确的样本特征,在特征提取处的鲁棒性高,能抵抗微小的输入扰动,其结构图如图1所示。
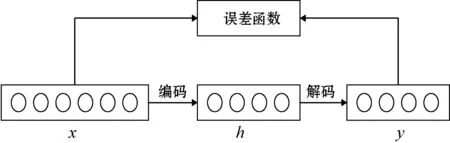
图1 收缩自编码器结构
原始输入数据用向量x={x1,x2,…,xn}表示,通过自编码器将输入数据映射到隐含层,表示为h={h1,h2,…,hm},然后通过解码器在特征空间重构输入数据并输出为y={y1,y2,…,yn},最后通过最小化重构误差优化网络参数,最大程度地重构原始数据。本文采用的编码器、解码器和重构误差函数如下。
(1) 编码 编码器将原始输入数据通过函数映射实现从输入层到隐含层的编码过程,具体原理可表示为:
h=fθ(x)=Sf(Wx+b)
(1)
式中:θ={W,b}为模型参数;W为权重矩阵;b为输入层的偏置向量;Sf为激活函数,本文用的是sigmoid函数,表示为:
s(t)=1/(1+exp(-t))
(2)
(2) 解码 解码器将隐含层编码h映射到输出层y,并使得输出层y的值与输入层x的值尽可能相近,具体解码原理可表示为:
y=gθ′(h)=s(W′h+b′)
(3)
式中:θ′={W′,b′}为解码器的模型参数;W′为解码器的权重,且W′=WT;b′为隐含层的偏置向量。
(3) 重构误差函数 编码器尽可能地缩小重构误差以此来达到优化网络参数的目的,CAE的重构误差函数是在原函数的基础上加了雅克比矩阵构成的,原本的自编码器重构误差表达式为:
(4)
式中:L为重构误差,本文选用的是均方根误差(Root Mean Squared Error,RMSE),表达式为:
(5)
式中:m为样本数,xi为输入向量,yi为输出向量。所以,CAE的重构误差函数可表示为:
(6)
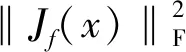
(7)
因此,雅克比矩阵中F范数的平方和也可以表示为:
(8)
式中:hi为隐含层的输出值,Wij为输入层到隐含层的连接权重。
本文通过叠加多层CAE构成深度收缩自编码器(Deep Contractive AutoEncoder,DCAE),也就是将上一层CAE隐含层的输出作为下一层的输入,其网络结构图如图2所示。
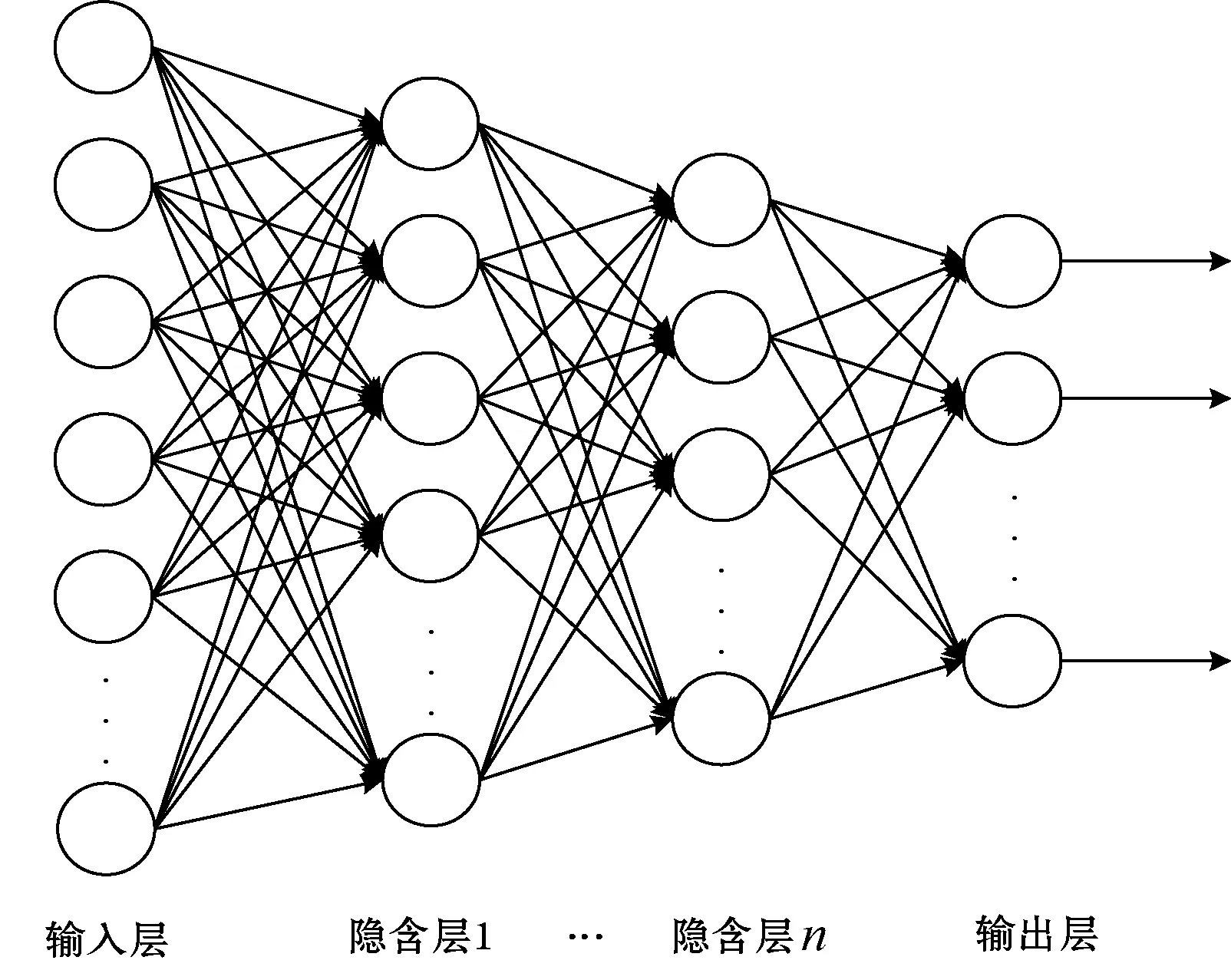
图2 DCAE网络结构图
2.2 支持向量机模型
支持向量机(SVM)[17]是现在较为常用的分类方法,在二分类、小样本模式识别等方面均已取得了一定的成果。
为了实现对样本的分类,SVM可以选择不同的核函数,将样本数据从低维映射到高维空间,从而找到一个超平面将其分为不同的类型,假设训练样本集为:{(ui,vi),i=1,2,…,n},其中ui为类属性,vi为类标记,n为样本个数,则超平面可定义为:
(9)
式中:ai为拉格朗日因子,K(u,ui)为核函数,b为偏置量。本文核函数选用的是高斯径向核函数:
(10)
传统的SVM针对的是二分类问题,因此,本文将变压器诊断分解为多个二分类问题相结合的方法。针对变压器故障诊断来说,需要使用5个二分类器,第一次分类区分的是故障和正常两种情况,第二次区分的是热故障和放电故障,之后三次分类就详细区分具体的故障,模型图如图3所示。
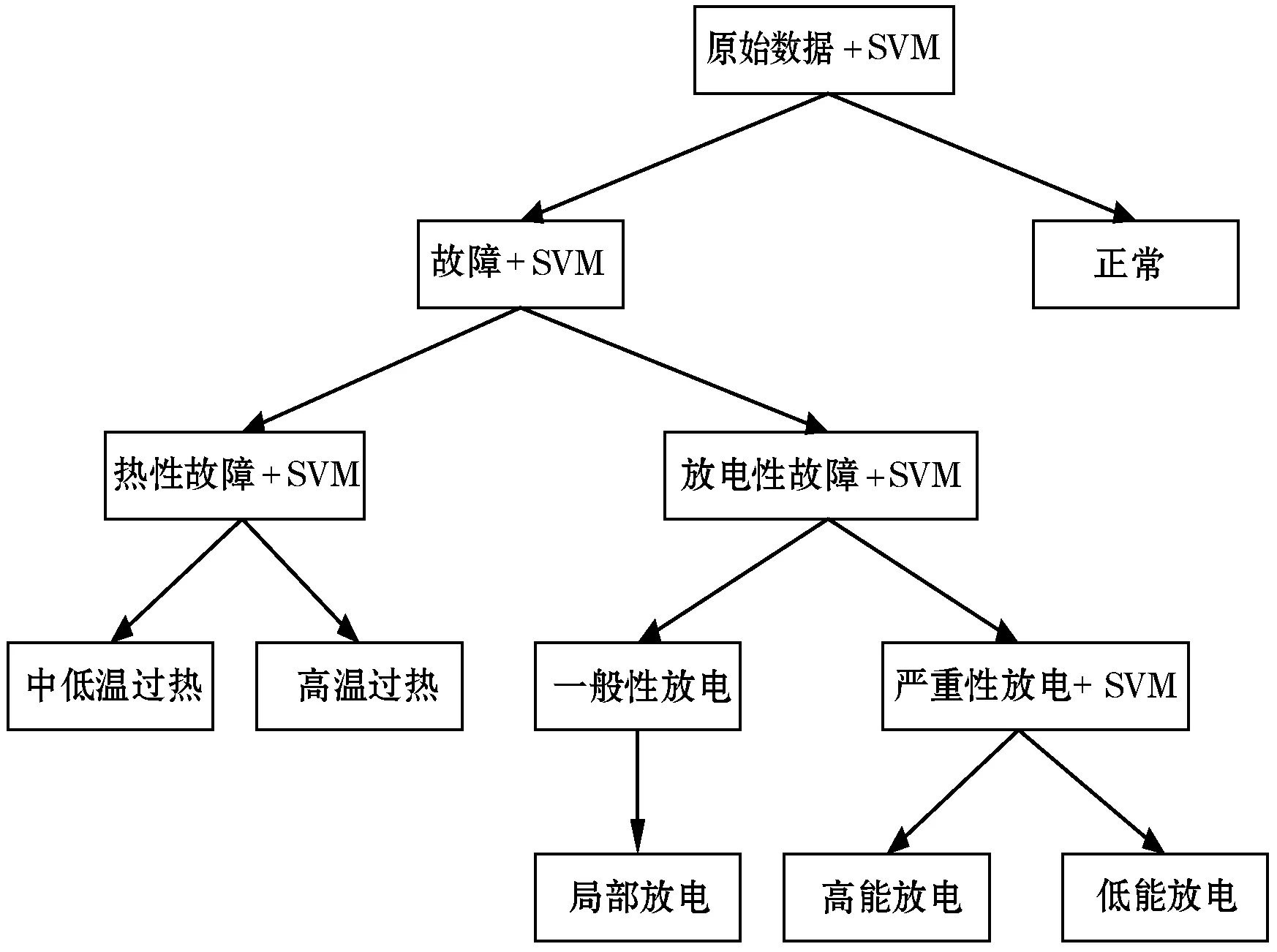
图3 SVM多分类故障诊断模型
2.3 DCAE-SVM的混合模型
本文首先用无标签样本数据训练DCAE网络,初始化并调整网络参数,然后采用有标签数据对DCAE-SVM模型参数进行调优,最终得到优化后的DCAE-SVM故障诊断模型,具体步骤如下:
(1) 对数据集进行标准化处理,并划分成训练集与测试集两部分。
(2) 设置DCAE网络参数,并初始化模型。
(3) 使用无标签样本训练DCAE网络,并自动调整每一层的参数W和b,将调整好网络参数的DCAE模型作为预训练模型。
(4) 用一部分有标签样本调整DCAE-SVM混合模型参数,得到优化后的网络模型。
(5) 用剩下的有标签样本进行故障诊断测试,并计算诊断准确率。
3 基于DCAE-SVM的变压器故障诊断
3.1 数据的选取和预处理
本文选用的故障样本是从同一型号的变压器上采集的,共包含1 500组无标签样本和360组有标签样本,将其中1 500组无标签样本作为训练集,360组有标签样本中的180组作为调优集,另外180组作为测试集。
根据DGA数据的特点,首先对五种典型气体的含量值进行标准化处理,然后将其作为DCAE网络的输入值。标准化公式如下:
(11)
式中:xnew是标准化处理后的气体值;x为气体原始值;xmean表示数据集中该类气体的平均值;xmax表示该类气体中最高值;xmin表示该类气体中最低值。
3.2 变压器状态编码
变压器故障诊断结果共有6种类型,编码情况如如表1所示。
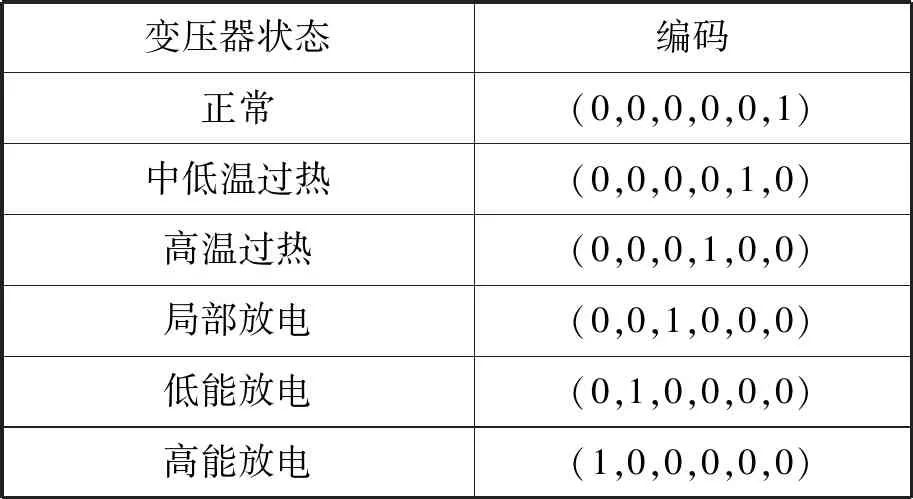
表1 变压器状态编码
3.3 参数测试与分析
本文采用MATLAB R2016a平台测试算法性能,硬件环境为Lenovo,i5- 7300处理器,64位操作系统,8 GB运行内存。
DCAE网络预训练阶段需要首先确定隐含层层数和隐含层节点数,然后设置迭代次数为1 000,学习率为0.01,网络的权值矩阵W和偏置系数b都是随机生成的较小数值。
(1)隐含层节点数 设收缩自编码器隐含层层数为1层,输入1 500组无标签样本数据分别测试了隐含层节点数为0~100时的均方根误差(RMSE),实验结果如图4所示。
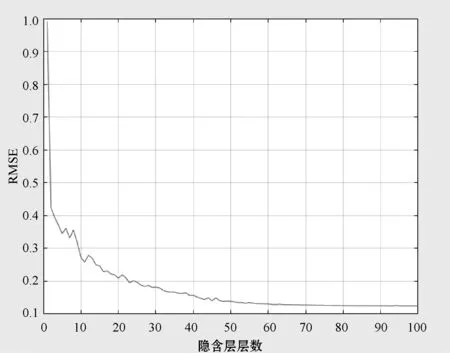
图4 隐含层节点数与RMSE的关系图
可以看出,当隐含层节点数小于50时,随着隐含层节点数的增加,RMSE的值有明显下降的趋势;当节点数在50~60之间时,RMSE的值下降趋势变得缓慢;而当节点数在60~100之间时,RMSE的值几乎不变。因此,最终选用的隐含层节点数为60,若隐含层层数增加,则隐含层节点依次选取前一层一半的节点数会使得实验结果较优。
(2)隐含层层数 设收缩自编码器的隐含层层数为1~7,隐含层节点数按层数依次为:60,30,15,8,4,2,1,并以1 500组无标签DGA数据作为输入进行实验,得到网络输出的均方根误差,如图5所示。
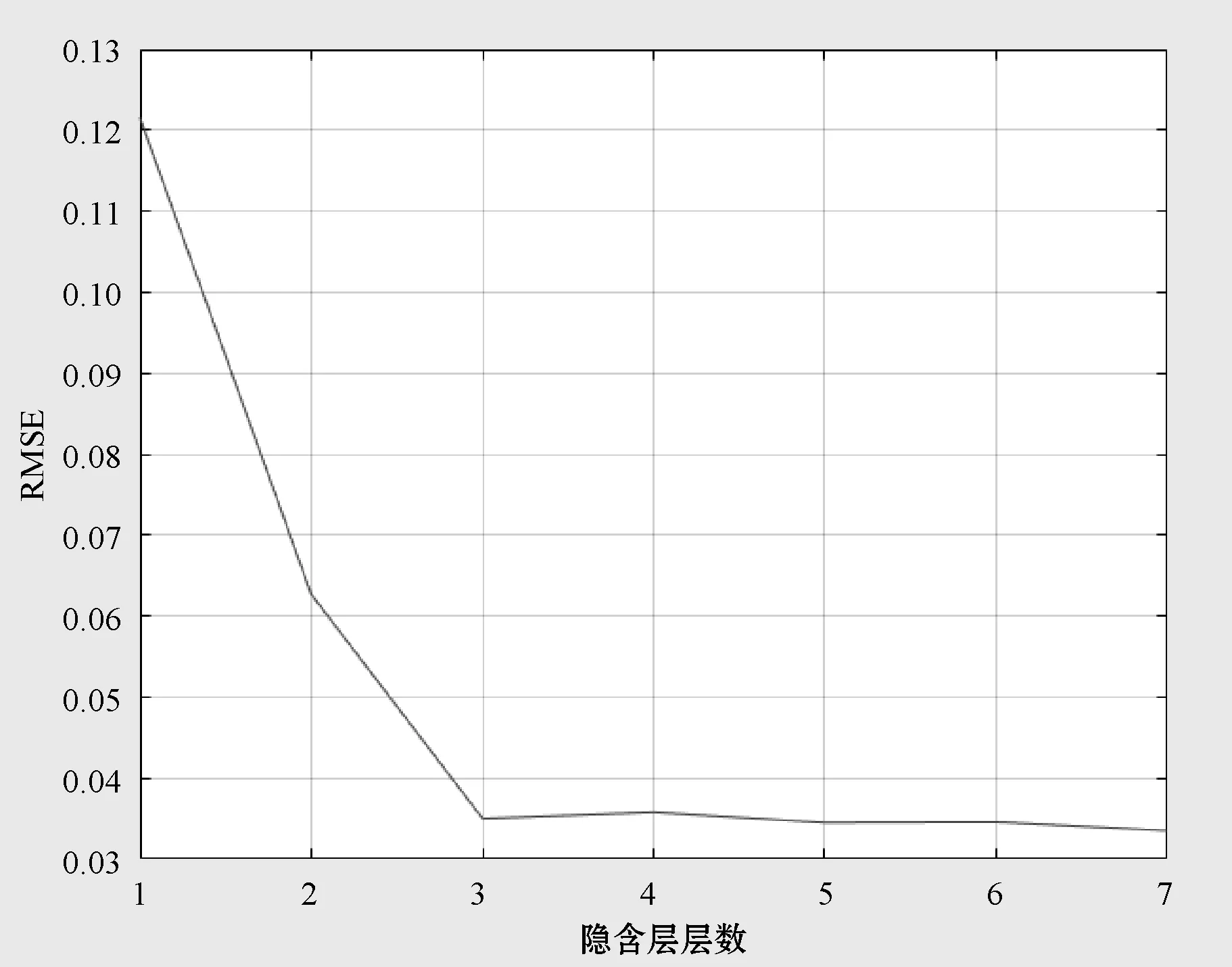
图5 隐含层层数与RMSE的关系
可以看出,当隐含层节点数在1~3之间时,RMSE的值下降得很明显;而当隐含层节点是在3~7之间时,RMSE的值逐渐趋于稳定。因此,本文选取的隐含层层数为3层,每层节点数分别为60、30、15。
3.4 结果测试与分析
本文首先对比了在隐含层层数与隐含层数量都相同情况下的深度收缩自编码器与堆栈降噪自编码器的RMSE的值,如图6所示,其中:选用1 500组无标签数据进行实验,堆栈降噪自编码器的隐含层层数为3层,隐含层节点数分别为60、30、15,学习率为0.01,噪声比例为0.2。

图6 两种自编码器的RMSE值对比
可以看出,隐含层节点数量在0~100之间时,几乎都是本文选用的DCAE网络的RMSE的值更低,表明使用DCAE网络输出的特征值比使用堆栈降噪自编码器输出的特征值与输入的特征值更加接近。
其次,用180组有标签数据集微调DCAE-SVM模型,其中模型的输入数据为180组标准化处理后的5种气体含量值,中间经过三个隐含层,将提取到的特征数据传送到SVM中,输出6种故障类型的编码值,并与原本给定的故障类型进行比对微调,得到最优的网络模型。最终,用另外180组有标签样本数据集进行测试,并计算出分类准确率。
为更明显地对比出实验效果,本实验分别选用有标签样本中的120组数据、150组数据和180组数据作为训练集。另外180组数据作为测试集,而且将提前训练好DCAE的DCAE-SVM模型与传统的BP神经网络、SVM模型进行对比,实验结果如表2所示。其中BP神经网络的迭代次数与学习率的值均与DCAE网络一致,SVM均选用RBF核函数,惩罚系数C设为80,参数Gamma设为0.008。
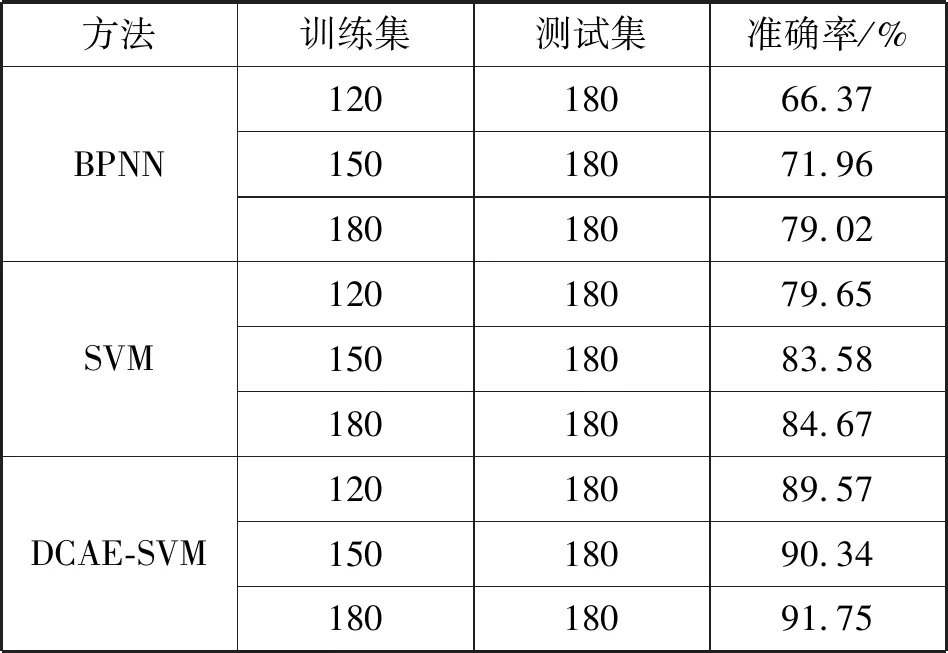
表2 不同训练集时基于SVM和DCAE-SVM的结果对比
从表2中可以看出,随着训练集数量的增加,诊断准确率均有所上升,但是本文采用的DCAE-SVM模型的准确率更高,而且准确率变化幅度更小,说明DCAE-SVM算法前期能够有效利用大量无标签样本数据,提取出更有效的样本特征,从而提高了预测准确率。
另外,在分类算法实现过程中,F1指标是非常常用的模型效果判别方法,需要根据各种变压器状态的准确率和召回率来计算出F1-Score、Micro-F1和Macro-F1三个指标值,精确率的计算式为:

(12)
召回率的计算式为:

(13)
F1-Score又称平衡F分数法,计算式为:
(14)
Micro-F1又称微平均法,是将变压器6种状态的精确率之和以及召回率之和代入式(14)中计算出的;Macro-F1又称宏平均法,是将每一种变压器状态的精确率与召回率都分别代入到式(14)中,然后将6个F1-Score的值取平均值得到的。
本实验选用180组训练集与180组测试集对DCAE-SVM方法的一次诊断结果做进一步的判定,详细预测结果如表3所示。
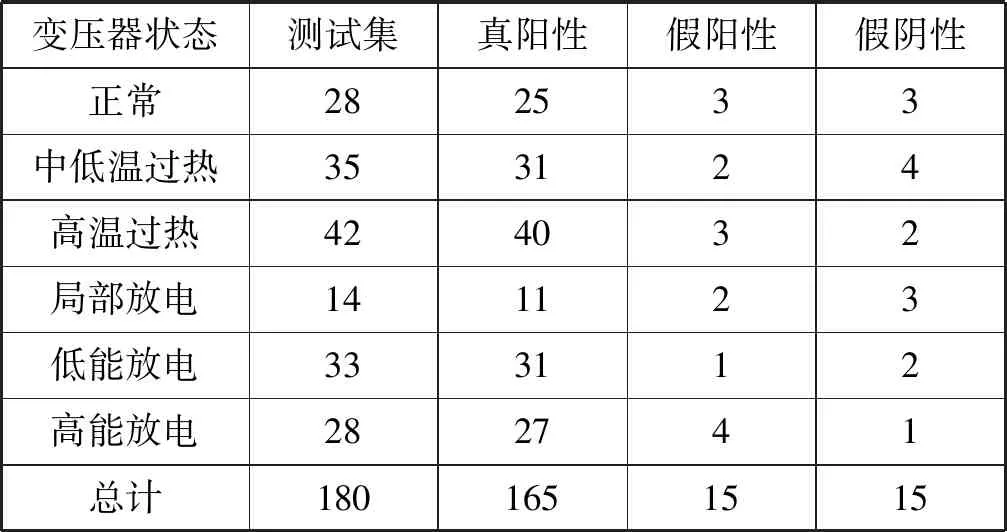
表3 详细预测结果
由表3的实验结果可以计算出DCAE-SVM方法的精确率、召回率,以及F1-Score值,如表4所示。
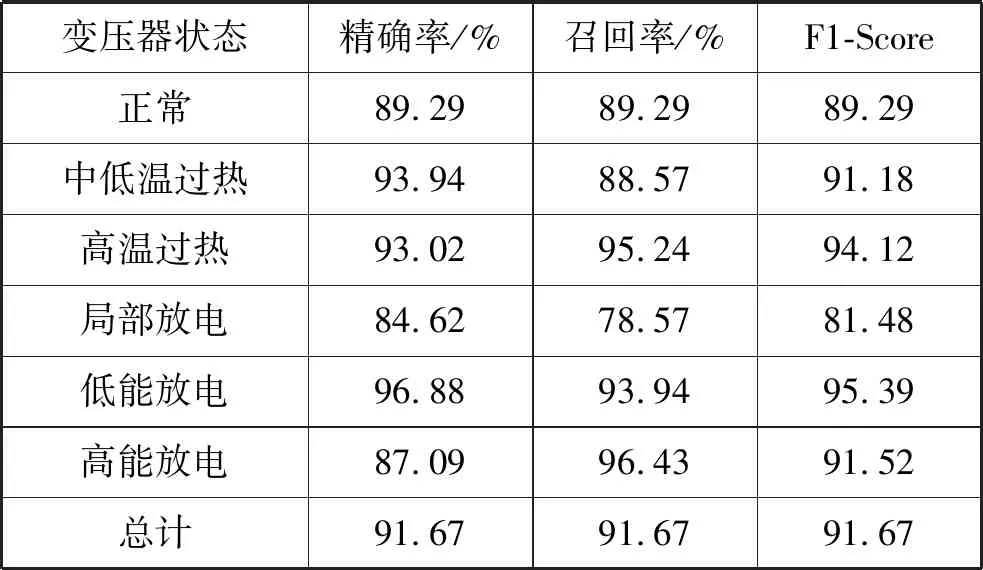
表4 精确率与召回率结果
因此,由式(14)与表3、表4可得到Micro-F1的值为0.916 7,Macro-F1的值为0.905 0,而采用BPNN以及SVM方法计算出的Micro-F1值与Macro-F1值均不超过0.85。这表明本文采用的DCAE-SVM的变压器故障诊断分类方法是有效的。
4 结 语
针对目前常用的变压器故障诊断方法存在诊断准确率不高、无法充分利用无标签样本等问题,本文采用了基于DCAE-SVM的变压器故障诊断方法,实验结果证明,深层的DCAE-SVM模型不仅可以更好地利用无标签样本数据进行训练,而且特征提取能力高于常用的堆栈降噪自编码器,故障诊断率高于常用的BP神经网络和SVM,是一种有效的变压器故障诊断方法。

