考虑动态临界加速度的地震边坡永久位移预测模型研究

刘爱娟, 崔玉龙, 刘铁新

(1. 中国长江三峡集团有限公司, 北京 100038; 2. 安徽理工大学土木建筑学院, 安徽 淮南 232001;3. 大连海事大学土木工程系, 辽宁 大连 116026)

0 引言

边坡在地震影响下破坏程度的判定依据以边坡稳定性分析为理论基础。目前地震边坡稳定性分析方法主要有拟静力法、数值分析法和永久位移法。其中永久位移法又称Newmark位移法,由Newmark[1]于1965年提出。Newmark位移原本作为一种判断指标应用在堤坝稳定性分析中,后来越来越广泛地应用于边坡稳定性分析。在区域边坡地震危险性评价中,为了计算出Newmark位移,需要有当地的加速度时程曲线。然而,特定地点的地震加速度记录并不容易获取,所以Ambraseys和Jibson等人在Newmark提出的临界加速度比的基础上发展了经验性的回归关系并在后期进行了改进,称为永久位移预测模型,以此作为对无强震记录地区地震边坡危险性评估的计算依据[2-5]。永久位移预测模型主要建立永久位移DN与地震动峰值加速度PGA、边坡临界加速度ac以及阿里亚斯强度IA之间的函数关系,是一种建立在统计学意义上的关系模型,可以在具有相应已知参数的情况下求取其他参数。此后,Roberto Romeo、徐光兴、Shang-Yu Hsieh、宋健、高广运、肖莉、Ren Mao-yuan等多个国家的研究者也根据所研究地区的实测地震资料做出了符合本地区区域特征的模型表达式[6-12]。目前,国内外已有大量文献[13-23]利用位移预测模型计算边坡地震时产生的永久位移并进行区域范围内的边坡地震危险性分析与评价。

然而,永久位移预测模型及其理论基础仍然存在着很多问题,主要表现为以下两个方面。

(1) Newmark永久位移法在计算边坡永久位移时假设抗剪强度在地震时程中是保持不变的,由此也假定临界加速度也是保持不变的。但实际上,在地震作用过程中,随着时程的延长,边坡潜在滑动面上的抗剪强度是逐渐减小的。在1965年原文中,Newmark意识到了这种保持常量的抗剪强度以及临界加速度是不合理的,他建议在使用该方法计算永久位移时考虑抗剪强度以及临界加速度的变化[1]。然而,这个建议并未被后续使用者重视并加以研究。

(2) 通过比较预测位移与滑坡实测位移的关系,研究者发现许多地震滑坡案例都存在预测位移小于实测位移的问题。例如Al-Homoud等[24]利用六种经验公式预测了地震作用下边坡的永久位移并与震后实际灾害调查结果进行对比,发现预测位移比实际位移偏小。Meehan[25]利用122处大坝和堤防的震后位移观测数据检验了15种位移预测模型的可靠性,结果均显示无论平均值还是上限值,所有预测地震位移都小于实际监测结果。在Meehan研究的大部分实例中,预测数据和观测数据之间的差别很大,一般都超过1 m。所以,Meehan提出设计者在使用这些位移预测模型时,一定要注意预测值和实际值之间的数值差异。

目前,针对预测位移小于实测位移的原因有以下解释:(1)在Newmark永久位移法假设条件中,滑块底面上的临界加速度是保持不变的,这就人为高估了斜坡在经受地震时的抵抗能力,从而造成预测位移小于实际位移。(2)预测永久位移是假想滑面上的位移值,而且只是在地震持续时间内的位移值。实际上,一旦滑面贯通,很难判断并区分后续的滑动是由地震造成还是由坡体本身重力造成。(3)Newmark永久位移理论以无限斜坡模型为假设状态,斜坡长度为无限长。实际滑坡在到达坡底后的运动状态已经不再是无限斜坡模型中的状态,其位移产生的途径已经脱离了Newmark法的初始假设条件,后期产生的位移并不适宜继续用Newmark法计算。(4)地震滑坡的实际观测位移一般包含同震位移和震后位移两部分。由于震后降雨等原因会使滑坡滑面的孔压增加,极易在大量余震作用下形成不容忽视的震后位移。目前还不能在观测位移中清晰区分同震位移和震后位移,Newmark永久位移仅计算同震位移,因此通常小于观测结果[17]。

为了解决抗剪强度和临界加速度无法动态变化的问题。刘爱娟等[26]提出了考虑动态临界加速度的永久位移计算法。该方法设定地震时边坡潜在滑动面(Newmark滑块底面)上各质点的黏聚力符合一定概率分布形式,由此各质点具有不同的临界加速度。在地震作用过程中,临界加速度被超过的质点其黏聚力丧失,由此逐步实现潜在滑动面上的总黏聚力以及总临界加速度随地震时程不断减小的过程。采用蒙特卡罗法模拟可能出现的质点黏聚力数值并编制Matlab计算程序,实现了边坡潜在滑动面上黏聚力和边坡临界加速度的动态变化并计算出地震边坡的永久位移。

本文利用动态临界加速度的计算理论,采用实测地震波记录,重新构建永久位移与峰值加速度、阿里亚斯强度、临界加速度之间的回归关系,即考虑动态临界加速度的永久位移预测模型,为区域边坡地震危险性评价提供思路。

1 地震记录选用

选用下载自太平洋地震工程研究中心(PEER)网站的地震加速度实测记录,包含1999年9月16日台湾集集地震、1952年7月21日Kern County地震、1992年4月25日Cape Mendocino地震、1978年9月16日Tabas Iran地震和1986年11月14日Taiwan Smart地震的实测地震加速度时程记录并结合2008年汶川地震部分实测地震波加速度时程数据进行回归分析。在计算过程中,由于地震加速度较小时会出现边坡永久位移为0的情况,所以实际选用时对以上地震记录进行了筛选。

2 回归方法和模型形式

针对不同档次的临界加速度,给定一系列黏聚力平均值c0、黏聚力标准差σ,摩擦角φ、重度γ、坡角α以及滑块厚度值t,在程序中分别求算出每条地震时程记录对应的永久位移DN。利用永久位移、临界加速度、地震峰值加速度或阿里亚斯强度几种数据,回归分析出永久位移预测模型。此外,由于地下水位位置未知,暂不考虑水的作用,黏聚力、摩擦角和重度均按照水位线以上设定。

对于位移预测模型中的变量,一般应包含临界加速度、峰值加速度和永久位移。如果使用的地震参数不是峰值加速度而是阿里亚斯强度,则应包含临界加速度、阿里亚斯强度和永久位移。总结已有文献中位移预测模型的形式,临界加速度与峰值加速度的组合形式可统一表示为式(1)。即因变量永久位移DN或lgDN;自变量为边坡参数和地震动参数,可采取多种形式,如边坡临界加速度ac、地震动峰值加速度PGA或阿里亚斯强度IA,也可以是它们的组合如ac/PGA和lg(ac/PGA)。

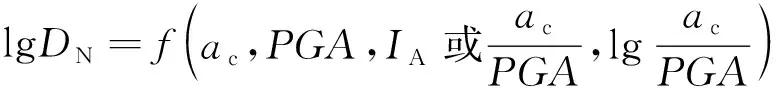
(1)

采用哪些参数作为模型的变量,应采取试算的方法,根据不同变量组合后模型的拟合优度大小进行对比选择。分析已有的位移预测模型表达式,以拟合优度为判断模型优劣的指标时,均显示ac/PGA以及(1-ac/PGA)与lgDN组合呈现较高的拟合优度,所以本文也以这些形式为预测模型的变量表达式。

3 计算结果分析

3.1 永久位移与原永久位移的关系

为了比较考虑动态临界加速度的永久位移值与传统方法计算的永久位移值(原永久位移)的大小关系,本文计算了动态临界加速度方法下的永久位移,并按传统方法计算了临界加速度保持不变时的永久位移,各获得了154组计算结果。比较发现,前者比后者增大约90.7%。永久位移增大的幅度与黏聚力在临界加速度中所占的份额以及地震加速度波形有关,即使具有同样峰值加速度的两列地震波,波形不同,峰值加速度出现的时刻不同,都可能会产生不同大小的永久位移。

3.2 永久位移与临界加速度的关系

为了了解永久位移与临界加速度之间相关性,为预测模型的变量构成提供直观依据,讨论永久位移与临界加速度的关系。选用一组地震动加速度时程曲线,设定5组黏聚力、摩擦角与重度数值,滑块厚度取5 m,选取不同的坡角,从而得到不同的临界加速度值,最后计算出永久位移值。在设定这些数据的时候,应注意参数之间的关联性,比如黏聚力和摩擦角要符合常规的数据大小,不能与实际相差太多。分析结果见图1所示。可以看出,临界加速度ac与DN的关系拟合优度达到0.811 9,而ac与lg(DN)、lg(ac)与lg(DN)的拟合优度只有0.535和0.292 4。需要说明的是,由于黏聚力等参数设定时的不确定性,临界加速度减小过程不一,不同的抗剪强度参数设定比例也会带来一定的偏差,导致拟合优度不如传统方法中仅以临界加速度为变量时高。

图1 永久位移与临界加速度关系图Fig.1 Relation between permanent displacement and critical acceleration

4 预测模型构建

4.1 含峰值加速度的预测模型

根据相关性分析结果,永久位移预测模型的变量选择为lg(DN)、ac、ac/PGA、(1-ac/PGA),其中PGA以amax表示。筛选出可用地震时程记录155条,峰值加速度利用程序进行统计,临界加速度和永久位移利用程序进行计算,最后经统计回归分析,可得式(2)与式(3)两种形式的预测模型。

0.207

(2)

lgDN=3.317-0.963ac+

(3)

公式(2)的拟合优度R2为0.563,公式(3)的拟合优度为0.614,DN单位为 cm,ac单位为g。

从拟合优度大小上来看,本文模型的拟合优度要小于其他文献模型的拟合优度。究其原因,是由于建立模型的时候考虑了临界加速度的动态减小,减小的速度和效果取决于黏聚力标准差的大小、坡体参数的组合形式和地震加速度时程曲线的形状。如果不考虑临界加速度的变化,临界加速度与峰值加速度的关系是设定的几种固定参数,模型只受地震波时程曲线的影响,因此会呈现出拟合优度较大的情况。虽然存在拟合优度相对较小的问题,但在样本数据数量充足的情况下,根据本文模型计算的永久位移结果仍然能够代表地震危险程度的相对高低。与公式(2)相比较,由于拟合优度较大,可选取公式(3)进行区域地震边坡永久位移计算。

4.2 含阿里亚斯强度的预测模型

建立地震动参数和永久位移之间的经验关系时,目前大多数研究成果选取的参数主要是地震动峰值加速度,但若仔细分析可以发现,峰值加速度仅代表某一时刻地震动的最大幅值,难以体现地震波时程的整体能量。阿里亚斯强度则能很好地表现某一时程地震波的能量大小,更符合永久位移的计算原理。

以含阿里亚斯强度的位移预测模型计算永久位移时,需要区域阿里亚斯强度的分布图,目前这部分工作的研究成果不如区域峰值加速度丰富,在无实际地震记录地区预估阿里亚斯强度分布难免不够准确。所以,本文仅做出以阿里亚斯强度为变量的位移预测模型,但不对其结果进行验证。模型的变量构成形式采用Shang-Yu Hsieh[27]分析的最佳组合形式,所得结果见式(4)。

lgDN=3.442+0.547lgIA-0.812ac-

0.735aclgIA±0.381

(4)

式中:DN单位为cm,IA单位为m/s,ac单位为g。拟合优度为0.954。

5 永久位移值大小讨论

永久位移预测模型的理论基础为无限斜坡模型,无限斜坡模型默认了只要地震尚未停止,滑块会在无限长斜坡上一直向下滑行,滑块位移可以一直增大。理论上来讲,位移值可以无限累积增大直至地震时程结束,达到永久位移的最终值。从前文的分析可知,临界加速度是否以动态减小的过程参与计算,很大程度上影响永久位移值的最终结果。

为了对此问题进行讨论,选取溪洛渡至新市镇金沙江两岸边坡作为研究区域,设定地震震级为7.3级,选用四种预测模型分别计算研究区的永久位移并对结果加以对比分析,模型编号从1～4,其中编号1为本文拟合的预测模型公式(3),编号2～4为未考虑滑动面抗剪强度参数减小的预测模型,如表1。分别做出研究区位移分布如图2中(a)～(d)。

表1 四种永久位移预测模型

图2 研究区永久位移分布图Fig.2 Distribution of permanent displacement in the study area

分析这4种位移结果可以看出,由模型1～4计算出的研究区永久位移最大值分别为1 771.46 cm、59.157 5 cm、23.496 3 cm、43.528 7 cm。本文预测模型计算结果最大值达到17.71 m,数值量级为数十米,其他预测模型计算结果最大值达到的量级仅为分米。由动态临界加速度为基础理论计算出的永久位移要远远大于传统方法的计算结果,为了说明本文位移数据的合理性,给出4个滑坡实例[28],以此来判断地震边坡永久位移可能达到的数值量级。

实例1:2006年3月19日,委内瑞拉加拉加斯拉瓜伊拉高速公路1号高架桥附近滑坡的最后一次监测位移值为1.22 m。

实例2:1999年7月23日兰州市西部文昌阁黄土滑坡最后一次观测位移1.22 m。

实例3:1963年10月9日意大利瓦伊昂滑坡监测位移达2.5 m。

实例4:1985年6月12日长江西陵峡新滩滑坡监测位移达7 m。

这些滑坡滑动前的观测位移均超过1 m,由此可以推断地震作用过程中最大滑移量应该达到的量级至少为米才有可能使滑动面贯穿并诱发边坡整体滑动,另外Meehan[25]也通过122个实例发现实测值和预测值之间的差值均超过了1 m。所以从研究区的最大计算位移数值上来看,2、3、4三种传统预测模型计算的永久位移值相对于产生滑坡应达到的位移量偏小,达不到引发滑坡所需的数值,但实际上7.3级地震完全可以诱发大量崩塌或滑坡,例如2013年7级芦山地震诱发了703处崩塌滑坡灾害,2010年玉树7.1级地震极震区诱发崩塌数量约530个,滑坡数量约12个[29]。

需要指出的是,永久位移预测模型假设边坡坡面为无限长,计算中如果滑块永久位移数值超过了边坡坡面的实际长度,并不代表该滑块的实际运移距离等于计算永久位移值。例如坡体基本参数相同、坡角相同而坡高不同的两个边坡,虽然斜坡长度相差很大,在同一列地震波下,其永久位移的计算值是相同的,但实际地震时,滑块在较低坡中已经滑至坡脚并停止滑动,而在较高坡中还未滑至坡底,滑动距离完全不同。无限斜坡模型可以让所有不同规模的边坡处在同一种模型下进行比较,其数值可以作为边坡相对危险性大小的比较,但不能简单地作为滑坡的实际滑动距离。

上述计算位移与实测位移的对比分析也可证明以动态临界加速度为基础拟合的预测模型可以在一定程度上克服普遍存在的预测永久位移量偏小的问题。以此所计算的研究区永久位移结果更加接近滑坡实际位移,能够体现出Newmark滑块理论在无限边坡应用中的实际可能数值,证明该方法具有一定合理性。

6 结论与建议

(1) 动态临界加速度的实现过程与地震时程相对应,不仅在一定程度上解决了地震作用过程中抗剪强度参数变化无法度量的问题,也解决了传统计算法中预测位移比实际位移偏小的问题。

依据动态临界加速度理论并结合多条地震波加速度时程记录,本文构建了分别含有峰值加速度和阿里亚斯强度的两种位移预测模型。采用本文模型计算永久位移,不仅可以解决一直存在的预测位移小于实测位移的问题而且可以更加接近实际状况,在更进一步讨论细化的基础上,还可满足更多的理论应用和工程实际。

(2) 含峰值加速度的以动态临界加速度为基础的永久位移预测模型在存在拟合优度较小的缺点,原因可归结为传统预测模型构建过程中只需要设定一系列临界加速度固定值,由其回归出的模型只受地震波形影响,基本不受位移模型表达式的影响,所以拟合优度很高。而本文方法需要设定多个参数,在很大程度上会造成回归模型的离散性比较大。对于该问题,还需要后续更深入全面地分析与研究。

含阿里亚斯强度的以动态临界加速度为基础的永久位移预测模型的拟合优度比较大,说明阿里亚斯强度具有较好表现地震能量的优点,应在以后的研究中加以重视和研究,逐步由以峰值加速度为主参数过渡至以阿里亚斯强度为主参数,以使地震能量在滑坡中的计算更加准确。

(3) 建议加强地震边坡失稳全过程分析,详细划分滑动阶段如滑面贯通前与贯通后、滑坡体到达坡底前和到达坡底后、同震位移和震后位移等,建立相应的地震边坡失稳或滑动的判断依据和预测模型。