紧聚焦的角向偏振艾里光束产生超分辨光针
刘嘉伟,聂仲泉*
(1.太原理工大学 新型传感器与智能控制教育部与山西省重点实验室,太原 030619;2.太原理工大学 物理与光电工程学院,太原 030619)
引 言
近些年,无衍射超分辨光针因其在激光直写、纳米光刻、高密度磁光存储、超分辨成像和高效粒子操控等领域的广泛应用[1],成为了热门的研究课题。而圆柱矢量光场在无衍射聚焦方面具有独特的优势,其中径向偏振光聚焦后可以在聚焦光场形成很强的纵向成分[2-3]。利用二元相位光学衍射元件能够使聚焦光场的能量重新分布,形成光针。由五环相位滤波器调制的径向偏振贝塞尔-高斯光束经高数值孔径物镜聚焦,形成半峰全宽(full width at half maximum,FWHM)为0.43λ(λ为波长),以及聚焦深度(depth of focus,DOF)为4λ的亚波长纵向偏振光针[4]。同样,利用粒子群优化算法(particle swarm optimization,PSO)优化设计的新型正弦三元混合滤波器,可以调制径向偏振的贝塞尔-高斯光束形成FWHM为0.414λ以及DOF为7.58λ的超分辨纵向偏振光针[5]。以上提到的光针都是由径向偏振光形成,其纵向成分占主导。
同样的,角向偏振光聚焦后可以在聚焦光场形成有着超长的DOF,更有利于应用于激光直写、高密度磁光存储等领域[6-7]。角向偏振光直接聚焦,聚焦光场是中空的暗场[8],与横向偏振光针相关的科研工作较少。而用2π涡旋相位滤波器调制角向偏振光,经高数值孔径物镜聚焦后可以形成纯横向偏振的光针。由2π涡旋相位滤波器和二元相位光学衍射元件调制的角向偏振的贝塞尔-高斯光束聚焦后,形成FWHM为0.40λ以及DOF为6.32λ的无衍射横向偏振光针[9]。贝塞尔-高斯光束具有无衍射和自愈合的特性,成为研究者们设计优化光针的热门选择。艾里光束不仅具备无衍射和自愈合的特性,而且拥有独特的自加速性质,可以应用到粒子操控等1维领域,而其它光束只能应用到更高维的领域。
本文中利用多环涡旋相位滤波器调制角向偏振的艾里光束,经过高数值孔径物镜聚焦后形成超长无衍射超分辨横向偏振光针。在仿真中,设置艾里光束的指数衰减因子a0=0.03,主环半径r0=2.8mm,比例因子w=0.03mm。通过PSO算法设计优化了不同的滤波器,其中五环滤波器可以形成FWHM是0.395λ与DOF是37.432λ的光针。进一步利用斯托克斯参量分析聚焦光场的偏振分布,得出聚焦光场在径向偏振与角向偏振之间交替变化,且光束中心奇异点消失,证明实现了横向偏振的亮场分布。
1 理 论
1.1 角向偏振艾里光束的紧聚焦特性分析
如图1所示,角向偏振的艾里光束沿z轴水平入射,通过高数值孔径(numerical aperture,NA)物镜聚焦,根据理查德-沃夫矢量衍射理论,其聚焦光场附近的电场分布可表示为[10-11]:

Fig.1 Schematic setup to generate the super-resolution and transversally polarized light needle
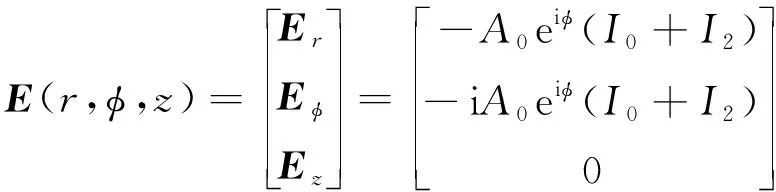
(1)
式中,Er,Eφ,Ez分别表示聚焦光场在圆柱坐标系中r,φ,z方向的分量,A0是常数,仿真中可以忽略。
exp(ikzcosθ)Jn(krsinθ)dθ
(2)
式中,α=arcsindNA/n0是物镜的最大半会聚角,n0是空间的折射系数,k=2π/λ是真空中的波矢,λ是入射光的波长,Jn是第1类n阶贝塞尔函数,l0(θ)是角向偏振艾里光束的切趾函数[12],可表示为:

(3)
式中,A(·)表示艾里函数,r1可以设置r1=fsinθ,f是聚焦物镜的焦距,a0>0是指数衰减因子。强度最高的艾里环位于r0-w处,它的FWHM近似为2.28w[13]。
1.2 角向偏振艾里光束的紧聚焦实验方法
如图2所示,艾里光束可以利用液晶空间光调制器(spatial light modulator,SLM)加载空间相位产生[14]。首先,激光光源发射一束线偏振激光(λ=532nm),通过激光扩束镜扩展,以合适的角度入射到加载了艾里空间相位的反射式SLM的液晶面板。接着,将经相位调制后的线偏振激光反射到傅里叶薄透镜。经过傅里叶变换,在透镜的焦平面,产生了线偏振艾里光束。将一个环形孔径放置在透镜焦平面,过滤光束的低频成分。之后,线偏振艾里光束经零阶涡旋波片(LBTEK,VR1-532)调制生成角向偏振艾里光束。该波片并不会改变艾里光束的光强分布。最后,角向偏振艾里光束通过高数值孔径物镜聚焦,在聚焦平面生成超长无衍射超分辨的横向光针。
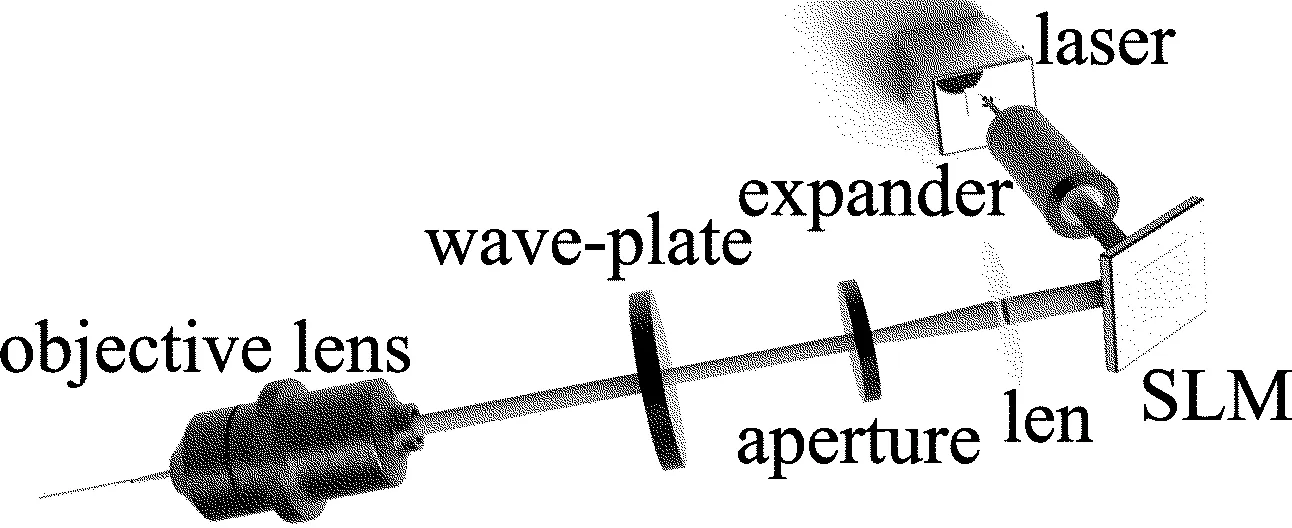
Fig.2 Experimental method to generate an azimuthally polarized Airy beam
2 仿真结果
2.1 指数衰减因子a0、主环半径r0和比例因子w对入射艾里光束的影响
入射艾里光束的各项参量,影响着紧聚焦后超分辨横向偏振光针的性质[15-16]。因而通过仿真模拟,探究指数衰减因子a0、主环半径r0和比例因子w对入射艾里光束的影响有着重要意义。首先,设置聚焦物镜的焦距f=3mm,主环半径r0=2.8mm,比例因子w=0.03mm,指数衰减因子a0分别为0.01,0.1,1。图3a~图3c所示。是不同的指数衰减因子a0所对应的入射场光强的分布情况。在a0=0.01时,艾里光束的能量散布在其主瓣和诸多旁瓣上;在a0=1时,艾里光束的能量只集中分布在主瓣上,光场变为甜甜圈的形状;而a0=0.1时,艾里光束的能量主要分布在主瓣上,少量分布在旁瓣上,是一种中间态。接着,设置聚焦物镜的焦距f=3mm,指数衰减因子a0=0.25,比例因子w=0.03mm,主环半径r0分别为2mm,2.5mm,3mm。图3d~图3f所示是不同的主环半径r0所对应的入射场光强的分布情况。从图3d~图3f可知,艾里光束的主瓣和旁瓣能量分布比例并无变化,主瓣的直径从2mm变化到3mm。最后,设置聚焦物镜的焦距f=3mm,指数衰减因子a0=0.25,主环半径r0=2.8mm,比例因子w分别为0.05mm,0.1mm,0.5mm。如图3g~图3i所示,艾里光束的主瓣和旁瓣能量分布比例并无变化,主瓣的直径也保持一致,而主瓣的宽度从0.05mm变化到0.5mm。
综上所述,对于艾里光束,指数衰减因子a0影响其光场能量在主瓣和旁瓣的分布比例,主环半径r0影响其主瓣的直径,比例因子w影响其主瓣的宽度。为了提升紧聚焦后产生的超分辨光针的DOF并压缩其FWHM,在之后的仿真实验中,设置聚焦物镜的焦距f=3mm,指数衰减因子a0=0.03,主环半径r0=2.8mm,比例因子w=0.03mm。
2.2 多环涡旋相位滤波器对紧聚焦性质的影响
如图4a、图4b所示,未经调制的角向偏振光紧聚焦后,在聚焦光场只存在角向成分,径向成分和轴向成分为零,光场呈现中空分布。如图4c所示,在实验中生成了紧聚焦后未经调制的角向偏振光[17]。根据(1)式,经涡旋相位滤波器调制的角向偏振光紧聚焦后[18],在聚焦光场产生径向成分。这是因为偏振分布和相位分布之间有联系,入射光相位的改变会导致聚焦光场的偏振发生改变。如图4d~图4e所示,经调制的角向偏振光紧聚焦后,由于同时存在角向成分和径向成分,中心的偏振奇异点消失,光场的中空分布消失。如图4f所示,是经调制的角向偏振光紧聚焦后的实验结果。
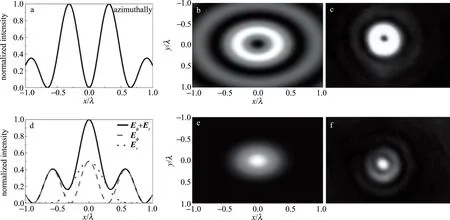
Fig.4 a~c—the normalized intensity profiles,normalized intensity patterns in the x-y planes and experimental results of unmodulated azimuthally polarized beam by tightly focusing,respectively d~f—the normalized intensity profiles,normalized intensity patterns in the x-y planes and experimental results of modulated azimuthally polarized beam by tightly focusing,respectively
为了实现超长无衍射超分辨横向偏振艾里光针,作者设计了N环涡旋相位滤波器,可压缩沿r方向的旁瓣并延长z方向的聚焦深度。如图1所示,角向偏振的艾里光束沿z轴水平入射,经由N环涡旋相位滤波器调制和高数值孔径物镜聚焦,该滤波器由不同透过率f(θ)和不同相位φ(θ)的同心环组成,每个环对应的径向位置可以表示为rt=sinθt/dNA(相对于光瞳的归一化半径)。经调制后聚焦场的In可重新表示为:
exp(ikzcosθ)Jn(krsinθ)dθ
(4)
式中,环形滤波器的环数t=1,2,3,…,N;θt=arcsinrt×dNA/n0是物镜的半会聚角(θ0=0,θN=θmax=arcsindNA/n0)。在仿真中,设定入射光的波长λ=532nm,物镜的数值孔径为0.95,空间的折射系数n0=1。作者使用了PSO算法,该算法是一种基于群体的启发式优化算法,由肯尼迪和艾伯哈特提出。PSO算法先要设置一个随机的解群空间,然后搜索最优解,每个解都是解群空间里面的一个粒子,每个粒子都有自己的位置矢量和速度矢量。设置合适的DOF和FWHM作为结束搜索的特定条件,设计优化了四环和五环涡旋相位滤波器每个环的径向位置rt,得到了超长无衍射超分辨横向偏振艾里光针。
如图5a~图5c所示,分别是当涡旋相位滤波器的N为1,4,5时,经过调制的角向偏振的艾里光束聚焦后,总场沿着z轴方向的分布情况。可以看出,生成的横向艾里光针沿着z轴方向分布均匀,在较长范围没有发生衍射。如图5d和表1所示,当N=4时,艾里光针的DOF大约是37.743λ,是N=1时艾里光针DOF的3.687倍,这表明N=4时,涡旋相位滤波器可以延长z方向的聚焦深度,其纵横比达到94.760。当N=5时,艾里光针的DOF大约是37.432λ,与N=4时光针的DOF相比并没有太大变化,但是分布的均匀性得到很大提升。如图5e和表1所示,当N分别为1,4,5时,艾里光针的FWHM几乎保持不变,大约是0.398λ。当入射光的波长λ=532nm、物镜的dNA=0.95时,光场的阿贝衍射极限是0.5λ/dNA=0.53λ,因此生成了超长无衍射超分辨横向偏振艾里光针。
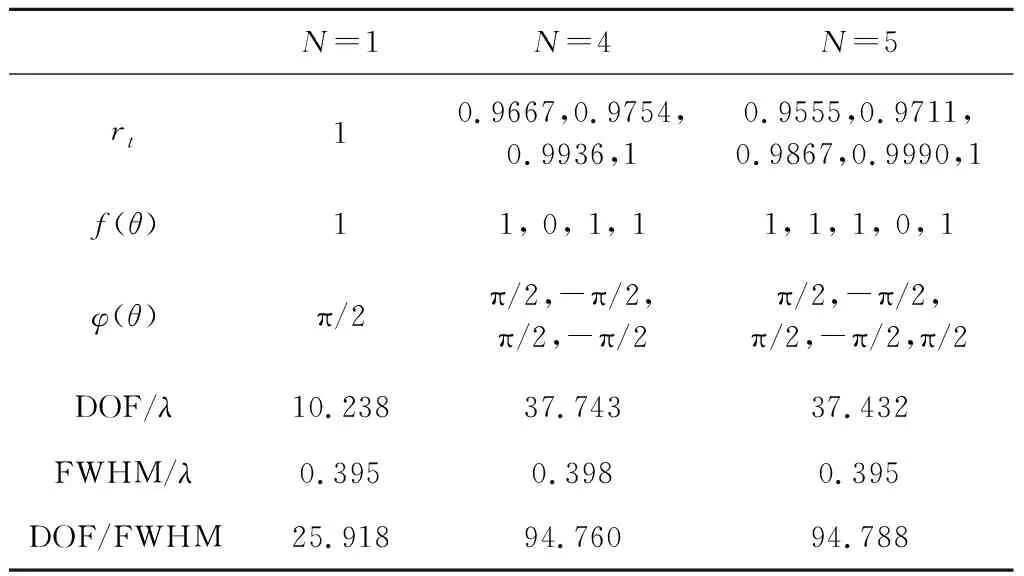
Table 1 The essential parameters of the multi-loop vortex phase filter and properties of airy light needle

Fig.5 a~c—the normalized intensity patterns of the light needle in the y-z planes for N=1,4 and 5,respectively d~e—the depth of focus and full width at half maximum of transversally polarized Airy light needle for N=1,4 and 5,respectively
2.3 通过斯托克斯偏振参量分析紧聚焦光场的偏振分布
可以通过分析斯托克斯参量来研究横向偏振艾里光针的偏振分布详情。局部偏振椭圆的方位角ψ和椭圆率tanχ可以表示为[19-20]:

(5)
式中,arg()表示复角,I0*表示I0的复共轭。
图6a所示是局部偏振椭圆在焦点处延x轴方向的椭圆率分布情况。可以发现,椭圆率在空间上是变化的。在聚焦平面中心,椭圆率是1,表示这里是右旋圆偏振光。沿着径向方向,椭圆率从1变化到-1,偏振从右旋圆偏振变化到左旋圆偏振。如图6b所示,这些小短线是在聚焦平面内局部偏振椭圆长轴的方向,其在径向方向和角向方向间交替变化,呈现轴对称分布。椭圆率从1变化到-1的区域是径向分布,反之是角向分布。在变化的边界区域,椭圆率是±1,这里是偏振的奇异点,属于圆偏振,方位角ψ无法计算[21]。总之,通过斯托克斯偏振参量分析了紧聚焦光场的偏振分布,光场的偏振在空间上呈现径向偏振与角向偏振的交替变化,且中心奇点消失,其区域大小约为0.4λ,证明利用多环形涡旋滤波器实现了横向偏振的超分辨光场分布。

Fig.6 a—cross section of the ellipticity of local polarization ellipses in the x-z planes b—the azimuthal angle distribution in the focal plane
3 结 论
利用PSO算法优化设计了多环涡旋相位滤波器调制角向偏振艾里光束,经高数值孔径物镜聚焦后生成了超长无衍射超分辨横向偏振光针。其中,五环涡旋相位滤波器的优化效果最好,压缩沿横向方向的旁瓣并延长轴向方向的聚焦深度,并且光场分布十分均匀,光针的FWHM大约是0.395λ,低于阿贝衍射极限,DOF大约是37.432λ,纵横比达到94.788。通过斯托克斯偏振参量分析了紧聚焦光场的偏振分布,光场的偏振在空间上呈现径向偏振与角向偏振的交替变化,其中心奇点消失,为亮的右旋圆偏振光。在实际应用中,通过SLM能实现作者编码的多环涡旋相位滤波器。横向偏振的超分辨光针在激光直写、纳米光子学、高密度磁光存储、超分辨成像和粒子操控等领域具有广阔的应用前景。需要注意的是,该滤波器生成的超长无衍射超分辨横向偏振光针的横向旁瓣较大,不适于广泛应用,之后需要扩展滤波器的调制维度,减少横向旁瓣。

