钢纤维掺量对混凝土抗拉疲劳性能影响的试验研究

张志彪，郭蒙蒙，朱茹琳，冯仲仁

(1.安徽省水利水电勘测设计院， 安徽 合肥 230000； 2.安徽省高路建设有限公司；3.安徽保利房地产开发有限公司；4.武汉理工大学 土木工程与建筑学院)

1 引言

当前混凝土构件承受的荷载类型越来越复杂，钢纤维混凝土凭借良好的力学性能越来越多地被使用，但钢纤维混凝土(SFRC)构件的疲劳及损伤性能研究已不能满足工程项目的需求。

近些年各国学者对SFRC疲劳问题主要做了以下研究。S.Goel和S.P.Singh通过普通混凝土梁及SFRC梁弯曲疲劳试验，研究了钢纤维对试验梁疲劳性能的影响；Germano F通过2种钢纤维体积率及3个不同荷载水平试验，表明钢纤维可改善混凝土的疲劳寿命；Parvez Ahasn通过12根不同钢纤维含量的钢筋混凝土梁弯曲疲劳试验，表明SFRC构件大大提高了抗疲劳性能和抗裂纹扩展性能，降低了梁的跨中挠度，减小了受拉纵筋应力水平；Ruiz Gonzalo通过4种加载频率的SFRC立方体试块受压疲劳试验，表明钢纤维通过抑制低频循环加载作用时裂纹扩展速率，提高了混凝土疲劳性能；MG Girish设计了SFRC在循环荷载作用下的疲劳试验，得到了相关的S-N曲线；杨润年通过SFRC梁弯曲疲劳试验，得到疲劳荷载作用下的本构模型及损伤演化模型；高丹盈通过8根钢纤维高强混凝土梁疲劳试验，表明掺入钢纤维可以抑制裂纹的扩展；方志通过不同钢纤维掺入量SFRC单轴等幅受压疲劳试验，得到体积率为1.5%和3%时试件剪切破坏，表明钢纤维改善了混凝土的疲劳性能；侯蔚峰通过多种钢纤维掺入量的SFRC梁弯曲静载试验以及循环往复加载试验，研究了SFRC梁的弯曲疲劳特性；李书群通过不同应力比下的SFRC梁的弯曲疲劳试验，作出不同应力比下的S-N曲线；石北啸通过不同钢纤维体积率的混凝土疲劳试验，表明钢纤维体积率在某一临界值以内时，SFRC的疲劳性能随着钢纤维体积率的增加而明显提高；冯仲仁等的研究结果表明:钢纤维混凝土的疲劳性能明显高于普通混凝土,其疲劳强度较普通混凝土提高20%左右。

该文设计SFRC试件的单轴疲劳试验，研究钢纤维合理体积率取值，并推导考虑钢纤维体积率的SFRC疲劳方程。

2 试验状况

2.1 试件设计

浇筑试件选取设计强度等级C30的普通混凝土，掺入不同体积率的钢纤维(0，0.5%，1.0%，1.5%)，SFRC材料的配合比为：水泥∶水∶粉煤灰∶河砂∶碎石=1∶0.41∶0.27∶1.84∶2.36。其他要求见表1。

表1 SFRC材料要求

试验试件为长×宽×高= 300 mm×100 mm×100 mm的棱柱体，见图1，中间部分为试验实际测试部位。在试件两端分别预埋一根φ14的钢筋，伸入端部100 mm，控制两端预埋钢筋严格对中，浇筑成型的SFRC试件见图2。SFRC试件表面粘贴应变计，用以测量循环加载时试件的应变。同一批SFRC浇筑5个边长15 cm的标准立方体试块，用来检测同批次棱柱体试件是否满足要求。

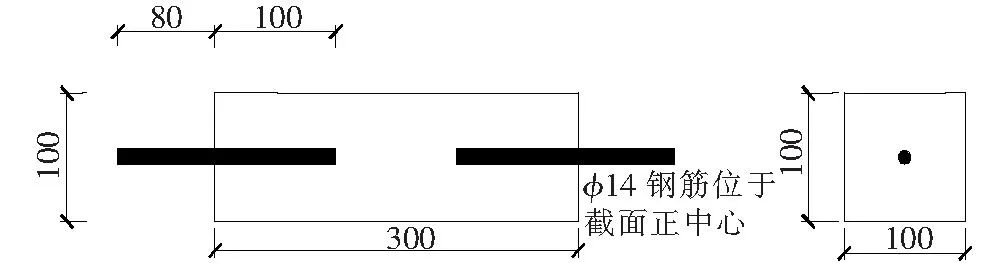
图1 SFRC试件尺寸(单位：mm)

图2 SFRC试件

2.2 试验设备

疲劳试验采用电液伺服万能材料试验机加载装置，量测采用DH5908动应变测试系统。疲劳试验机配套计算机动态采集荷载和变形，DH5908动态应变测试系统采集应变。

试件安装形式见图3。

图3 SFRC试件安装

2.3 试验加载工况

单轴疲劳试验采用4种钢纤维体积率，8个应力水平正弦加载，进行单轴受拉循环疲劳试验，加载工况见表2。

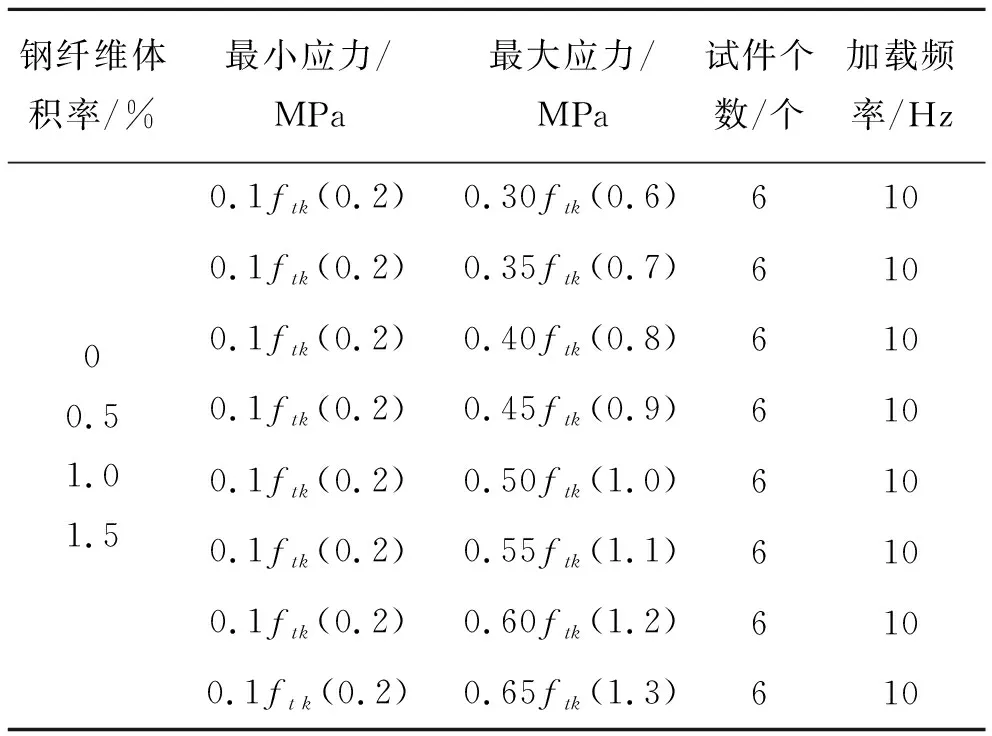
表2 单轴疲劳试验加载工况

试验试件数量为每一应力水平下对6个试件进行试验，初步试验结束后复核试件个数，对不满足最小试验个数的应力水平进行补测。为研究不同钢纤维体积率的混凝土疲劳性能，试验荷载最小应力水平应取0.1ftk即0.2 MPa，最大应力水平由0.6 MPa递加至1.3 MPa，单次递增0.1 MPa。若试件在达到1×106次循环周期后没有破坏，则认为在此加载工况作用下，试件具有无限疲劳寿命。

3 试验结果分析

3.1 试件破坏形态

图4为SFRC试件破坏断面SEM扫描电镜图，图5为SFRC试件破坏形态。

图4 SEM扫描电镜图

图5 试件破坏形态

由图4、5可以看出：SFRC试件在疲劳荷载作用下，沿试件中间位置发生断裂破坏。破坏发生前几秒钟，试件表面出现细微裂纹，随之发生断裂破坏，伴随有钝音。断裂面不规整，断裂面两侧混凝土无明显破坏损伤，断裂的形式主要是粗骨料拉断破坏及粗骨料与水泥砂浆界面分离破坏，钢纤维基本都是拔出剥离，极少断裂破坏。

3.2 试验结果

由试验测得的SFRC试件在各应力幅值下的疲劳寿命见表4。

表3 单轴疲劳试验结果

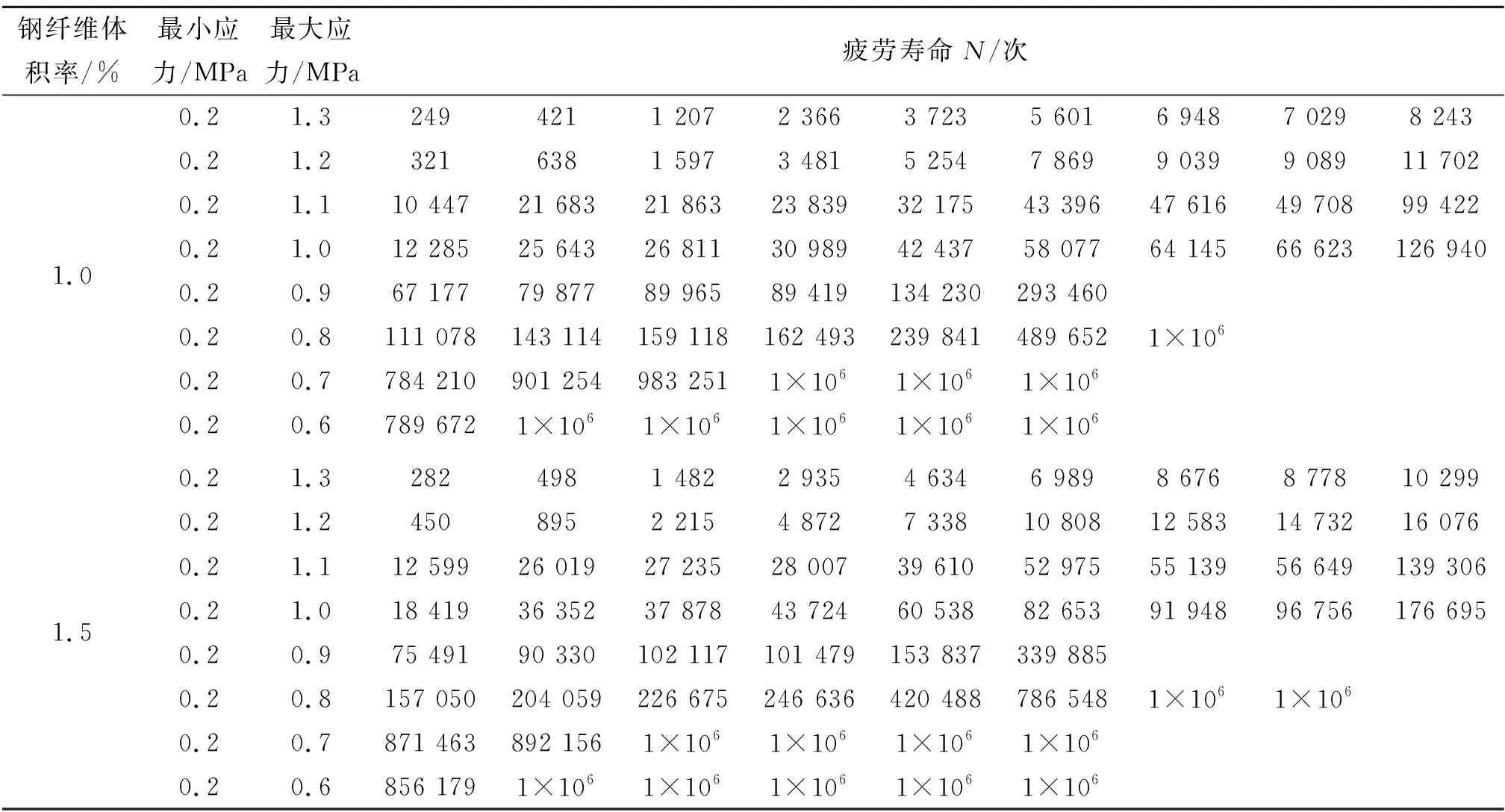
续表3

3.3 结果分析

由疲劳试验数据分析可知：SFRC试件在最大应力水平为0.6 MPa时，开始发生疲劳破坏；当最大应力水平为0.8～0.9 MPa时，SFRC试件开始发生稳定破坏；而最大应力水平为0.6 MPa以下时，SFRC试件才出现无限疲劳寿命。

鉴于混凝土材料自身的强离散性，将试验数据作回归处理，利用多项式拟合，得出形如式(1)的一阶指数函数疲劳寿命表达式(S-N曲线)。

Smax=α-β(1-R)lgN

(1)

式中：Smax为最大应力水平，Smax=σmax/f，其中f为SFRC材料的静载抗拉强度，以普通混凝土的抗拉强度值1.25倍计；α，β为材料常数，由试验拟合得到；R为应力比，R=σmin/σmax；N为疲劳寿命。

将试验数据作回归分析，用“最小二乘法”对处理后的试验数据作指数函数形式的多项式拟合，得到循环荷载最大应力水平与加载循环次数对数值之间的多项式。

钢纤维体积率等于0%，S-N表达式为：

Smax=0.107 6+0.052 8(1-R)lgN

(2)

R2=0.966 9，σ=0.010 5

钢纤维体积率等于0.5%，S-N表达式：

Smax=0.105 4+0.052 2(1-R)lgN

(3)

R2=0.959 2，σ=0.011 3

钢纤维体积率等于1.0%，S-N表达式：

Smax=0.098 1+0.053 2(1-R)lgN

(4)

R2=0.952 6，σ=0.012 4

钢纤维体积率等于1.5%，S-N表达式：

Smax=0.096 0+0.056 3(1-R)lgN

(5)

R2=0.946 2，σ=0.013 1

使用Matlab对试验数据进行回归拟合，得到不同钢纤维体积率的S-N曲线指数函数表达式的相关系数R2为95%左右，即拟合得到一阶多项式与试验结果符合程度高。各钢纤维体积率试件对应疲劳寿命S-N曲线和S-lgN曲线见图6、7。

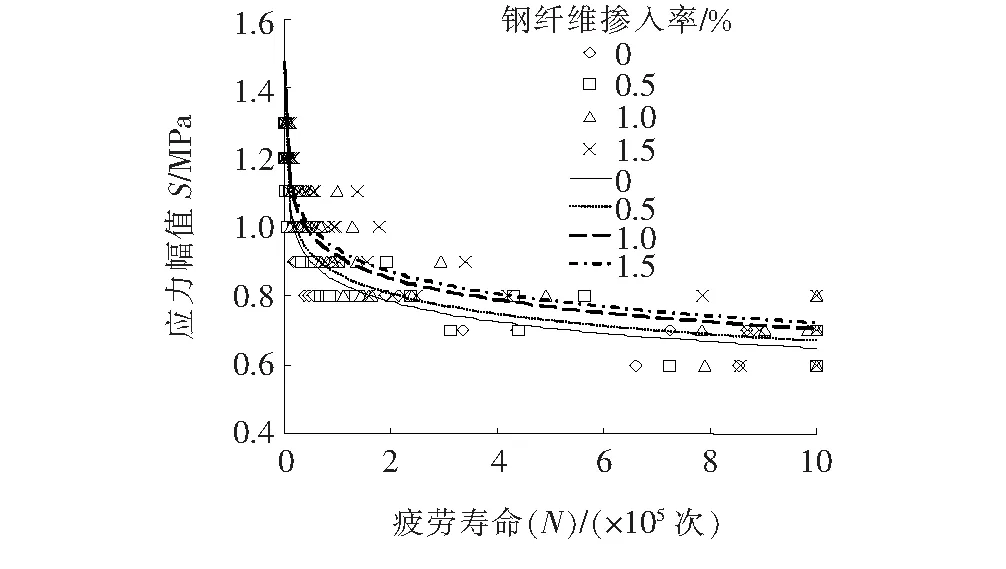
图6 疲劳寿命S-N曲线

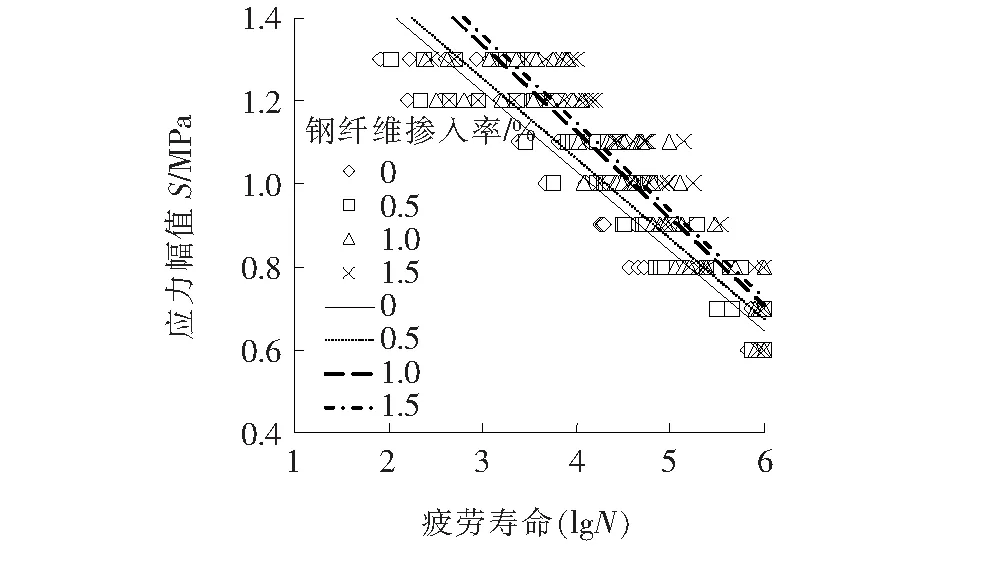
图7 疲劳寿命S-lgN曲线

由S-N曲线可得不同钢纤维体积率的SFRC试件疲劳强度及其与普通混凝土试件的增幅关系，见表4。

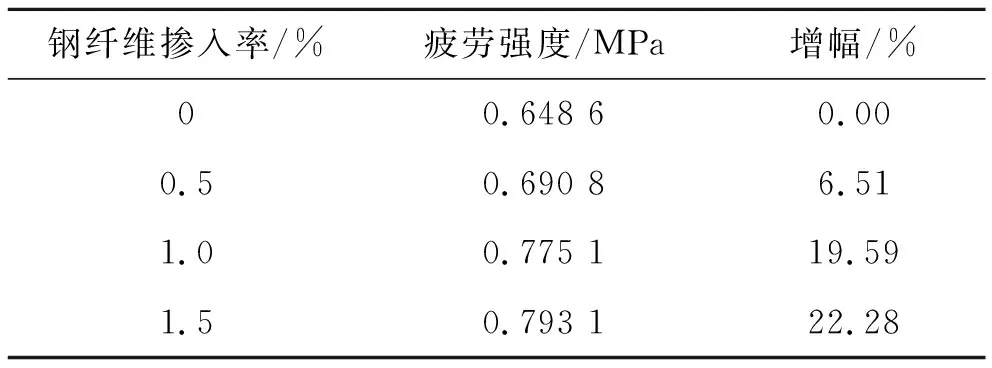
表4 疲劳强度对比

由表4可以看出：掺入钢纤维后试件的疲劳强度明显增大，但在钢纤维体积率超过1.0%后，SFRC材料的疲劳强度增幅减弱。

3.4 疲劳方程

SFRC材料的疲劳特性与钢纤维体积率、长径比即Vflf/df特征参数密切相关，因此将考虑钢纤维体积率为影响因素的疲劳表达式参照SFRC规范推导如下。

SFRC材料的疲劳抗拉强度标准值：

fftk，f=ftk，f(1+αeVflf/df)

(6)

式中：fftk，f为SFRC材料疲劳抗拉强度标准值；ftk，f为普通混凝土疲劳抗拉强度标准值；αe为影响系数，由试验确定；Vf为钢纤维体积率；lf/df为钢纤维长径比。

SFRC材料的抗拉疲劳应力：

Scf=S(1+αeVflf/df)

(7)

式中：Scf为SFRC材料抗拉疲劳应力水平；S为普通混凝土抗拉疲劳应力水平。

根据试验数据拟合确定αe=0.074 1，并结合式(2)、(6)可得考虑钢纤维体积率的SFRC的疲劳方程：

Scf=[0.107 6+0.052 8(1-R)lgN]·(1+0.074 1Vflf/df)

(8)

R2=0.966 9，σ=0.010 5

4 结论

利用电液伺服材料试验机，通过4种钢纤维体积率、每种8个应力水平的SFRC试件单轴疲劳试验研究，得到以下结论：

(1) 钢纤维混凝土在疲劳荷载作用下，钢纤维体积率为0.5%、1.0%、1.5%时，疲劳强度较普通混凝土分别提高6.51%、19.59%、22.28%，可以看出掺入钢纤维后试件的疲劳强度明显增大，但在钢纤维体积率超过1.0%后，SFRC材料的疲劳强度增幅明显减弱。因此认为SFRC构件疲劳荷载作用下的合理钢纤维体积率可取1.0%。

(2) 得出考虑钢纤维体积率的SFRC材料疲劳方程：Scf=(0.107 6+0.052 8(1-R)lgN)·(1+0.074 1Vflf/df)。