桥梁墩台顺桥向水平力分配计算

李学有，李顺波

(中交第二公路勘察设计研究院有限公司，湖北 武汉 430056)

1 前言

近年来，随着中国交通运输事业的快速发展，桥梁建造技术不断进步。其中，中小跨径连续梁桥、连续桥面简支梁桥、多跨连续简支梁桥的应用极为普遍，由于该类桥梁量大面广，对其经济性和安全性的平衡，一直是桥梁工程师的探索目标。

梁式桥的上部结构，多采用相关的通用标准图集，鉴于有限元分析软件的日益成熟，计算软件可提供一站式分析功能，计算结果相对明确。而下部结构，由于地质条件、桥墩高度、桥梁跨径等因素，较难采用通用标准图集，一般均需针对具体项目进行具体计算分析。

该文基于刚度集成法，考虑活动支座的非线性影响和不同作用的加载顺序，提出墩台顺桥向水平力分配计算的非线性分析方法。

2 墩台顺桥向水平力计算方法讨论

梁式桥下部结构一般采用柔性桥墩，其计算分析的要点是墩台顺桥向水平力的分配计算。许多学者对此进行了大量的分析研究，提出的方法有三推力方程法、一次迭代法、柔度系数法、刚度集成法等。

总体而言，桥梁顺桥向水平力包括汽车制动力、温度作用、上部结构梁体收缩徐变引起的水平力等。具体计算过程中，上部结构梁体收缩徐变引起的水平力一般等效为整体降温处理。因此，墩台顺桥向水平力分配计算简化为汽车制动力和温度作用(含升温和降温)的水平力计算。

梁式桥一般在一联之内设置活动支座(盆式活动支座或四氟滑板橡胶支座等)，当活动支座分配的纵向水平力大于摩阻力时，设置活动支座的墩台不再参与纵向水平力分配。因此，设置活动支座的桥梁墩台水平力计算，实质是一个非线性分析过程。

虽然，针对制动力和温度作用的水平力计算，学者们提出了较多的分析方法，但是桥梁下部结构水平力计算，通常采用以下简化方法：

(1) 不考虑活动支座的非线性影响，纵向水平力在不设置活动支座的桥墩间分配，将非线性问题转化为线性问题。

(2) 由于采用第(1)项假定，当不同类型的纵向水平力共同作用时，将计算结果线性相加，未考虑非线性问题的作用效应与作用加载顺序相关。

3 墩台集成刚度计算

目前已提出的三推力方程法、一次迭代法、柔度系数法、刚度集成法等方法，在工程设计中应用最为普遍的是刚度集成法。

刚度集成法的原理，首先是计算每个墩台的集成刚度，其次是根据各墩台集成刚度的比例，分配墩台顶部水平力。下面简述墩台集成刚度的计算方法。

3.1 支座刚度计算

现阶段，桥梁使用较多的支座是板式橡胶支座和盆式支座。

(1) 板式橡胶支座刚度

板式橡胶支座刚度的计算，可参考JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》8.7节的规定，支座刚度按下式计算：

(1)

式中:n为墩台顶部支座个数；Ge为支座剪变模量；A为支座平面面积；t为支座橡胶层总厚度。

(2) 盆式支座刚度

固定盆式支座的支座刚度，在合理的支座受力范围内，可近似按无穷大考虑。

活动盆式支座的支座刚度，可参考JTG/T B02-01-2008《公路桥梁抗震设计细则》6.3.7条规定，支座刚度按下式计算：

(2)

(3)

式中:μd为摩擦系数，一般取0.02；R为支座承担的上部结构自重；xy为盆式支座屈服位移，一般取0.002～0.005 m。

3.2 墩台刚度计算

(1) 桥台刚度计算

总体而言，目前桥梁设计中应用较为普遍的重力式桥台、肋板桥台等，台身刚度可近似按无穷大考虑。至于柔性桥台，可参考文献[4]所述简化方法进行台身刚度计算。

(2) 桥墩刚度计算

桥墩刚度的计算方法，其焦点在于桥墩顶部边界条件的确定。文献[8]认为，上部结构对于桥墩具有一定的约束，提出考虑墩顶弹性嵌固的刚度耦合模型。一般而言，传统的刚度集成法不考虑上部结构对于桥墩的约束作用，墩顶按自由边界考虑，在文献[4]第3.2节对此进行过详细论述。

桥墩顶部边界条件，影响的是单个桥墩的刚度数值，并不影响刚度集成法的计算原理。有关桥墩刚度的简化计算方法，可参考相关文献[5,8]。

(3) 墩台刚度计算的有限元方法

自动上传存储：录播完成后，视频会自动存储在服务器的云端。师生在校内可以登录校内的网址进行查看，输入注册后的用户名和密码下载录制的视频。

墩台刚度计算的简化计算方法，相关文献已有较多论述。鉴于有限元计算方法的不断普及，墩台刚度可通过有限元软件进行计算。

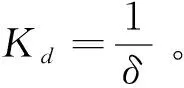
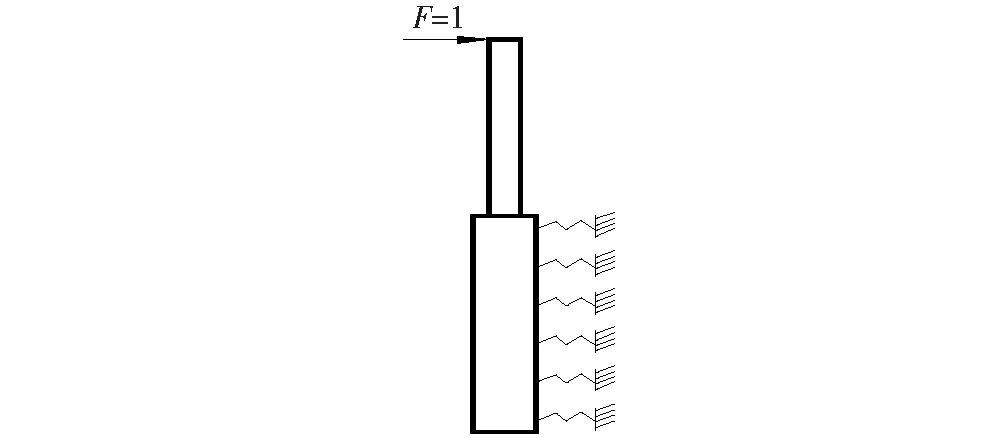
图1 桥墩刚度计算示意图

3.3 集成刚度计算

针对单个墩台而言，支座刚度与墩台刚度是串联关系，则墩台集成刚度Ki为:

(4)

针对某一联桥梁而言，各墩台刚度是并联关系，则整联桥梁抗推刚度为：

K=∑Ki

(5)

4 水平力分配计算方法

在前述集成刚度计算的基础上，考虑活动支座的非线性影响和作用加载顺序，给出桥梁墩台顺桥向水平力分配计算的非线性分析方法。

4.1 制动力作用下水平力计算

由于存在活动支座，需要判断活动支座分配水平力是否大于摩阻力，因此，制动力的分配计算是反复迭代的过程，其迭代步骤为：

(1) 初估迭代初值：根据各墩台刚度，按比例分配制动力F，则墩台i分配的制动力Fzi为：

(6)

(2) 活动支座水平力判断调整：

① 若各活动支座分配水平力Fzj不大于摩阻力μR，转至(4)；② 若活动支座分配水平力Fzj大于摩阻力μR，活动支座水平力取为μR，对应墩台刚度Kj设置为0，大于摩阻力的水平力在其他墩台间分配，即：

Fzj=μR，Kj=0

(7)

Ft=∑(Fj-μR)

(8)

式中：Ft为再分配水平力。

K=∑Ki(i=1，2，…，m)

(9)

(10)

(3) 计算各墩台分配的水平力：

Fzi=Fzi+Fzit(i=1，2，…，m)

(11)

并转至(2)。

(4) 确定各墩台分配水平力为Fzi。

4.2 温度作用下水平力计算

与制动力分配计算类似，温度作用引起的水平力计算也是反复迭代的过程，其迭代步骤为：

(1) 初定温度零点：

(12)

式中：α为线膨胀系数；t为温度差值；Li为i号墩台距离桥梁左端的距离。

(2) 初估迭代初值：根据初定的温度零点，计算各墩台的水平力Fwi：

Fwi=Ki·α·(Li-L0)·t

(13)

(3) 活动支座水平力判断调整：

① 若各活动支座分配水平力Fwj不大于摩阻力μR，转至(5)；② 若活动支座分配水平力Fwj大于摩阻力μR，活动支座水平力取为μR，即Fwj=μR。

(4) 重新确定温度零点和墩台水平力：

(14)

Fwi=Ki·α·(Li-L0)·t

(15)

转至(3)。

(5) 确定各墩台分配水平力为Fwi。

4.3 作用组合下水平力计算

如前所述，作用组合下水平力计算主要涉及制动力和温度作用的组合。由于活动支座的非线性影响，作用组合结果，不是简单地将各作用的计算结果线性相加，而是需要考虑作用的加载顺序。

4.3.1 “温度力+制动力”作用

“温度力+制动力”作用，表示桥梁墩台先承受温度作用，然后再分配制动力。其计算步骤为：

(1) 用温度作用迭代计算程序，得到温度作用下各墩台分配水平力Fwi。

(2) 初估迭代初值：根据各墩台刚度，按比例分配制动力F，则墩台i分配的制动力Fzi按式(6)计算。然后以Fi=Fwi+Fzi作为迭代初值。

(3) 活动支座水平力判断调整：

① 若各活动支座分配水平力Fj不大于摩阻力μR，转至(4)；② 若活动支座分配水平力Fj大于摩阻力μR，活动支座水平力取为μR，对应墩台刚度Kj设置为0，大于摩阻力的水平力在其他墩台间分配，即：

Fj=μR，Kj=0

(16)

Ft=∑(Fj-μR)

(17)

K=∑Ki(i=1，2，…，m)

(18)

(19)

(4) 计算各墩台分配的水平力：

Fi=Fi+Fit(i=1，2，…，m)

(20)

并转至(3)。

(5) 确定各墩台分配水平力为Fi。

4.3.2 “制动力+温度力”作用

“制动力+温度力”作用，表示桥梁墩台先分配制动力，然后再承受温度作用。此种工况在现实情况中较少出现，为了阐述不同加载顺序对水平力分配结果的影响，该文给出定量分析算法，其计算步骤为：

(1) 调用制动力迭代计算程序，得到制动力作用下各墩台分配水平力Fzi。

(2) 初定温度零点和迭代初值：

温度零点按式(12)计算。根据初定的温度零点，计算各墩台的水平力Fwi。以Fi=Fzi+Fwi作为迭代初值。

(3) 活动支座水平力判断调整：

① 若各活动支座分配水平力Fj不大于摩阻力μR，转至(5)；② 若活动支座分配水平力Fj大于摩阻力μR，活动支座水平力取为μR，即Fj=μR。

(4) 重新确定温度零点和墩台水平力：

(21)

Fi=Fzi+Ki·α·(Li-L0)·t

(22)

转至(3)。

(5) 确定各墩台分配水平力为Fi。

5 算例

某桥梁上部结构采用30 m简支T梁，5孔一联，每跨T梁横向5片(图2)。桥台设置一排聚四氟乙烯滑板支座，规格为250 mm×350 mm×59 mm；桥墩设置两排板式橡胶支座，规格为250 mm×350 mm×57 mm。

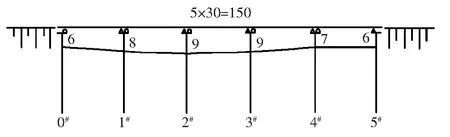
图2 桥梁立面图(单位：m)

桥梁制动力取103.7 kN，整体升温20 ℃，整体降温55 ℃(考虑收缩徐变)。

参考部版通用图，简支T梁梁端恒载反力取值为2 830.0 kN；滑板支座摩阻系数取0.06，则活动支座摩阻力为169.8 kN。

桥台台身刚度近似按无穷大考虑，则桥台刚度采用支座刚度，数值为10 417.0 kN/m。各墩台刚度计算结果见表1。

表1 墩台刚度计算结果

根据上述桥梁参数，采用该文提出的水平力分配计算方法，计算墩台水平力，计算结果如表2所示；同时表3为文献[8]对应计算结果。

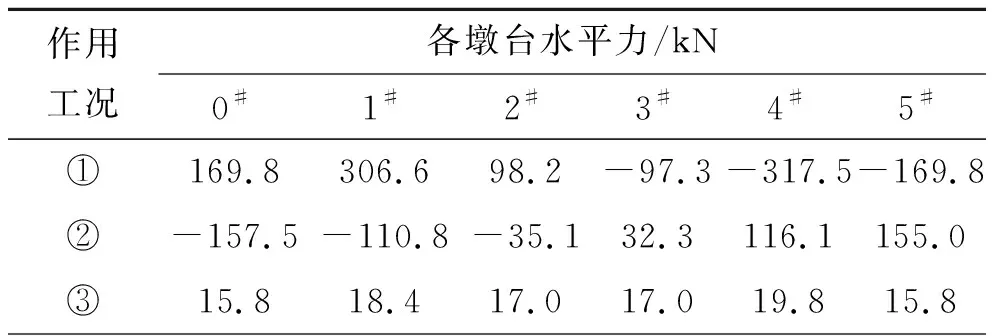
表2 墩台水平力计算结果

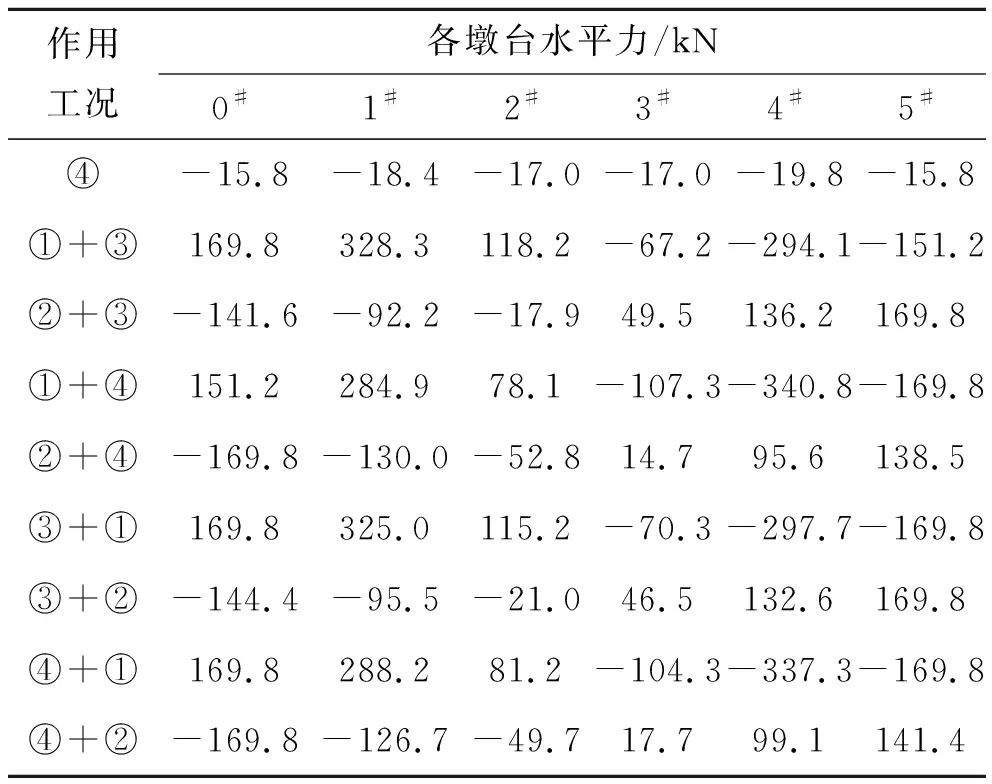
续表2

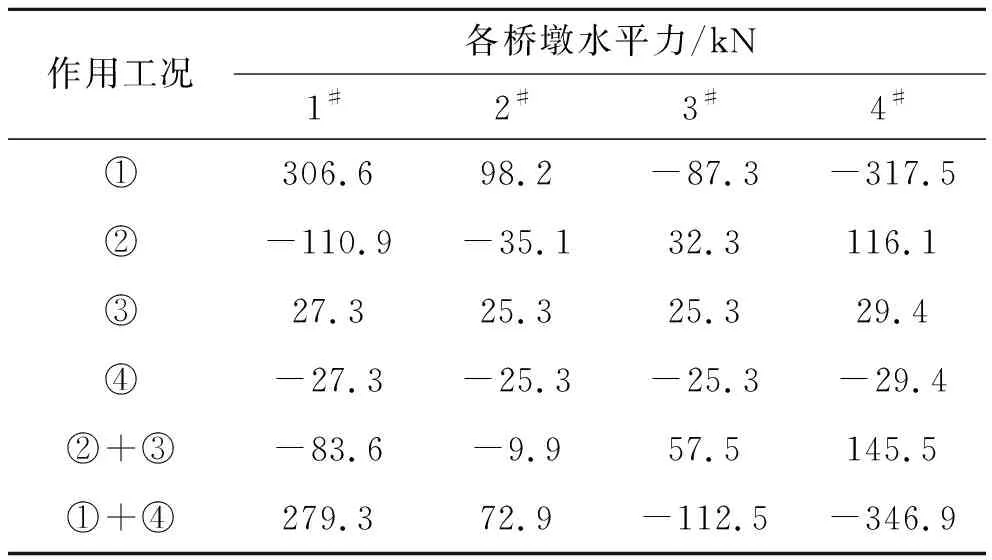
表3 文献[8]桥墩水平力计算结果

表中水平力方向规定为：正值表示水平力由0#台往5#台方向，负值表示水平力由5#台往0#台方向。

表中作用工况：①表示降温作用；②表示升温作用；③表示正向制动力；④表示负向制动力。

比较表2、3可以看出：① 工况①作用下，该文计算方法与常规计算方法得到的桥墩水平力结果相同。常规墩台水平力计算方法不考虑活动支座影响，纵向水平力在不设置活动支座的桥墩间分配，本质上是假定活动支座分配水平力默认为摩阻力的简化计算方法，不能准确给出各工况下，桥梁墩台的水平力计算结果；② 由表2可知：一般情况下，0#桥台与5#桥台的水平力，并不是同时达到摩阻力。该文给出的水平力分配分析方法，充分考虑活动支座的非线性影响和作用加载顺序，能够充分考虑活动支座水平力与摩阻力之间的关系，能够给出不同作用下各墩台的精确水平力结果，较常规方法而言，计算结果更趋合理。

6 结论

(1) 桥梁墩台顺桥向水平力计算，许多学者进行了大量的分析研究，提出了较多的计算方法，但总体而言，未考虑不同作用工况下，活动支座的非线性影响，通常将非线性问题简化成线性问题进行处理。

(2) 该文通过考虑活动支座的非线性影响和不同作用的加载顺序，提出墩台顺桥向水平力分配计算的非线性分析方法，计算结果表明:该方法能够充分考虑活动支座水平力与摩阻力之间的关系，给出不同作用下各墩台的精确水平力结果，计算结果更趋合理。