波浪力作用下环岛桥梁受力特性研究

李东洋， 郭馨艳， 高康平， 郭继业

(1.珠海市规划设计研究院， 广东 珠海 519000； 2.华南理工大学 土木与交通学院)

珠海市是台风多遇滨海城市，台风过境时常引起狂风巨浪，沿海桥梁直接遭受波浪威胁。尤其是在高潮水位的情况下桥梁有可能部分或全部淹没于水体中，此时桥梁上部结构会承受巨大的托浮力，梁体和下部墩柱会受到剧烈的波浪冲击力，这些都可能导致梁体发生错位乃至坍塌破坏。因此准确计算桥梁受到的波浪力，对沿海桥梁结构设计的可靠性和城市防灾减灾都具有重要的工程价值与现实意义。

关于波浪力对桥梁的作用，由于其力学机理比较复杂，因此大部分研究集中在试验研究和数值模拟分析。张家玮等通过缩尺比水槽模型试验研究了箱形截面桥梁受波浪力的作用；方庆贺在波浪水动力试验中采用包含主梁桥跨、临跨和桥墩的完整桥梁缩尺模型，测试了不同波浪要素下的波浪力；张宪堂等基于Fluent软件模拟了桥梁上部结构在数值波浪水槽中的受力状况，分析了波浪力大小、升阻力系数与波浪冲击高度的关系；Jin等采用CFD软件建立了桥梁上部结构在被波浪全淹没情况下的波浪力。

然而在实际沿海桥梁设计中，通过试验或复杂的流体力学数值模拟方法难以高效地为波浪设计荷载的计算提供依据。因此有学者在实际工程经验和物理模型分析的基础上提出波浪力的工程计算方法。Douglass等通过分析总结美国沿海桥梁在遭遇飓风落梁倒坍的原因，提出了竖直和水平波浪力的经验计算公式；McPerson改进了Douglass的经验公式，考虑了桥梁梁肋间俘获的空气对波浪力的加成；2008年美国公路运输管理协会AASHTO发布了估算桥梁所受波浪力的计算手册，综合考虑了波浪周期、波长、桥梁断面形式等因素对波浪力的影响；JTS 145-2015《港口与航道水文规范》给出了离岸式高桩码头面板底部波浪浮托力计算公式，桥梁受波浪的托浮力可以参考该公式进行计算，但该公式不能考虑桥梁断面形式对波浪力的影响。

该文以珠海市横琴新区某环岛路桥梁为例，针对桥梁上部梁体和下部墩柱遭受波浪力的受力状况，对比研究4种工程界应用较广的波浪力计算方法，分析各种方法的差异和优劣；并结合桥梁博士有限元计算软件对沿海环岛桥梁遭受波浪力的工况进行研究。

1 工程实例

广东省珠海市横琴新区某环岛路规划于横琴岛最南端，总长约3 km，桥梁长度约0.6 km，桥址选位直面海洋。桥梁方案采用预应力混凝土梁板式连续刚构桥，取其中一联(5+3×20+5) m进行受力计算和波浪力分析，桥梁立面和跨中标准横断面如图1、2所示。

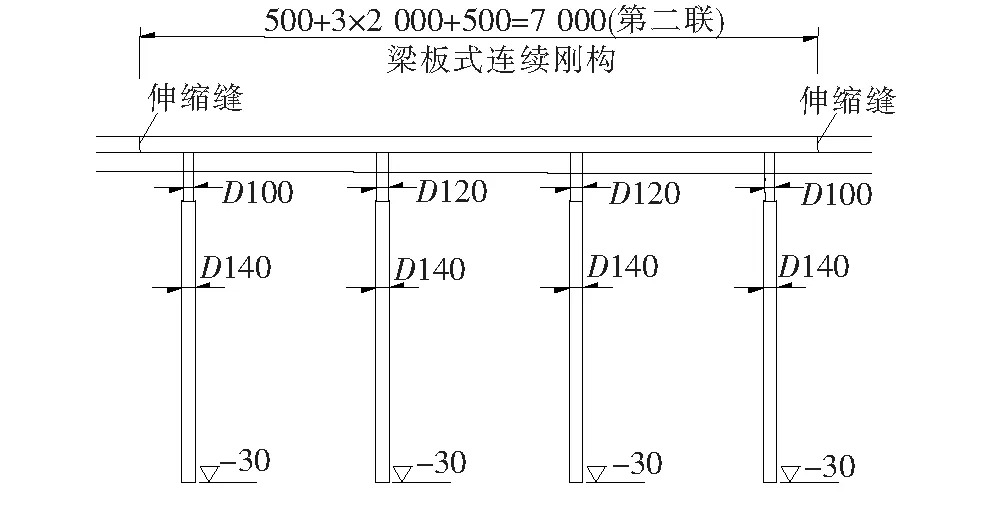
图1 桥梁立面图(除标高单位为m外，其余：cm)

图2 标准段桥型图(单位：cm)

桥梁采用的主要技术标准如下：① 标准断面宽：0.5 m(防撞防栏)+15.5 m(机动车道)+0.5 m(防撞防栏)=16.5 m；② 桥梁设计基准期：100年；③ 设计安全等级：一级；④ 环境类别：Ⅲ类；⑤ 汽车荷载：城-A级，人群荷载：3.5 kN/m2；⑥ 抗震要求：地震烈度按7度设防。

根据初步调查的水文资料，常水位为1.0 m，最高潮水位为3.74 m(P=1/100)，多年平均低潮水位为0.2 m(P=1/100)。桥址地区波浪要素为：100年一遇风速最大波浪高度H1%=1.413 m，周期为10.2 s，波长为78.516 m。桥面高程较低，在最高潮水位时，梁底与潮水位高差仅为0.16 m，因此桥梁设计时应考虑抗浮及波浪冲击的影响。为确保桥梁在波浪浮托力作用下结构安全，同时考虑到支座耐久性问题，不宜采用简支结构，须采用墩梁固结的形式，且应尽量减小跨径降低梁高。由于采用墩梁固结的方式，桥墩高度较低，下部基础采用单排桩，以增加桥梁纵向柔度。

2 波浪力计算原理

2.1 上部结构波浪力计算

(1) 中国规范

中国规范并没有明确提出桥梁上部结构受到波浪力的计算方法，但桥梁受到的竖直方向波浪力可以参考JTS 145-2015《港口与航道水文规范》给出的离岸式高桩码头面板底部受到的波浪浮托力和冲击力的计算方法进行计算。

桥面板纵向单位长度上受到的波浪最大托浮力计算式如下：

(1)

桥面板横向单位长度上受到的波浪最大冲击力计算式如下：

(2)

式中：γ为水的重度；x和x0为面板底部波浪作用宽度；H为入射波浪高度；K1为面板宽度影响系数；Δh为面板底部在净水面以上高度；η为波峰在静水面以上高度；C为波浪反射影响系数，对于面板下有纵横梁时取1.1，无纵横梁时取1；B为沿波浪传播方向的桥面板宽度；L为入射波波长；d为桥前水深。

但该规范没有给出离岸式高桩码头受到的水平波浪力计算公式。

(2) Douglass估算方法

国外对桥梁上部所受波浪力的研究开展较早，尤其是在2005年卡特里娜飓风给美国沿海桥梁带来巨大破坏后，许多学者将目光聚焦于桥梁在风暴海浪作用下的受力特点。为了方便工程师在设计中估算桥梁受到的波浪力，Douglass等提出了竖直方向和水平方向波浪力的经验计算公式，其力学模型如图3所示。

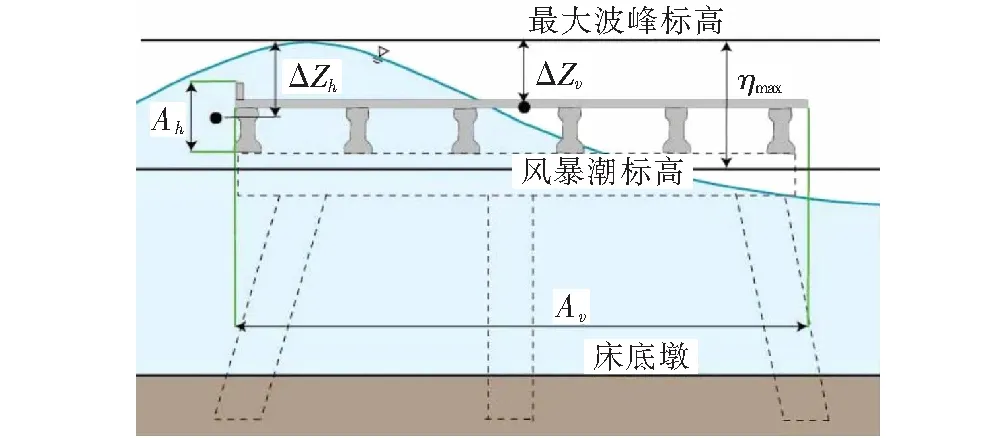
图3 Douglass估算方法示意图

考虑波浪冲击效应时，纵向单位长度的波浪力计算公式如下：

(3)

(4)

式(3)并没有考虑波浪淹没桥面时越浪对竖向波浪力的影响，因此使用该公式会高估桥梁被波浪淹没时受到的竖向波浪力。而且使用式(3)、(4)计算波浪波峰低于桥面情况的波浪力时，Δzv需调整为波峰与梁肋形心的高差，Δzh需调整为波峰与1/2梁高处(不包括栏杆)的高差。公式(3)、(4)也没用考虑桥梁梁肋间俘获的空气对波浪力计算的影响。

(3) McPerson改进方法

McPerson通过试验研究和理论分析改进了Douglass估算方法，考虑了波浪淹没桥梁时越浪对波浪力的影响，同时考虑了梁肋间俘获空气对波浪力的加成，其力学模型如图4所示。

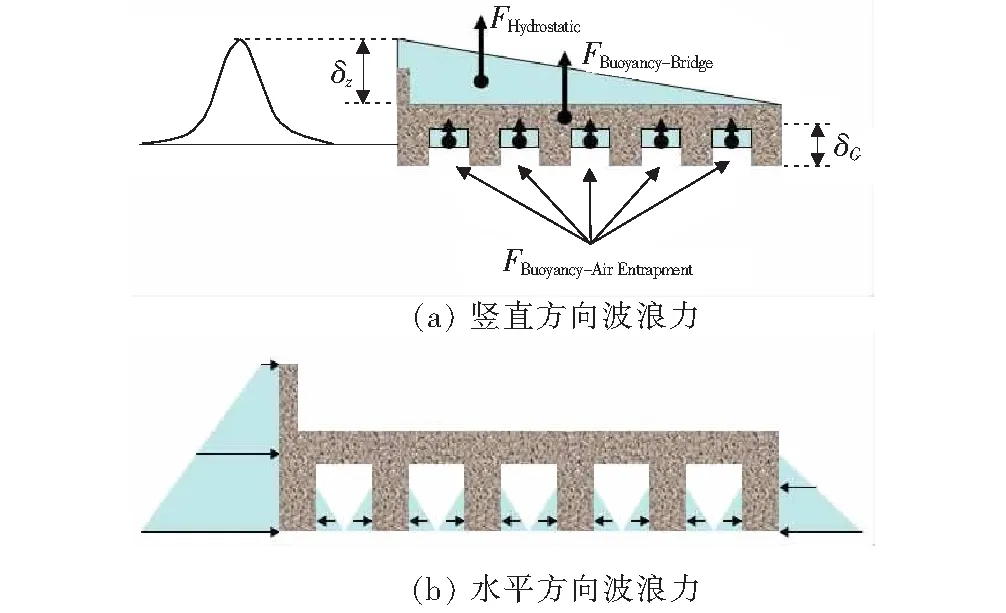
图4 McPerson改进方法示意图

纵向单位长度的竖直波浪力为：

FV-Total=FHydrostatic+FBridge+FAirEntrapment

(5)

FHydrostatic=γδzA-Fw

(6)

FBridge=γVolBridge

(7)

(8)

式中:FV-Total为总竖直波浪力；FHydrostatic为静波浪力；FBridge为桥体浸入水体产生的浮力；FAirEntrapment为梁肋间空气提高的竖向波浪力；δz为波峰到桥面的高差；δG为梁肋高度；Fw为波浪淹没桥面产生的反向力，该文将越浪部分近似为三角形或梯形，具体计算方法参考文献[9]；VolBridge为桥体浸入水体体积；AG为梁肋间空气体积，近似地计为1/2梁肋间空腔体积；n为梁肋数。

纵向单位长度的水平波浪力为：

FH-Total=FHydrostatic_Front-FHydrostatic_Back

(9)

当波浪淹没桥面时：

FHydrostatic_Front=0.5γ(ηmax-δG+ηmax-H1)H1

(10)

否则：

FHydrostatic_Front=0.5γ(ηmax-δs)H1

(11)

当潮水位低于梁底时：

FHydrostatic_Back=0

(12)

否则：

FHydrostatic_Back=0.5γ(H1-δG)2

(13)

式中：H1为梁高；δs为梁底到潮水位高差；ηmax为最大波高到潮水位高差。

(4) AAHSTO美国规范

2008年美国国家高速公路署(AAHSTO)发布了沿海桥梁波浪力计算规范。规范给出3种荷载组合的竖直、水平波浪力和弯矩的计算公式：组合1为最大竖向波浪力时对应水平力和弯矩；组合2为最大水平波浪力时对应竖直力和弯矩；组合3为计算梁体悬臂端受到的局部荷载，该文主要考虑前两种组合。图5为AAHSTO美国规范计算方法示意图。

图5 AAHSTO美国规范计算方法示意图

组合1波浪力计算公式：

(14)

(15)

(16)

式中:FV-max为竖直最大波浪力；Fs为竖向波浪冲击力；FH-AV为此时对应的水平波浪力;TAF为空气俘获系数。式中的各类参数意义详见文献[9]。

组合2波浪力计算公式：

FH-max=

(17)

(18)

FV-AH=

(19)

式中：FH-max为水平最大波浪力；Fs为竖向波浪冲击力；FV-AH为此时对应的竖直波浪力。

AAHSTO美国规范不仅考虑了桥址附近波浪的波高、周期和波长等波浪要素影响，还考虑了桥型(带肋梁和箱形梁)对波浪力的影响，是几种计算方法中最全面的一种计算方法。但该方法参数较大，在工程应用中也较为复杂。

(5) 计算结果分析

依据初步调查的水文资料和波浪要素，分别按照以上介绍的4种波浪力计算方法，算得该实例桥梁受到的波浪力，计算结果列于表1，其中竖向力是波浪竖直静力与冲击力之和。从工程偏于安全的角度考虑，该文取各计算方法获得的最大值作为波浪力设计值：依据JTS 145-2015《港口与航道水文规范》得到的竖向力最大，为160.52 kN/m，以其作为竖向波浪力设计值；McPerson改进方法得到的水平力最大，为12.27 kN/m，以其作为水平波浪力设计值。

表1 波浪力计算结果

2.2 下部墩柱波浪力计算

对于下部墩柱波浪力的计算，各国规范均基于Morison方程，只是在选择波浪理论和水动力系数上存在差异。JTS 145-2015《港口与航道水文规范》对于下部墩柱波浪力计算较全面，不仅有小尺度和大尺度桩的波浪力计算方法，还考虑了群桩的情况，因此该文对下部墩柱波浪力计算基于JTS 145-2015《港口与航道水文规范》。

对于小尺度桩柱，作用于水底以上高度z处的水平波浪力由速度分力PD和惯性分力PI组成，速度分力最大值PDmax和惯性分力最大值PImax分别为：

(20)

(21)

最大水平波浪总力Pmax计算公式为：

当PDmax≤0.5PImax时，Pmax=PImax

(22)

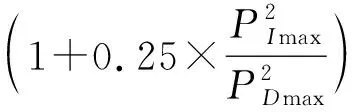
(23)

式中：CD为速度力系数，对圆形断面取1.2；CM为惯性力系数，对圆形断面取2；D为柱体直径；A为柱体断面面积；H为波高；K1和K2确定方法参见JTS 145-2015《港口与航道水文规范》。

求得该实例中波浪对桩柱的最大水平总力为13.82 kN。

3 考虑波浪力作用的受力分析

3.1 有限元模型的建立

将求得的波浪力导入桥梁博士4.0.2计算软件，对考虑波浪力作用的预应力梁板式刚构桥梁进行受力分析，按空间杆系对上部梁体和下部墩柱进行整体建模计算。共分为136个单元，主梁采用C50混凝土，按部分预应力混凝土A类构件进行验算；桥墩采用C40混凝土，按钢筋混凝土构件进行验算。按设计方案，主梁与桥墩的连接为墩梁固结，因此在有限元模型中桥墩和主梁采用刚性连接，中墩直径为1.2 m，边墩直径为1 m，桥墩高均为5 m。由于工程现场地质较好，岩面普遍较高，因此墩底边界条件设为固支。

桥梁自重由软件自动计算；二期荷载包括桥面铺装与护栏，按均布荷载加载到梁单元上；汽车荷载为城-A级；冲击系数μ=0.366；温度作用包括整体升温、降温取±25 ℃；基础不均匀沉降按5 mm考虑。在结构计算时需同时考虑波浪力存在与否的两种荷载组合：组合1为恒载+汽车活载+温度变化+沉降+收缩徐变；组合2为恒载+汽车活载+波浪力+温度变化+沉降+收缩徐变。

3.2 计算结果分析

3.2.1 波浪力对应力分布的影响

竖直波浪力是与恒载和汽车活载方向相反的力，因此考虑波浪力作用时预应力主梁的钢束设计需要在有无波浪力作用两种荷载组合下不断调整，直至钢束配置同时满足这两种荷载组合。图6为是否考虑波浪力两种情况时主梁运营阶段短期组合和标准组合正应力云图(正为压应力，负为拉应力)。部分预应力混凝土A类构件标准值组合压应力容许值为0.5×32.4=16.2 MPa，拉应力容许值为0.7×2.65=1.855 MPa；从图6可以看出：运营阶段应力满足规范要求。不考虑波浪力时，主梁结构只存在压应力；考虑波浪力时，由于竖直波浪力对梁体有整体上托的作用，主梁中墩处产生了拉应力0.53 MPa，但仍小于拉应力容许值1.855 MPa。

图6 主梁运营阶段短期组合和标准组合下正应力云图(单位：MPa)

3.2.2 桥墩高度的影响

该环岛桥梁为预应力混凝土连续刚构桥，桥墩较矮时，温度变化、不均匀沉降和预应力等因素使桥墩产生的次内力较大，同时波浪力也有可能对结构内力分布产生不利影响。按照设计方案桥墩高度为5 m，图7为施工阶段桥墩截面的压应力云图。由图7可以看出：当桥墩高度为5 m时，边墩压应力远大于中墩压应力；而且墩顶、底的压应力超过施工阶段压应力容许值0.8f′ck=21.44 MPa，说明桥墩5 m过矮导致结构内力分布不合理。

图7 施工阶段桥墩压应力(单位：MPa)

表2为桥墩高度为5、7.5、10 m时，考虑与不考虑波浪力作用时桥墩截面的最大压应力。由表2可以看出：在施工阶段，随着桥墩高度从5 m增至7.5 m，边墩和中墩的压应力分别减小了47.1%和53.7%；当桥墩高度增至10 m时，边墩最大压应力为21 MPa，小于施工阶段压应力容许值0.8f′ck=21.44 MPa，说明桥墩高度要达到10 m才满足规范要求。在运营阶段，桥墩高度为5～7 m时，考虑波浪力边墩压应力平均要比不考虑时大3.3%～5.1%，而且墩长越长，波浪力影响越大；波浪力对中墩压应力影响不明显。

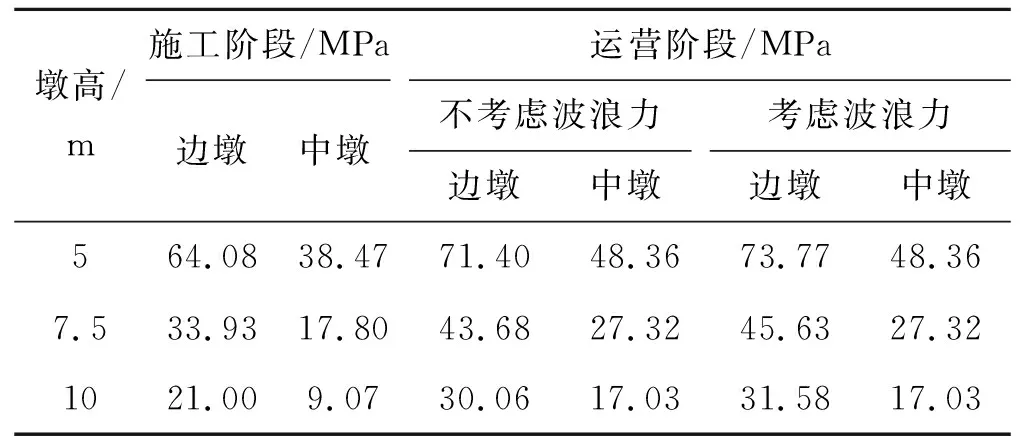
表2 不同墩高时桥墩截面最大压应力

3.2.3 墩柱连接方式的影响

由上节分析可知，桥墩高度需达到10 m才能满足规范验算的要求。但由于该环岛桥梁桥面高程已被限定，桥面到海床的平均高差约为5 m，若设计桥墩高度达到10 m，近5 m的桥墩需进入海床。当然桥址海床普遍较好，但因桥墩进入河床需要保持其柔度而产生的施工措施费用(如进入河床的桥墩外加钢护筒，桥墩与钢护筒间填充柔性材料)会大大增加桥梁造价。为此，可将边墩与主梁的连接模式由墩梁固结改为铰支连接，中墩则保持墩梁固结，重新计算看是否能释放边墩的次内力，降低桥墩高度。

图8为边墩铰支、中墩固结，边墩和中墩高均为6 m时的施工阶段桥墩截面压应力云图。由图8可以看出：此时边墩压应力大大减小，中墩压应力最大值为21.04 MPa，小于施工阶段压应力容许值0.8f′ck=21.44 MPa，满足验算要求。说明将边墩由墩梁固结改为铰支连接，能使桥墩高度减小40%。

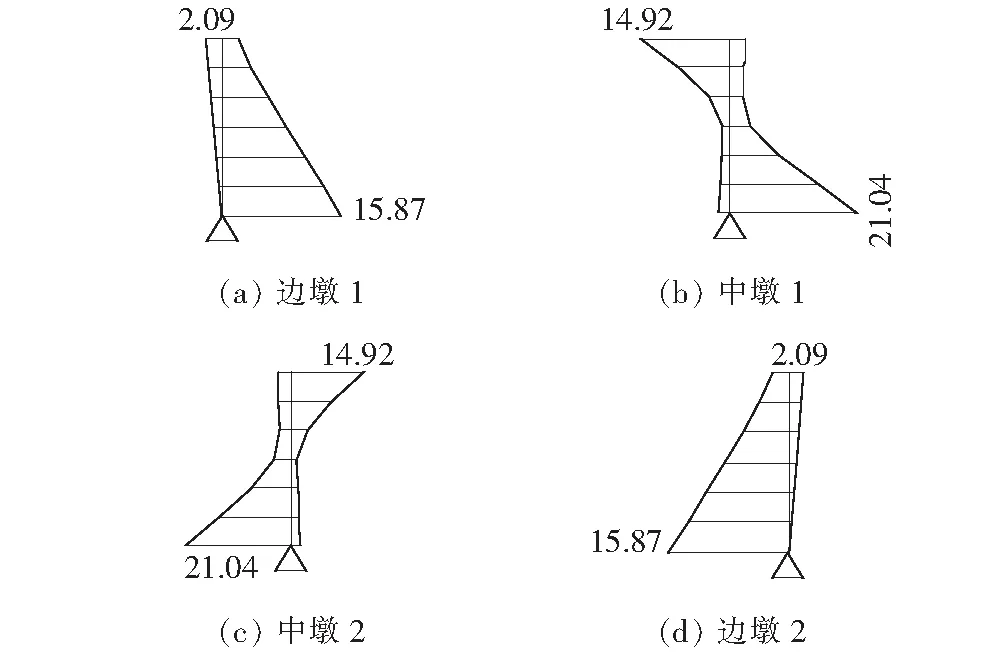
图8 边墩铰支中墩固结时施工阶段桥墩压应力(单位：MPa)

图9为考虑波浪力作用时，运营阶段边墩和中墩上下缘正应力云图。由图9可以看出：在波浪力作用时，桥墩截面均为压应力不存在拉应力，说明了在波浪力作用下边墩的铰支座不会脱空。

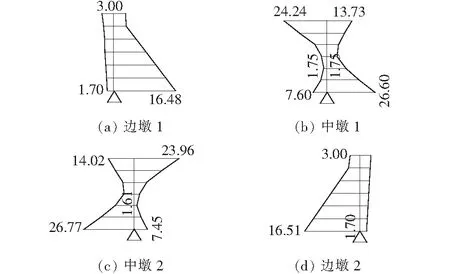
图9 考虑波浪力作用时桥墩上下缘应力云图(单位：MPa)

4 结论

以横琴新区某预应力混凝土连续刚构桥梁为例，针对桥梁上部梁体和下部墩柱所受波浪力，比选研究了波浪力计算方法；结合桥梁博士有限元计算软件对桥梁在波浪力作用下进行受力分析，得出如下结论：

(1) 对于桥梁上部梁体受到的波浪力，有4种工程界应用较广的计算方法，其中JTS 145-2015《港口与航道水文规范》计算得到的竖向波浪力最大，为160.52 kN/m；McPerson改进方法计算得到的水平力波浪力最大，为12.27 kN/m。从工程偏于安全考虑，该文取这两个值作为波浪力设计值。

(2) 对于下部墩柱波浪力，JTS 145-2015《港口与航道水文规范》计算较全面，计算得到波浪力为13.82 kN/m。

(3) 通过有限元计算可知，主梁运营阶段应力满足规范要求。考虑波浪力时，由于竖直波浪力对梁体整体有上托的作用，主梁中墩处拉应力增加。

(4) 采用墩梁固结的方式时，因桥墩较矮，温度变化、不均匀沉降和预应力等因素使桥墩产生的次内力较大，同时波浪力对结构内力分布产生不利影响。而且桥墩高度要达到10 m才满足规范要求；墩长越长，波浪力影响越大。

(5) 将边墩与主梁的连接模式由固结改为铰支，能有效减小桥墩次内力，从而降低桥墩高度。