基于索力损伤向量的斜拉桥结构损伤识别

秦伟亮， 孙宗光， 曲翔雨， 司琦， 伦卓

(大连海事大学 交通运输工程学院， 辽宁 大连 116023)

大跨桥梁结构的使用期长达几十年、甚至上百年，环境侵蚀、材料老化、荷载的长期效应、疲劳效应与突变效应等灾害因素的耦合作用将不可避免地导致结构和系统的损伤积累和抗力衰减, 从而抵抗自然灾害、甚至正常环境作用的能力下降，极端情况下引发灾难性的突发事故。仅凭以往的间歇性的检测和评价，难以满足确保结构安全运营的要求。因此，近20年来结构长期健康监测系统，得以迅速发展。如何利用结构健康监测系统采集到的响应信息反演出桥梁结构的工作状态，这是实现大跨桥梁结构损伤识别与状态评估的关键问题。为此，众多学者对其进行了大量的研究。斜拉索作为斜拉桥主要的承力构件，连接着主梁和主塔并且分布广泛，本身含有桥面和主塔结构的空间位置信息，而对于斜拉索和索力的相关研究大多停留在斜拉索发生损伤的识别上。文献[6]首次提出了索力损伤识别指标，并探讨了对不同损伤工况的敏感性和稳定性，显示了较好的基于该指标进行斜拉桥损伤识别的可行性；文献[10、11]采用了索力损伤指标，但损伤识别仅是对主梁的损伤识别。该文以青岛海湾大桥沧口斜拉桥为分析对象，面向实际监测索力，提出了基于统计特性而构建的索力损伤向量。基于经修正后的有限元模型，研究了基于该索力损伤向量进行单损伤和组合损伤识别分析方法。该方法可通过对全部或部分斜拉索的索力监测，实现对斜拉桥结构的一部分损伤进行识别和健康状态评价。

1 模型修正与监测索力模拟

1.1 模型修正

沧口桥实景图如图1所示，1/2跨立面布置如图2所示。首先，运用Ansys有限元分析软件创建初始有限元模型；其中，主梁采用Beam4单元，主塔和墩采用Beam188单元，斜拉索采用Link10单元。然后，以荷载试验和部分监测结果为目标，采用响应面法进行静、动力模型修正。修正后模型计算的前几阶主要模态频率和静态索力值与实测值的比较如表1、2所示。

图1 沧口桥实景图

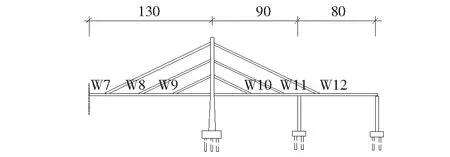
图2 沧口桥1/2跨立面图及索的编号(单位：m)

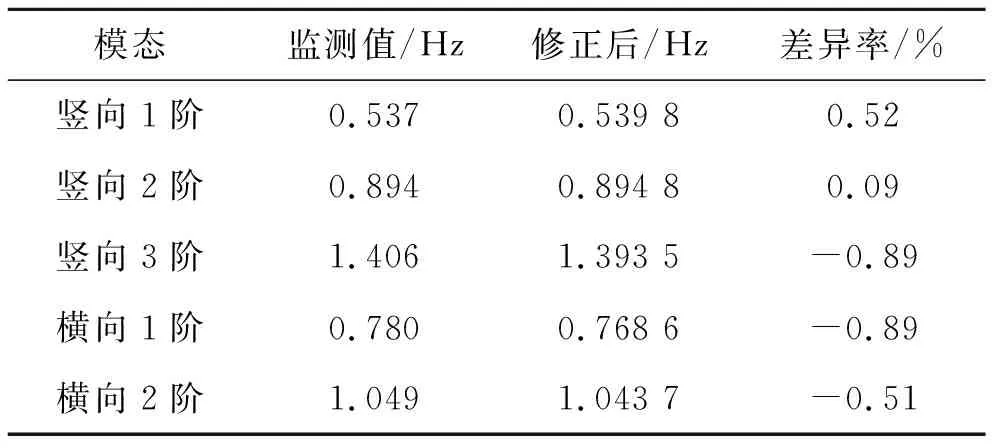
表1 修正后模型与实测振型频率对比

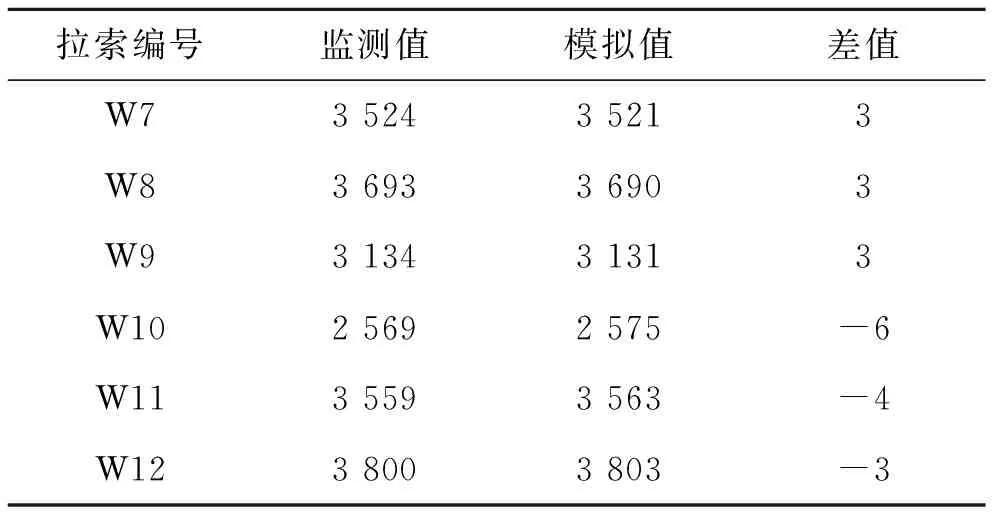
表2 静态索力实测值与模拟值对比 kN

1.2 监测索力模拟

采用基于监测索力构建的指标进行损伤识别，宜选用相对稳定可靠的索力监测数据。正常运营环境下索力主要受温度、车辆和其他随机干扰因素的影响。

为此，首先选用夜间时段数据以尽量消除日照温度的影响。再通过数据分解分离高频随机干扰部分和车辆荷载导致的索力突变。然后在年周期内选取每天同一时段的数据为样本，分析建立年温度与索力的统计关系。分析表明：年温度与索力之间呈现显著的线性相关性。基于监测年温度数据样本及其分布特性进行温度加载，由修正的有限元模型计算得到模拟索力。年温度与实测索力和模拟索力的关系对比如图3所示。实测索力和模拟索力二者在分布规律及与温度的相关关系方面吻合较好。表明修正的有限元模型能够较好地反映索力与环境温度的关系。

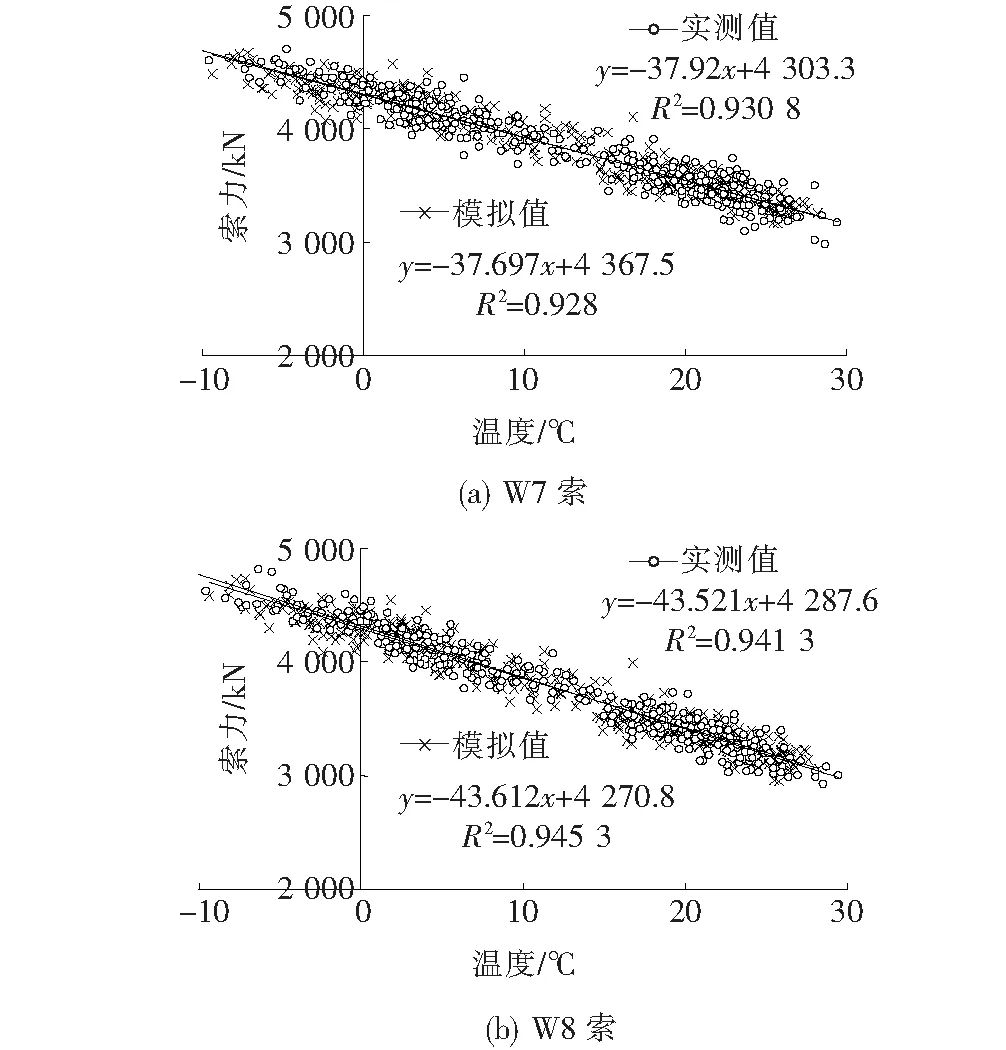
图3 实测与模拟索力-环境温度关系比较

由于全年索力F与温度T之间具有较高的线性相关关系，可通过式(1)消除温度对索力的影响，把得到的新索力Fs称为标准索力。

Fs=F-k(T-Tb)

(1)

式中：Fs为标准索力；F为索力；k为索力与环境温度关系的斜率；T为环境温度；Tb为基准温度(此处取15 ℃)。

标准正态分布检验结果表明：标准索力Fs符合正态分布。2012年W7索全年实测索力和模拟索力的标准值分别如图4、5所示。以下的损伤识别分析将基于标准索力。

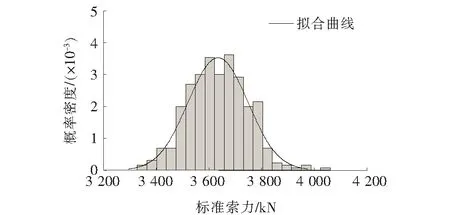
图4 W7索的标准索力实测值

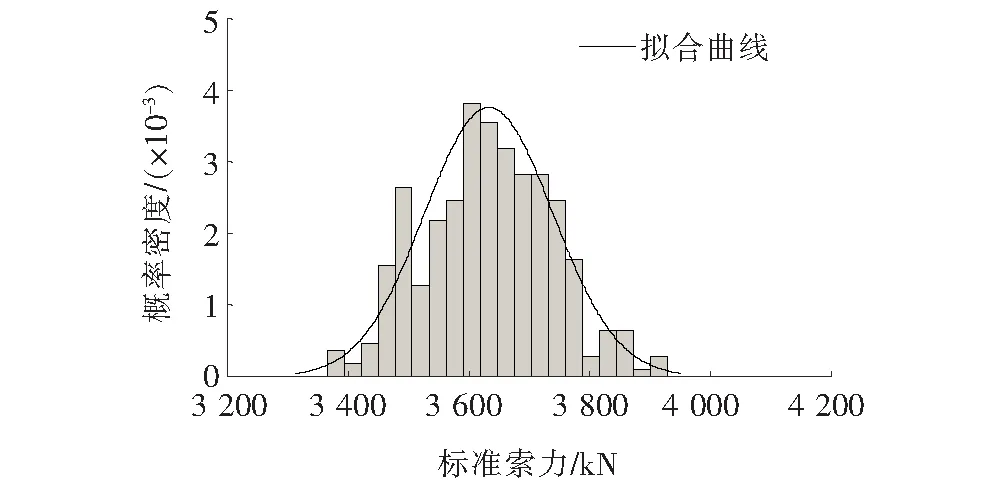
图5 W7索的标准索力模拟值

2 损伤敏感性分析

通常情况下拉索索力对该区域的损伤更敏感，因此根据结构对称性将斜拉桥划分为4个区域，针对各区域的损伤工况采用该区域索力进行损伤分析和识别。这里以一个区域为例来阐述损伤分析和识别方法。首先基于斜拉桥易损性分析的相关文献以及根据该桥静载情况下的易损性分析，在该区域选取8种损伤工况。其中工况1、2为索损伤，3、4为主塔损伤，5、6、7为主梁损伤，8为整体老化。前7种工况的损伤位置如图6所示。

图6 第1～7种损伤工况的损伤位置(单位：m)

模拟损伤方法很多，该文采用降低构件弹性模量的方法模拟损伤。为得到标准索力分布特性与损伤程度之间的关系以及索力均值随损伤程度的变化趋势和趋势方程，分别模拟了各损伤工况0～70%的损伤程度。计算结果表明：索力均值对这几种损伤工况都较敏感，而索力标准差敏感性较差。限于篇幅，这里仅列出工况2的W10索标准索力分布特性变化情况(如图7所示)，以及相应的索力均值改变量与损伤程度的趋势(如图8所示)。

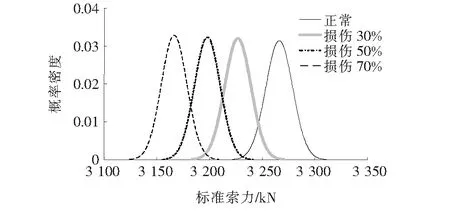
图7 W10索标准索力分布特性(工况2)

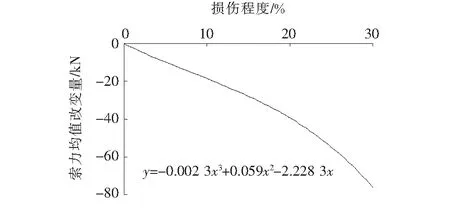
图8 W10索力均值改变量与损伤程度趋势线(工况2)

由图8可见索力均值随损伤程度呈显著变化，而标准差最大改变量仅为为-0.559 4 kN；故选用索力均值作为损伤识别指标。

由损伤敏感性分析可得：斜拉索不仅平衡主梁自重更使主梁产生拱度，而主梁具有一定的抗弯刚度；当主梁发生损伤，索力必然发生变化。主塔两侧索力也不完全平衡，从而在桥塔内产生可观的弯矩，故主塔损伤也必然引起索力变化。对于斜拉索，当拉索发生损伤必然引起索力重分布。随着时间推移，斜拉桥结构构件会发生老化致使刚度降低(包括梁、塔、索)，索力必然发生明显降低。

3 损伤识别

采用标准索力个别值抽样例行监测评价，该方法较为简单，但有很大的局限性。如果结构发生显著改变，必然会导致索力分布特性发生显著改变，但是索力个别值仍然可能处于正常值域，这时，上述评价方法就会失效。因此，基于分布特性的索力状态评价才是更为可靠和科学的方法。但根据一根索索力分布特性的改变来识别损伤是很难做到的，因此，采用一组索索力分布特性的改变模式来识别损伤才有实现的可能。

以6根索的标准索力均值的改变量作为一组列向量α={w7w8w9w10w11w12}T。根据向量与向量之间的相关性来研究不同损伤工况及相同损伤工况不同损伤程度的损伤向量之间的关系。

3.1 单损伤识别

通过损伤敏感性分析，可以得到前文所述8种损伤工况的损伤向量。“模态置信准则”(MAC-Modal Assurance Criterion) 通常可用于检验两个向量之间的相关性：

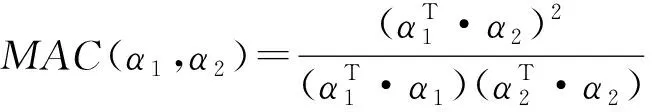
(2)

MAC值总是在[0,1]区间内变化，越靠近1表示α1、α2的相关性越好。但要谨慎区分“虚假”的MAC值。对同一损伤工况不同损伤程度之间的损伤向量进行MAC检验，其结果如表3所示。而对同一损伤程度下的不同损伤工况之间损伤向量的MAC检验结果如表4所示。

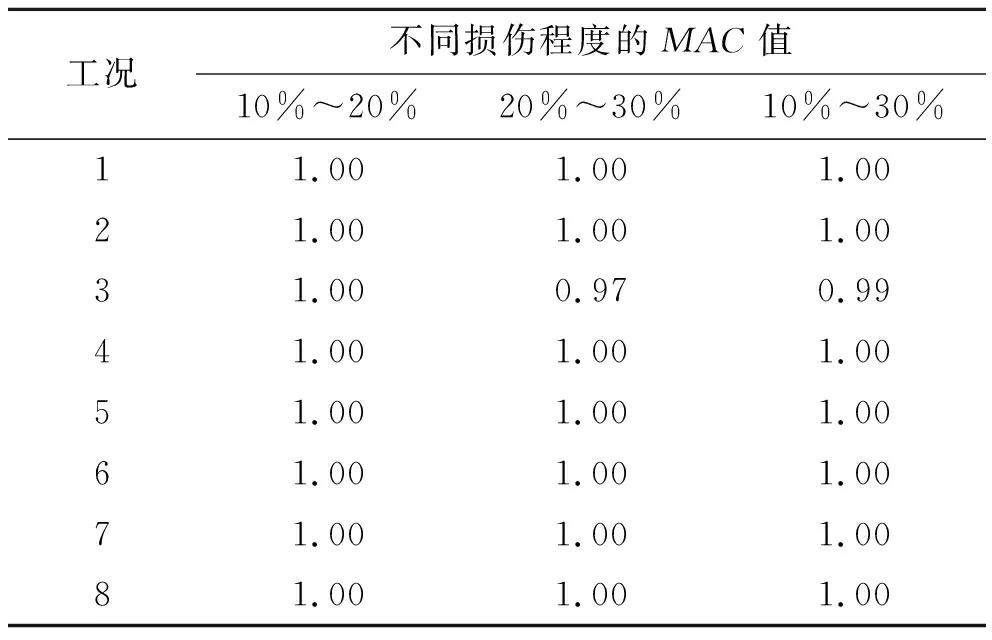
表3 同一损伤工况不同损伤程度损伤向量之间的MAC值

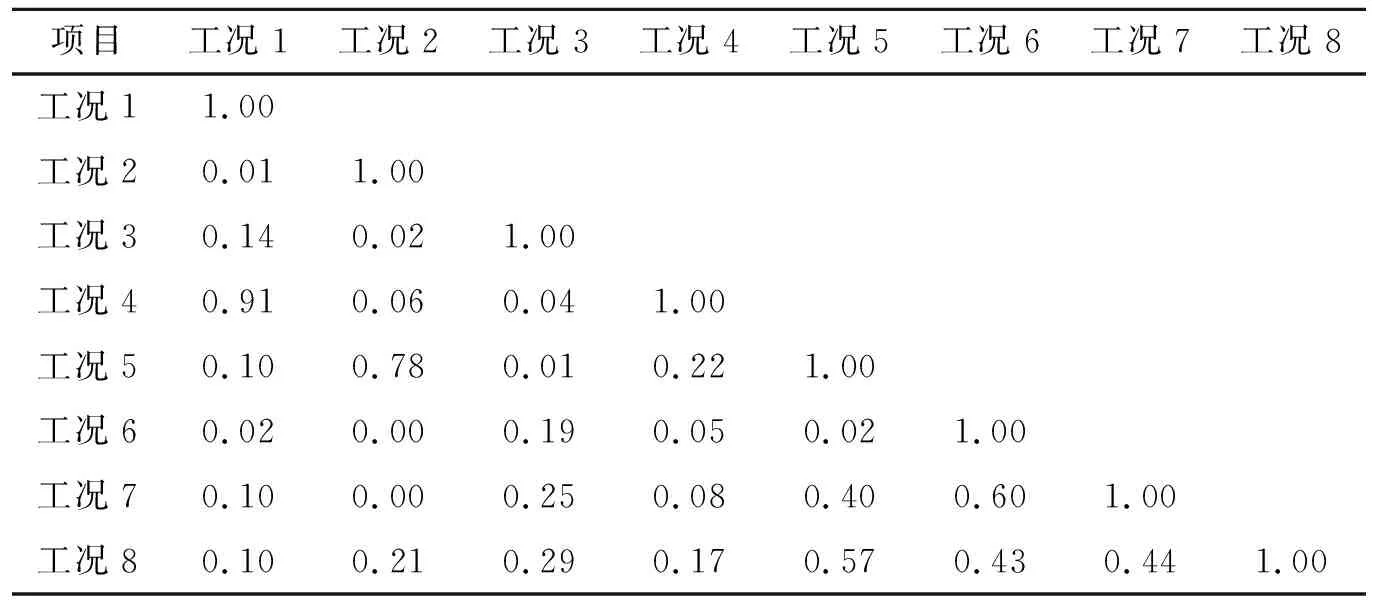
表4 不同损伤工况相同损伤程度损伤向量之间的MAC值

表3、4表明：① 只要是同一损伤工况，不同损伤程度的损伤向量之间都具有高度相关性；② 不同损伤工况之间，即使损伤程度相同，其损伤向量之间相关性也较差。以上两点显示了通过由索力构造的损伤向量识别损伤的可行性。对于表4中两工况的MAC值较大“虚假”的情况，可暂把此损伤工况作为一种损伤可能。在计算损伤程度的时候，可将此“虚假”损伤排除。

基于以上损伤向量的相关性分析可知，有的损伤工况易发生混淆。为此，下面模拟工况1损伤程度5%的情况作为“未知的损伤”来阐述该文的损伤识别方法。

首先，模拟“工况1损伤程度5%”，得到损伤向量α={-1.3 -4.4 -13.5 19.9 7.5 2.4}。然后，将上述损伤向量与全部8种损伤工况的某同一损伤程度(不妨选取30%)的损伤向量求MAC值，计算结果如表5所示。

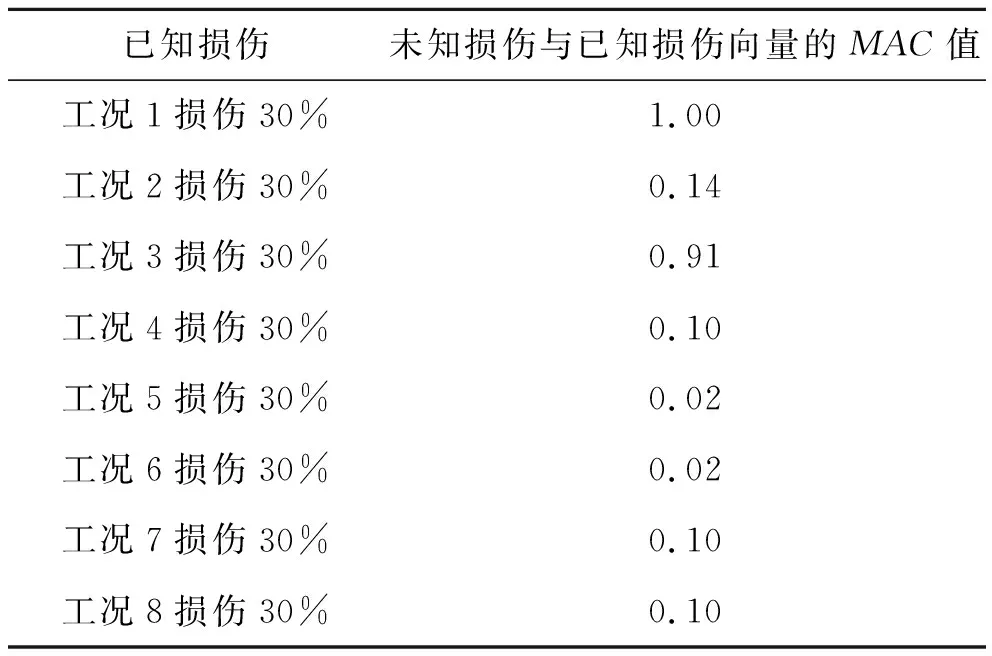
表5 未知损伤向量与已知损伤向量的MAC值

表5表明：未知损伤应该是工况1或工况3当中的某一种工况。下面通过识别损伤程度来排除“虚假”损伤。由损伤敏感性分析可以得出各单损伤工况的均值改变量与损伤程度趋势线，并求出如图8所示的趋势方程。将未知损伤工况的均值改变量分别代入与之相应的工况1与工况3的趋势方程中，求解损伤程度。如果求解的损伤程度为0～100%且数值接近，就可以确定损伤工况及损伤程度。计算结果见表6。

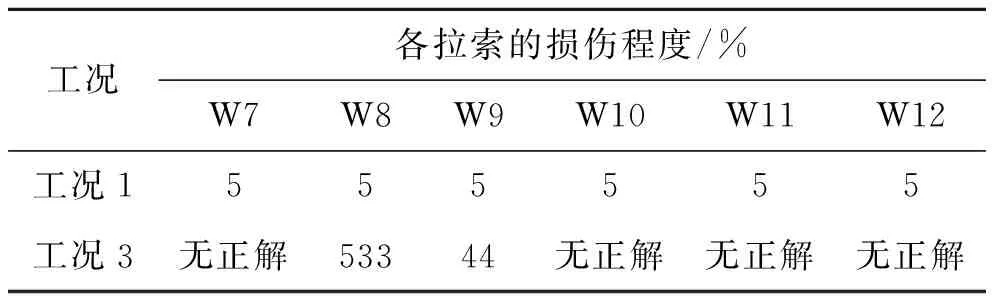
表6 求解的损伤程度

由表6，可以将工况3排除，确定未知损伤为工况1，损伤程度为5%。用该方法进行损伤识别，部分损伤识别结果如表7所示。

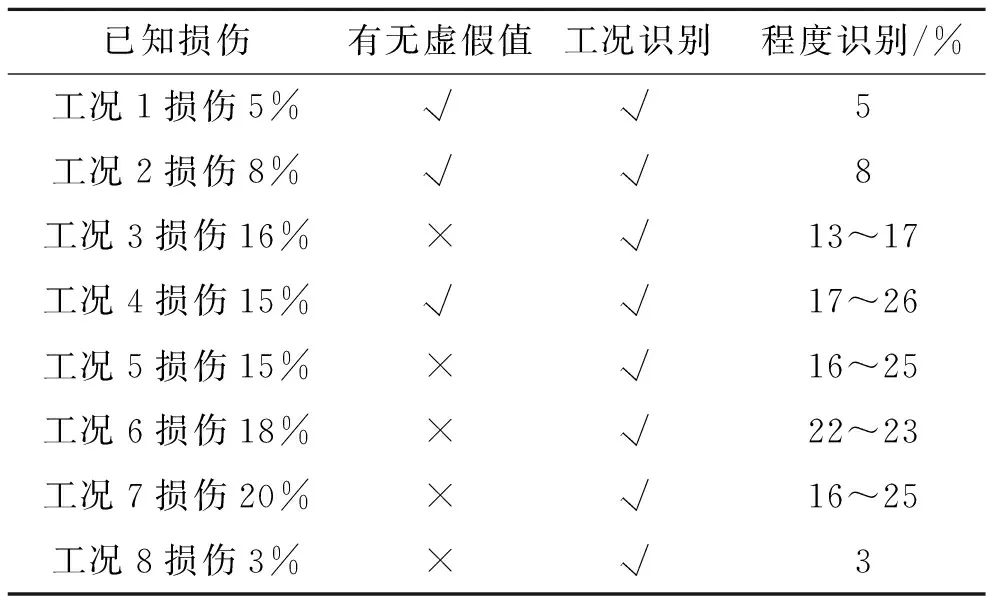
表7 损伤识别结果

3.2 组合损伤识别

组合损伤是指两种损伤工况的组合损伤。通过数值模拟得出，组合损伤向量可近似看成这两种单损伤向量的线性叠加。假设待识别的未知损伤工况是上述8种损伤工况中某两种单损伤工况的组合。

首先，选取每种单损伤工况任意两种已模拟的损伤程度的损伤向量(该文选取10%、30%)，并将8种单损伤工况两两组合(共28组)，每组一共4个损伤向量。

其次，选取第i组的4个单损伤的损伤向量[αi1αi2αi3αi4]T，i=1,2,3，…，28。假设存在正交向量βi={xi1xi2xi3xi4xi5xi6}T,使得:

[αi1αi2αi3αi4]T·βi=0

(3)

求正交向量βi(由6个未知数4个方程可知该方程有两个线性无关的正交向量βi1、βi2)。以同样的方式求解出所有组的正交向量。

最后，把未知损伤的损伤向量α的转置αT与这28组损伤工况的正交向量βi1、βi2相乘，当得到的数值ai1、ai2(i=1,2,3,…,28)越接近于0，则未知损伤工况为该损伤工况的概率越大；当得到的值ai1、ai2大于1时，则未知损伤工况为该损伤工况的概率基本为0。计算方程式如下：

(4)

其中：αT为未知损伤的损伤向量；βi1、βi2为第i组的正交向量。限于篇幅，该文仅提供一例加以佐证。

模拟“工况1损伤5%+工况2损伤7%”的组合损伤作为待识别的组合损伤工况，得到损伤向量。将α={-151.4 18.1 -8.1 21.6 -5.1 -20.7}代入式(4)得到的结果取绝对值，由于数值偏差较大，该文只给出[0,1]区间的结果展示，如图9所示(图中解1表示ai1，解2表示ai2)。

由图9得出：未知损伤为工况1+工况2组合损伤的概率高达90%以上，其他组合损伤的概率基本为0，但不能排除未知损伤为工况1或工况2的单损伤的可能性。为识别损伤，采用3.1节中单损伤识别的方法进行识别，结果为与工况1的MAC值为0，与工况2的MAC值为0.95。

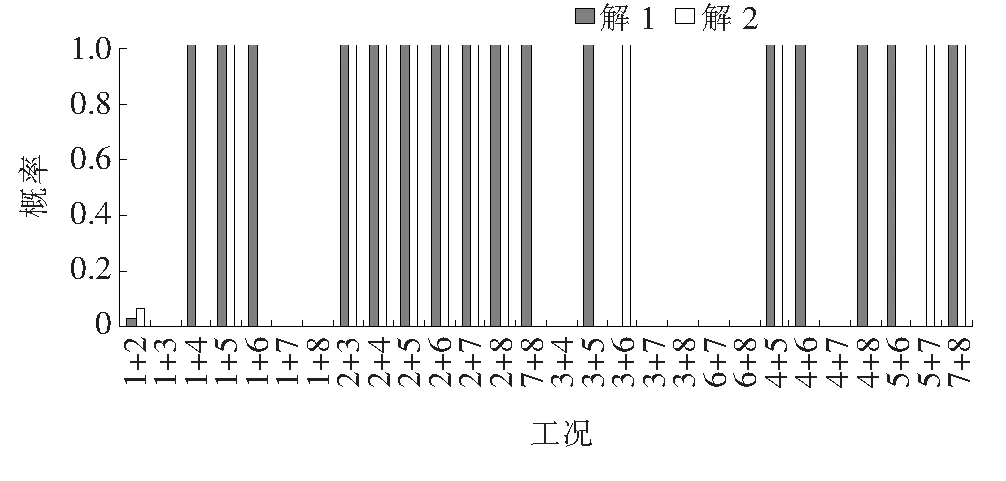
图9 未知损伤向量与解向量的乘积

由此可得：未知损伤与工况2的单损伤相关性较高，与工况1的相关性很差，故把工况1的单损伤情况排除。用3.1节中求单损伤程度的方法求解损伤程度，求解结果见表8。

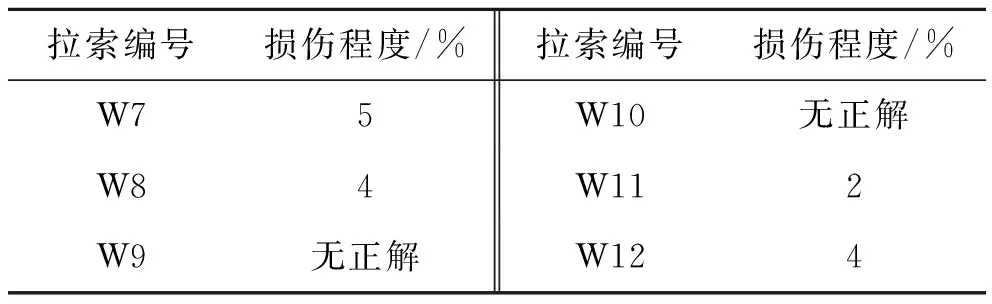
表8 工况2求解的损伤程度

通过表8，可以将工况2的单损伤可能性排除，并确定损伤工况为工况1+工况2的组合损伤工况。用该方法进行损伤识别，部分组合损伤识别结果见表9。

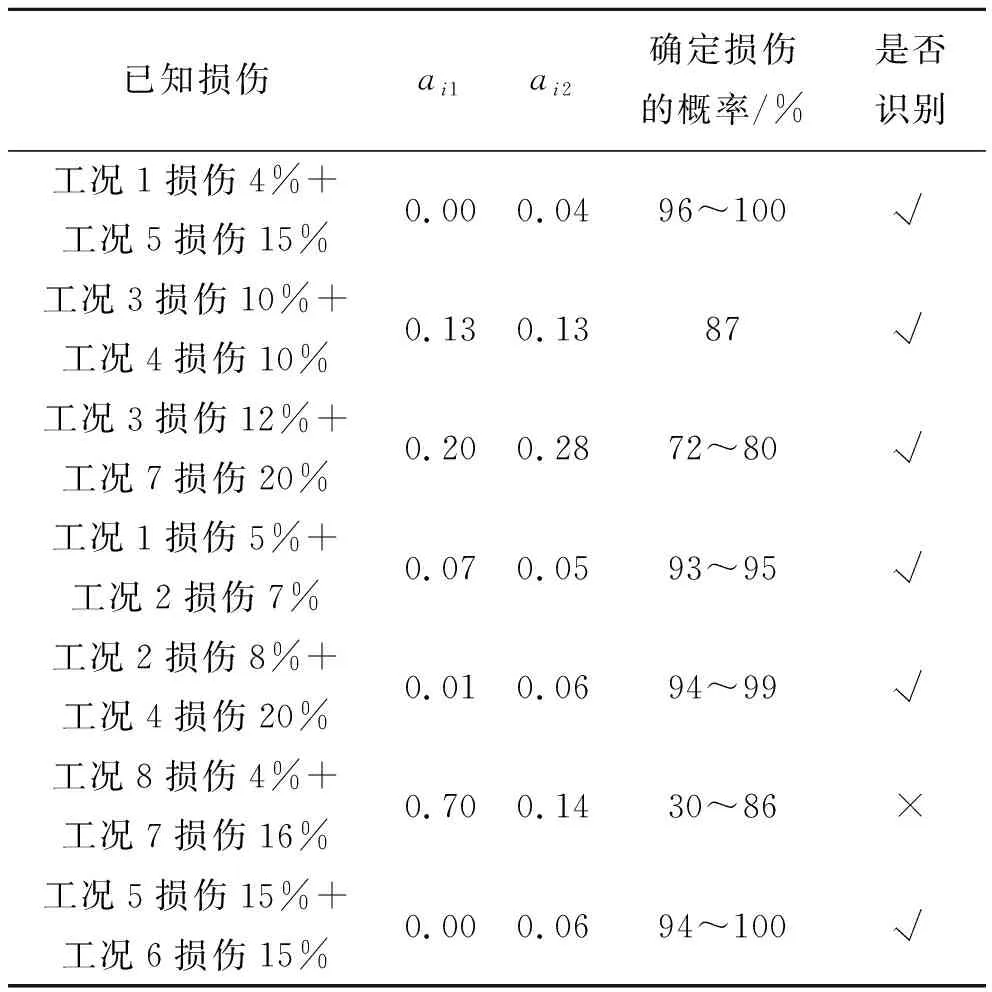
表9 组合损伤识别结果

3.3 损伤个数识别

众所周知，在实际工程中损伤个数是无法预知的(此处损伤个数为1个或2个)，损伤个数未知就无法判断用单损伤识别还是组合损伤识别。然而，如果用组合损伤识别的方法判断单损伤，那么包含此单损伤的所有组的正交向量βi1、βi2与未知单损伤的损伤向量转置αT的乘积ai1、ai2都应该接近于0。

下面以3.1节中的单损伤例子加以证明，“工况1发生5%”的损伤，得到标准索力均值改变量向量α={-1.3 -4.4 -13.5 19.9 7.5 2.4}，用组合损伤识别的方法进行识别得到结果，如图10所示。

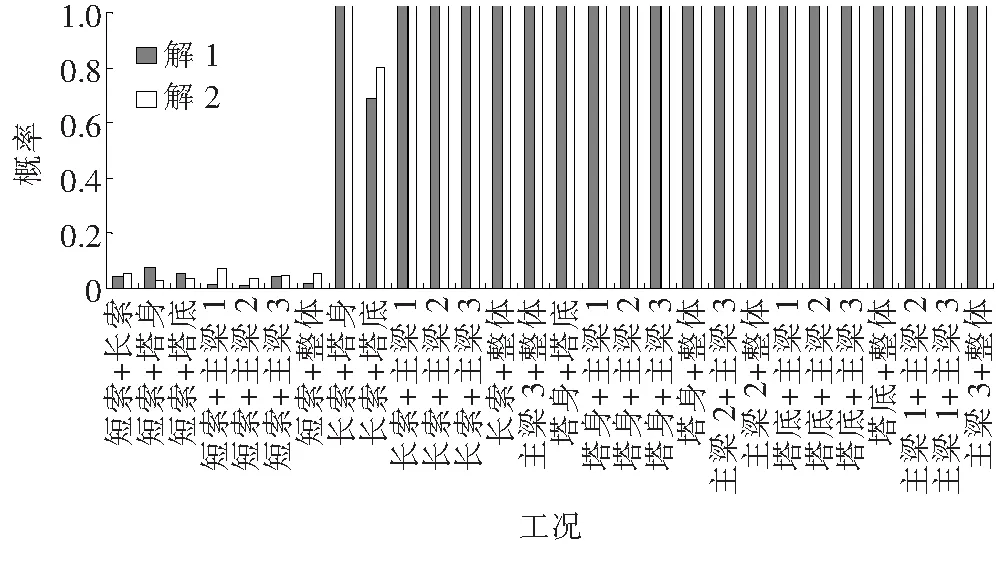
图10 未知损伤向量与正交向量的乘积

由图10可知：包含单损伤工况1的7种组合损伤的正交向量βi1、βi2与未知损伤向量转置αT的乘积ai1、ai2都趋近于0，这与预期一致。由此得出一套未知损伤识别的方法：在得到未知损伤向量α之后，先用组合损伤识别的方法进行验证，如果只有一组正交向量βi1、βi2与未知损伤向量转置αT的乘积ai1、ai2都趋近于0，那么就可以确定损伤工况为该组合损伤；如果有包含某一单损伤工况的所有组的正交向量βi1、βi2与未知损伤向量转置αT乘积ai1、ai2都趋近于0，那么就可以确定损伤工况为此单损伤，并可用单损伤识别的方法加以确定，并计算出损伤程度。

4 结论

以索力构造损伤向量是基于索力相对稳定，易于监测、便于应用的特点，并且斜拉索本身包含了桥面和主塔结构的空间位置信息，因此以索力作为损伤识别指标具有可行性。通过对索力损伤向量的研究，得出以下结论：

(1) 只要是同一损伤工况，不同损伤程度的损伤向量之间都具有高度相关性；不同损伤工况之间，即使损伤程度相同，其损伤向量之间相关性也较差。由此可显示基于索力构建损伤向量的损伤识别具有显著可行性。

(2) 该文方法不但可以识别单损伤情况，结合损伤程度的分析，也可以较好地识别多损伤情况；并且可以有效地区分损伤个数。