基于有限元分析提升家具结构强度的应用研究

黄鹏飞，李芳菲，张 磊

(上海市质量监督检验技术研究院, 国家家具质量检验检测中心， 国家建筑材料及装饰装修材料质量检验检测中心，上海 201114)

1 家具质量现状及重组竹简介

目前，我国的家具设计和制造倾向于注重家具的外形和材质，外形美观、使用舒适的家具越来越多，家具的人体工程学符合度有了进一步的提升，但家具结构仍处于直觉设计和经验设计阶段[1]。从以往送检的木家具产品中可以看出，家具结构设计常常呈现两极分化的现象：一种现象是不合理的结构和用材导致产品在力学性能试验过程中或是发生破裂、变形或是倾翻，达不到标准要求，此类产品多为板式家具[2]；另一种现象则是家具用料足、做工精细，在全项力学性能试验后，家具仍旧具有较好的完整性和结构强度，但家具过为笨重，给使用和搬运带来不便，此类产品多为实木家具，在我国木材短缺的现状下，造成了木材的浪费。

家具产品检测通常只能得到产品合格与否的结果，没有过程数据，无法为结构设计提供更多的指导意义，而有限元分析能较好地弥补这一缺陷。有限元分析可有效的指导家具结构设计，提升检测效率，大幅降低检测成本，助力实现无损检测。有限元分析(FEA)利用数学近似的方法对真实的载荷工况进行模拟，并能够通过形变和应力云图显示对模拟结果进行分析。该方法被广泛应用于土木工程、桥梁与建筑、航空航天、机械设计等诸多领域，为空间和结构的优化、强度和耐久性的提升以及突发情况的预警带来帮助。近些年来，诸多研究表明[3-4]，基于有限元分析能很好的模拟家具力学性能试验并能够为家具结构设计提供指导。

重组竹指由竹束或竹束片为构成单元，按顺纹组坯、胶合压制成的板方材[5]。重组竹物理力学性能优越、结构稳定、原材料丰富，诸多文献和市场研究结果表明[6-9]，近些年来重组竹家具所占市场份额越来越高，与木材相比，重组竹强度更高，具有良好的刚度，表面硬度、尺寸稳定性和环保性能更优，重组竹家具受到更多家庭和企业的欢迎。作为家具制造的原材料，重组竹被视为新型硬木，其广泛使用能够大大降低家具行业对木材资源的依赖，缓解国内木材短缺现状。

2 家具结构强度理论分析

2.1 试验方法

图1 床铺面集中静载荷试验方法Fig.1 Schematic diagram of concentrated static load test of bed surface

国家标准GB/T 10357.6-2013 《家具力学性能试验 第6部分：单层床强度和耐久性》中对床铺面进行的强度试验有3个，分别为床铺面均布静载荷、床铺面集中静载荷和床铺面冲击试验[10]。床铺面均布静载荷主要测量铺面在7天的均布加载后铺面中心下沉量，据此考察铺面在长时间铺设床垫、被褥后，铺面承载能力的变化，实木铺面在恒定载荷的作用下，通常会发生应变随时间逐渐增大的现象[11]，但这个过程较缓慢，且发生铺面断裂的风险较低。铺面集中静载荷试验要求在床铺面中心通过200 mm加载垫垂直向下施加1 100 N力，铺面不应断裂、紧固件不应松动、零部件不应磨损变形。床铺面冲击试验要求以25 kg冲击模块以140 mm的冲击高度冲击铺面中心和铺面薄弱处，铺面不应断裂、紧固件不应松动、零部件不应磨损变形。根据对日常检测结果的规律总结，3个床铺面试验中，最容易发生铺面破坏现象的是床铺面集中静载荷试验，因此研究选择GB/T 10357.6-2013中床铺面集中静载荷试验的方法设置试验条件，试验方法如图1所示。

2.2 材料力学性能分析

与研究相关的3种材料分别为松木(床铺面)、重组竹(床铺面)、硬质PVC(加载垫)。

查阅相关资料[8]，得到松木的抗弯强度约为65 MPa，但木材是天然非均质材料，受木材缺陷、应力集中和干燥的影响，其容许应力会产生相应折减，木材容许应力折减应考虑的因素包括：

(1)木材变异K1；(2)载荷的持久性 K2；(3)木材缺陷K3；(4)干燥的缺陷K4；(5)应力集中K5；(6)超载系数K6。

各因素对作用于松木抗弯强度的折减系数如表1所示。

表1 各因素对应折减系数

实际容许应力应通过公式2-1和2-2计算：

[σ]=σ12×K

(2-1)

K=K1×K2×K3×K4/(K5×K6)

(2-2)

公式中[σ]为实际容许应力，σ12为抗弯强度，K为总的折减系数，K1-K6为各因素对应的松木抗压强度的折减系数。根据2-1计算得出折减系数K=0.21，容许应力[σ]=13.6 MPa。

根据南京林业大学的束必清等人对重组竹力学性能及设计强度取值研究[12]，重组竹抗弯强度标准值σ12为172.1MPa，材料折减系数K为0.193，根据公式2-1，实际容许应力[σ]为34.2 MPa。

查阅相关资料[13-15]，材料的力学性能参数如表2和表3所示。

表2 松木和重组竹的力学性能参数

表3 硬质PVC的力学性能参数

图2 松木床铺面Fig.2 Pine wood bed surface

图3 加载垫Fig.3 Loading pad

由表2可以看出，抗弯容许应力更大的重组竹相比松木具有更好的强度。根据刚度计算公式，K=EI，其中K为材料的抗弯刚度，E为材料的弹性模量，I为截面惯性矩，由表2可以看出，弹性模量较大的重组竹也具有更好的刚度。

3 静载荷下的家具结构强度有限元分析

选用如图2所示松木实木床作为研究对象，基于三维CAD软件SolidWorks对床铺面、床框架和加载垫进行建模和装配，运用有限元分析软件Ansys Workbench对模型进行边界条件约束和力值加载，分析床铺面的变形和应力分布情况，结合分析结果调整床铺面结构和用材，在保证产品使用安全和舒适度的情况下，优化家具结构，以期达到结构强度和节约用材的最佳平衡。

3.1 模型建立

GB/T 10357.6-2013规定铺面集中静载荷使用200 mm加载垫，该加载垫为边长200 mm×200 mm的扁方形刚性物体，底面边沿及侧棱倒圆半径为12 mm。通过SolidWorks软件建立模型如图3所示。

图4 床铺面和框架简化模型Fig.4 Simplified model of a bedstead

对松木实木床进行测量，床长为2 000 mm，床宽为1 020 mm，铺面由17根宽度95 mm，厚度20 mm的松木板条组成，2个板条间间距为24 mm，板条首尾两端搭接于床框架上，搭接距离均为28 mm，通过8 mm沉孔螺钉穿透床铺面拧入床框架。床框架由床腿支撑，外侧和外框固定，两端和床屏固定，左右两根床框架采用长2 000 mm，宽28 mm，厚40 mm的松木方材构成。根据以上测量尺寸，对铺面和床框架进行简化建模如图4所示。

3.2 模型导入

如图5所示，将完整铺面模型导入Ansys Workbench，加载垫位于铺面中心，完整跨过中心板条并和中心左右两块板条产生接触，可见实际受力部位为最中心的3块铺面板条，为了提高计算机运算效率，可对模型进一步简化，如图6所示。

图5 铺面完整分析模型Fig.5 Complete analysis model of bed surface

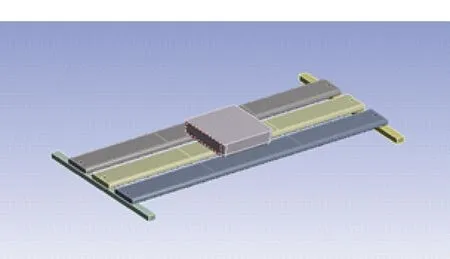
图6 铺面简化模型Fig.6 Simplified model of bed surface

图7 网格划分图Fig.7 Diagram of finite element grids

3.3 材料属性的设置

将模型导入后，在Ansys Workbench中设置材料参数，与研究相关的3种材料分别为松木(床铺面)、重组竹(床铺面)、硬质PVC(加载垫)。材料的力学性能参数如表2和表3所示。

3.4 网格划分

研究采用四面体网格划分法，对局部网格进行加密，图7为研究中的网格划分图，共产生228 380个单元以及348 082个节点。

3.5 设置约束条件和加载力

根据标准要求的试验条件，设置床框架外侧面、螺孔内侧面为固定约束，同时在加载垫上表面施加1 100 N垂直向下的力。

3.6 求解分析

为了方便分析，现对图7中3块板条进行编号，从左至右依次为1、2、3号。

床铺面在垂直地面方向产生形变的结果如图8所示。床铺面最大变形为5.89 mm，发生在1号板条的右侧和3号板条的左侧。此外，3块板条端部、1号板条左侧和3号板条右侧均发生上翘，上翘的最大幅度为0.49 mm。

床铺面等效应力的分析结果如图9所示，图中可见最大应力位于螺孔周围，这是由于约束条件的简化设置而产生的应力奇异点，即在求解受力体的应力函数时出现应力无穷大现象。从图中还可发现，应力集中在铺面板条中部的上表面和下表面。

图8 床铺面在竖直方向产生的形变Fig.8 Deformation of bed surface along the longitudinal direction

图9 床铺面等效应力Fig.9 Equivalent stress on bed surface

将板条中部上下表面的应力情况单独分析。如图10所示，左侧为板条中部上表面的等效应力图，右侧为板条中部下表面的等效应力图。上表面等效应力最大值为14.8 MPa，分布在加载垫4个角部对应的位置，等效应力平均值为6.2 MPa。下表面等效应力最大值为11.6 MPa，等效应力平均值为7.0 MPa，应力分布呈现出由内至外逐渐减小的趋势。由此可见，板条上应力最大值在1号和3号板条的上表面。

图10 板条中部上、下表面的等效应力Fig.10 Equivalent stress on upper and lower surfaces of the middle segment of a plank

床铺面板条的安全系数使用公式3-1计算:

n=[σ]/σ

(3-1)

其中n为安全系数，σ为材料的最大等效应力，[σ]为实际容许应力。研究中床铺面最大等效应力为14.8 MPa，松木实际容许应力为13.6 MPa。计算得出安全系数为0.91，其强度无法满足床铺面的使用要求。

4 床铺面的结构优化设计

为了使床铺面强度满足使用要求，应增强床铺面的强度，提高安全系数。增强床铺面强度常用的方法有以下2种：

(1)在床铺面下增加中床梃，如图11所示；(2)更换力学性能更好的材料，如重组竹材。

4.1 增加中床梃后的有限元分析

为兼顾构建设计的标准化，研究使用的中床梃的长度和宽度与床框架保持一致。分别对6组不同厚度的中床梃进行分析比对。6组中床梃所用厚度分别为15 mm、25 mm、35 mm、45 mm、55 mm、65 mm， 长度均为2 000 mm，宽度均为28 mm。中床梃两端固定约束于前后床屏上，铺面与中床梃接触但不固定。通过有限元分析计算，选择最合适的中床梃厚度。

分析比对计算简化模型如图12所示，设置中床梃的两端固定约束，其他约束和加载设置同上。

图11 铺面板条下增加中床梃Fig.11 Central axis added below the planks on bed surface

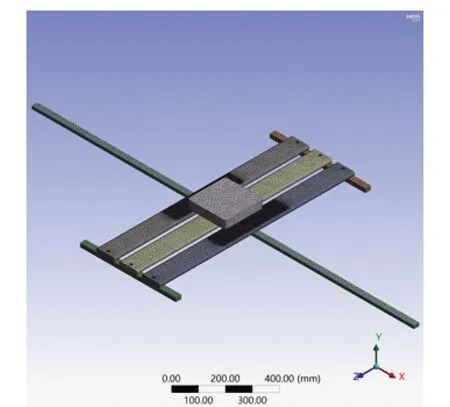
图12 板条下方设置中床梃的简化模型Fig.12 Simplified model of central axis added below the planks

由3.6的分析可知，板条上应力最大值在1号和3号板条的上表面，为了提高计算效率，不再对2号板条进行计算分析。使用15 mm、25 mm、35 mm、45 mm、55 mm和65 mm 6种厚度中床梃，对应的铺面板条应力计算结果如图13所示。

图13 增加不同厚度中床梃后对应的应力云图Fig.13 Stress contours with central axis of different thicknesses

增设6种厚度中床梃后，对应的最大等效应力和铺面安全系数分别如表4、图14和图15所示。

表4 增设不同厚度中床梃对应的最大等效应力和铺面安全系数

图14 最大等效应力随厚度的变化Fig.14 Variation of maximum equivalent stress as the thickness of central axis increases

图15 安全系数随厚度的变化Fig.15 Variation of safety factor of bed surface as the thickness of central axis increases

由计算结果可知，在铺面下增设中床梃能够有效提升床铺面强度；随着中床梃厚度的增加，床铺面最大等效应力逐渐降低，安全系数逐渐升高。当中床梃厚度达到35 mm时，安全系数为1，在理想状况下刚好满足使用要求。因此，增设长度2 000 mm、宽度28 mm、厚度35 mm的松木中床梃能够在解决铺面强度不足问题的同时，最大限度节约用材，达到节约用材和安全使用的最佳平衡。

但在实际使用中，安全系数为1时通常无法满足使用要求。为避免过载产生的安全风险，可使用厚度45 mm、55 mm或65 mm的中床梃，铺面的安全系数分别可达1.07、1.16和1.25。

4.2 使用重组竹后的有限元分析结果

使用重组竹作为铺面材料求解得到的结果如图16和图17所示。

图16和图17分别为重组竹铺面的变形结果和应力结果。结果显示，铺面上最大等效应力为10.8 MPa，同样分布在铺面上加载垫4个角部对应的位置，等效应力的平均值为5.2 MPa；铺面的最大变形为3.5 mm，发生在1号板条的右侧中部、2号板条的中部和3号板条的左侧中部，板条变形的平均值为2.2 mm。根据该文材料力学分析部分可知重组竹的抗弯容许应力为34.2 MPa，由安全系数计算公式3-1计算得出，重组竹铺面的安全系数为3.16。

图16 重组竹铺面在竖直方向上产生的形变Fig.16 Deformation of bamboo scrimber bed surface along the longitudinal direction

图17 重组竹铺面上表面应力云图Fig.17 Stress contour on bamboo scrimber bed surface

表5为相同铺面结构使用不同铺面材料的板条变形、等效应力和安全系数的对比表。

表5 不同铺面材料的有限元分析结果

从表5中可以看出，使用重组竹代替松木作为铺面板条能够有效提升铺面强度，重组竹在主要受力部位的使用能够显著提升床的结构安全性。

使用重组竹的另一优势在于，相同强度条件下重组竹家具更加轻便。表6为经有限元计算得出安全系数同样为0.91时，相同结构的松木铺面和重组竹铺面的材料使用情况。

表6 安全系数同为0.91的不同材质铺面的材料使用情况

从表5中能够看出，使用重组竹作为床铺面能显著降低铺面的体积，铺面的总质量也有了一定的减轻，因此，重组竹作为家具材料使用，能够在保证强度相同的条件下使家具更加轻便、简洁。

5 结论

运用ANSYS有限元分析软件对家具结构强度检测中发现的普遍问题进行理论分析，并选取松木床作为研究对象，根据家具力学性能国家标准的试验方法，对床铺面集中静载荷试验进行了有限元模拟。结果表明：通过有限元分析，选用改变床结构和换用重组竹材料2种方法进行强度优化设计，均可提升床铺面安全系数，2种方法均有较好的强度优化效果。此外，使用重组竹作为家具材料能够使家具在不失强度的情况下更加简洁轻便，重组竹的广泛使用也能够缓解国内木材短缺的现状。