温度对混凝土比热容的影响试验研究

张 冉，张秀崧，童富果，刘 畅

(1.三峡大学 水利与环境学院, 湖北 宜昌 443000;2.中水北方勘测设计研究有限责任公司， 天津 300222)

混凝土比热容是大坝温控仿真研究中的必要参数，其大小受混凝土组成成分、温度等因素影响[1-2]。根据朱伯芳[3]院士给出的国内外若干常规混凝土坝及碾压混凝土坝的热性能数值表，混凝土的比热容在温度变幅不大的情况下可近似的看作常量。肖照阳等[4]在进行白鹤滩输水系统进水塔底板的混凝土温控仿真分析时，将混凝土的比热容取为多年平均温度对应的比热容，认为其比热容不随温度变化。王晓峰等[5]等在进行某重力坝温控仿真分析时，将混凝土比热容取为常数。段寅等[6]在进行乌东德拱坝温控优化研究中，将混凝土比热容看作不变值。

然而，在实际工程中，受极端天气影响，气温日变化幅度较大，例如，我国北方局部区域气温日变幅可达35℃，因较大的昼夜温差引起的冻融循环破坏，导致混凝土内部出现较大的温度梯度[7-8]。在进行大坝温控仿真分析时，仍将混凝土比热容看作常量将不能满足实际工况的客观需求。赵维霞等[9]在试验中测得多孔膨胀珍珠岩混凝土在高温时的比热容，其比热容随温度的升高而非线性增大。郑文忠等[10]根据试验进行反演分析测得活性粉末混凝土在高温时其比热容随温度的升高而增大。许多专家学者[11-12]也对混凝土比热容随温度的变化进行了研究，对于高温条件下的试验研究较多，而对负温条件下混凝土比热容的研究较为有限，无法满足实际工况中大坝温度变幅情况，其比热容不能直接用于大坝温控仿真分析。

鉴此，本文首先基于混热法提出了一种积分计算混凝土比热容的方法，该方法将热交换中材料温度变化所历经的每个温度时刻对应的比热容都考虑进热平衡方程，然后通过测试混凝土各组分(砂、碎石、水泥石)在热交换中的温度变化数据换算得到其各自在不同温度条件下的比热容。对混凝土各组分(砂、碎石、水泥石)在不同条件下的比热容进行二次曲线拟合得到各组分在温度范围为-30℃～40℃间的拟合公式。最后根据混凝土的加权累加原则提出来一个考虑温度和配合比影响的混凝土多元回归模型，并对模型的有效性进行了验证，该模型为大坝混凝土温控仿真计算分析提供了数据参考价值。

1 混凝土比热容试验测试

1.1 试验原理与方法

比热容[13]为单位物质在温度变化过程中，每升高或降低1℃时吸收或释放的热量，通常使用符号C表示，其数学表达式为：

Q=CmΔT

(1)

式中：Q为温度升高或降低ΔT所需的热量，J；C为物质的比热容，J/(kg·℃)；m为质量,kg；ΔT为物质温度上升或下降的量，℃。

热平衡法是测定材料比热容常用的方法之一，该方法简单易行且换算比热容值直观明了，是一种较好的比热容测定方法。热平衡法又称混热法，根据热平衡原理，即将两个不同温度的物质混合在一起，充分吸放热以后达到热平衡，物质吸收的热量Q吸等于另一物质放出的热量放Q放，最终各物质温度将相同。由于水的比热容具有稳定、随温度变化规律相对确定的特点，较为适合用作测定材料比热容的标准物质，可以保证所测混凝土材料比热容的准确性。因此本文将水选作标准物质，将待测材料与水混合，根据记录热交换过程中材料与水各自的温度变化，通过计算可得待测材料在不同温度条件下的比热容值，计算公式为：

CxmxΔTx=CwmwΔTw

(2)

式中：Cx为待测材料的比热容，J/(kg·℃)；Cw为水的比热容，J/(kg·℃)；mx为待测材料的质量，kg；mw为水的质量，kg；ΔTx、ΔTw分别为材料与水混合前后各自的温差，℃。

在待测材料与水混合后，两者从混合前的初始温度到热平衡时的最终温度，在温度变化过程中，不同温度时刻所对应的待测材料比热容是不同的。因此，在利用式(2)热平衡方程进行比热容计算时，为了更准确的计算待测材料在不同温度下的比热容，本文将材料从混合前初始温度T0到热平衡时的最终温度Th过程中所经历的每一个温度时刻的比热容都考虑进热平衡方程。此处利用积分原理将材料在热交换中温度变化历程划分为多个阶段，进行积分，其示意图见图1。

图1 比热容变化积分示意图

将待测材料的比热容Cx在热交换中各温度变化阶段变化情况充分考虑进热平衡方程后得到其改进的热平衡方程，其数学表达式为

(3)

1.2 试验测试系统

(1) 试验仪器：系统试验装置主要由保温桶、恒温恒湿箱、温度传感器及温度采集程序组成，保温桶外包裹石棉、绝热纸以减少热交换过程中保温桶与空气接触造成的热量损失，提高试验精度，其保温桶示意图见图2。

图2 试验保温桶示意图

(2) 测试系统考证：鉴于在试验过程中，系统本身会存在一定量的热量损失，影响试验精度。根据补偿热量修正法[14]，利用混热法进行试验时，每组试验中水的初始温度满足以下条件：当材料为正温时(高于 0℃)，材料与水混合达到热平衡后的最终温度Tf高于环境温度；当材料为负温时(低于0℃ )，终温Tf低于环境温度。试验通过调节混合系统的比例，令混合过程中系统与环境之间交换的正负热量量值相等，则可认为系统在整个热量交换过程中向环境散失的热量为零，从而对试验过程中的热量损失进行修正。且使热平衡时最终温度Tf始终为正温，可有效避免水在高温和负温环境下发生相变从而降低试验精度。

利用混热法测量常压下温度变化范围为15℃～50℃的纯净水比热容值，即将两种不同水温的水混合，根据所记录的水从初始温度到热交换完成达到热平衡时的温度变化数据，采用式(3)换算即可获得水随温度变化的比热容试验值。为验证试验结果的准确性，图3中给出了本文比热容试验值与文献[15]中所列出比热容的对比偏差情况。

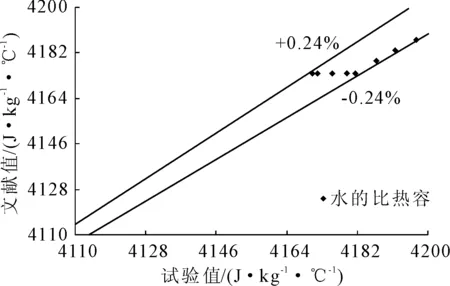
图3 水的比热容变化

由图3可知，水的比热容会随温度变化而发生一定波动，与文献值相比二者变化趋势相近，相对误差为0%～0.24%，吻合度较好。对比结果表明，该测试系统的精度满足试验要求，可继续用于测取混凝土材料的比热容。

1.3 试验材料与方案

(1) 试验材料

采用过筛后粒径0.075 mm～0.500 mm天然细砂和粒径5 mm～10 mm碎石，华新牌P.O.42.5普通硅酸盐水泥，纯净水，龄期60 d养护完成的水泥石，水泥净浆配比见表1。

表1 水泥净浆配合比

混凝土级配选择以三峡大坝的混凝土配合比为基础进行调整，经过多次试验调整后所选用混凝土配合比见表2。

表2 混凝土配合比

水泥与水混合产生的水化反应将会改变其各自的热性能，用水泥净浆硬化后形成的水泥石进行试验可有效降低水泥与水之间水化反应的影响。由于碎石、水泥石本身体积较大在热交换中不能够充分的吸放热，而同一物质的比热容一般不随质量、形状的变化而改变[16]，故分别将其研磨成粉末进行试验。考虑材料水分含量对试验结果有所影响，将所有试验材料用烘干箱烘干24 h以上至恒重装入封口密封袋备用。

(2) 试验方案

③ 将所测得的各温度数据代入式(3)计算可得各待测材料在不用温度时刻的比热容Cx。

2 温度对混凝土比热容的影响研究

2.1 混凝土各组分在不同温度条件下的比热容

根据公式(3)计算得到混凝土各组分(砂、碎石、水泥石)比热容随温度变化关系见图4。从图4中可以看出，混凝土各组分(砂、碎石、水泥石)的比热容均随温度的升高而增大，三者变化趋势一致但也稍有差异。 相同温度增量下，砂的比热容随温度的升高呈现平稳上升趋势，而碎石的比热容变幅先增大后逐渐变缓，水泥石比热容的变幅更大，受温度变化的影响更为显著。

图4 混凝土各组分的比热容随温度变化规律

对上述试验测得的混凝土各组分(砂、碎石、水泥石)比热容值进行二次曲线拟合，得到在温度范围为-30℃～40℃间混凝土各组分(砂、碎石、水泥石)的比热容回归方程为：

Cs=0.0012T2+2.4394T+892.35

(R2=0.992 8)

(4)

Cg=-0.0291T2+2.5471T+928.3

(R2=0.977 6)

(5)

Ccs=-0.0028T2+2.1216T+888.84

(R2=0.979 6)

(6)

式中：Cs、Cg、Ccs分别为砂、碎石、水泥石的比热容，J/(kg·℃)；T为混凝土各组分材料的温度，℃。

根据各回归方程计算了20℃时混凝土各组分(砂、碎石、水泥石)的比热容与文献所列比热容对比情况，见表3。

表3 混凝土各组分在20℃下的比热容

由表3可知，20℃下混凝土各组分(砂、碎石、水泥石)的比热容与文献所列值相比，试验所得骨料的比热容小于水泥石的比热容，而文献所列骨料的比热容大于水泥石的比热容，其差异性可考虑为砂和碎石的比热容一般受内部化学成分影响大，根据不同地区所选取的不同砂性和不同种类岩石其内部所含化学成分的比热容不尽相同，但试验值与文献所列值整体相比较为接近。试验结果表明，用混热法来测定材料的比热容满足本文试验的精度要求，在操作上方便易行，是一种较好的测定材料比热容的方法。

2.2 温度对混凝土比热容的影响

混凝土作为一种人工复合材料，不同配合比混凝土的比热容差异较大。根据混凝土比热容的定义，混凝土的比热容满足各组分比热容加权平均累加原则，但应将其应用于混凝土凝结硬化后的不同相(砂、碎石、水泥石)[19]，其数学表达式为：

Cp=Csws+Cgwg+Ccswcs

(7)

式中：Cp、Cs、Cg、Ccs分别为混凝土、砂、碎石、水泥石的比热容，J/(kg·℃)；ws、wg、wcs分别为砂、碎石、水泥石的质量百分比(wcs=1-ws-wg)。

对上述计算结果进行多元回归拟合分析，可得在本文水灰比下不同骨料配比的混凝土比热容在温度范围为-30℃～40℃间随温度变化的数学模型：

Cp=a1T2+a2T+a3

(8)

式中：T为混凝土的温度，℃。

a1=0.04ws-0.0263wg-0.0028；

a2=0.3178ws+0.4255wg+2.1216；

a3=3.51ws+39.46wg+888.84。

该模型考虑了温度及骨料配比对混凝土比热容的影响，在进行大坝温控仿真计算时，可以对温度范围为-30℃～40℃间不同骨料配比的混凝土比热容进行有效预测，能够较好地反应不同骨料配比的混凝土比热容随温度变化的规律。

为验证上述模型的准确性，将文献[20]中的混凝土配合比代入上述模型中，计算得到混凝土比热容在不同温度条件下的模型预测值，将其与文献中所列的同一配合比下的混凝土比热容相比较，结果见表4和图5。

表4 不同温度下的混凝土比热容

图5 同一配合比下，混凝土比热容的比较

从表4和图5可知，混凝土的比热容与温度呈正相关，并且随温度的升高而非线性递增，速率逐渐变缓。同一配合比下，混凝土比热容的模型预测值与文献所列的值相比，相对误差在0.0%～3.2%，吻合度较好。结果表明，该模型对不同配合比下混凝土比热容随温度变化的预测具备有效性。

3 结 论

本文基于热平衡原理测取了砂、碎石、水泥石在不同温度条件下的比热容，研究结果表明：

(1) 混热法测定材料的比热容换算比热容值直观明了、试验装置简便，在经过温度修正满足试验精度的前提下是一种较好的测定比热容的方法。利用积分原理将材料的比热容在每个温度阶段的变化情况考虑进热平衡方程能够更加准确的计算材料的比热容。

(2) 砂、碎石、水泥石的比热容与温度呈正相关并随温度的升高而增大，变化速率逐渐变小。

(3) 混凝土的比热容满足各组分比热容加权平均累加原则，但应将其应用于混凝土凝结硬化后的不同相(砂、碎石、水泥石)。并推出了考虑温度和配合比影响的混凝土比热容模型，能够更好的预测不同配合比混凝土的比热容随温度变化的情况。

(4) 混凝土的比热容随温度的升高而增大，且在同一配合比下混凝土比热容的模型预测值与文献值所列值对比具有很好的相关度，吻合度较好，从而验证了该模型的有效性。