图像拼接算法发展综述

罗运，贺翔，丁诗婕

（四川大学计算机学院，成都610065）

0 引言

图像拼接是将两幅或者多幅具有重叠区域的图片，采用一定的方法进行融合从而获得更宽视野或者更高分辨率的图像处理技术。在实际应用中，图像拼接技术已经被广泛应用于医学成像、遥感技术、虚拟现实、手机全景等各领域。与此同时，为了获得更加自然的拼接图像效果，图像拼接必须要解决采样透视失真问题、伪影问题。图像拼接包含图像预处理、图像对齐（配准）和图像融合三个步骤，各研究学者从这几个子问题出发，研究算法并获得了比较不错的效果。

图像拼接技术主要有两个分支：基于像素到像素的直接方法以及基于特征的拼接算法[1]。因为基于特征的图像拼接技术在尺度、方向、投影缩减上具有更好的鲁棒性，因此成为了当今研究的热点。常见的特征提取算法有SIFT[2]、SURF[3]、PCA-SIFT[4]等。1997 年，Richard 等人[5]提出了一种严格控制输入图像序列，并且不限制拍摄运动的图像拼接方法。2003 年，Brown等人[6]基于不变特征提出了全自动全景图像拼接的模型，该模型在2007 年[7]得到改进。该文章首次提出一种比较完善的基于特征图像拼接流程，首先从输入图像中提取SIFT 特征，然后将图像拼接问题视作多图像匹配问题，找到无序图像集中的图像之间相互关系以进行全景图像识别，最后通过光束差法将有关联的图像进行融合获得无缝的高质量图像。由于SIFT 提取的特征点对较多，因此文章采用了RANSAC[8]方法进行筛除误匹配点以获得更好的匹配效果。

因为单应性变换能够解释较多场景下（旋转、相似等）两平面图像之间的变换关系，因此在图像拼接中被广泛采用。Brown 等人2003 年提出的全自动全景图像拼接就是基于RANSAC 过滤的特征点对得到的更强鲁棒性初始单应变换矩阵。但往往，唯一的全局单应矩阵得到的图像拼接效果不尽如人意，可能出现误对齐以致伪影问题的出现。很多学者基于此提出了效果较好的后处理方法，这些方法基于缝合线[9]或者图像切割进行优化，但这些后处理优化并不见得在所有场景都能适用。2011 年，JunHong Gao 等人[10]针对可以分为远处的后平面和以及摄像机扫出的地平面的图像，提出了图像拼接的双单应扭曲变换。2014 年，Julio Zaragoza 等人[11]为了避免误对齐以及过分依赖后处理和消除伪影，提出了尽可能投影（APAP）算法。该算法首次提出网格形变，首先建立Moving DLT 数学模型，然后解超定方程生成网格单应矩阵进行透视变换。这是网格多单应变换的首次应用，其有效地消除了伪影，但是没有限制网格数量也没有解决透视失真的问题。Che-Han Chang 等人[12]提出的基于保形差值的算法，能够解决透视失真的问题，但对于大视差情景，则需要结合APAP算法。后续的研究者从网格优化、多特征出发进行研究都获得了不错的图像拼接效果。本文将重点分析APAP 算法以及其衍生的相关算法。

1 单应性矩阵和Moving DLT

1.1 单应性矩阵

当拼接图像仅包含旋转或者各图像处于同一平面时，用单应性矩阵来表示它们平面物体的运动关系是恰当的。单应性矩阵是一个3×3 的矩阵。令x=[x y]T为图像I 中的一个像素点，x'=[x'y']T为具有重叠区域的与x 相匹配的像素点。则两像素点其单应变换关系可以表示为：

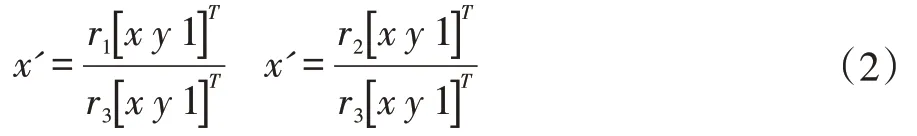
其中，rj为H 矩阵的第j 行。

1.2 Moving DLT

DLT 是一种从包含噪声匹配点对估计单应变换矩阵H 的基本方法。我们常用的匹配点对常采用SIFT特征点。

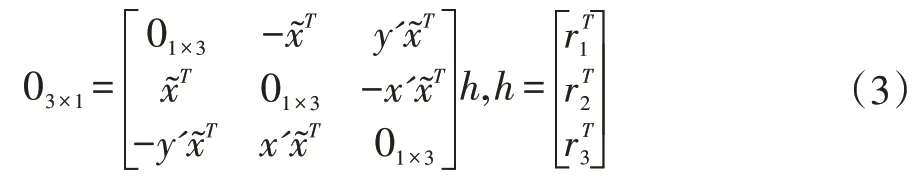
其中，h 是将H 向量化得到的向量。（3）式中只有两行式线性无关的。使αi为（3）矩阵中的前两行，以用来计算第i 个匹配点对{xi,x'i} 。给定一个估计h，‖αih‖是第i 个基准点的代数误差。DLT 使代数误差的平方和最小化。

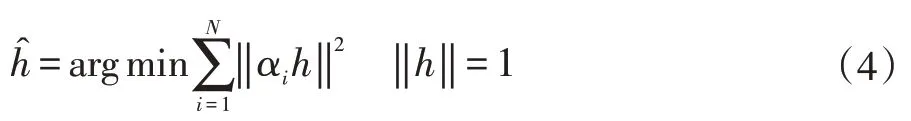
同样地，将所有的αi垂直叠加到一个新的矩阵A∈R2N×9。（4）式可以被重新定义为：

通过重建得到的估计一个H，原图像I 和目标图像I'之间任意点对的对应关系可以表示为：

为了避免数值精度问题，在DLT 计算之前，可以先对数据进行归一化操作，然后在执行前进行H 的去归一化。

上面描述了理想条件下的H 矩阵的估计，当视图I 和I' 不仅仅包含旋转关系或者不是处于同一平面时，采用一个基本的H 矩阵可能会产生误对齐或者视差错误。由此Moving DLT 被提出，通过使用依赖位置的单应性去变换每一个x*。

其中H*是通过加权问题估计得到：

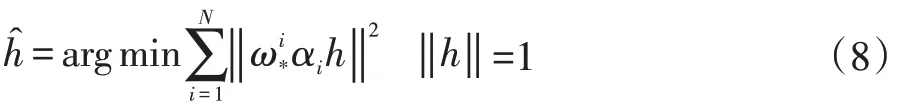
其中，距离x*越近将会赋予更高的权重，并由下列式子计算得出：

其中，σ是一个尺度参数，xi是源图像I 中第i 个点匹配{xi,x'i} 一半的坐标。直观上来看，式（9）分配了更高的权重给距离x*更近的点，因此，H*更好地遵循了点x*附近的局部结构。同时，因为x*在I 中是连续地移动，因此变换H*也是平滑地变化，这就产生了能够灵活适应数据的整体变形，同时又试图保证了投影的变化趋势。这也就是Moving DLT。

2 APAP算法及衍生算法

2.1 APAP算法

当两幅图像或者多幅图像不再满足上述的理想条件，用唯一的单应矩阵去估计变换关系，不可避免地会产生误对齐或者视差。为了避免这个问题，Julio Zaragoza提出使用Moving DLT 计算全局单应性矩阵，再按照一定规律将待对齐图像进行网格划分，依照网格权重进行对每个网格中的局部单应性矩阵计算，再按照局部单应性矩阵进行融合。它的算法步骤如下：

（1）在两幅待对齐图像中，提取SIFT 特征点；

（2）在得到的特征点中，使用RANSAC 算法剔除错误特征点；

（3）使用Moving DLT 估计全局单应性矩阵；

（4）采用一定的规律对带对齐图像进行网格划分，对网格中的特征点以及网格权重进行计算；

（5）根据步骤（4）得到的权重和全局单应性矩阵计算每一网格的单应矩阵。得到每一网格的局部单应矩阵。

（6）使用局部单应矩阵进行图像拼接。

APAP 算法能够解决待拼接图像不是完全旋转的情形，并且通过局部权重约束调整能够同时较好地对齐多幅图像。但是APAP 算法中，选择划分网格的数量以及解决透视失真的问题。在它的实验结果中，伪影得到明显解决，但直线扭曲，物体透视失真等问题依然显著。SPHP 算法则在解决透视失真的问题上有良好的效果。

2.2 SPHP算法

SPHP 算法提出了一种新颖的解决透视失真的方案。其通过将重叠区域的单应变换过渡到非重叠区域的相似变换，能够有效地解决透视失真的问题，对于大视差图像拼接，其可以通过结合APAP 算法能够获得比较自然的图像效果。其具体步骤如下：

（1）半投影变换

SPHP 算法首先通过线u=u1将R2分成两个空间：RH={(u,υ)|u≤u1} ，RL={(μ,υ)|u＞u1} 。其中，(u,υ)是待拼接图像原像素坐标(x,y) 通过单应矩阵变换而来的新坐标。u1用于将图像划分为两个区域，RH理解为重叠区域，RL为其他区域。

对于(u,υ)∈RH，直接用H 进行单应变换。对于(u,υ)∈RL，由于单应变换H 造成了比RH更大的面积失真，因此将单应变换替换为相似变换，以此来减少图像在形状和尺寸上的失真。同时为了保证变换的连续性以避免明显的拼接裂缝，必须要求对于分界线上所有的(u，υ)都满足S(u,υ)=H(u,υ)。

（2）C1外推

为了构建C1扭曲，SPHP 将RH拆分为两个空间：RT={(u,υ)|u1＜u＜u} ，RS={(u,υ)|u2≤u} 。RT可以视作一个将单应变换H 平滑过渡到相似变换的过渡区域。

因此整张待拼接图像被划分为三个区域，即：

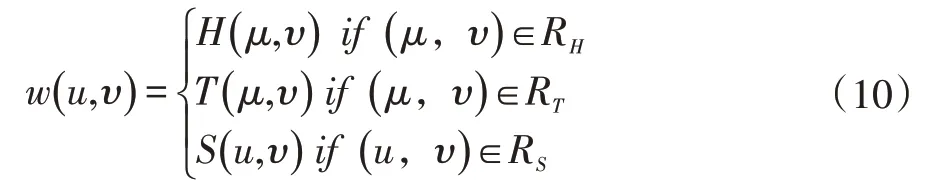
T(μ,υ)是定义在中间区域RT中逐渐改变H(μ,υ)到S(μ,υ)行为的函数。S(μ,υ)是定义在RS的相似变换。S(μ,υ)参数化如下所示：

其中，fx(u),fy(u),gx(u),gy(u)为未知函数。通过H(u,υ)和S(u,υ)进行进一步的简化：

其中Fx(u),Fy(u),Gx(u),Gy(u)包含未知函数，我们以Fx(u)为例，Fx(u)可以表示为以下形式：

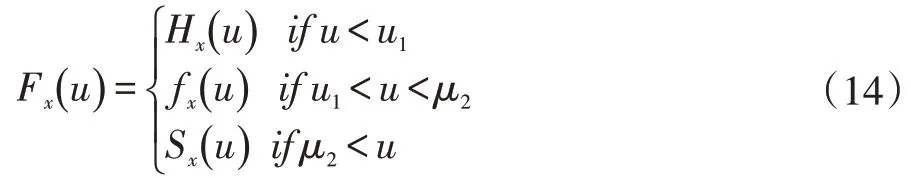
Hx(u),fx(u),Sx(u)分别来自H(μ,υ),T(μ,υ),S(μ,υ)步骤的求解。同理Fy(u)υ,Gx(u),Gy(u)。同时，为保证Fx(u)的连续，fx(u)也必须满足以下条件，即在u1,u2处函数连续，并且其倒数也要连续：

Fy(u)υ,Gx(u),Gy(u)同理，由此可以过渡变换T(μ,υ)。

（3）相似变换

非重合区域RS运用相似变换，并且结合前两个区域的变换，完成图像拼接。

SPHP 利用相似变换，极大地保留了图像的原有视角，减少了图像透视失真，同时为了获得更好的对齐效果，文章作者给出了结合APAP 算法的优化方案。

2.3 Line Meets APAP[13]算法

文章作者观察到在一些实际生活中，一些场景例如重复纹理图片或者人造建筑的同质区域，点特征可能不能维持较好的匹配效果。因此，将线特征加入APAP 算法，既能保持图像之间的强对应关系，也能维持图像的结构属性。

（1）线关系

（2）点特征与直线特征结合

通过简单的矩阵连接，式（5）中的A变为A∈R2(N+M)×9，并且通过新的矩阵A 估计全局单应矩阵。

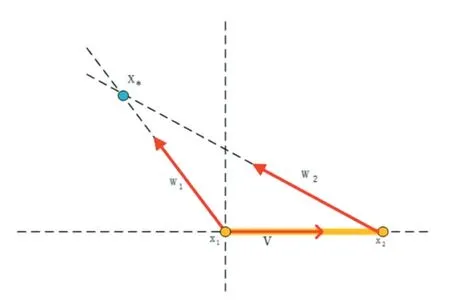
图1

（3）线的权重计算

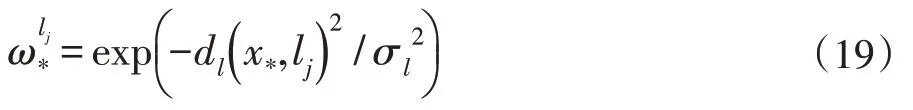
其中，σl是一个尺度参数dl(x*,lj) 表示点x*与直线lj最近的距离。

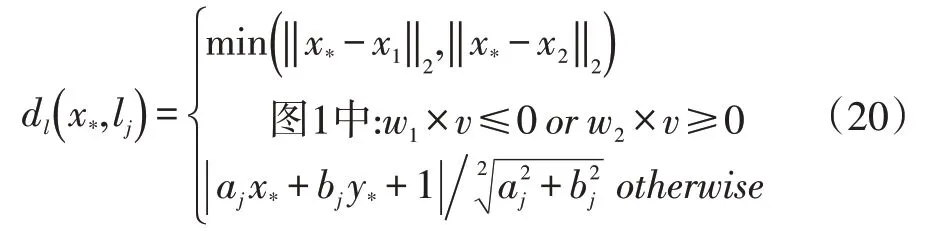
其中x1,x2为直线lj的两端点。

（4）平衡参数λ

该算法因引入了点和线两种特征，必须考虑如何平衡这两者来获得更高的图像拼接质量。该文作者提出了平衡参数λ来保持点和线的最佳平衡关系——通过最优化对应点和线的二次投影误差来实现。

对于点：

其中，d(.,.)表示欧氏距离，H 是估计的单应性矩阵，Ψ(·) 是一个索引映射。

对于线：

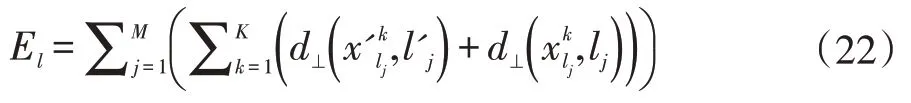
其中，d⊥表示线段的投影距离。文章通过来计算最终的二次投影误差。通过E值，就可以找到合适的λ值。

通过点和线特征的结合，该算法对于图像对齐和视差问题都具有强鲁棒性。

3 结语

图像拼接技术的核心步骤是图像对齐和图像融合。在不是理想条件约束下的图像拼接（图像仅包含旋转或图像处于同一平面），依靠不变特征以及多局部单应矩阵获得良好对齐效果的图像拼接技术值得肯定和研究。但同时也要注意到，应用场景是复杂的，图像拼接过程中出现的伪影、间隙、透视失真等问题要有效解决。例如对于特征点在某一区域较为稀疏，而在另外一区域则较为密集的情况，这样的图像拼接在对齐阶段必然效果很差，因此引入多特征进行约束。对于失真问题，SPHP 提出了结合相似变换和单应变换。APAP 算法作为网格形变的代表作，后续研究者基于其做了许多拓展，这些拓展从网格约束出发，都获得了不错的效果。在未来研究中，我们还可以在大视差、视频拼接、图像混叠问题着手。