行人与轿车正碰后卷绕型运动形态仿真研究*
王 征,李 旋,韩天园,刘永涛,袁立青,徐峰祥
(1.浙江交通职业技术学院,浙江 杭州 311112; 2.长安大学 汽车学院,陕西 西安710064; 3.湖北省军区数据信息室,湖北 武汉 430070; 4.武汉理工大学 汽车工程学院,湖北 武汉 430070)
0 引言
针对长头轿车(车辆前端具有突出的发动机室,且前端高度低于成人站立质心高度)碰撞行人的事故,现有研究主要围绕事故中行人损伤分析以及行人运动规律分析2个方面。段腾龙等[1]通过实际的事故案例验证PC-Crash在法医学鉴定中的应用价值;王清平等[2]对PC-Crash中轿车-行人事故重建参数敏感性进行分析,证明PC-Crash进行事故分析的可靠性;在此基础上,余超等[3]基于有限元分析乘用车前挡风玻璃角度对行人头部损伤影响;胡林等[4]基于PC-Crash仿真分析年龄因素对事故中行人下肢的损伤影响;李丹等[5]分析行人运动状态对行人损伤的影响;李骏等[6]再现了轿车碰撞行人事故过程,分析抛距与行人头部损伤的影响因素;杨济匡等[7]发现,事故中行人抛出运动形态主要由行人走向以及车辆前部结构决定;国外针对行人损伤分析以及行人运动规律亦进行大量研究[8-14]。
长头轿车与行人碰撞后行人出现卷绕型运动形态,目前针对行人卷绕型运动形态规律已有大量研究[6,9],文献[6]分析各个参数对行人抛距及行人头部损伤的影响,但未具体给出量化公式,文献[9]基于实际案例数据拟合行人抛距公式,但是未结合影响参数。因此本文基于PC-Crash软件和MADYMO多刚体仿真软件仿真分析长头轿车-行人碰撞事故中行人卷绕型运动形态规律,得出行人的分段抛距公式,同时研究碰撞车速、行人走向、车辆参数(前挡风玻璃倾角、发动机罩倾斜程度)对行人头部、胸腔的损伤影响,旨在为车辆主动安全设计以及行人保护提供参考。
1 实验方案与评价指标
本文研究长头轿车前部正中与行人发生碰撞,因此不考虑车辆碰撞点位置,假人身高设置为1.69 m,体重设置为68 kg,实验车辆标准参数采用现代accent07参数。路面与车辆的摩擦系数参考《道路交通事故车辆速度鉴定》(GB/T 33195—2016)设置为0.7,行人与路面的磨擦系数设置为0.6,且车辆均以最大制动力制动。
实验过程中,根据CIDAS数据库中2016—2019年的长头轿车碰撞行人的事故案例,结合研究内容对各个因素的范围进行设置。车辆速度范围为20~65 km/h,包括低、中车速;行人碰撞前的朝向根据车辆行驶方向,设置为0°,45°,90°,135°,180°,碰撞前的行人朝向如图1所示。前挡风玻璃的倾角为与Z轴的夹角,以标准车辆参数的基准设置在20°~45°范围内;发动机罩倾斜程度,通过斜面与水平面的夹角反映,设置在1°~10°。

图1 碰撞前的行人朝向Fig.1 Pedestrian orientations before collision
实验过程中通过分析碰撞后行人抛距、行人质心离地最大高度、行人旋转圈数、行人与车辆分离时行人姿态以及速度等信息分析行人卷绕型运动形态规律。连续3 ms最大加速度值用于评价胸腔损伤严重程度,加速度越大,损伤越严重;头部损伤指标(Head Injury Criterion,HIC)用于评价头部损伤严重程度,HIC值越大头部损伤越严重,HIC值1000作为安全界限,如式(1)所示:
(1)
式中:HIC为头部损伤指标;a(t)为头部的重心合成加速度,m/s2;t2,t1为任意2个时刻,ms。
2 模型建立与验证
2.1 模型建立
由于考虑2了车辆发动机罩、前挡风玻璃等结构属性,因此单一刚体结构模型不再适用,通过MADYMO多刚体仿真软件,在CIDAS实际事故数据的基础上,针对车辆前端,即前挡风玻璃、发动机罩、保险杠3个部分,分别用矩形椭球面表示,各个椭球之间用铰链连接。针对不同的事故,通过改变各个部件参数构建出事故车辆模型;行人模型采用PC-Crash内置的人体多刚体模型,该模型将人体部位,如头部、盆骨等视为刚体,共24个刚体,将关节视为铰接点,共15个铰接点,其内置的人体参数优化器可以设置包括身高、体重、速度在内的多个参数。
2.2 模型验证
选取CIDAS数据库中1起长头轿车-行人事故进行分析。轿车-行人碰撞后形态如图2所示,1位25岁男性由斑马线自南向北横穿道路,行至1/2位置处,与自西向东驶来的轿车发生碰撞,造成行人死亡。事故发生在晴朗天气、沥青路面下,路面干燥,碰撞时车辆速度为45 km/h。
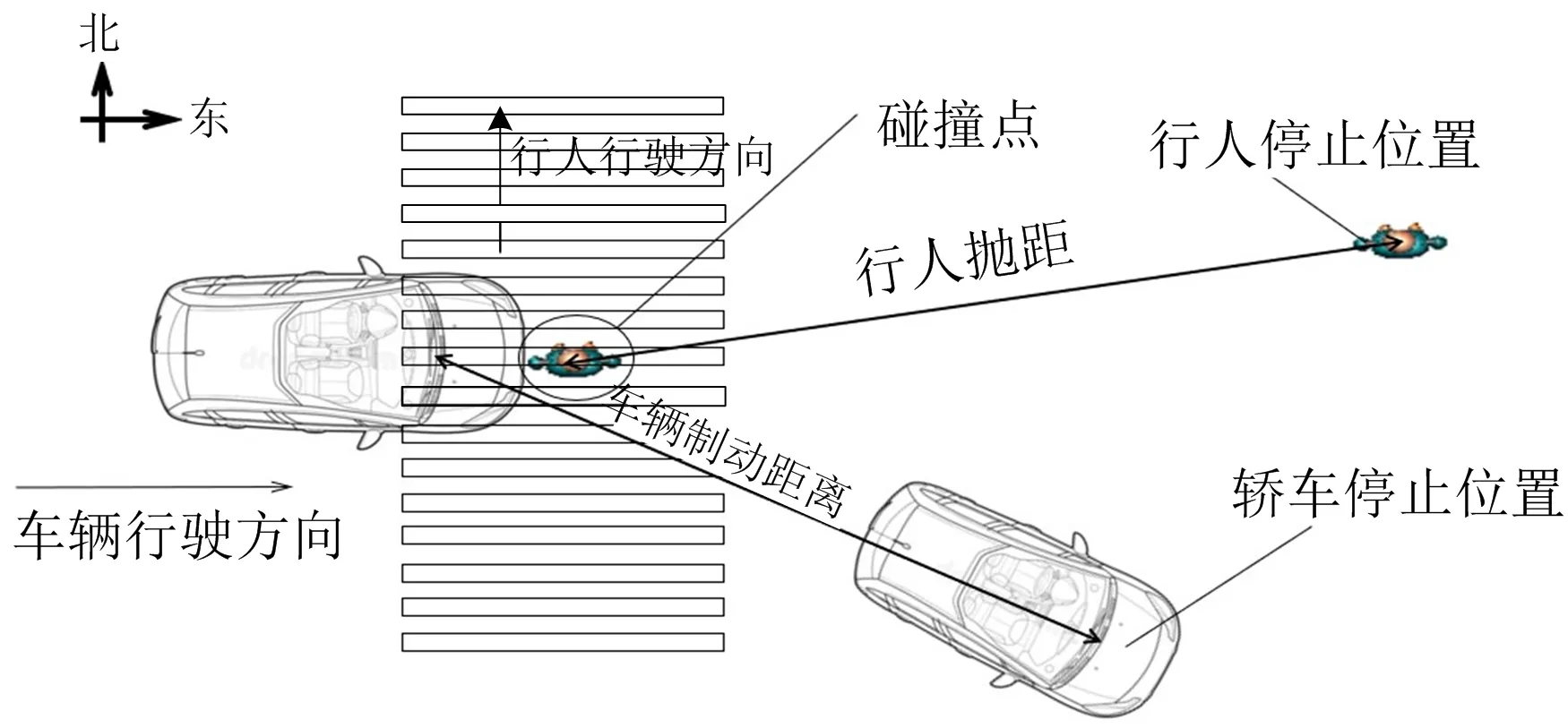
图2 轿车-行人碰撞后形态Fig.2 Pattern after collision between car and pedestrian
假设轿车碰撞到行人后才开始减速,人车相对停止距离、行人抛距实际结果与仿真结果对比见表1,误差均小于5%。

表1 实际结果与仿真结果对比Table 1 Comparison of actual results and simulation results
轿车与行人碰撞的对应关系如图3所示,t=55 ms时,车辆发动机罩边缘与行人大腿发生碰撞,行人的上肢由于惯性作用倒向发动机罩;t=145 ms时,行人的头部与前挡风玻璃发生碰撞,此时行人脱离车辆表面,被抛出后开始自由转动;t=1 420 ms时,行人的头部先与地面碰撞。最后,行人在地面上翻滚,头部、胸腔等身体部位与地面发生摩擦。

图3 轿车与行人的碰撞关系Fig.3 Collision relationship between car and pedestrian
对比行人与车辆的相对停止距离、行人抛距、碰撞对应关系和行人损伤等数据,结果表明,仿真数据与真实事故数据能够较好地吻合,据此验证行人与车辆模型的可行性和准确性。
3 实验结果与分析
3.1 卷绕型运动规律
行人与车辆分离时质心的速度大小以及分离时行人姿态决定人车分离后抛距的大小。行人与车辆分离时速度如图4所示,随着碰撞车速的增加,行人各走向下分离速度逐渐增大,最大不超过40 km/h,在35~45 km/h车速下有所下降,这是由于行人旋转圈数增加,与车辆碰撞次数随之增加,速度继续增大,分离速度保持增大的趋势,说明分离速度的大小主要取决于碰撞车速。通过多项式拟合,分别拟合出不同走向下的函数回归模型,决定系数R2均大于0.85,证明拟合得到的行人与车辆分离时质心的速度值可靠,如式(2)所示:
(2)
式中:v为车辆碰撞速度,m/s;v0,v45,v90,v135,v180分别为各个走向下分离行人时质心的速度,m/s;R2为决定系数。
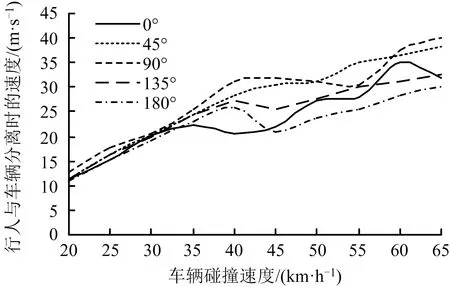
图4 行人与车辆分离时速度Fig.4 Speeds when pedestrian separating with vehicle
当碰撞车速超过35 km/h时,为简化行人落地后的运动过程,同时保留计算结果的准确性,行人在路面上的位移如图5所示,利用最小二乘法原理,拟合出行人与车辆分离时的速度vα与行人在路面上位移的指数函数公式。行人在路面上位移随着分离速度的增大而增大;不同行人走向下,随着分离速度的增加,行人位移增加速率不同,90°下行人位移增加最快,这是因为在90°下,行人落地姿态更容易发生翻转。分析发现,行人在路面上的位移主要与分离速度有关,即与碰撞时车辆速度有关,同时在一定程度上取决于行人与车辆分离时的姿态。

图5 行人在路面上的位移Fig.5 Pedestrian displacement on road surface
行人抛距简化组成如图6所示,S2为行人与车辆分离后落地前的位移,S3为行人落地后的位移,结合式(2)得到行人的抛距如式(3)所示:
(3)
式中:S为行人抛距,m;S1为碰撞开始到行人与车辆分离时,行人质心运动的位移,m;v为车辆碰撞前的速度,m/s;h为行人与车辆分离时质心高度,m;θ为发动机罩倾斜程度,°;μ为行人与路面的摩擦系数;g为重力加速度,m/s2;k1,k2分别为拟合vα与行人在路面上位移的指数函数公式拟合系数;m1,m2,m3分别为拟合vα与v多项式的拟合系数。

图6 行人抛距简化组成Fig.6 Simplified composition of pedestrian throw distance
20~65 km/h车速范围内,行人抛距结果对比如图7所示。在行人朝向为90°的情况下,多项式拟合得到的行人抛距曲线,虽然能较好地反映拋距变化趋势,但对应每个碰撞车速下的拋距值与实际抛距值存在较大误差,当车辆碰撞速度为20 km/h,此时抛距计算误差达到20.6%,计算车速每增加5 km/h的抛距误差,发现平均误差在10.2%;本文提出的分段计算公式不仅能较好地反映抛距变化趋势,并且在2个分段范围内均能较好地拟合实际抛距,平均误差为4.23%,验证了本文得到的分段抛距公式的准确性。

图7 行人抛距结果对比Fig.7 Comparison of pedestrian throwing distance
3.2 不同发动机罩倾斜程度以及不同车速对车速的影响
不同发动机罩倾斜程度对应不同车速下的行人抛距如图8所示,行人抛距随着车速的增大而增大,这与文献[15]的结论相吻合;同一车速下,随着θ的增大,抛距逐渐减小,此时cosθ减小,行人与车辆分离后,垂直方向上的动能增加,水平方向上的抛距随之减小。
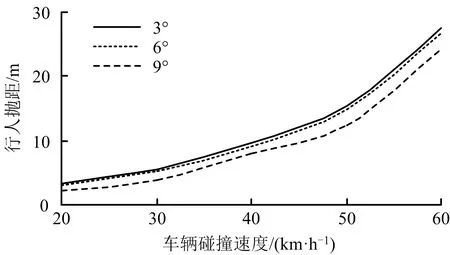
图8 不同发动机罩倾斜程度对应不同车速下的行人抛距Fig.8 Pedestrian throw distance under different tilt degrees of engine hood and car speeds
3.3 不同前挡风玻璃倾角以及不同行人走向对行人损伤的影响
设置行人走向为0°,90°,180°,对应不同的前挡风玻璃倾角分别进行仿真。根据CIDAS数据库碰撞数据统计,选择40 km/h车速进行损伤对比实验。头部HIC值如图9所示,当行人走向为180°时,头部损伤严重程度最高,此时行人撞击部位为后脑,较为脆弱,且头部HIC值随着行人走向角度的减少而减少,在0°时头部损伤程度最低,此时行人撞击部位为头部前侧,强度较高;随着前挡风玻璃倾角的增大头部HIC值逐渐下降,这主要是因为倾角增大,垂直于前挡风玻璃方向力减小。

图9 头部HIC值Fig.9 Values of HIC at head
胸腔连续3 ms最大加速度值如图10所示,车速在40 km/h时,改变行人走向以及前挡风玻璃倾角,行人的胸部损伤风险始终低于人体极限,这与文献[15]中的结论相符合。同一车速下,行人走向为0°时,胸部损伤风险较大,这是因为此时行人胸部正对发动机罩,随着行人走向角度的增大,胸部损伤风险明显下降,此时胸部并不是主要碰撞位置;同一走向下,随着前挡风玻璃倾角的增大,胸部损伤风险增大,这与头部损伤分析结果相吻合,此时水平加速度减小,即头部损伤减小,胸部向下的加速度增大。

图10 胸腔连续3 ms最大加速度值Fig.10 Maximum acceleration of thoracic cavity for consecutive 3 ms
4 实际案例验证
为同时验证抛距模型以及拟合的行人动力学响应值,按照车辆、行人数据,从CIDAS数据库中选取3例真实长头轿车-行人的案例进行事故重建,事故标准:1)车辆与行人碰撞时的车速为40 km/h;2)碰撞瞬间行人走向为0°,90°,180°;3)事故车辆前挡风玻璃倾角20°,30°,40°;4)行人身高大于1.5 m。数据误差均在±5%以内。实际案例中由于无法得到头部HIC值以及胸腔连续3 ms最大加速度值,通过PC-Crash仿真对事故进行还原。事故案例参数信息如表2所示,真实与仿真结果对比如表3所示。

表2 事故案例参数信息Table 2 Accident case parameter information

表3 真实与仿真结果对比Table 3 Comparison of actual and simulation results
对比表3中的结果发现,通过抛距公式得到的行人抛距值与真实抛距值、行人动力学响应的真实值与前挡风玻璃倾角-HIC拟合曲线得到的拟合公式值、行人动力学响应的真实值与前挡风玻璃倾角-胸腔连续3 ms最大加速度值拟合曲线得到的拟合公式值基本吻合,误差在5%以内,证明该方法的合理性以及准确性。
5 结论
1)分段计算公式不仅能反映抛距变化趋势,并在2个分段范围内均能较好地拟合实际抛距,平均误差为4.23%。
2)碰撞时车辆速度、行人走向对行人在路面上的位移影响较大。当碰撞车速大于35 km/h,即行人与车辆分离速度大于20 km/h时,此时行人与车辆分离时的速度与行人在路面上位移可以通过指数函数模型描述。
3)行人抛距随着车速的增大而增大,同一车速下,随着发动机罩倾斜程度增大,逐渐减小;头部HIC值随着行人走向的减少而减少,随着前挡风玻璃倾角的增大头部HIC值逐渐下降;随着行人走向的增大,胸部损伤风险明显下降,同一走向下,随着前挡风玻璃倾角的增大,胸部损伤风险增大。

