基于车桥耦合振动的高速铁路系杆拱桥吊杆优化布置*

张思远，喻 博

(1.中铁一局集团第五工程有限公司，陕西 宝鸡 721000； 2.深圳大学 土木与交通工程学院，广东 深圳 518000)

0 引言

系杆拱桥是1种兼具拱和梁优点的特殊桥型[1]，其充分发挥梁受弯、拱受压的结构特性，是1种具有较大探索研究性的大跨度桥梁形式[2-3]。

现代系杆拱桥的初期形式诞生于19世纪末的欧洲，采用刚性梁柔性拱结构，其特点是拱肋与吊杆之间铰接，拱肋只受轴向力，承受弯矩，这种结构又被称为兰格尔体系。此后，国外学者提出设想用斜吊杆代替竖吊杆，可以大幅提高结构刚度，此种结构被命名为尼尔森体系，美国、日本等国对该桥型进行一定的理论研究与设计实践，目前主要用于跨度及荷载较大的情况下。20世纪90年代我国学者先后提出异型系杆拱、网架系杆拱形式，其造型更美观、结构更轻盈，在满足实用性的前提下，更具美学欣赏价值[4-5]。

为满足列车行驶时的刚度要求，高速铁路线跨沟谷江河时，常采用钢管混凝土系杆拱桥结构。列车驶过桥梁时会引起桥梁结构振动，而这种振动与车体的振动、列车运行速度、吊杆布置形式、轨道平顺度等诸多因素相关[6]。目前，国内学者们对桥梁动力响应影响因素进行大量研究：曹雪琴等[7]研究列车过桥时简支梁桥的竖向振动及其影响因素；刘钊等[4-5]研究不同吊杆布置形式对桥梁结构静、动力特征的影响，同时提出不同桥型的构造设计要点；彭桂瀚等[8-9]以竖吊杆拱为基础设计斜吊杆拱桥并研究吊杆形式对结构稳定的影响；许士杰等[10]将车辆与桥梁看作1个相互作用的整体系统，研究车辆驶过系杆拱桥引起的动态响应。

从我国高速铁路系杆拱桥施工及设计领域的现状来看，吊杆的布局形式不断突破技术壁垒走向多样化，但施工设计多倾向于竖向双吊杆结构[11]，且对吊杆布置形式与车桥耦合振动影响因素研究较少，随着铁路桥型多元化的发展，特别是面临逐渐增加的桥梁跨度[12]，如何利用斜吊杆、网状吊杆拱桥结构上的优势和设计的合理性，以保证铁路桥梁的正常运营效力与行车安全性成为亟待解决的问题。据此，本文基于车桥耦合理论，分析在CRH2型动车组不同车速作用下、不同吊杆布置形式下对系杆拱桥跨中关键部位动力响应的影响，以期为未来系杆拱桥多元化设计提供理论依据。

1 工程概况及有限元模型

1.1 工程概况

以建成的某主跨度128 m系杆拱桥为工程背景进行研究，该桥为双线高速铁路钢管混凝土系杆拱桥，设计时速为250 km/h，最高限制350 km/h，采用有砟轨道，在设计布局上斜跨高速公路。全桥理论计算跨度为128 m，总长度为132.5 m，桥宽15.6 m，矢跨比1/5。理论拱轴线方程Y=0.8X-0.006 25X2，设计线型为二次抛物线。2片拱肋中心线为14.3 m，吊杆间距为14.4 m+16×6.2 m+14.4 m，每侧共设17对吊杆，拱肋设6道横撑，全桥立面图如图1所示。

图1 全桥立面Fig.1 Facade of whole bridge

1.2 有限元模型

1.2.1 钢管混凝土系杆拱桥空间模型

本文采用有限元分析软件ANSYS对桥梁进行三维空间建模。拱肋和横撑均为等截面beam188模拟，共188个单元，箱梁采用等截面实体单元模拟，共21 780个单元，吊杆采用link10单元模拟。全桥共60 114个节点，222 036个单元。不同吊杆形式有限元模型如图2所示。图2(a)为竖吊杆拱模型，图2(b)～(c)为以竖吊杆拱工程数据和ANSYS模型为基础设计的斜吊杆拱和网状吊杆拱模型，其吊杆布局均为等间距设置，斜吊杆拱上吊点水平投影位于相邻2根吊杆中线上，网状吊杆拱上吊点位于相邻吊杆正上方。为使模型更符合实际，以最大限度地减小未知因素对结果的干扰，在建模过程中吊杆交叉点处未作连接，并严格遵照原设计以控制未知变量出现[13]。

图2 不同吊杆形式有限元模型Fig.2 Finite element models of different suspender forms

1.2.2 车辆模型

为研究列车对拱桥的动力响应，车辆模型选取4动4拖的CRH2型高速动车组，模拟车辆过桥模型如图3所示。

图3 车辆过桥模型Fig.3 Model of train crossing bridge

2 吊杆布置对自振特性的影响分析

在桥梁动力响应方面，结构的初期振动频率和与之对应的振动形式对结构安全性和稳定性起到重要的控制作用，本文通过ANSYS空间模型，采用兰索斯法对空间结构进行模态分析[14]。将自振振型和频率以图表的形式表示出来。3种吊杆布局形式的自振频率和相应的振型见表1，不同吊杆布置结构的各向基频见表2。

由表1～2可知：1)主跨128 m系杆拱桥结构振型首先表现为拱肋对称横弯，拱肋横向基频为0.499 Hz左右；其首次竖向弯曲振型多表现为反对称竖弯，竖向基频在1.350～1.758 Hz之间；其扭转振型往往伴随着横向弯曲振动，扭转振型与横向弯曲振动是耦联的；2)主要的振动形式表现为拱肋的面外振动、桥梁整体竖向振动和扭转振动。吊杆布置形式对系杆拱的自振频率和相应模态形式效果显著，网状吊杆结构中拱梁发生第1阶竖向弯曲振动频率最高，为1.758 Hz，斜吊杆、网状吊杆竖向1阶自振频率增幅分别达17.38%，30.26%。同时斜吊杆、网状吊杆系梁横向基频均较竖吊杆降低3%左右。吊杆布置形式对拱肋的侧倾、系梁的横向弯曲及拱肋的侧向弯扭振动在初始频率数值上相近，其影响可忽略不计。

表1 3种吊杆形式下系杆拱桥的前5阶自振特性Table 1 First five order natural vibration characteristics of tied arch bridge under three suspender forms

表2 不同吊杆布置结构的各向基频Table 2 Fundamental frequency in each direction of different suspender layout structures Hz

3 钢管混凝土系杆拱桥振动响应分析

3.1 振动响应曲线

本文项目动车设计速度为250～350 km/h，在模拟过程中，CRH2型动车组因偏载产生的扭转作用忽略不计。动车以时速300 km/h通过桥梁时跨中横向和竖向位移、跨中横向和竖向加速度4个指标[15]的时程图如图4～7所示。参考《高速铁路设计规范》(TB 10621—2014)，在保证桥梁的各项动力响应参数均在规范允许限值内的同时，较全面直观地映射出桥梁动力性能，其中振动加速度和振动位移在桥梁整体振动分析中可作为重要评判依据[16]。

图4 跨中横向位移时程曲线Fig.4 Time history curve of transverse displacement in mid-span

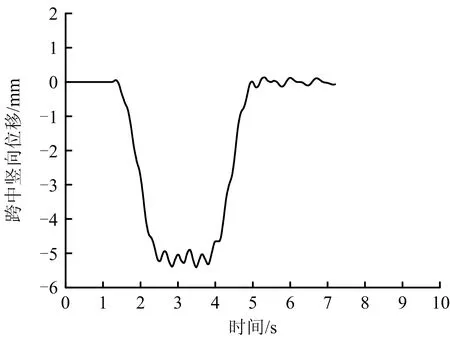
图5 跨中竖向位移时程曲线Fig.5 Time history curve of vertical displacement in mid-span

图6 跨中横向加速度时程曲线Fig.6 Time history curve of lateral acceleration in mid-span

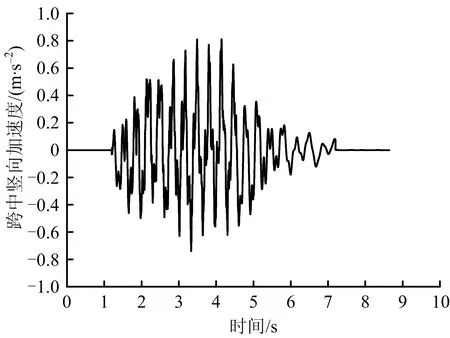
图7 跨中竖向加速度时程曲线Fig.7 Time history curve of vertical acceleration in mid-span

由图4～7可知，拱桥跨中横向位移最大值为0.964 mm，竖向位移峰值5.412 mm，跨中横向加速度最大值为0.774 m/s2，竖向加速度最大值为0.813 m/s2，且位移峰值、加速度峰值出现在车辆通过跨中结构的过程中，对照桥梁动力性能评定及标准均满足要求。

3.2 桥梁振动影响因素分析

3.2.1 速度影响

为研究速度对桥梁振动的影响，此处不考虑外力作用。阻尼比采用线性阻尼比，分别求得列车以设计允许速度过桥时拱桥跨中的竖向位移时程曲线及峰值对比如图8～9所示。拱桥跨中位移、加速度值见表3。

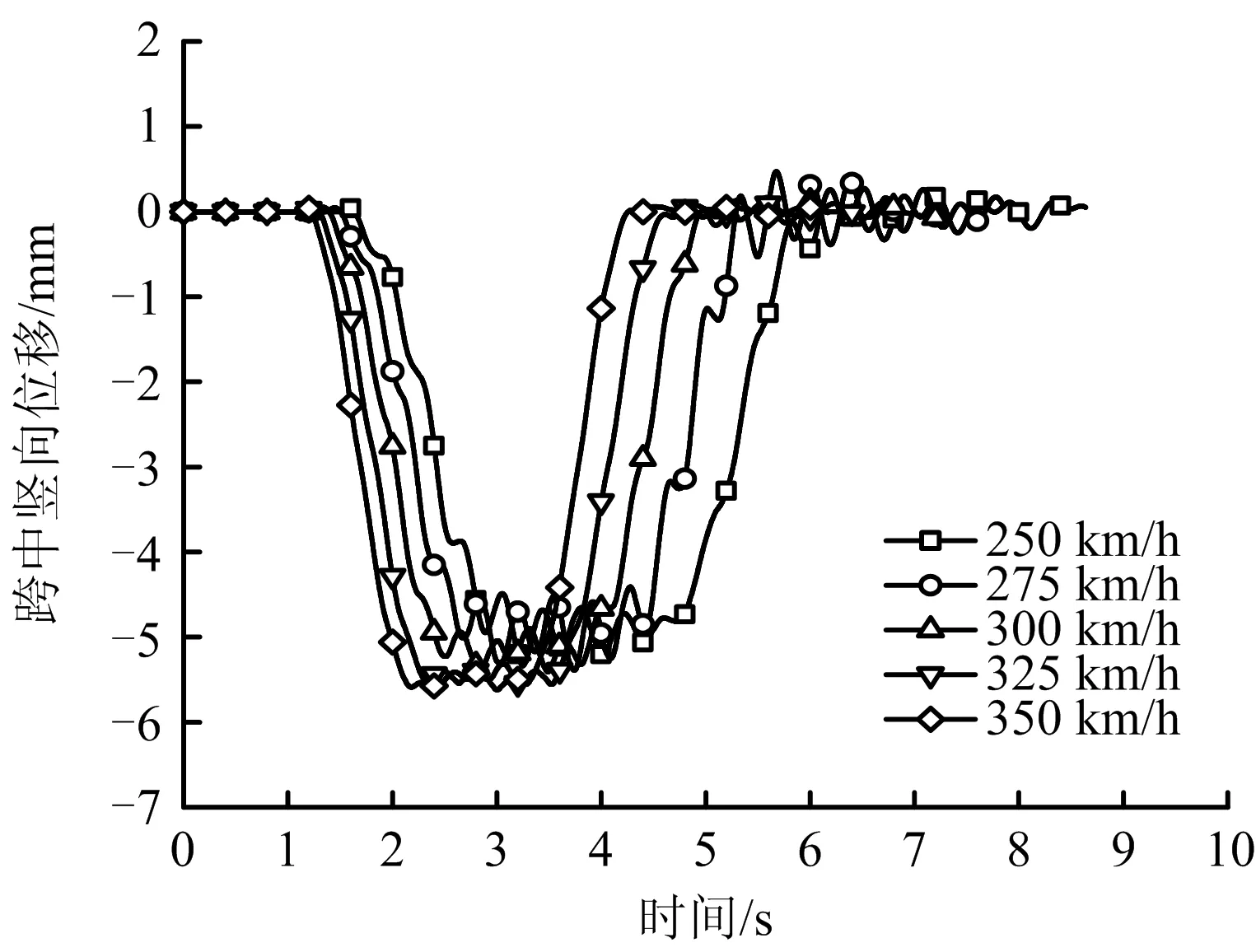
图8 不同车速跨中竖向位移曲线Fig.8 Curves of vertical displacement in mid-span under different train speeds

由图8～9及表3可知，列车以不同速度行驶经过桥面时，随着车速增加，跨中最大竖向位移值随之增大。拱桥跨中竖向位移峰值5.572 mm，小于限值85.33 mm(限值=L/1 500，桥长L=128 m)；横向位移峰值1.017 mm，小于限值32 mm(限值=L/ 4000)。竖向加速度最大值0.862 m/s2，小于0.35g(重力加速度g取10 m/s2，即3.5 m/s2)；横向加速度最大值0.830 m/s2，小于0.15g(即1.5 m/s2)。竖向位移增大约4.3%，加速度增大约34%，且桥梁的位移和加速度均未超过规范允许限值，桥梁振动情况良好。

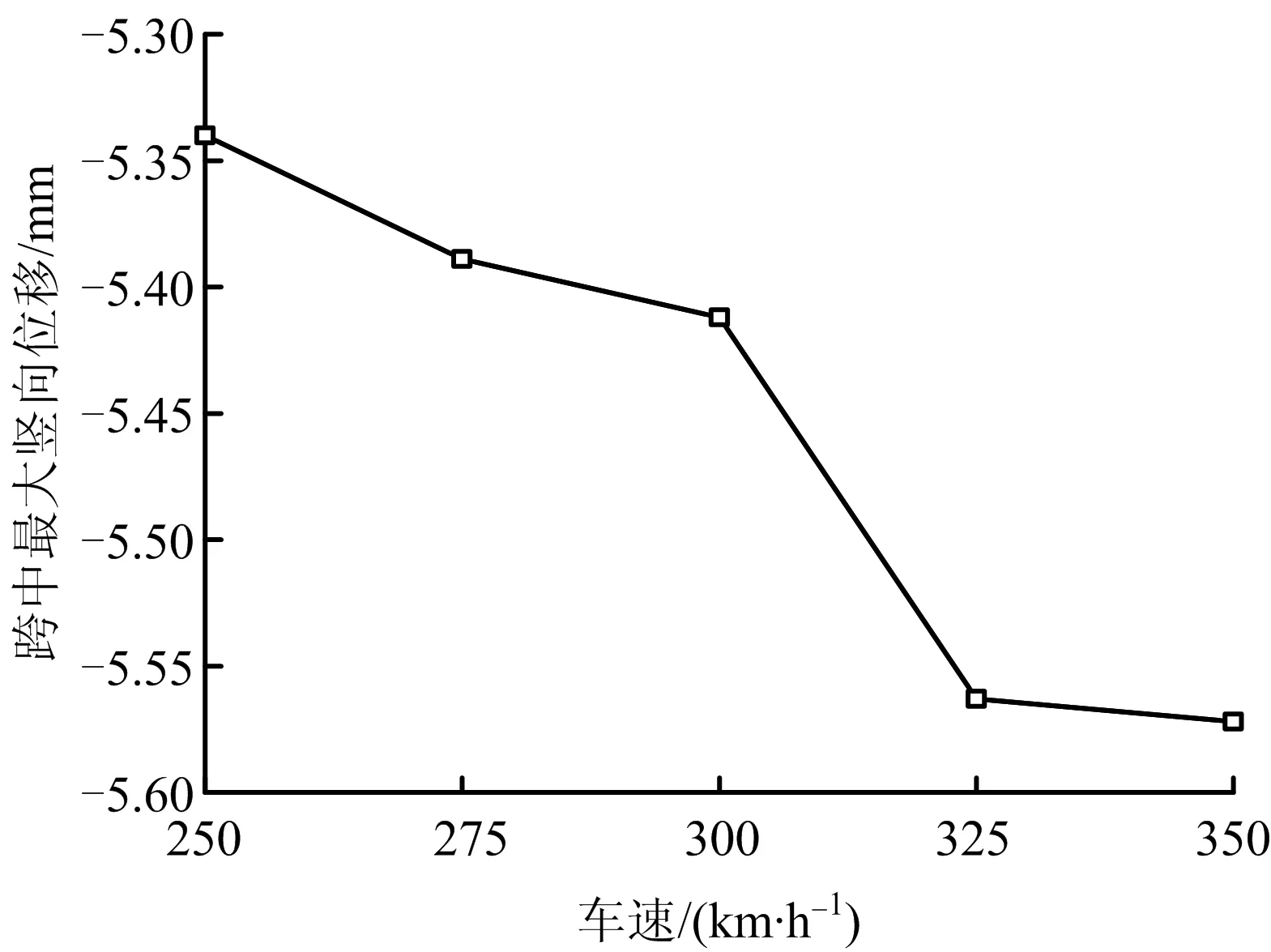
图9 跨中竖向位移峰值对比Fig.9 Comparison of peak vertical displacement in mid-span

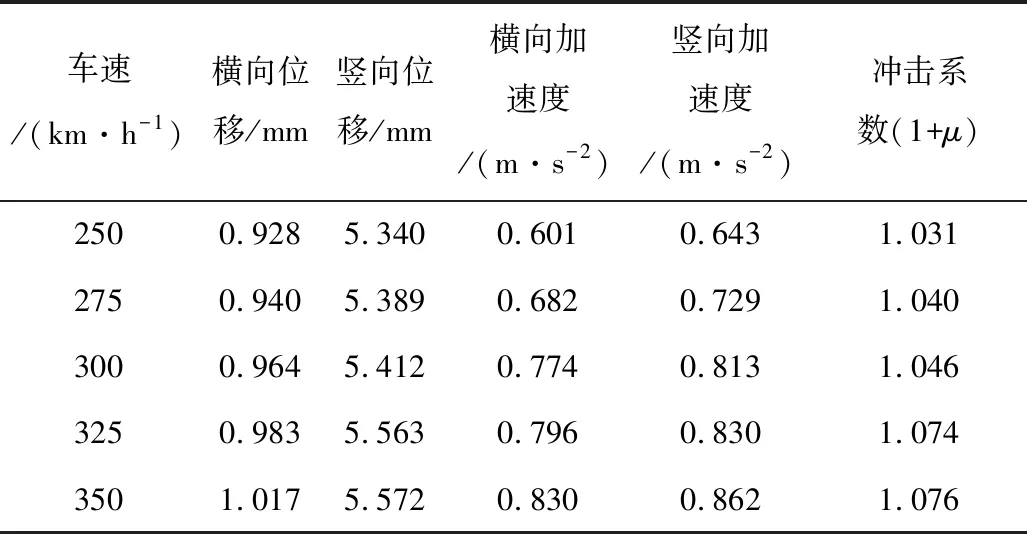
表3 不同速度条件下跨中最大位移和加速度Table 3 Maximum displacement and acceleration in mid-span under different speeds

由表3中最大动位移变化规律可知。随车辆运行速度的增加系杆拱桥冲击系数(1+μ)由1.031增至1.076，其变化趋势与简支梁桥相同。所以，合理地控制车辆行驶速度能够提高桥梁的安全性。

3.2.2 吊杆设计形式的影响

列车以设计允许速度通过斜吊杆拱、网状吊杆拱时，桥梁跨中横向、竖向位移，跨中竖向、横向加速度值见表4。不同吊杆布置形式下跨中横向、竖向位移、加速度对比如图10～13所示。

表4 斜吊杆和网状吊杆拱桥跨中最大位移和加速度Table 4 Maximum displacement and acceleration in mid-span of arch bridges with inclined suspenders and mesh suspenders

图10 跨中横向位移峰值Fig.10 Peak values of transverse displacement in mid-span

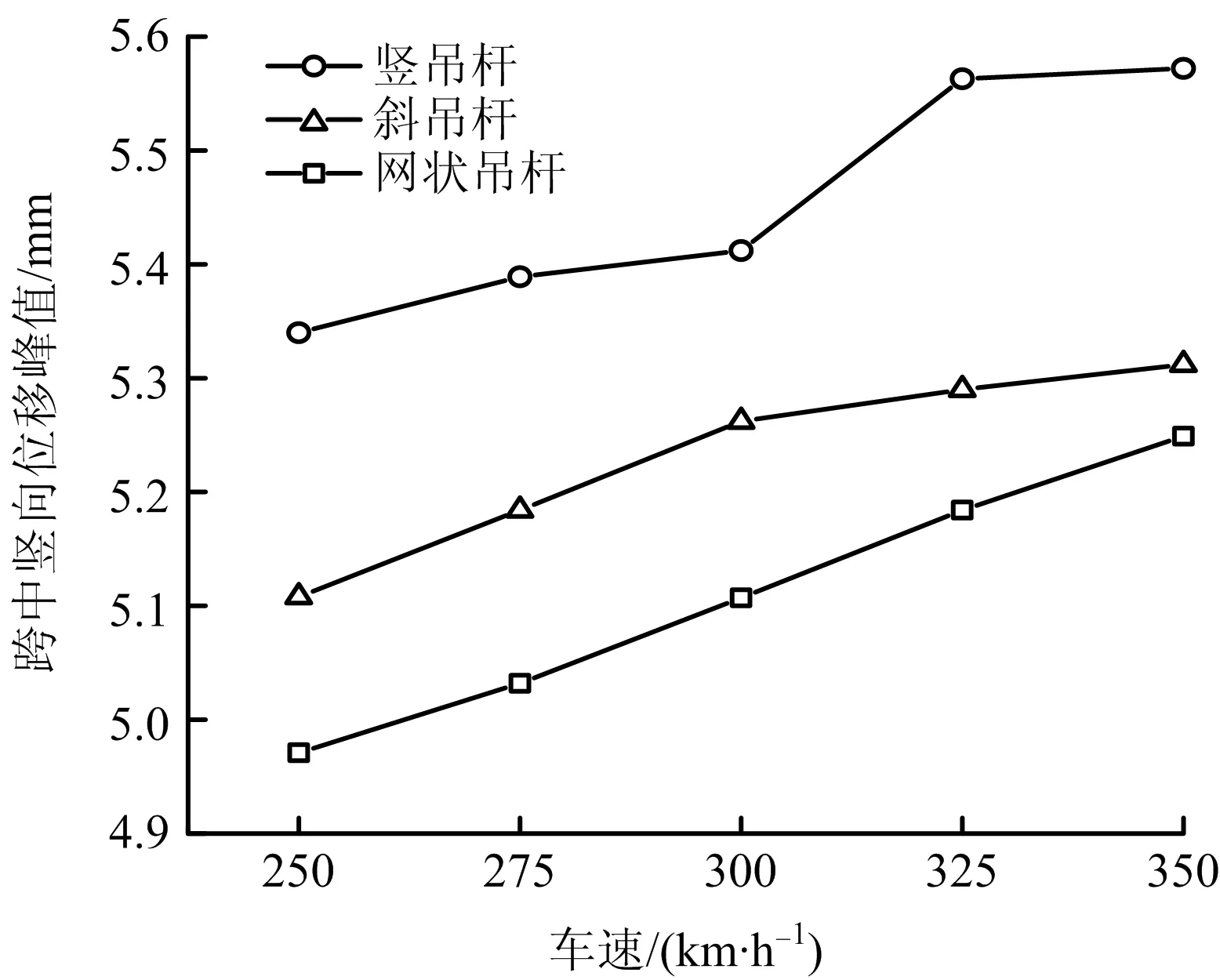
图11 跨中竖向位移峰值Fig.11 Peak values of vertical displacement in mid-span

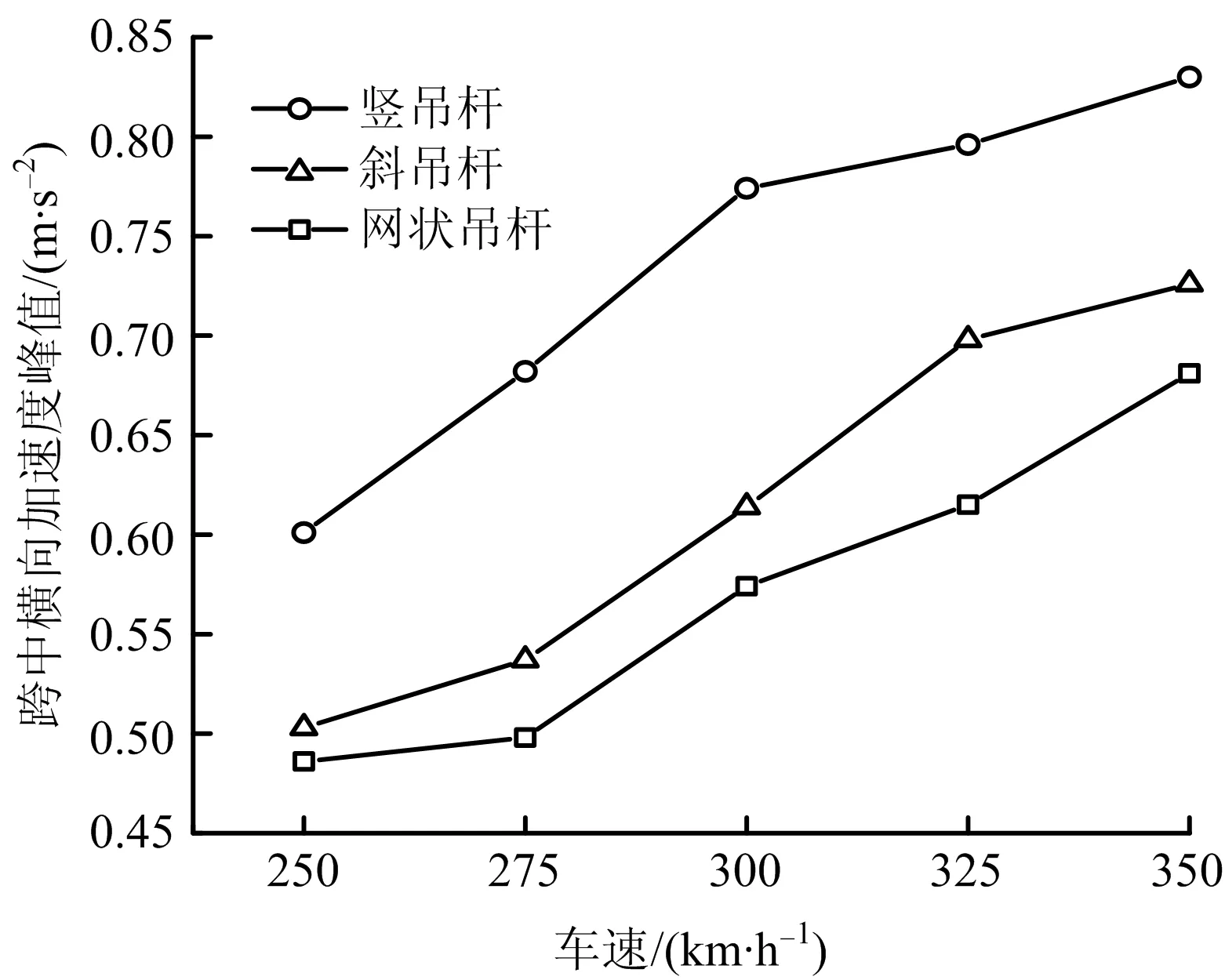
图12 跨中横向加速度峰值Fig.12 Peak values of lateral acceleration in mid-span

图13 跨中竖向加速度峰值Fig.13 Peak values of vertical acceleration in mid-span

由表3～4，图10～13分析结果可知，CRH2型动车组以300 km/h通过竖吊杆、斜吊杆和网状吊杆系杆拱桥时，桥梁跨中横向位移分别为0.964，0.962，0.959 mm，其变化微小，可以认为桥梁横向位移基本不变；跨中竖向位移幅值从小到大依次为网状吊杆(5.107 mm)<斜吊杆(5.262 mm)<竖吊杆(5.412 mm)，斜吊杆相对于竖吊杆降低0.150 mm，降幅达到2.8%，网状吊杆相对于竖吊杆降低0.305 mm，降幅达到5.6%；而3种结构中网状吊杆拱跨中横向、竖向加速度均最小，相对于竖吊杆分别降低25.84%和8.36%；斜吊杆、网状吊杆的车桥振动分析中桥梁各项参数动力响应均小于竖吊杆分析的各项参数动力响应，尤其是桥梁跨中竖向位移较之竖吊杆要明显降低，说明吊杆布置形式对桥梁的振动影响较大，可以有效地较低桥梁的位移和加速度。

4 结论

1)吊杆不同布置明显提高竖向1阶自振频率，斜吊杆、网状吊杆竖向1阶自振频率增幅分别达17.38%，30.26%。同时斜吊杆、网状吊杆系梁横向基频均较竖吊杆降低3%左右。但对系杆拱的横向自振频率影响不大。综合跨中挠度和竖向第1阶自振频率的比较可以发现，采用斜吊杆和网状吊杆对结构振频和模态有显著影响，对全桥的竖向刚度有较大的提高。

2)原桥在车速由250 km/h到350 km/h时，竖向挠度增大约4.3%，加速度增大约34%，且速度等级越高，愈发明显，因此合理地控制车辆行驶速度能够提高桥梁的安全性。

3)在斜吊杆、网状吊杆的车桥振动分析中，桥梁跨中竖向位移较之竖吊杆要明显降低，时速300 km/h时，斜吊杆降低0.150 mm，降幅达到2.8%；网状吊杆降低0.305 mm，降幅达到5.6%。结合其他动力参数说明网状吊杆具有最大的竖向刚度和最高的竖向振动基频，力学特性要优于竖吊杆。因此网状吊杆是最为合理的布置形式。未来在克服传统施工产生的技术复杂和设备落后的制约，大跨度系杆拱桥的设计和选型时应当充分考虑网状吊杆拱桥在力学性能上的优势。