地铁区间隧道竖井送风有效风量研究*
姜学鹏,杨 成,景 安,姜学坤
(1.武汉科技大学 资源与环境工程学院,湖北 武汉 430081; 2.武汉科技大学 消防安全技术研究所,湖北 武汉 430081; 3.青岛四方庞巴迪铁路运输设备有限公司,山东 青岛 266111)
0 引言
地铁工程构造特殊,区间隧道空间相对封闭,且人员密度高,逃生难度大,一旦发生火灾,将会造成严重的人员伤亡和重大财产损失,故合理的通风排烟设计参数是保障隧道内人员疏散环境安全的关键。当地铁区间隧道纵向通风排烟采用竖井送风时,若竖井两侧隧道边界条件相同,则两侧风流分配比例相同;当竖井两侧边界条件不同时,两侧风流分配比例则不同。实际作用于火灾事故区间的风量,即竖井送风有效风量是火灾烟气控制的关键。
部分学者对纵向通风排烟隧道采用竖井方式送风进行相关研究。谢宣等[1]通过数值模拟研究得到非火灾隧道段列车的阻塞作用,使中间竖井送风风流可流向火灾事故列车所在隧道段;陈外才[2]通过数值模拟研究热位差和轴流风机对隧道竖井送风的影响,并分析环境温度对隧道内空气温度、密度等的影响,提出公路隧道竖井集中送风通风方案;张铭鑫[3]通过模型试验研究公路隧道竖井送排式纵向通风中短道段气流状态,得出排风量与送风量的比例决定短道的流态形式等结论。上述研究多关注竖井送风问题,较少关注风量在竖井两侧隧道的分配问题,更未对竖井送风有效风量进行研究。因此,有必要研究竖井两侧边界条件不同时竖井送风有效风量,确定竖井送风有效风量的计算模型,可为地铁区间隧道纵向通风排烟设计提供技术支持。
综上所述,本文针对地铁区间隧道竖井送风有效风量,通过量纲分析推导地铁区间隧道竖井送风有效风量的无量纲公式,并采用数值模拟方法研究火源功率、火源位置、阻塞比、竖井送风风量等影响因素与有效风量之间的量化关系,进而确定无量纲竖井送风有效风量计算模型。
1 理论分析
影响竖井送风有效风量Qe的因素[4-11]包括火灾热释放率,火源距离,隧道阻塞比,竖井送风风量,空气密度,空气定压比热,空气温度,重力加速度,隧道水力直径。上述因素关系如式(1)所示:
f(W,L,β,Qs,ρ0,cp,T0,g,HD)=Qe
(1)
式中:W为热释放速率,kW;L为火源距离,m;β为隧道阻塞比;Qs为竖井送风风量,m3/s;ρ0为空气密度,kg/m3,1.2 kg/m3;cp为空气的定压热容,一般为1.02 kJ/(kg·K);T0为环境温度,K,取T0=293 K;g为重力加速度,取g=9.81 m/s2;HD为隧道水力直径,m。
设质量[M],时间[t],长度[L],温度[T]为4个基本量纲,上述9个物理量均可由4个基本量纲表示,式(1)所对应的量纲公式为式(2):
f(ML2t-3,L,1,L3t-1,ML-3,L2t-2T-1,T,Lt-2,L)=L3t-1
(2)
选取HD,g,ρ0,T0为基本物理量,根据π定理,式(2)可变成式(3):
f(π1,π2,π3,π4,π5,π6)=0
(3)
其中π1~π6的量纲方程如式(4)所示:
(4)
式中:指数α1~α6,β1~β6,γ1~γ6,ε1~ε6分别为π1~π6的量纲。
通过量纲方程求解可得6个无量纲项,如式(5)所示:
(5)
根据式(3)可得式(6):
(6)
根据相似理论的规则,式(6)可变为式(7):
(7)
因此得式(8):
(8)
式(8)可化为式(9):
Qe*=f(W*,L*,β,Qs*)
(9)
式中:W*,L*,Qs*分别为无量纲火源功率、无量纲火源距离和无量纲竖井送风量。
其中W*,L*,Qs*计算如式(10)所示:
(10)
将式(10)写成函数形式得式(11):
Qe*=k1(W*)k2(L*)k3(β)k4(Qs*)k5
(11)
式中:k2~k5分别是无量纲有效风量Qe*与W*,L*,β,Qs*的比例系数;k1是由比例系数k2,k3,k4,k5唯一确定的常数。
式(9)和式(11)表明无量纲竖井送风有效风量Qe*取决于无量纲火源功率W*、无量纲火源距离L*、阻塞比β和无量纲竖井送风量Qs*。因此只需通过数值模拟和数据拟合确定Qe*与W*,L*,β*,Qs*的函数关系,得到k1~k5,即可得到竖井送风有效风量的无量纲计算模型。
2 数值模拟
2.1 模型建立与火灾场景设置
1)数值建模
利用FDS6.7.1建立水下盾构隧道(长2 600 m×宽12 m×高15.2 m)地铁区间隧道全尺寸模型,列车行车区间长4 200 m×宽4.8 m×高4.4 m(2站3区间),其中火灾区间长2 600 m,区间隧道示意图及盾构横断面布置如图1所示。有效站台左侧设置顶部风机竖井,面积为6 m(长)×3.2 m(宽),两竖井间距为2 710 m。区间隧道壁面设为“CONCRETE”混凝土表面,列车车体为“STEEL”钢结构材质。区间两端均设为与外界相通的开口边界“OPEN”。隧道内空气及各固体表面的初始温度为20 ℃,大气压为101.325 kPa的标准大气压。
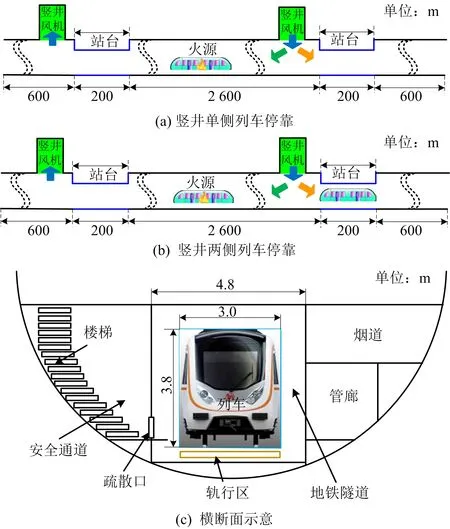
图1 竖井送风示意及横断面示意Fig.1 Schematic diagrams of shaft air supply and cross section
2)火灾场景设置
地铁列车火灾热释放速率取5,6,7.5,9,10 MW[12-13],火源设置于列车外底部中间位置[14],火源尺寸为6 m(长)×2 m(宽),为快速增长火(火灾增长速率0.046 89 kW/s2)。火灾发生后,区间上游竖井风机送风、下游竖井风机排烟。火灾模拟运行时间为900 s,当燃烧进行至800 s时,隧道内的风速等参数均达到稳定状态,选取800~900 s的模拟数据平均值进行研讨。
区间隧道列车阻塞比(列车与区间隧道截面积之比)约为50%,基于此工程,采用数值模拟方法,设计4组共40个工况,研究竖井送风有效风量与火灾热释放速率、火源距离、阻塞比及竖井送风风量之间的量化关系。具体工况见表1。
2.2 网格独立性分析
FDS建模中,网格尺寸是影响结果的关键因素。网格尺寸为1/16D*~1/4D*[8,14],模拟结果与实验结果非常吻合,D*计算如式(12)所示:
(12)
式中:D*为火源特征直径,m。
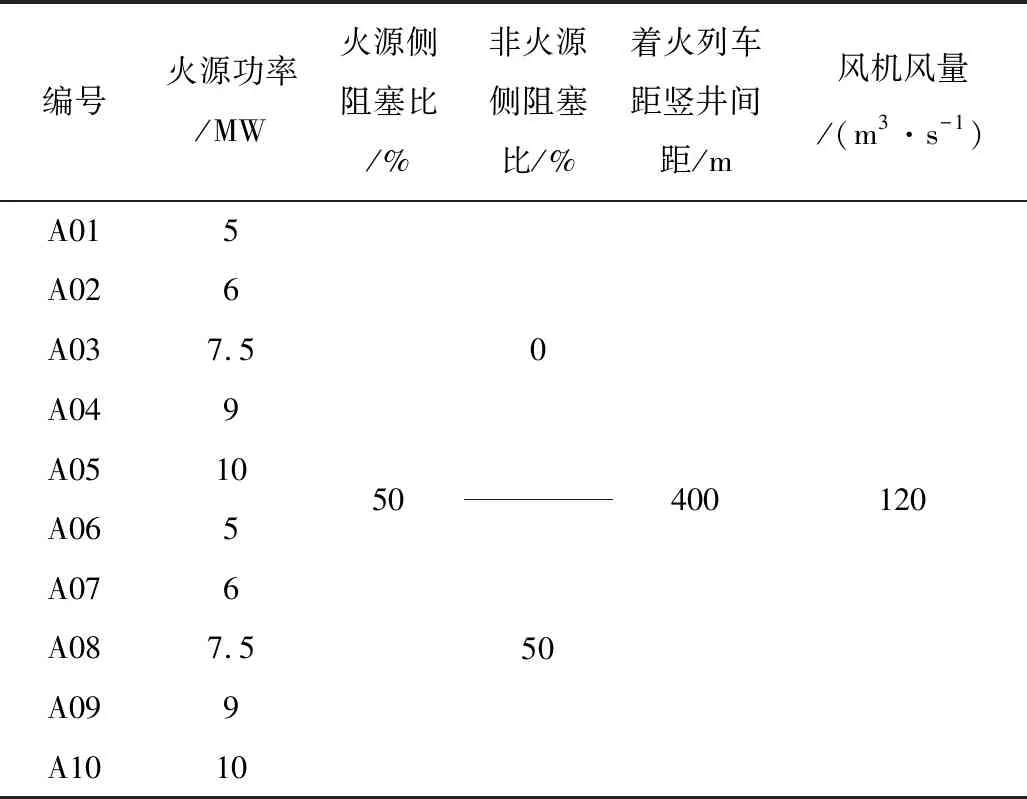
表1 竖井送风有效风量研究工况Table 1 Research conditions for effective air volume of shaft air supply

表1(续)
将W=5 MW带入式(12),得出网格尺寸为0.1~0.4 m较合适,考虑到火源附近相关热力学参数变化较大,近火源区域(±20 m范围)网格尺寸更密,能够使模拟结果更加精确,网格划分见表2。
对表2中5种网格尺寸进行尝试性计算,结果表明:网格尺寸Ⅱ与网格尺寸Ⅰ计算结果一致,且模拟所需时间较网格尺寸Ⅰ更短。考虑模拟时间长短及模拟结果准确性,可知网格尺寸Ⅱ为最佳网格尺寸,即近火源区域网格尺寸设为0.1 m×0.1 m×0.1 m,火源远端网格尺寸设为0.4 m×0.4 m×0.4 m。
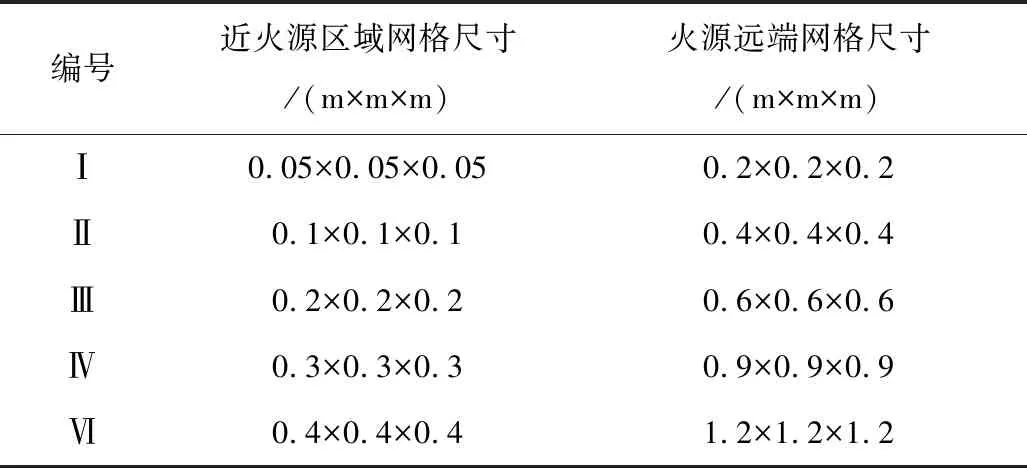
表2 网格尺寸划分Table 2 Grid size division
3 模拟结果与分析
3.1 火源功率影响
列车发生火灾停靠于距送风竖井400 m位置、竖井送风风量120 m3/s时,不同火源功率下竖井送风有效风量数值模拟结果如图2所示。由图2可知,无量纲竖井送风有效风量Qe*基本不随无量纲火源功率W*的增大而改变。随着火源功率的增大,抑制火灾烟气逆流所需的纵向临界风速逐渐增大,临界风速抑制火灾烟气及火风压,无法对竖井送风风流分配产生较大影响。
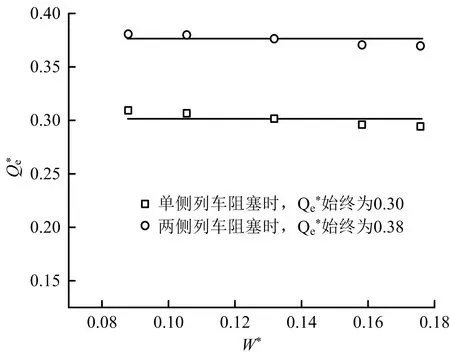
图2 无量纲竖井有效风量Qe*随无量纲火源功率W* 变化曲线Fig.2 Variation curve of effective air volume Qe* of dimensionless shaft with dimensionless fire power W*
3.2 火源距离影响
在火灾热释放速率为7.5 MW,竖井送风风量120 m3/s情况下,火源距送风竖井不同距离时竖井送风有效风量数值模拟结果如图3所示。由图3可知,无论竖井单侧列车停靠或两侧列车停靠,无量纲竖井送风有效风量均不随无量纲火源距离的改变而改变,即竖井送风有效风量与火源距离之间不存在函数关系。
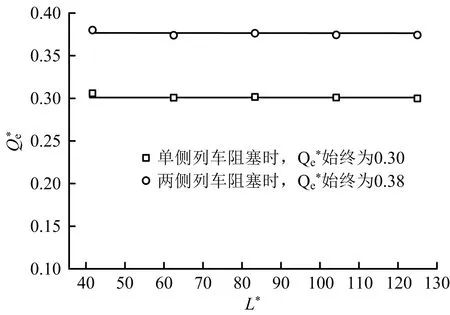
图3 无量纲竖井有效风量Qe*随无量纲火源距离L* 变化曲线Fig.3 Variation curve of effective air volume Qe* of dimensionless shaft with dimensionless fire source distance L*
3.3 阻塞比影响
在火灾热释放速率为7.5 MW、火灾列车距送风竖井400 m、竖井送风风量120 m3/s情况下,不同阻塞比时竖井送风有效风量数值模拟结果如图4所示。由图4可知,竖井单侧列车停靠时,无量纲竖井送风有效风量Qe*与阻塞比β关系曲线呈-1.08次方曲线;两侧列车停靠时,无量纲竖井送风有效风量Qe*与阻塞比β关系曲线呈-0.22次方曲线。2条曲线的相关系数均为0.98,拟合曲线函数可靠性较高。
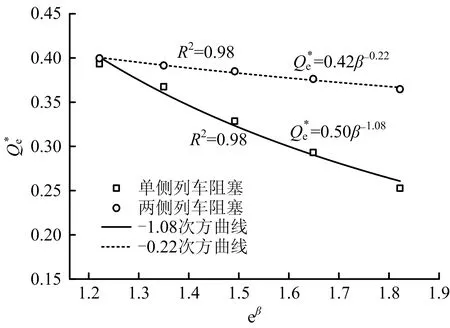
图4 无量纲竖井有效风量Qe*随阻塞比β变化曲线Fig.4 Variation curve of effective air volume Qe* of dimensionless shaft with drag plug ratio β
区间隧道列车阻塞作用影响竖井送风有效风量,随着阻塞比的增大,竖井送风有效风量逐渐减小。当竖井两侧列车阻塞时,因竖井两侧阻塞比相同,阻塞比对竖井送风有效风量的影响较小;当单侧列车停靠时,阻塞作用导致竖井送风风量向无列车阻塞区间分流更多,因此单侧列车停靠时竖井送风有效风量相较于两侧列车阻塞时,有效风量的减小比例更大。
3.4 竖井送风风量影响
在火灾热释放速率为7.5 MW,火灾列车距送风竖井400 m情况下,竖井不同送风风量与竖井送风有效风量数值模拟结果如图5所示。由图5可知,竖井单侧列车停靠时,无量纲竖井送风有效风量与无量纲竖井送风量关系曲线呈1.11次方曲线;两侧列车停靠时,无量纲竖井送风有效风量与无量纲竖井送风风量关系曲线呈1.07次方曲线。2条曲线的相关系数均为0.99,拟合曲线函数可靠性较高。随着竖井送风风量的增大,有效风量逐渐增大,且有效风量增大趋势高于送风风量。
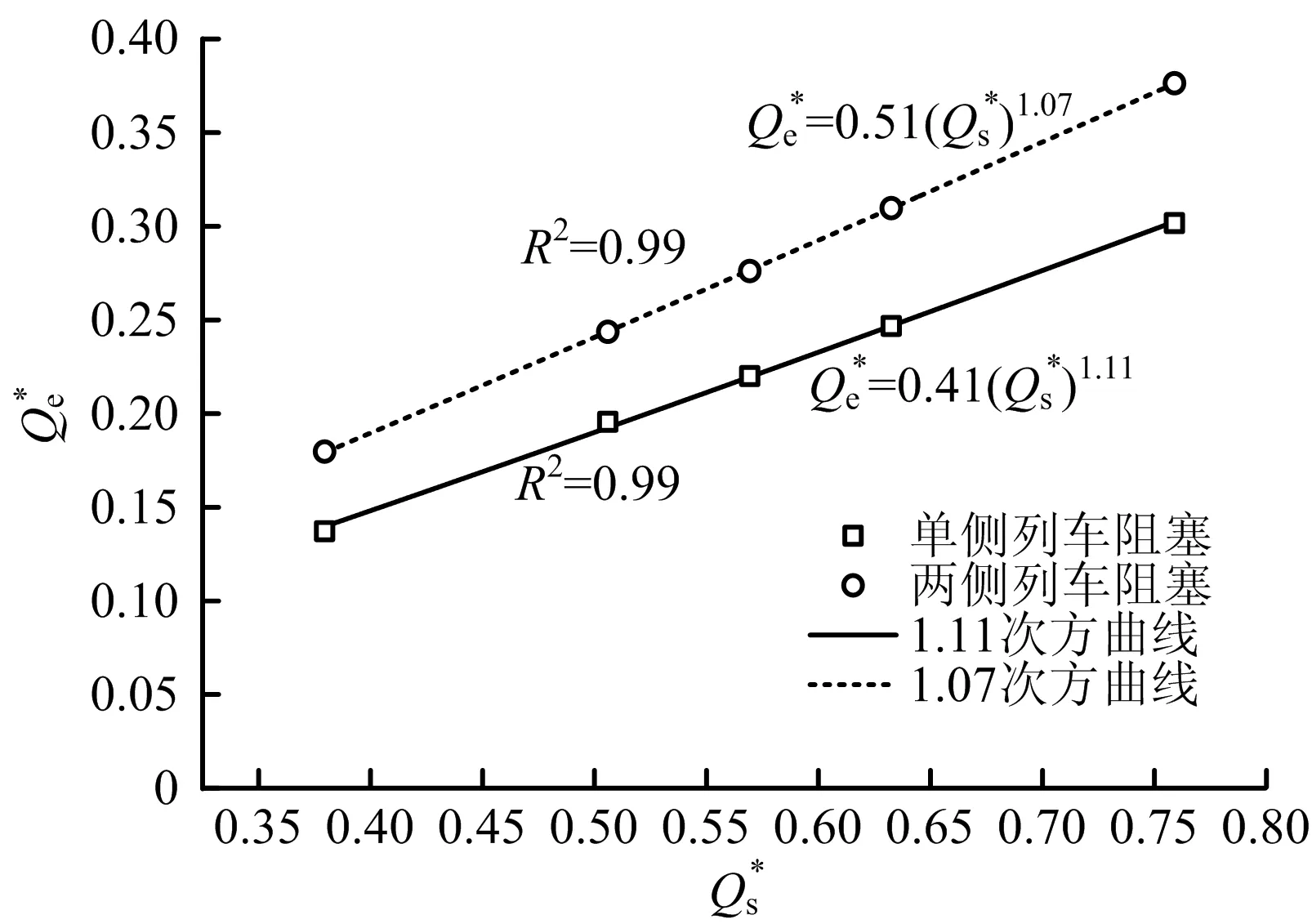
图5 无量纲竖井有效风量Qe*随无量纲竖井送风量Qs* 变化曲线Fig.5 Change curve of effective air volume Qe* of dimensionless shaft with dimensionless shaft air supply Qs*
3.5 竖井送风有效风量计算模型确定
根据上述分析可得竖井送风有效风量Qe*与β,Qs*的函数关系,结合式(9),式(10)可得式(13):
(13)
为确定式(13)中系数k1,k1′的值,将所得的Qe*,β-1.08Qs*1.11,β-0.22Qs*1.07的计算值绘制于图6。由图6可知,竖井送风有效风量模拟结果在1条直线附近波动,k1为1.45,相关系数为0.99;k1′为1.81,相关系数为0.99,表明无量纲竖井送风有效风量计算模型和数值模拟结果的一致性。将k1=1.45、k1′=1.81带入式(13)可得无量纲竖井送风有效风量的计算模型,如式(14)所示:
(14)
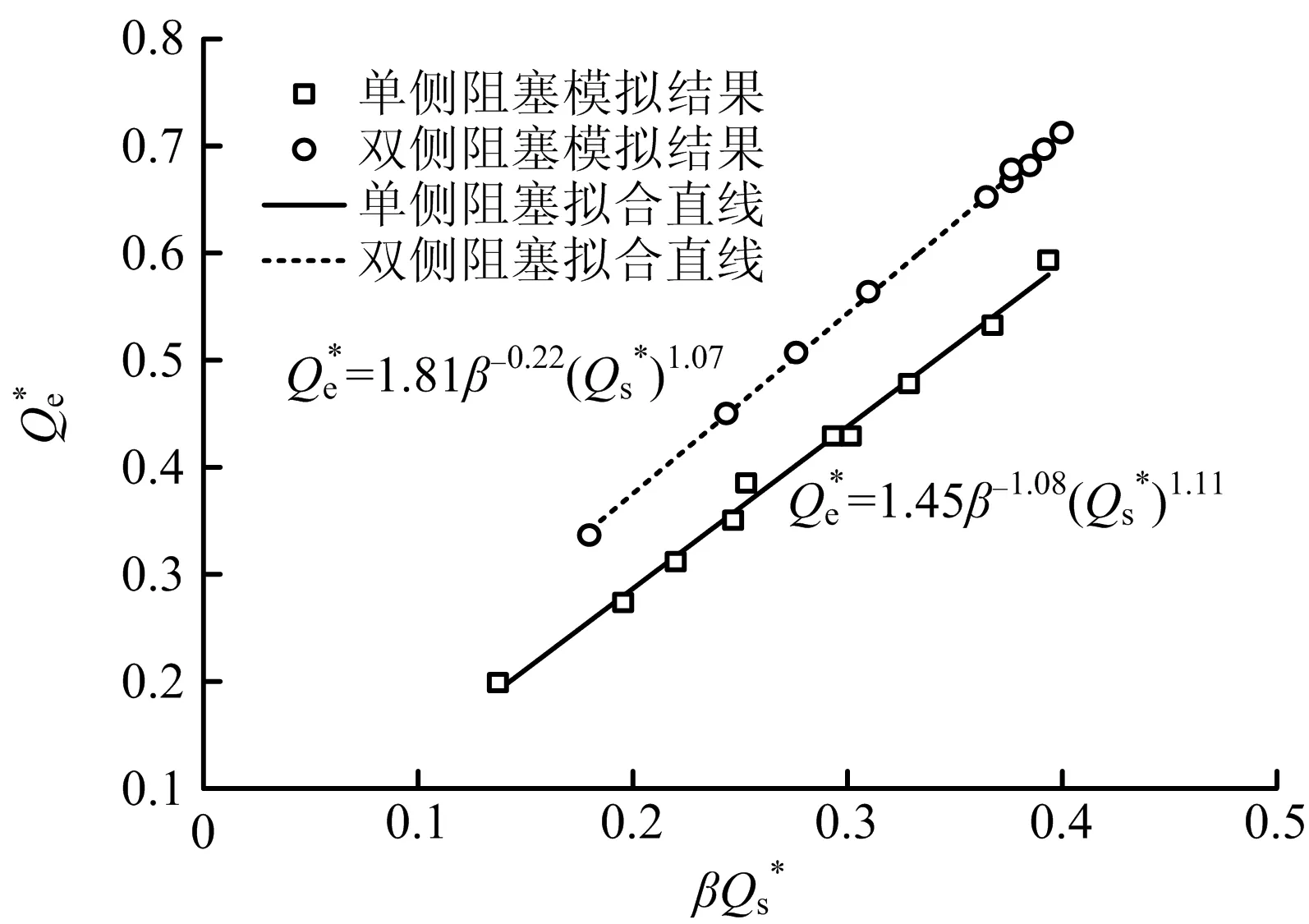
图6 无量纲竖井有效风量Qe*随β·Qs*变化曲线Fig.6 Change curve of effective air volume Qe* of dimensionless shaft with β·Qs
4 结论
1)根据量纲分析π定理,推导出地铁区间隧道竖井送风有效风量的无量纲公式;进而通过对数值模拟结果的拟合,明确无量纲竖井送风有效风量与无量纲火源功率、无量纲火源距离、阻塞比和无量纲竖井送风量之间的参数关系,得到竖井送风有效风量的无量纲计算模型。
2)竖井送风进行纵向排烟的地铁区间隧道,阻塞比对竖井送风有效风量影响显著,随着阻塞比的增大,有效风量逐渐减小。单侧列车停靠时,无量纲有效风量Qe*与阻塞比β呈-1.08次方减小关系;两侧列车停靠时,无量纲有效风量Qe*与阻塞比β呈-0.22次方减小关系。
3)单侧列车停靠时,无量纲有效风量与无量纲送风风量呈1.11次方增大关系;两侧列车停靠时,无量纲有效风量与无量纲送风风量呈1.07次方增大关系。随着竖井送风风量的增大,有效风量逐渐增大,且有效风量增大比例高于送风风量。

