GAPSO-KELM在滚动轴承故障诊断中的应用

方俊豪，陈正坤，陈保家，陈学力

GAPSO-KELM在滚动轴承故障诊断中的应用

方俊豪，陈正坤，陈保家*，陈学力

（三峡大学 机械与动力学院，湖北 宜昌 443002）

为了减小故障特征提取对信号处理方法和人工经验的依赖性、降低诊断模型的计算复杂度、有效提高诊断精度，本文提出了一种卷积神经网络（CNN）与核极限学习机（KELM）相结合的滚动轴承故障诊断方法。首先，直接将不同故障模式下的滚动轴承原始振动信号进行分段处理，用以构建训练集、验证集和测试集。其次，利用CNN卷积运算提取特征，通过池化运算提炼简化特征。最后，将提取后的特征用来训练KELM，并采用遗传粒子群（GAPSO）算法对KELM的惩罚系数与核参数进行优化设置，得到故障诊断模型。为评估方法有效性，采用同工况和变工况条件下进行实验测试，并与CNN-SVM、经典AlexNet 、VGG方法进行比较，结果显示该方法具有更好的准确性和稳定性。

卷积神经网络；滚动轴承；核极限学习机；故障诊断

滚动轴承是旋转机械中的重要部件，其健康状态对整个设备的安全平稳运行具有重大的影响[1]。滚动轴承故障诊断问题一直是学者研究的热点，主要集中在故障特征的有效提取与故障模式的准确识别这两方面。

传统的故障特征提取方法是利用时域、频域或时频域信号处理方法提取反映轴承故障信息的时频域特征。陈保家等[2]针对齿轮故障振动信号多分量频带重叠引发的故障模式混淆问题，提出一种基于最大重叠离散小波包变换（Maximal Overlap Discrete Wavelet Packet Transform，MODWPT）边际谱特征和粒子群优化－支持向量机（Particle Swarm Optimization- Support Vector Machine，PSO-SVM）的故障诊断方法。李伟[3]提出一种基于集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）和Teager能量算子的故障特征提取方法，利用EEMD分解样本信号得到若干本证模量函数（Intrinsic Mode Function，IMF）的Teager能量算子，取重构信号模糊熵及其对应概率密度函数的波形指标，作为基本特征参数进行故障诊断。但传统的故障特征提取方法严重依赖于信号处理方法本身的有效性和特征提取的科学性。

深度学习是机器学习领域中一个新的研究方向，通过构建多个非线性隐藏层，实现对特征信息的逐层提取。深度神经网络很好地解决了特征自适应学习和提取问题，并且其非线性表达能力强，诊断性能好[4]。在机械故障诊断领域，深度学习得到了学者的重视与研究，张绍辉[5]采用稀疏自编码与平方预测误差结合方法，对轴承故障区域进行了准确的定位。曲建岭等[6]提出了基于一维CNN（Convolutional Neural Networks，卷积神经网络）的层级化轴承故障诊断方法，结果显示该方法具有良好的故障分类性能和泛化特性。研究表明，卷积神经网络通过逐层交替的卷积层和池化层提取特征，在特征提取方面展现出了优良的特性。

常用的故障模式识别方法有聚类分析、人工神经网络、支持向量机（SVM）等，这些方法在实际的诊断应用当中还存在一些问题和限制。聚类分析在处理大规模高维数据时效果较差；SVM的计算复杂度较高，易产生过拟合现象；人工神经网络的准确性严重依赖于大样本数据，其训练速度较慢。

极限学习机（Extreme Learning Machine，ELM）是Huang等[7]提出的一种单隐层前馈神经网络，可以随机产生输入层与隐含层的连接权值以及隐含层神经元的阈值，其算法具有学习速率快、泛化性能强等优点，近年来得到了广泛的关注与应用[8]。但是ELM是浅层网络，若模型的输入特征不足，将会对结果产生较大的影响。

核极限学习机（Kernel Extreme Learning Machine，KELM）将核函数带进极限学习机中，该决策模型比常规ELM模型鲁棒性更强、泛化性能更好。宋佳等[9]采用KELM结合生物地理学优化（Biogeography-Based Optimization，BBO）算法开展了飞行器故障诊断方法研究。崔鹏宇等[10]提出了一种基于多尺度排列熵（Multiscale Permutation Entropy，MPE）和非线性加权组合的双核极限学习机（DK-ELM）的滚动轴承故障诊断方法。但KELM核参数和惩罚参数的设定一般随经验而定，设置不当会直接影响学习机的诊断效果。所以采用有效的参数优化选择方法在KELM中对关键参数进行精准设置显得尤为重要。

结合CNN和KELM各自优点，本文提出一种基于CNN与KELM的滚动轴承故障诊断方法，首先以一维振动信号作为模型输入，其次使用一维卷积神经网络进行故障特征提取，再输入到核极限学习机中实现故障分类。实验数据表明，在不同工况下该方法体现出极高的故障诊断准确率与较强的鲁棒性。

1 理论基础

1.1 卷积神经网络

CNN卷积层将输入信号局部区域与滤波器内核进行卷积操作，在激活函数的作用下生成输出特征。每个滤波器使用相同的内核提取输入信号局部特征。一个滤波器对应下一层中的一帧，帧的数量称为该层的深度。此外，第一层的小内核很容易受到工业环境中常见的高频噪声的干扰。因此，为了捕获中低频频段振动信号的有用信息，参考第一层宽卷积核深度神经网络（Deep Convolutional Neural Networks with First-Layer Kernel，WDCNN）模型参数[11]，卷积层采用宽卷积核，卷积过程描述为：

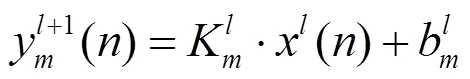
卷积之后，通过激活函数以获得非线性特征，增强模型的特征表达能力。ReLU（Rectified Linear Unit）作为激活函数用以加速CNN的收敛过程。ReLU的表达式为：

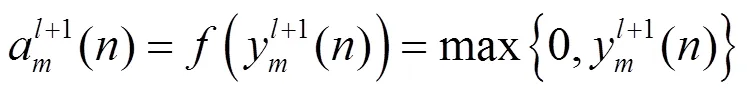
卷积之后添加池化层是很常见的。它用作下采样操作，可减少特征的空间大小和网络参数。最常用的池化层是最大池化层，它对输入要素执行局部最大运算，以减少参数并获得位置不变的要素。最大池转换的描述为：

1.2 核极限学习机

极限学习机是一种单隐层前馈神经网络（Single Hidden Layer Feedforward Neural Network，SLFN）的训练算法，SLFN模型可表示为：

式中：为输入数据；为连接隐藏层与输出层的权值向量；为隐藏层输出矩阵。

在ELM算法中有：

式中：为输入样本的类标志向量组成的矩阵；为惩罚系数；为单位矩阵。

核极限学习机借鉴了支持向量机（SVM）的思想[12]，采用核函数代替ELM隐层节点的特征映射。对于KELM，输出向量为：

核函数表示为：

一般选择径向基函数（RBF，Radial Basis Functions）作为KELM[13]的核函数：

所以KELM的输出方程为：

式中：为输入向量的维数。

1.3 遗传粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）最初是由Kenedy和Eberhart[15]基于粒子或鸟类的自然行为开发的，它是针对多维非线性复杂问题的非常有效的基于种群的优化程序。根据Kennedy等的观点，对于每个粒子，其位置均用以下方式更新：

本文利用粒子群优化算法和遗传算法（Genetic Algorithm，GA）[16]，结合两者的优点，既有GA算法的强大全局寻优能力，又有PSO算法的迅速收敛能力，形成遗传粒子群算法（GA-PSO）优化核极限学习机的核参数和惩罚系数，核参数和惩罚系数对KELM算法性能会有影响[17]，影响核函数的作用范围，影响模型的稳定性。以粒子群算法为主体，引入遗传算法中改进后的选择、交叉及变异算法，构建改进遗传粒子群GA-PSO的混合算法，来优化粒子群的局部与整体寻优能力。提出以GA-PSO算法混合优化核极限学习机，其算法流程如图1所示。

图1 GA-PSO算法流程图

2 方法流程

诊断模型如图2所示，主要由信号输入层、卷积层池化层、全连接层和核极限学习机组成。其中，1-D CNN模型由2个卷积层、2个池化层和1个全连接层组成。第1层卷积层核大小64，核数量1，步长1。第2个卷积层核大小3，核数量1，步长1。两个池化窗口尺寸和步长为2，其中(, x)代表了核函数。全连接层后采用KELM进行分类识别。步骤如下：

（1）获取轴承的振动信号，并对样本进行划分；

（2）划分数据集，贴标签，并对卷积神经网络参数设置初始化；

（3）训练集训练网络，模型提取故障特征；

（4）将特征输入KELM模型中；

（5）采用GA-PSO算法优化模型参数，得到最优诊断模型。

图2 模型结构图

3 实验与分析

3.1 实验说明

实验计算采用Google公司的Tensorflow框架，使用Anaconda软件编程，计算机配置处理器为Inter(R) Xeon(R) Gold 5120 CPU@2.20 GHz 2.20 GHz（2处理器）,16 GB运行内存。

为了验证提出方法在实际滚动轴承故障诊断中的有效性，本文使用美国Spectra Quest公司设计的机械故障综合模拟实验台，如图3所示，主要由驱动电机、转速表、转子基座、载荷和试验轴承等组成。传感器采用PCB352C33单轴振动加速度传感器，分别安装在试验轴承的水平方向和垂直方向进行同步数据采集。试验轴承型号为ER12KCL，包括正常、滚动体故障、内圈故障和外圈故障和共四种轴承状态类型，其中滚动体故障在轴承内部，故障点不可见，具体如图4所示。试验轴承运行转速为1600 r/min，采样频率20480 Hz，分别采集不同故障类型轴承运行状态下的振动加速度数据。

3.2 数据说明

将各运行状态采集到的实验数据做归一化处理并分段，每段样本振动信号包含1024个数据点，轴承每类运行状态包含1000个样本，数据集总共4000个样本，轴承运行的时域波形图如图5所示。使用one-hot编码技术对样本数据做标签，同样本下随机分配划分训练集、验证集和测试集组成数据集，如表1所示。

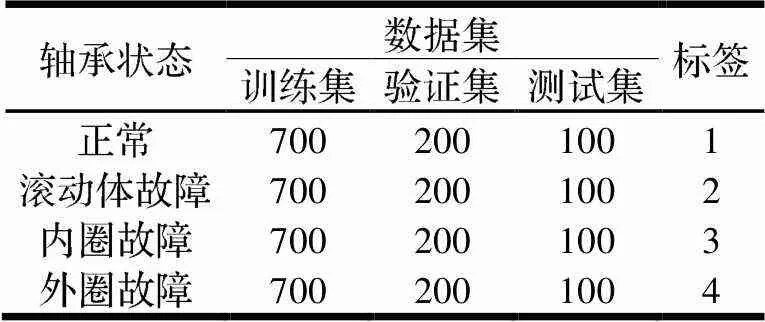
表1 四种轴承状态数据集

图3 机械故障综合模拟实验台（重载）

图4 四种不同类型的轴承

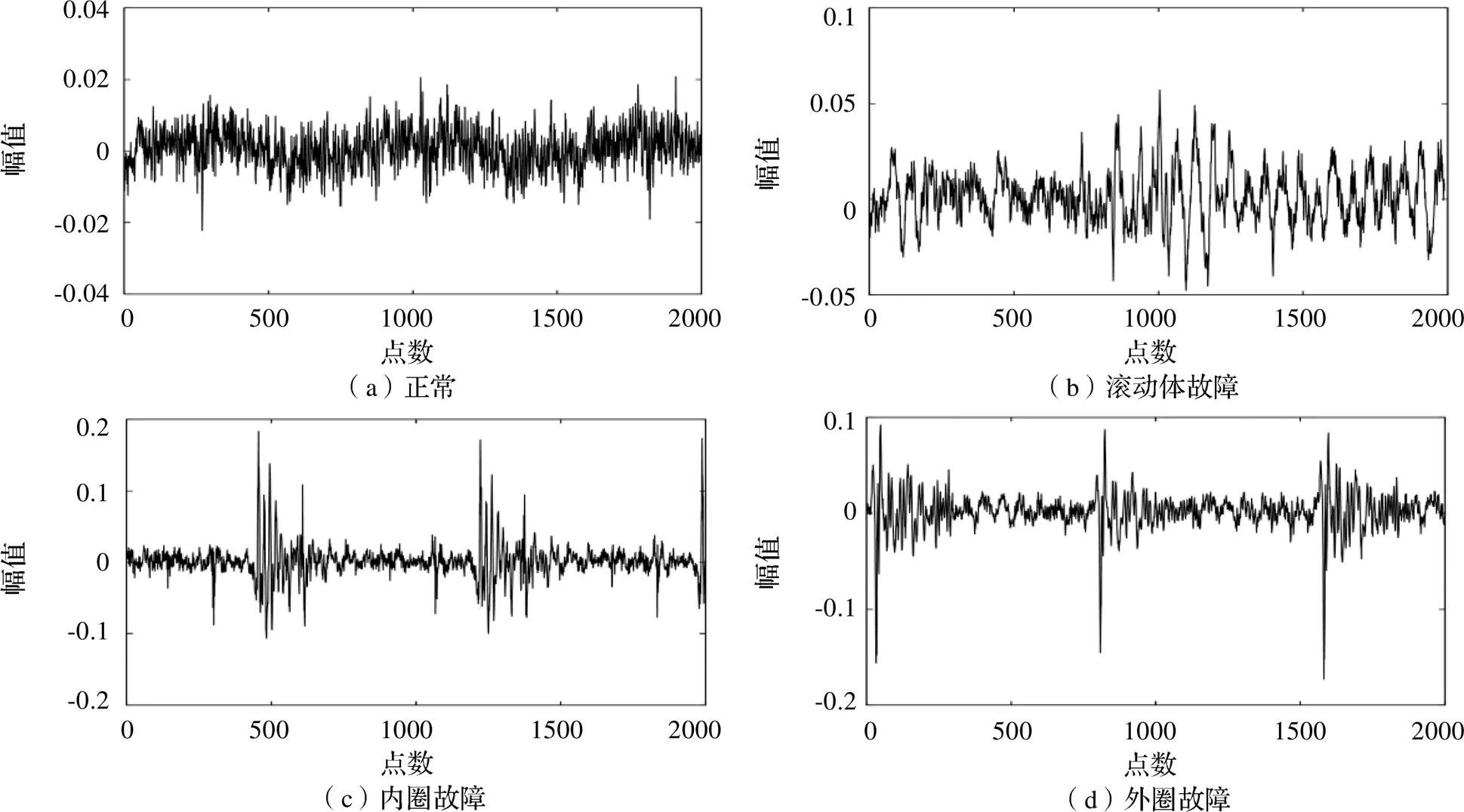
图5 四种轴承状态波形图

3.3 结果分析

为了测试本文模型的性能，在同一数据集下使用经典CNN模型（AlexNet、VGG）以及CNN-SVM进行轴承故障诊断，计算结果如表2所示，所有模型输入均为原始一维振动信号，模型初始学习率和批大小为0.001和64，PSO参数设置优化参数dim＝2，粒子数＝5，权重参数＝0.8；粒子群学习因子1＝1.5，2＝1.5，1＝0.8，2＝0.8。最大迭代次数10交叉概率0.5，遗传概率0.5。每次计算100 epoch，计算5次取均值作为计算结果。

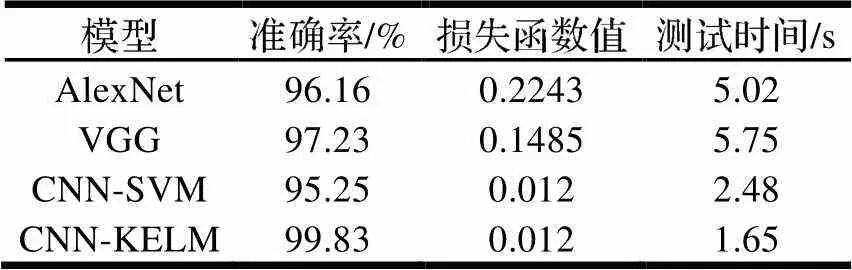
表2 同模型测试结果

由表2可知，同工况下，提出的CNN-KELM模型测试集有更好的预测精度及较短的训练时间，CNN-SVM和CNN-KELM损失函数值相近，但预测精度差，AlexNet和VGG预测精度和训练时间相比本文算法效率更低下、预测精度更差。表明提出模型在故障诊断方面的优越性。

3.4 变工况下的实验及分析

为进一步试验提出模型在变工况数据集中的鲁棒性，改变第3.1节中的试验载荷（其中一个转子换成负载，载荷标记为1），减少试验载荷模拟轻载工况（两个正常转子，载荷标记为0），更改后的试验如图6所示。试验操作不变，分别采集不同运行状态轴承在1600 r/min、1200 r/min转速下的振动信号，其中几种状态信号如图7所示。

3.4.1 变工况数据说明

组合第3.2节中样本数据共同构成变工况下的滚动轴承故障样本数据集，分别包括转速1600 r/min下的正常数据、滚动体故障、内圈故障、外圈故障数据，包含轻载重载两类，同时包括转速1200 r/min下的轴承内圈、外圈和滚动体在重载工况下的数据，并标签化处理，总共十种类别，共10000个样本。每个类别随机选择样本数据划分训练集、验证集和测试集，具体样本描述如表3所示。

图6 机械故障模拟实验台（低载）

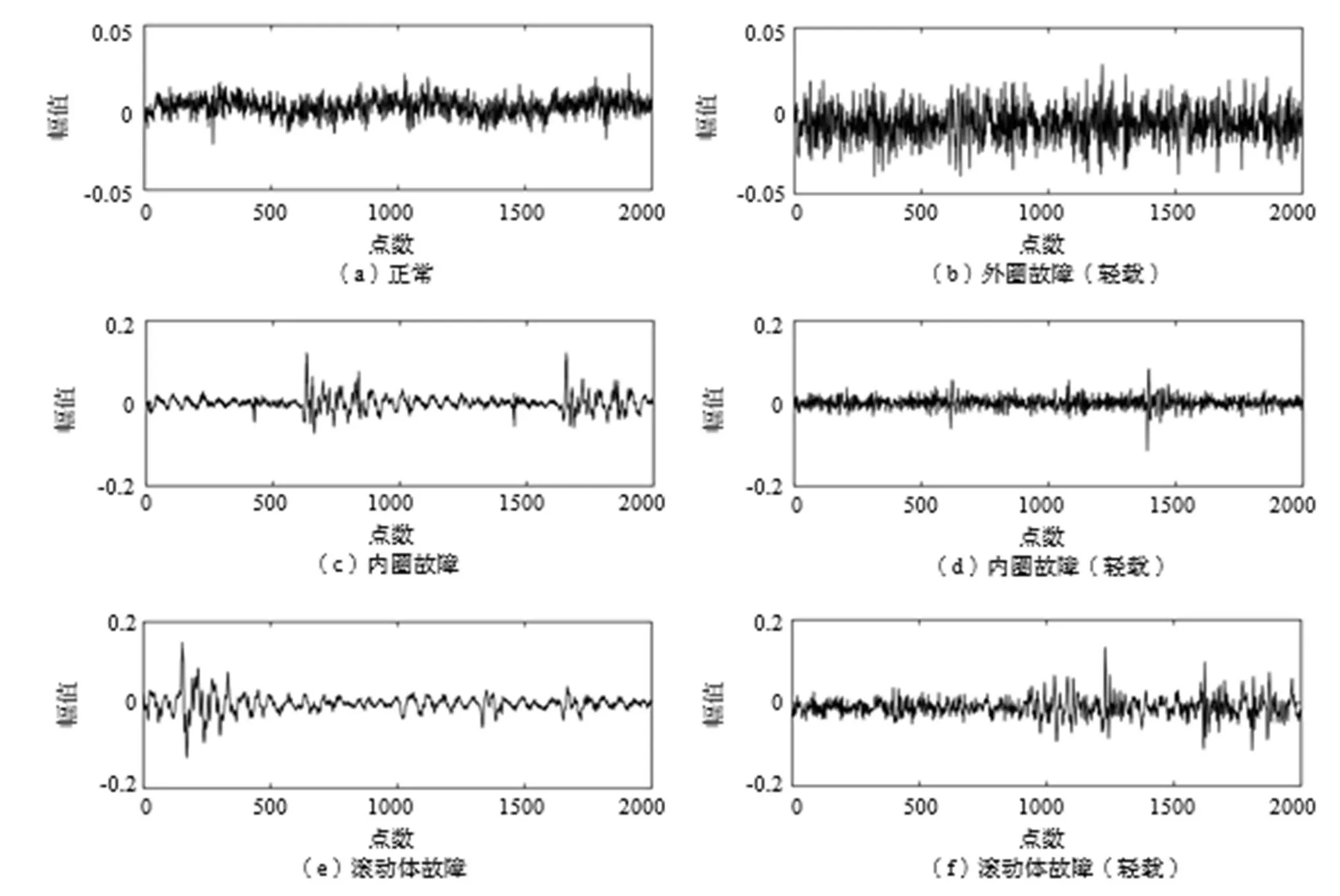
图7 各种轴承状态波形图

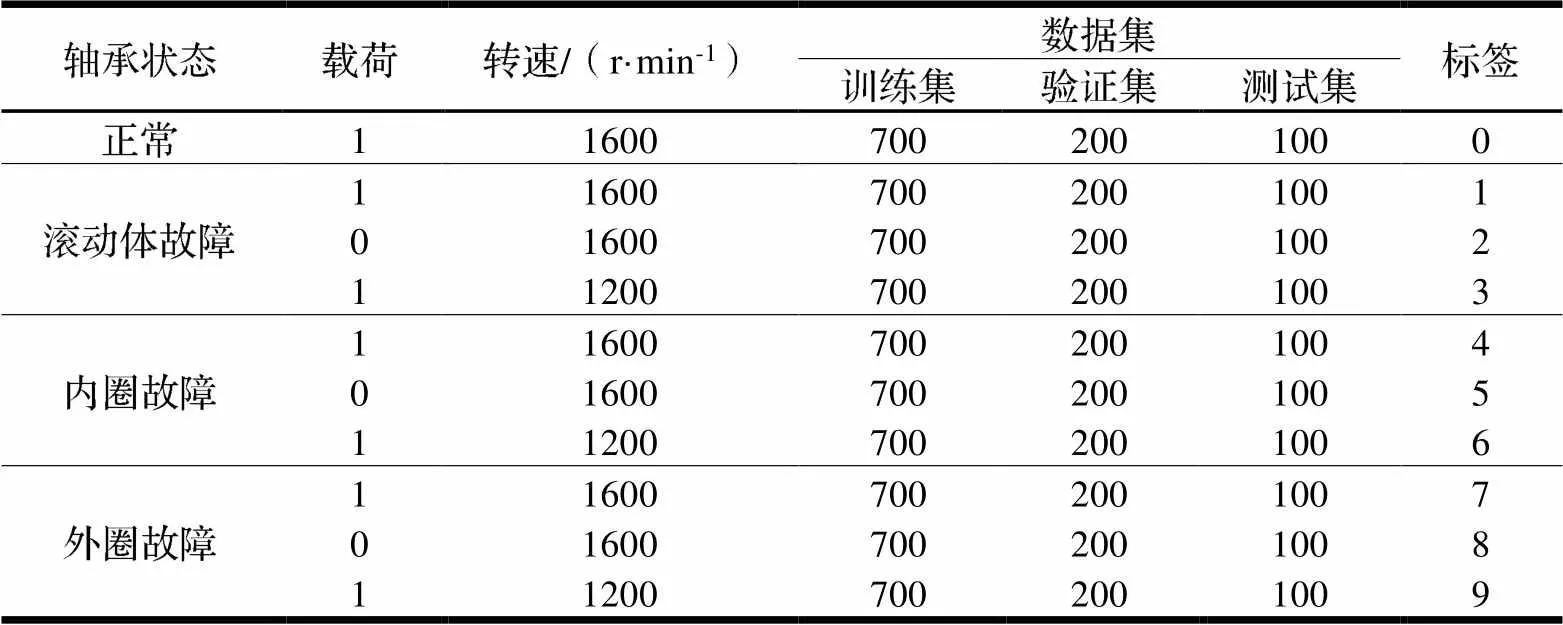
表3 变工况下的滚动轴承故障样本组合

3.4.2 变工况结果分析

由表4可知，提出的CNN-KELM模型测试集平均准确率达到99.85%，高于其他模型的平均准确率且损失函数最小，说明模型实际输出与预测差值较小。比其他模型测试时间更短，表明了提出模型具有学习速度快且诊断更精确的优点。表明本文算法具有较高的故障识别率，同时能较好应对不同工况，鲁棒性好。

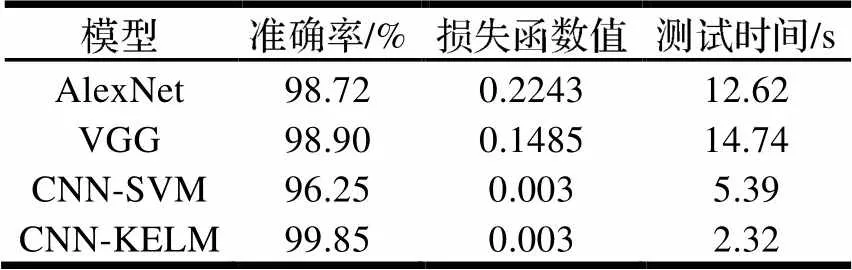
表4 变工况下不同模式测试集计算结果

4 结论

本文提出了基于CNN-KELM混合神经网络的滚动轴承智能诊断方法，结合CNN和KELM网络的优势，直接从原始振动信号中自适应提取特征信息，减少人工特征提取的不确定性，通过实验测试得出如下结论：

（1）提出的CNN-KELM方法在同工况的滚动轴承故障模式分类中准确率达到99%以上，比其他模型的准确率更好；

（2）在不同转速、不同载荷的变工况下的轴承故障诊断中，所提方法平均准确率达99%以上，损失函数值比其他模型更低，能更好地适应变工况的环境。

[1]胡君林，赵炎堃. 基于改进HVD和包络谱的轴承故障诊断方法[J]. 机械，2020，47（1）：30-34.

[2]陈保家，黄伟，李立军，等. 最大重叠离散小波包变换边际谱特征在齿轮故障诊断中的应用[J]. 西安交通大学学报，2020，54（2）：35-42.

[3]李伟. 基于EEMD和Teager能量算子的行星齿轮箱故障特征提取研究[J]. 噪声与振动控制，2020，40（4）：109-113，119.

[4]郭亮，高宏力，张一文，等. 基于深度学习理论的轴承状态识别研究[J]. 振动与冲击，2016，35（12）：167-171.

[5]张绍辉. 基于多路稀疏自编码的轴承状态动态监测[J]. 振动与冲击，2016，35（19）：125-131.

[6]曲建岭，余路，袁涛，等. 基于一维卷积神经网络的滚动轴承自适应故障诊断算法[J]. 仪器仪表学报，2018（7）：134-143.

[7]HUANG G B，ZHU Q Y，SIEW C K. Extreme learning machine： a new learning scheme of feedforward neural networks[C]. IEEE international joint conference on neural networks，2004. Proceedings， IEEE，2005，2：985-990.

[8]皮骏，马圣，杜旭博，等. 基于BQGA-ELM网络在滚动轴承故障诊断中的应用研究[J]. 振动与冲击，2019，38（18）：192-200.

[9]宋佳，石若凌，郭小红，等. 基于核极限学习机的飞行器故障诊断方法[J]. 清华大学学报（自然科学版），2020，60（10）：795-803.

[10]崔鹏宇，王泽勇，邱春蓉，等. 基于多尺度排列熵与双核极限学习机的滚动轴承故障诊断方法[J]. 电子测量与仪器学报，2019，33（5）：142-147.

[11]Zhang W，Peng G，Li C，et al. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals[J]. Sensors，2017，17（2）：425.

[12]Zheng L, Wang J, Wang Z, et al. Research on Novel Bearing Fault Diagnosis Method Based on Improved Krill Herd Algorithm and Kernel Extreme Learning Machine[J]. Complexity，2019.

[13]Y. Behdinan，D. Huang，J. Yan. A novel extreme learning machine classification model for e-nose application based on the multiple kernel approach[J]. Sensors，2017，17（6）：1434.

[14]苏一丹，麻晓璇，覃华，等. 基于柔性多面体的最优核极限学习机算法[J]. 计算机工程与设计，2020，41（9）：2454-2459.

[15]Kennedy J.，Eberhart R. Particle swarm optimization[A]. In： Proceedings of the IEEE International Conference on Neural Networks IV，1995：1942-1948.

[16]ZhangXin-yuan，Hu Xiao-min，Lin Ying. Comparative analysis of performance of genetic algorithm and particle swarm optimization algorithm[J]． Journal of Computer Science and Technology，2014，8（1）：90-102.

[17]Sun H，Yang J，Wang L. Resistance Spot Welding Qual⁃ity Identification with Particle Swarm Optimization and a Kernel Extreme Learning Machine Model[J]. Interna⁃tional Journal of Advanced Manufacturing Technology，2016，91（5）：1-9.

Application of GAPSO-KELM in Rolling Bearing Fault Diagnosis

FANG Junhao，CHEN Zhengkun，CHEN Baojia，CHEN Xueli

(College of Mechanical and Power Engineering, China Three Gorges University, Yichang 443002, China)

In order to reduce the dependence of fault feature extraction on signal processing methods and artificial experience, reduce the computational complexity of diagnosis model, and effectively improve the diagnosis accuracy, a rolling bearing fault diagnosis method combining convolutional neural networks (CNN) and kernel extreme learning machine (KELM) is proposed. Firstly, the original vibration signals of rolling bearing under different fault modes are directly processed by sections to construct training set, verification set and test set. Secondly, CNN convolution operation is used to extract the features and pool operation is used to extract the simplified feature information. Finally, the extracted features are used to train KELM, and the genetic particle swarm optimization (GAPSO) algorithm is used to set the penalty coefficient C and kernel parameterof KELM to obtain the fault diagnosis model. In order to evaluate the effectiveness of the method, experiments are carried out under the same and off-design working conditions, and compared with CNN-SVM, Alexnet and VGG methods, the results show that the method has better accuracy and stability.

convolutional neural network；rolling bearing；kernel extreme learning machine；fault diagnosis

TH133.33

A

10.3969/j.issn.1006-0316.2021.03.002

1006－0316 (2021) 03－0009－08

2020－10－09

国家自然科学基金（51975324）；湖北省重点实验室开放基金（2020KJX02）；宜昌市应用基础研究项目（A19-302-08）

方俊豪（1993－），男，湖北孝感人，硕士研究生，主要研究方向为机械故障诊断、深度学习。*通讯作者：陈保家（1977－），男，湖北孝感人，博士，教授，主要研究方向为机械装备状态监测、故障诊断及可靠性评估，E-mail：987794348@qq.com。