基于CFD的真空阀流固耦合及热应力分析
彭川桃,罗阳*,,周博,黄斐月,宋敏
基于CFD的真空阀流固耦合及热应力分析
彭川桃1,罗阳*,1,周博1,黄斐月1,宋敏2
(1.四川大学 机械工程学院,四川 成都 610041;2.九川真空科技(成都)有限公司,四川 成都 610213)
以大型高温真空阀门的主动冷却为研究对象,建立了阀体和流体的三维耦合分析模型。首先考虑阀体内冷却通道受稳定水流及均匀热流载荷的共同作用,分析了该共轭传热问题的控制方程。然后利用CFD的方法计算得到了在不同进水流速下流体的流场和阀体冷却效果。最后选择最优流速下的稳态温度场作为热载荷对阀体结构进行热应力分析,得到了阀体结构的应力云图与位移云图。通过对云图的分析证明了方案设计的合理性,并为今后的改进提供理论依据。
流固耦合;控制方程;CFD;热应力
随着真空行业的发展,真空系统的应用越来越广泛,对真空设备的要求也随之提高。真空阀门作为在真空系统中用来改变气流方向、调节气流量大小、切断或者接通管路的元件,在真空系统中至关重要。由于真空阀门关闭件多采用橡胶密封圈来密封,在高温工况下,为防止密封圈失效,必须对阀体进行冷却处理。实际工程中,高温阀体的水冷主要采用冷却流道内的液体带走热量的主动冷却方式。该过程包括流体的流动和传热、阀体本身的热传导以及流体和阀体交界面的传热,是一个典型的流固耦合传热问题。流固耦合问题属于计算流体动力学(Computational Fluid Dynamics,CFD)范畴[1],本文使用CFD方法,通过求解流体力学的控制方程,对研究对象进行模拟和分析。
本文以一大型真空闸阀的阀体为研究对象,阀体高温侧通过真空管与真空炉连接,真空炉烘烤温度约400℃,要求阀体密封面Г(图1)温度不超过200℃,采取主动冷却方式降温,其中,阀体外形尺寸为1290 mm×145 mm×225 mm,真空管道外形尺寸为1290 mm×25 mm×170 mm,二者中央有1140 mm×45 mm的通口。阀体高温侧的阀壁上有两条连贯的8 mm的冷却通道,冷却液为水,如图2所示,忽略阀体的热辐射及内腔的对流换热,阀体多余热量全部由冷却水带走,已知入口水温为20℃,水压为0.4 MPa。

图1 阀体密封面示意图

A/B.进水口 C.出水口
1 数学模型
考虑高温面受到真空炉稳定热流载荷的阀体在冷却水流的作用下的流固耦合传热[2]问题,该过程包括管道流体的流动与传热、流体和固体界面的传热和固体内部的热传导。耦合传热主要体现在流固交界面热传导和热对流的耦合,交界面处的流体与结构相互作用,此处的边界条件由动态换热决定而不能预先设定,必须联立求解。控制方程主要包括固体的导热方程,流体的质量、动量和能量方程[3]等。
1.1 流体控制方程
考虑冷却管道内为不可压缩流动,流场的控制方程为[4]如下。
连续方程:
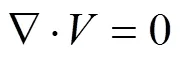
动量方程:
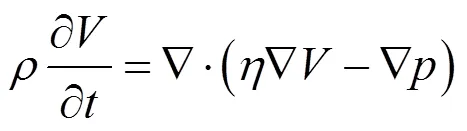
能量方程:
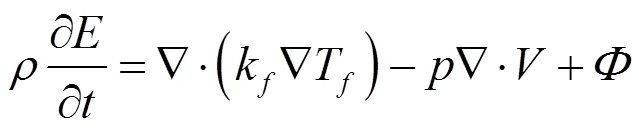
冷却水入口流速初设为=1 m/s,查水的物性表有=20℃时,=998.2 kg/m3,=1.004×10-3Pa·s,特征长度=8×10-3m,计算出入口雷诺数为:
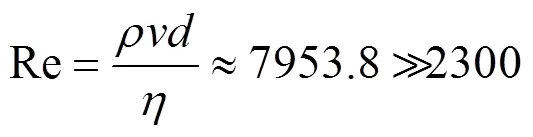
因此管道流场属于湍流流动,湍流模型采用标准的-方程[5]。
1.2 固体导热方程
考虑固体结构的初始温度为室温,结构外壁面的左表面有稳定热流载荷,其固体导热方程为[6]:
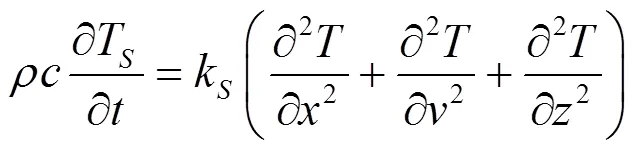
初始温度0=20℃,有:
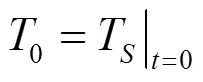
稳定热流载荷输入面(图3)边界条件:
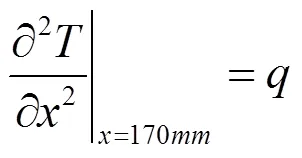
在冷却管壁面,由温度和热流的连续性条件有:
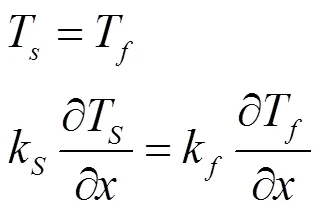
式中:T为固体温度,℃;k为固体导热系数,W/(m·℃);为单位面积的热流量,W;为比热容,kJ/(kg·K)。
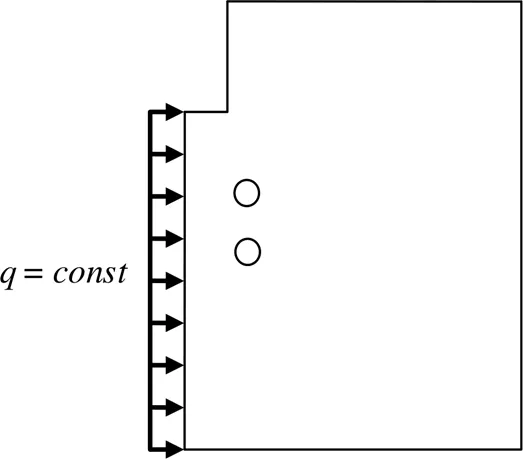
图3 热流载荷图
1.3 热应力应变方程
由此前的固体导热方程可得到结构的温度场,将其联合弹塑性力学边界条件和初始条件可求解得到应力场和应变场,该过程为弹塑性结构的热应力分析。考虑阀门材料为理想塑性的,其应力应变方程为[7]:
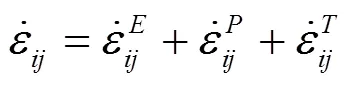

1.4 耦合方程
该流固耦合传热问题遵循基本守恒原则,因此流固耦合交界面处,应满足如下约束方程:
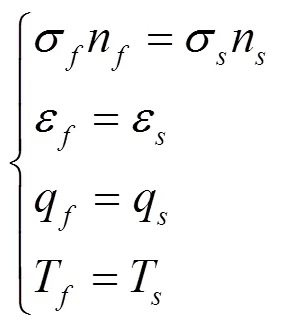
式中:为应力,MPa;为交界面的单位法向量;为应变;为热流量,W;为温度,℃;下标表示流体;下标表示固体。
2 模拟仿真
在流体与固体交界面采用流固耦合法(FSI,Fluid Solid Interaction)进行方程的联立,针对耦合问题ANSYS提供了两种求解算法:多域单代码耦合(MFS,Multi-Field-Single code coupling)和多域多代码耦合(MFX,Multi-Field- Multiple code coupling)。宋宏伟等[8]对这两种算法进行了详细比对,两种方法都是在各个域分别建立交界面,各个物理场的矩阵单独求解直至交界面之间的传递载荷收敛为止,但是MFS方法是在同一求解器中完成多物理场耦合计算,可以节约计算资源。此外,CFX与ANSYS结构力学产品具有天然双向连接,使最复杂的流固耦合问题处于简便使用的环境内[9],可方便随后的温度场分析及结构力学模拟。因此,本文采用MFS方法在CFX求解器中研究该真空阀的流固耦合问题,结合工具Steady-State Thermal和Static Structural分别做稳态温度场分析和稳态结构力学模拟。
2.1 模型网格
将阀体模型导入Workbench中的CFX工作栏,设置求解器为CFD,在DM工具中对模型进行合并固体域、设置边界面和填充流体等前处理工作。对流体固体分别划分网格,网格类型为四面体单元,其中固体域网格具有269022个结点、171569个单元,流体域网格具有20520个结点、9753个单元。
2.2 物性参数
分析模型中固体域材料采用中碳钢(C0.4%),流体域采用液态水。为在计算机上实现问题的模拟分析,需要定义固体和流体的物理性能参数,如表1、表2所示。

表1 碳钢(C0.4%)温况-物性参数表
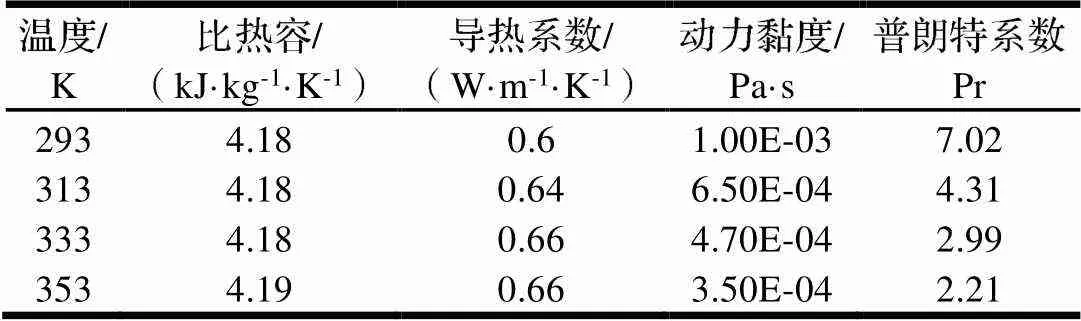
表2 液态水温况-物性参数表
2.3 边界条件
对于流体,考虑到方便循环水冷装置的配置,将A和B两个进水口条件设为一致,包括入口流速、入口水温和出口水压。其中入口流速根据经验从1~5 m/s分五次等差进行试算,入口水温均设置为20℃,出口水压设置为均压0.4 MPa。
对于固体,将热流载荷面设置为恒温400℃,由于辐射带走的热量较小,在此不考虑辐射的影响,再加上阀体内部为真空环境,可以忽略对流换热,于是设置除高温面的其他外表面和内表面为绝热。对于流固交界面,考虑本模型中水为理想流体没有粘性,整个流场包括边界都没有剪切作用,于是将其设定为无滑移边界面[10]。
3 结果与分析
3.1 流速分析
以不同入口流速作为加载,其他条件不变的情况下分别模拟分析得出了流体出口流速、出口温度和密封面Г温度等衡量冷却效果的重要物理参数的变化,如表3所示。可见,出口流速大致与入口流速呈现2:1的关系,这是因为流道由两个8的通道汇流而成,且本研究模型为满足连续方程的牛顿流体。另外,当入口流速等于1 m/s时,出口水温为112.4℃,处于高温高压的状态,流体的温升过大。随着流速的增加,出口水温不断下将,流体温升不断减小,Г面温度不断下将,相同时间内被带走的热量增多。
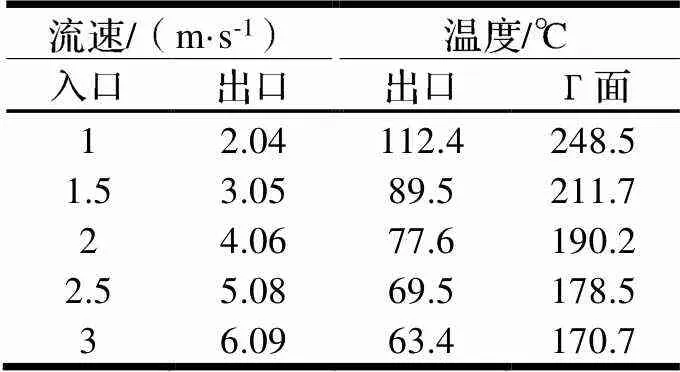
表3 冷却效果参数表
根据流场出口温度和Г面温度随着入口流速的变化而变化绘制了图4。随着入口流速的增加,出口温度曲线和Г面温度曲线的斜率都在降低,说明流体来不及带走更多的热量,即冷却能力随着流速的增加在降低。如图4所示,在入口流速为1.66 m/s时,Г面温度到达临界点,为了方便配制水泵且考虑Г面温度安全系数,选择2 m/s作为最优入口流速。下面将展开最优入口流速状态下的详细分析。
流体的流线如图5所示,可见:从入口到弯道这段水流速度基本保持2 m/s,变化不大;在弯道处,水流速度突变,其中弯道内侧流速减小、弯道外侧流速增加;当通过弯道后,水流速度回到稳定状态,保持在2 m/s左右;当水流通过汇流处时,流速骤增,此处流体中心的速度达到4.6 m/s,这是流量不变但横截面积骤减所致;最后水流速度又回到稳定状态,保持在4 m/s左右。
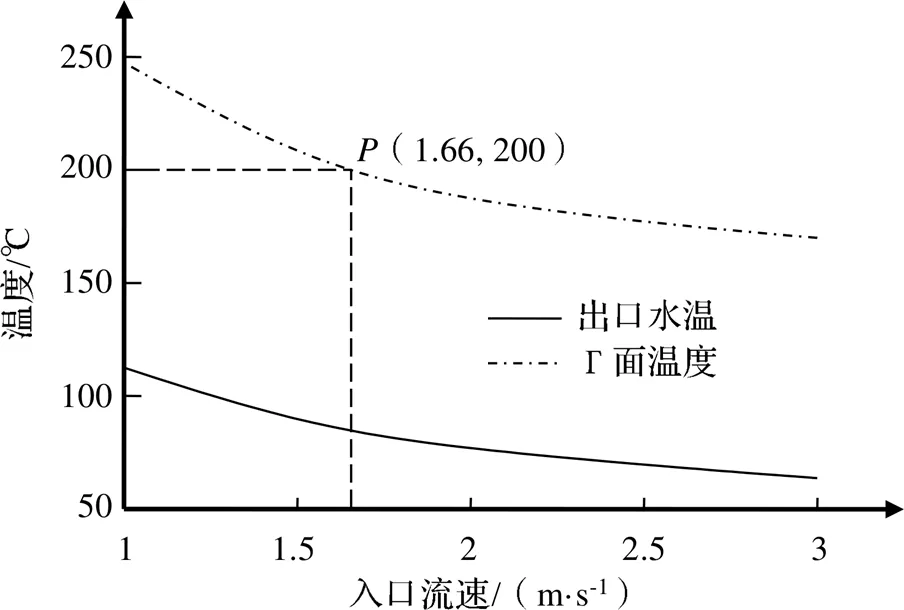
图4 冷却效果曲线
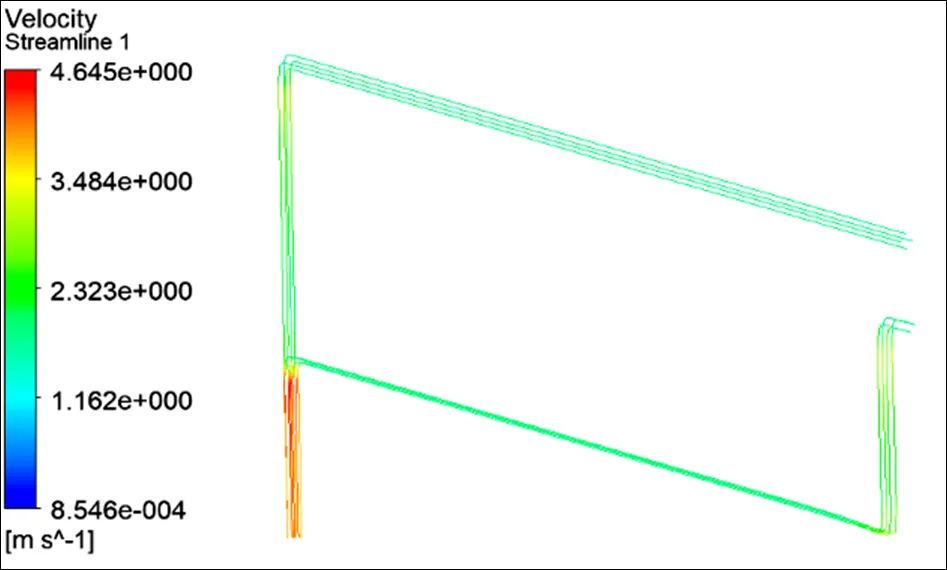
图5 流体流线图
3.2 温度场分析
流体的温度场分布如图6所示,冷却水在管道内逐渐升温,且等值面的宽度基本一样,说明冷却水温升速度变化不大,即吸热力稳定。这也与表2中流体的热导率变化不大相吻合。在流道出口的附近,流体外表的温度达到了81℃,但平均出口温度在77.6℃左右。在靠近水冷堵头的两端,水流停止,形成局部高温,此处水温稳定在53.9℃左右。在靠近出口的直流道起点附近也形成了局部高温,温度在70.9℃左右,形成机制和水冷堵头附近一致。
阀体的温度场分布如图7所示,由于结构具有对称性,截取1/2作分析。观察可知,密封面Г处温度在190.2℃附近,满足密封圈工作要求。由于冷却管道位于左侧阀壁内,从壳体左侧高温端面到右侧低温端面的温度变化最为剧烈,这个区域包含了图中的所有温度带。其中,左端面处于最高温度带;冷却管道的内表面处于最低温度带,且内表面前端至后端的温度逐渐升高;密封面Г处于第二和第三温度带之间,在常规橡胶圈的工作温度范围内;阀体主体结构位于第七温度带,稳定在320℃左右。
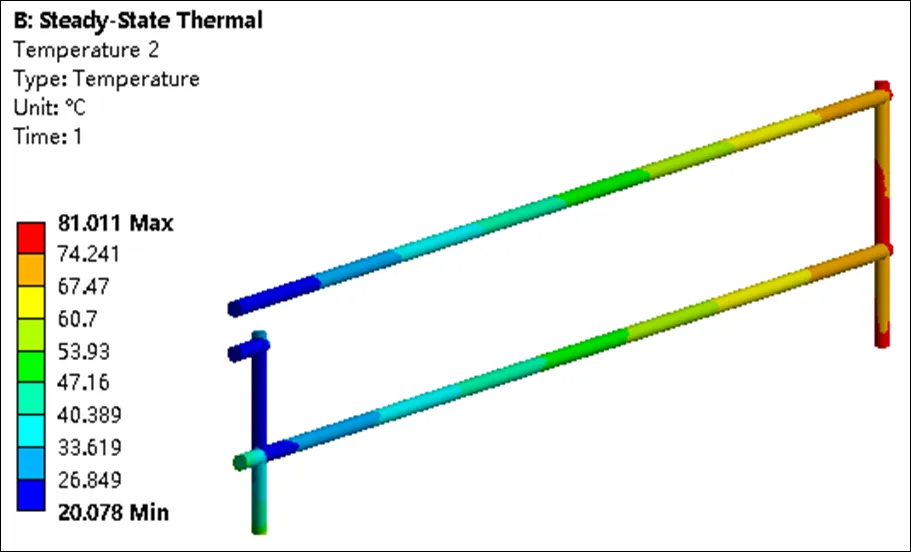
图6 流体温度场云图
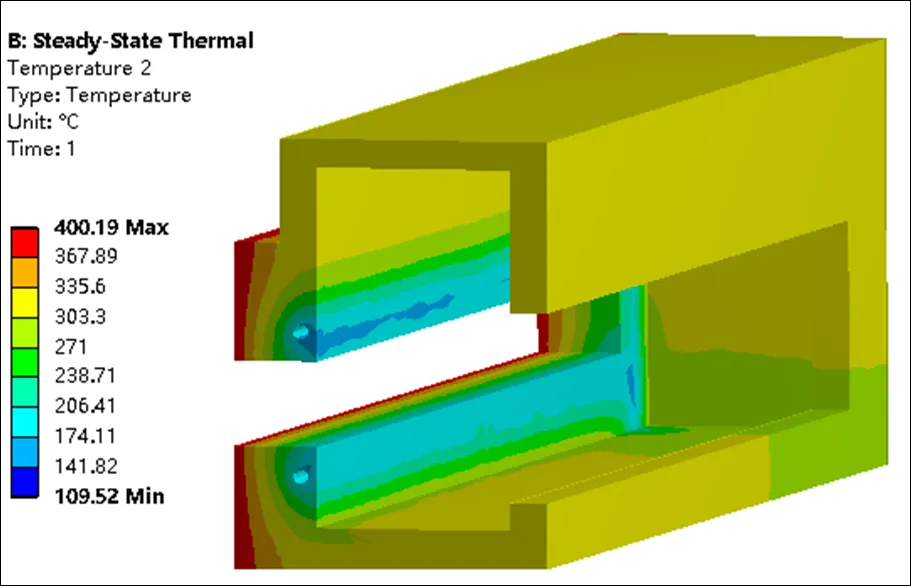
图7 阀体温度场云图
3.3 应力应变分析
为研究流场和温度场对结构应力的耦合作用,截取包含流道的固体应力云图如图8所示。观察流道附近的应力变化可知,流场对结构的应力影响微乎其微,阀体的应力主要来源于热流载荷。由于管道拐角区域或管道末端存在尖角,管道的应力主要集中于此,因此在管道设计上可以考虑全部打通孔,在必要部位采用水冷堵头封流。此外,由于阀体底面为安装面,被固定的安装面不能产生变形,所以应力主要集中在阀体底面,但由于底面属于非重要部位,故可不更改安装方案。最后,应力最高点位于阀体的棱角部分,需要对棱角部位进行扩大倒角处理。
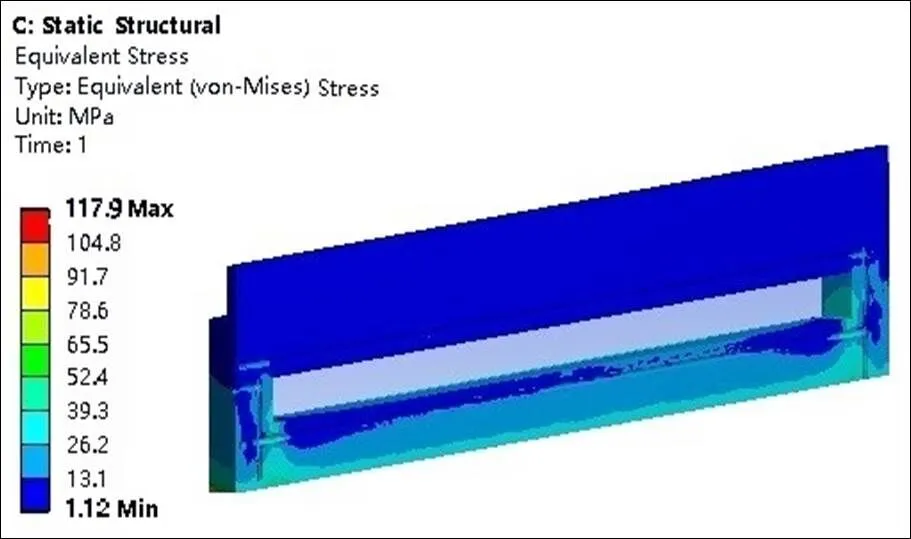
图8 阀体应力截面图
为了使结构变形一目了然,对阀体结构进行连续截断,得到图9。由于阀体底面不能产生变形,所以在热流载荷的作用下,阀体由底端至顶端产生了连续膨胀变形,且应变关于阀体中央基本对称。从两端到中央应变等值面宽度递增,说明越靠近顶端中央的区域变形越大。此外,在等值面经过冷却通道时,变形量出现波动,这主要是考虑管道结构导致阀壁处于薄壁层状态,在同样的温度变化下应变更大,因此设计时可考虑增加壁厚以防止结构破坏。

图9 阀体变形断层图
4 结论
本文首先分析了真空阀门热流固耦合的数学模型,然后通过网格划分、CFX计算、稳态温度场计算、稳态结构场计算等手段,利用已知条件采用基于CFD的数值方法对阀体的流固耦合问题进行模拟仿真和热应力分析,求解得到满足阀体工作温度的最优入口流速为2 m/s,并分析了该状态下流体的流场和温度场以及固体的温度场和热应力应变图,为阀门的设计改进提出了一些意见和建议。后经实验验证,阀门在此冷却条件下能够稳定工作,不会因工况温度高而导致密封圈过早失效。
[1]李星峰,王玲,殷国富. 基于ANSYS-CFX的离心压缩机叶轮流固耦合仿真分析[J]. 机械,2018,45(5):14-18.
[2]张辉平,胡在双. 基于流固耦合传热的摩托车发动机冷却水套优化设计[J]. 机械,2014,41(9):35-39.
[3]陶文铨. 数值传热学[M]. 西安:西安交通大学出版社,2004.
[4]H. K. Versteeg,W. Malalasekera. An Introduction to ComputationalFluid Dynamics[M]. 2nd edition. The Finite Volume Method,Pearson Education,2007.
[5]张健,黄晨光. 方形管耦合传热及管道热应力分布数值模拟[C]. 中国力学学会:第一届高超声速科技学术会议论文集,2008.
[6]M. N. Ozisik.Heat Conduction[M]. New York:Wiley,1980.
[7]刘鸿文. 材料力学[M]. 北京:高等教育出版社,2011.
[8]宋宏伟,纪科星,黄晨光,等. 主动冷却通道热流固耦合三维数值计算及构型应力分析[C]. 中国力学学会:第三届高超声速科技学术会议会议文集,2010.
[9]刘斌. Fluent19.0流体仿真从入门到精通[M]. 北京:清华大学出版社,2019.
[10]王文全,郝栋伟,张立翔. 滑移界面位置对叶轮机械内部旋转流场的影响[J]. 北京理工大学学报,2012(9):890-894.
Fluid-Solid Coupling and Thermal Stress Analysis of Vacuum Valve Based on CFD
PENG Chuantao1,LUO Yang1,ZHOU Bo1,HUANG Feiyue1,SONG Min2
(1.School of Mechanical Engineering, Sichuan University, Chengdu 610041, China;2.JiuChuan Vacuum Technology (Chengdu) Co., Ltd., Chengdu 610213, China)
Taking the active cooling of large high temperature vacuum valve as the research object, the three-dimensional coupling analysis model of valve body and fluid is established. Firstly, the governing equation of the conjugate heat transfer problem is analyzed on the basis of the fact that the cooling channel in the valve body is affected by the steady flow and uniform heat flow loads. Then the flow field and cooling effect of the valve body at different inlet velocities are calculated through CFD method. Finally, the static temperature field at the optimal flow rate is selected as the thermal load to analyze the thermal stress of the valve body structure, and the stress and displacement cloud diagrams of the valve body structure are obtained. Through the analysis of the cloud image, the rationality of the scheme design is proved, and the theoretical basis is provided for the improvement in the future.
fluid-solid coupling;governing equation;CFD;thermal stress
TB756
A
10.3969/j.issn.1006-0316.2021.03.003
1006-0316 (2021) 03-0017-06
2020-09-07
工信部智能制造综合标准化与新模式应用项目:高真空分子泵智能制造车间(2016062);四川省科技厅项目:大型智能环境模拟设备制造技术及应用(2016GZ0159)
彭川桃(1996-),男,重庆人,硕士,主要研究方向为CAE仿真。*通讯作者:罗阳(1969-),男,四川成都人,博士,教授,主要研究方向为CAE仿真,E-mail:drluoyang@scu.edu.cn。

