金融投资组合理论及在我国证券市场的实证分析

娄静 对外经济贸易大学

金融发展与证券市场息息相关，特别是证券投资行业，在金融发展的影响下，表现出迅猛发展趋势。但就证券投资行业现状而言，投资管理不满足证券投资发展需求，阻碍了证券市场的成熟发展步伐。为更好地应对证券投资风险，建议行业工作者结合我国证券市场特点，合理开发应用金融投资组合理论。

一、金融投资组合理论分析

就狭义角度而言，金融投资组合理论是指均值-方差模型及相关拓展理论[1]；就广义角度而言，金融投资组合理论是指均值-方差模型、套利定价理论、资本资产定价理论（CAPM）等理论[2]。无论是狭义概念还是广义概念，金融投资组织理论的定位与研究内容不变：探究投资者如何制定投资方案，在收益稳定的情况下获取最高收益；探究投资者如何调整资产组合、选择合适资产投资，以实现贴现值最大；建议投资者投资多个行业，持有不同资产，以降低投资风险[3]。基于上述研究内容，金融投资组合理论在一定程度上，可为我国证券市场发展建设提供理论借鉴。

随着金融市场的发展，金融投资组合理论的研究与实践更为丰富，金融行业工作者以广义的金融投资组合理论为重点，探究其对实践工作的指导。就学术界研究现状而言，研究学者关于金融投资组合的研究表现出趋同性，集中于CAPM 方面，CAPM 异常现象引发金融行业从业者与专家学者的广泛思考。在20 世纪70 年代后，金融市场出现难以通过CAPM 理论介绍的金融投资活动。在此基础上，为推动我国证券市场发展，合理开发利用金融投资组合理论，需开展相应实证研究，探究金融投资组织理论的可行性与局限性，切实发挥理论指导作用，推动证券市场可持续发展。

二、金融投资组合理论在我国证券市场的实证研究

（一）实证研究对象

结合上述理论分析结果，本文在上海股市中选择合适股票作为样本，对股票数据进行处理与分析，总结证券市场发展规律，验证其是否与CAPM 模型一致，进而评估金融投资组合理论的适应性。在A 股市场中，随机抽取60 支2013-2018 年的股票，根据CCER 数据库的存储数据，获取60 只股票的周收盘价及收益率，作为样本数据展开实证分析。实证分析选择两阶段回归法，结合CAPM 模型，分别通过时间序列法、横截面检验法处理样本数据。

（二）实证研究过程

1.时间序列法检验

在时间序列检验中，选择BJS 方法处理样本数据，将样本数据划分为三个时间段，分别为2013 年1 月至2014 年12 月；2015 年1 月 至2016 年12 月；2017 年1 月 至2018 年12 月。三个时段的样本数据处理如下：

（1）单个股票的β 系数。

以每只股票在第一时段的数据为基础，进行β 系数的计算，模型如下：

其中，Rit与Rft分别是指每只股票t 时间内的周收益率及无风险收益率；RMt是指市场指数在t 时间内的周收益率；αi与βi是指模型计算的估计参数；εit是指残差项。

（2）股票组合及其收益率。

根据计算的每只股票β 系数，将60 只股票按照从大到小的顺序排列，平均划分为20 组。就目前我国证券市场而言，投资者通常选择等额法制定投资组合方案。在此基础上，实证分析中选择第二时段的样本数据，计算股票组合收益率，使计算结果更贴合证券市场实际数值。计算方法为简单算术平均法，公式如下：

其中，Rpit是指在t 时刻时，第i 个股票组合获得的收益率；Rmt是指在第i 个股票组合中，第m 只股票在t 时刻获得的收益率。N是指股票数量。在本次实证研究中，N 为3，m ≤3。

（3）组合股票β 系数。

在明确最优股票组合的基础上，可使用时间序列模型，计算组合股票的β 系数，计算模型如下：

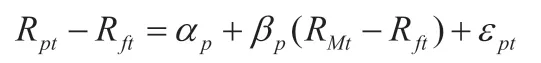
其中，Rpt是指某个股票组合在t 时间内的周收益率；Rft与RMt同上；αp与βp是指模型计算的估计参数；εpt是指残差项。

（4）收益与风险关系。

在股票组合的收益与风险关系探究中，选择第二时间段的股票组合β 系数为样本，开展相关分析，检验模型如下：

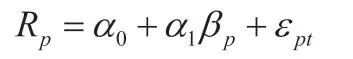
其中，Rp是指平均收益率；α0与α1是指模型计算的估计参数；βp是指股票组合的β 系数；εpt是指残差项。

2.横截面检验

横截面检验方法的模型如下：

其中，Rp、βp同 上；β2p是股票组合β系数的平方；σp是指标准差；α0、α1、α2、α3均模型计算的估计参数；εpt是指残差项。

在使用该模型进行验证时，应满足如下假设条件：其一，风险与收益有线性关系，要求E（α2）=0；（2）仅可通过β 系数实施风险评估，其余风险内容不可作为股票组合定价的影响因素，此时E（α3）=0；（3）在股票投资组合中，高风险，意味着投资者期望股票投资组合获得更高收益，此时；（4）E（α0）=Rf。结合时间序列检验获取的数值，应用上述模型与条件实施检验。

（三）实证研究结果与分析

1.实证分析结果

按照上述实证分析流程，可获取60 只股票、β 系数及收益率等计算结果。根据回归分析结果可知，股票组合的风险与证券市场风险存在正相关关系。在20 个股票组合后，10 组拟合系数超过0.7，8 组拟合系数在0.4-0.7 之间，仅有2 组拟合系数低于0.4。可见，实证分析的结果具有可信度。

在收益与风险关系研究中，所有股票的无风险收益率非0 非负数，由此可见，沪市股票市场的风险和收益有线性关系，风险会影响沪市股票定价，这与金融投资组合理论相符。但在实证检验中，βp及估计参数均未达成t 检验条件，且回归分析计算的拟合系数为0.000039。可见，该结论不具备可信度，说明系统性风险和收益无显著线性关系，与CAPM 理论不相符。可见，在证券市场的股票定价中，还存在其他风险影响因素，发挥重要作用。在应用金融投资组合理论分析我国证券市场时，计算结果存在较高随机性。结合我国证券市场发展实际，探究该实证分析结果的原因为市场正在发展中，与西方已经成熟的证券市场存在差异。

在横截面检验中，α0为正数，结果与时间序列检验相同，说明上海股票市场无风险收益率是正数，该结论成立。α1为负数，α2为正数，证实风险与收益无显著关联；α3为负数，证实非系统性风险和收益有关联。总的来说，CAPM 理论在上海股票市场中的应用存在局限性。

2.结果讨论与分析

结合上述实证分析结果可知，金融投资组织理论在我国证券市场的应用存在局限性，分析该问题出现的原因如下：（1）在数据处理时选择方差作为计算指标，存在一定理论性，与证券市场实践不符；（2）CAPM理论的所有假设条件均涉及时间，获得的股票组合为静态分析结果，与证券市场的动态变化现状不符；（3）指标的计算以历史数据为基础，在证券市场实践分析中的应用存在一定风险，使股票投资的收益率计算出现偏差，进而影响投资效益。为有效解决金融投资组合理论的局限性问题，本文提出如下建议，以推动我国证券市场健康发展，加速市场成熟。

（1）深化资产收益率研究。在金融投资组合理论应用中，关于资产收益率的概念、风险、风险影响机制、计算方法等内容的研究，直接关系到资产收益率的计算精度。金融行业从业者与专家学者应深化资产收益率的相关研究，以金融投资组合理论的套利定价理论为基础，进一步明确风险因子的内涵与定义，并从宏观角度入手，分析预测当前经济形势，为确保经济形势预测的准确性，金融行业从业者可直接借鉴权威部门公布的调研数据，再结合所在行业的前景预测结果，综合评估资产收益率面临的风险，为金融投资提供参考。

（2）准确预测资产收益率。资产收益率是金融投资组合理论应用的关键指标，因企业生产中产品的生命周期、环境、市场等多种因素影响产品销售成果，建议证券行业从业者将上述影响因素纳入资产收益率计算范畴，将其与Logstic 模型等理论整合，利用马尔科夫状态转移矩阵构建资产收益率的计算模型，在综合评估各项因素影响的基础上，根据企业产品的特点及产品市场的销售状况，明确产品销售的不同时期，准确评估并统计分析企业在各个时期的收益，应用加权平均法进行处理，即可获取企业准确的资产收益率，为金融投资提供参考。同时，在进行收益率计算与预测的过程中，金融行业从业者应将企业的新增利润增长点纳入分析范畴，并根据新增的利润增长点，修正收益率，提高计算结果的精度。

通过上述措施的实施，投资者可根据风险评估值与资产收益率计算结果，进行最优投资组合模型的分析，模型求解后，即可获取最优金融投资组合决策，实现金融投资组合理论的有效开发利用，实现投资者与被投资者的合作共赢。