Nonlinear Quasi-Bessel Beam Generation Based on the Time-domain Digital-Coding Metasurface

FANG Zuqi CHENG Qiang CUI Tiejun

(State Key Laboratory of Millimeter Waves, Southeast University, Nanjing 211189, China)

Abstract:A quasi-Bessel beam is a type of nondiffracted beam commonly used in microwave and optical fields.Although numerous methods have been proposed for quasi-Bessel beam generation,they are valid only in linear systems,indicating that the generation of nonlinear quasi-Bessel beams remains a major challenge.Thus,we propose a new approach to produce quasi-Bessel beams at high-order harmonics based on the time-domain digital-coding metasurface,which is utilized to achieve accurate control of the phase profile at the nonlinear frequencies via proper coding strategies.The effect of phase discretization is also analyzed in detail.The simulation results confirm the validity of the proposed method,which provides a new approach for nonlinear beam manipulation.

Key words:Time-domain digital coding metasurface;Bessel beam;Nonlinear modulation

1 Introduction

Bessel beam is a kind of non-diffracted beam(or localized wave).Due to the collimation and non-diffraction,Bessel beams can concentrate the energy of electromagnetic waves in a small space.It is widely used in many applications such as wireless power transmissions,secure communications,laser micromachining,and so on.

In 1987,Durnin proposed the concept of Bessel beam[1],which derives from a set of solutions of Helmholtz equation in cylindrical coordinates.Theoretically,the ideal Bessel beam is unrealizable since it requires infinitely large energy.However,the truncated Bessel beams,or pseudo-Bessel beams were discovered to remain non-diffracted over a long distance[1–4].In optics,the pseudo-Bessel beam could be produced through circular slit and lens[1],or by the axicon[4].In General,the latter has advantages of high efficiency and convenience,but usually occupies a large space for the beam generation.To overcome this limitation,some new approaches have been developed such as the the Fabry-Perot resonator and reflector.

In contrast,the axicon is no longer suitable for Quasi-Bessel beam generation in microwave region,due to the large size of the overall system,hindering the system integration.As a result,metasurfaces are developed to control the wave front[5,6]to solve those problem.Recently,the antenna array has been proposed to generate Quasi-Bessel beams with low profile[2],but complex feeding networks were required to achieve this goal,and the system bandwidth was highly limited by the antenna performance.In the past few years,a series of studies have been focused on the Quasi-Bessel beam generation based on the metamaterial lens[7,8].The broadband phase profile can be easily implemented by optimizing the metaatoms,thereby the metamaterial lens is especially advantageous for smaller thickness,simpler structure and wider bandwidth compared to other approaches.

In some application scenarios,especially in wireless communications,the Simultaneous Power and Data Transmission (SPDT) is highly desired,as it can extend the operation time and increase the communication distance of portable devices.To further enhance the channel capacity of the whole system and increase spectral efficiency,a number of subchannels at different carrier frequencies are introduced to transmit orthogonal modulated signals.A possible recipe to realize SPDT is to use nonlinear Quasi-Bessel beams at mulitple harmonics.The beams can be focused at different user ends,and achieve efficient energy transfer while transmitting and receiving information between the base-station and users through numerical sub-channels.

However,the nonlinear responses of traditional metamaterials are very weak,making it hard to produce the Quasi-Bessel beams at multiple frequencies.To tackle this problem,time-domain digital coding metasurfaces have been proposed for the nonlinear manipulations of electromagnetic waves during the wave-matter interactions[9–17].By applying the periodic modulations on the reflectivity of the metasurfaces,it is possible to control the harmonic properties accurately,thus paving a new avenue for nonlinear wave control with ultra-high efficiency.

In this paper,we report the generation of nonlinear Quasi-Bessel beam with the time domain digital coding metasurface.By carefully choosing the coding strategy,the harmonic phase profiles of the metasurface can be obtained to synthesize the desired Quasi-Bessel beams,with high energy conversion efficiency from the fundamental frequency to the specified harmonic.The theory is validated by the numerical simulations.

2 Design of Metasurface for Non-linear Quasi-Bessel Beam Generation

From the classical electromagnetic theory,the electromagnetic fields in free space are expressed by homogeneous wave equation as

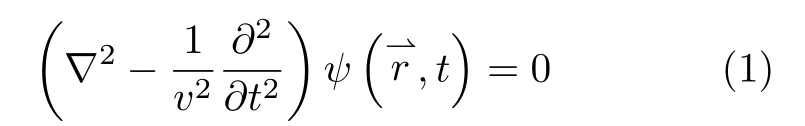
Some solutions of the wave equation allow the localization of electromagnetic waves[1],with the energy concentrated within a specific region.The Bessel beam derives from such a solution of localized electromagnetic wave in cylindrical coordinate system[3].The electromagnetic field of Bessel beam can be expressed as

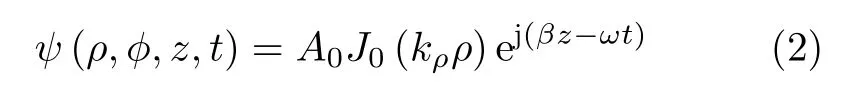
whereJ0() is the Bessel function of the zero order,kρandβare the radial and longitudinal components of the wave vector respectively,which are related by

The angle betweenkρandβcan be expressed as

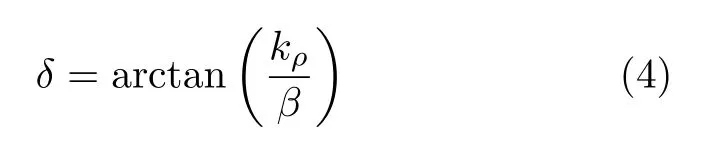
It describes a cone with an opening angle of 2δ[1].

As shown in Fig.1,assume a monochromatic wave incident toward the metasurface at normal direction,in order to get a nonlinear Bessel beam at the frequencyf1,Eq.(3) needs to be rewritten as

Fig.1 shows the angleδbetween the surface normal and the plane wave vector in a cut-plane.This angle determines the shape of the truncated Bessel beam in free space.From Ref.[2],the phase distribution of the metasurface that is used to generate the zero-order Bessel beam atf1can be expressed as[1]

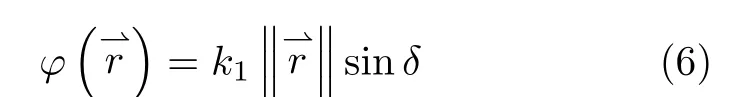
which is illustrated in Fig.2.Hereis the displacement vector between the element and the metasurface center,and thek1is the wave number at the harmonic frequency.The phase distribution is symmetric with respect to the center,which is consistent to the symmetry of the generated beam.

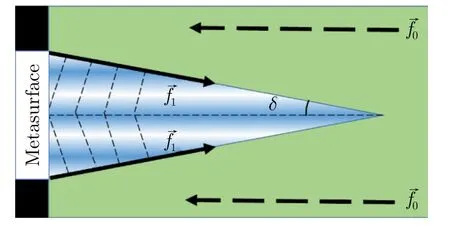
Fig.1 Schematic of the nonlinear Quasi-Bessel beam generation based on the metasurface

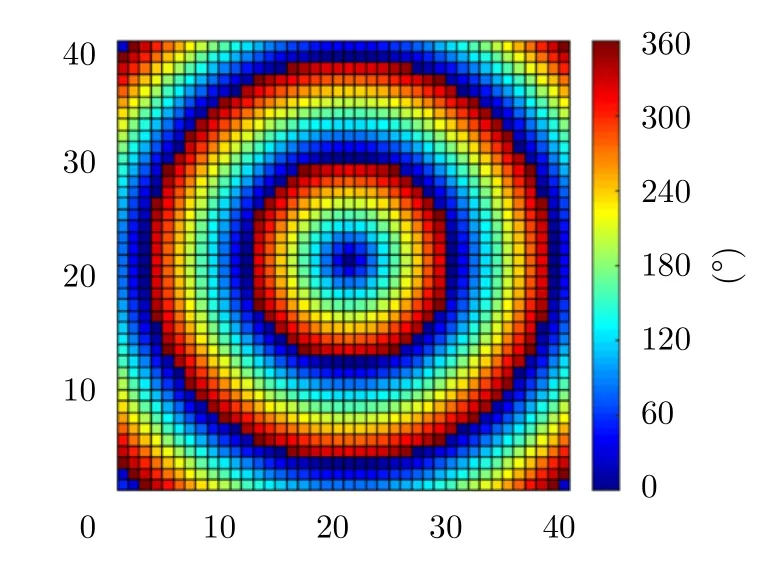
Fig.2 Phase distribution of the metasurface in order to get a nonlinear zeroth-order Quasi-Bessel beam

The relationships betweenβ,kρandk1are described by Eq.(5).According to Eqs.(2—5),the Bessel beam is composed of an infinite number of plane waves.Moreover,the Fig.1 shows a section of a nonlinear Quasi-Bessel beam,Quasi-Bessel beam can be considered as a superposition of plane waves,whose radial components of the wave vector is equal tokρ.

Two crucial problems remain to be solved to produce a nonlinear Quasi-Bessel beam.The first is how to generate the desired harmonic with high efficiency.The other is how to acquire the accurate harmonic phase profile as described in Eq.(6).As discussed in Ref.[18],for a metasurface with time varying reflectivity,the reflected electric fieldEr(t) can be expressed as[18]

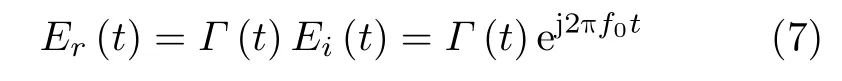
whereEi(t) andEr(t) are the incident and reflected electric fields respectively,andf0is the frequency of the incident wave.Γ(t) is the reflectivity of metasurface.When the incident wave is a monochromatic wave withEi(t)=ej2πf0t,from the Fourier transform the reflected spectrum ofEr(f)can be expressed as

If the reflectivity of metasurface signalΓ(t)is designed as[18]

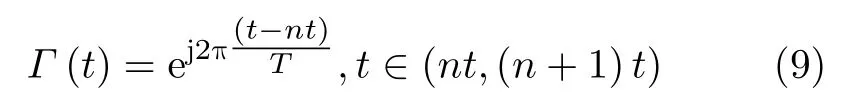
Fig.3 Dependence of the metasurface reflectivity on normalized time (a) and generation of the first order harmonic at the incidence of the monochromatic wave with the carrier frequency of f0(b)

Fig.3(a) shows the phase of the reflectivityΓ(t).The time is normalized by the modulation periodT.It is clear that the phase needs to be changed linearly within each period.It has been revealed that the reflectivity shown in Fig.3 can be used to convert the incident wave into the specified harmonics almost completely because it can effectively suppress higher harmonics[18].

Although from Eq.(9) we are able to obtain a nonlinear harmonic with high efficiency.However,it is hard to control the harmonic phase of the meta-atoms as needed.This problem can be resolved by introducing a small time delayτinΓ(t),

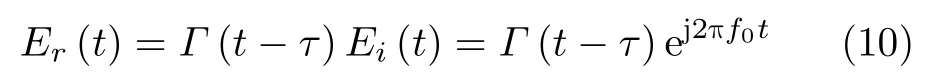
The reflected wave in the frequency domain can be expressed as

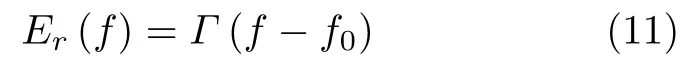
where the frequency of the incident wave isf.The phase shift of the first harmonics caused by time delay is−2πfτ[18].Fig.4 shows the dependence of the first harmonic phase (f=f0) on the time delayτ,where is normalized to the periodT.It shows that a full phase range can be achieved by selecting properτ,leading to the independent control of the harmonic phase required for the generation of Quasi-Bessel beam at nonlinear harmonic frequencies.

Fig.4 Dependence of the first harmonic phase on the delay time(Time delay quantization effects are taken into account)

Based on the aforementioned modulation strategy,we are able to design a time domain digital coding metasurface for nonlinear Quasi-Bessel beam generation.Here the metasurface is designed to operate at 12 GHz.The modulation frequency is set to be 100 MHz which can be generated by FPGA.Therefore the first order harmonic frequency is 12.1 GHz,and the conversion efficiency from the incident wave to the first order harmonic is 100% in theory.

For the digital coding metasurface,the reflection phase is usually discrete intead of continuous when the PIN diodes are used in the element design.The phase discretation leads to small degradation of the conversion efficiency as revealed in[18],which means more harmonics emerges in this case.This is clearly illustrated in Fig.5.

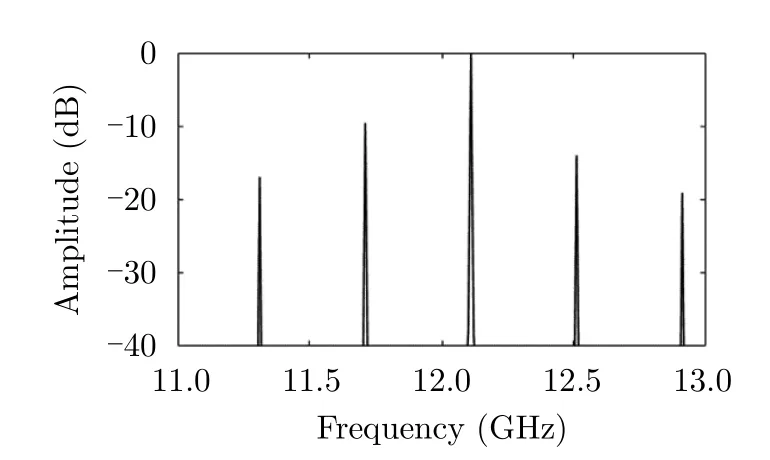
Fig.5 The relative amplitudes of the higher-order harmonics due to the time delay quantization

But the independent amplitude/phase is not affected.In addition,the phase profile of the whole metasurface is also discretized,and its influence on the beam generation needs to be further evaluated.

3 Numerical Results

In general,the Quasi-Bessel beam from the metasurface could be decomposed into a series of plane wave,making it possible to calculate the beam field distributions through numerical simulations.Here the commerical software package MATLAB is used to simulate the generated nonlinear Quasi-Bessel beam through the nonlinear modulation of the metasurface.The metasurface is made of 41×41 elements in all,which are arranged in a rectangular pattern.The period of the element is 10 mm,and the cone angle of Quasi-Bessel beamδ=15°.

From the linear property of Fourier transform,we have

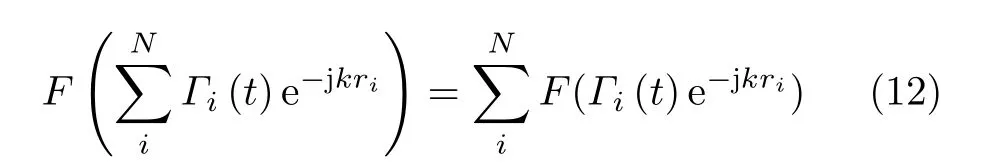
whereFis the Fourier transform operator.Γiis the transient reflectivity on thei-th meta-atom.kis the wave number in free space.riis the distance from thei-th meta-atom to the observation point.From Eq.(12),we can calculate the amplitude and phase of the first harmonic for each element,and then add up all the coefficients to obtain the amplitude and phase of the first harmonic generated from the whole metasurface,as it can help reduce the calculation complexity in the simulation.

The electric fields in front of the metasurface can be obtained after removing the time variable as follows:

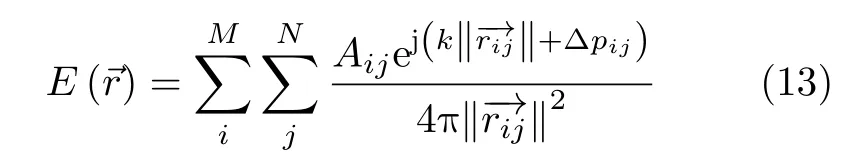
According to Eq.(13),the electric fields in the space can be obtained by discretizing the space and calculating the field at each point.By executing such a numerical simulation,some images of the electric field are attained.

Figs.7(a) and (b) demonstrate the simulated electric field distributions of the first harmonic at a cut-plane perpendicular to the metasurface,corresponding to the cases of continous and discrete phase respectively.By comparing the two figures,we can find that the mainlobes and sidelobes are slightly disturbed by the phase quantization errors,and the focusing ability is kept well as expected.

Fig.8 shows another snapshot of the simulation electric field distributions for the first order harmonic at 12.1 GHz,when the coding metasurface with discrete phase states are employed.It can be seen that the beam is collimated at the center with the intensity larger than that in the rest of the regions.Due to the finite period of the meta-atom,the sidelobes are also obvious around the beam center.However,the influence is quite limited according to the simulation results.

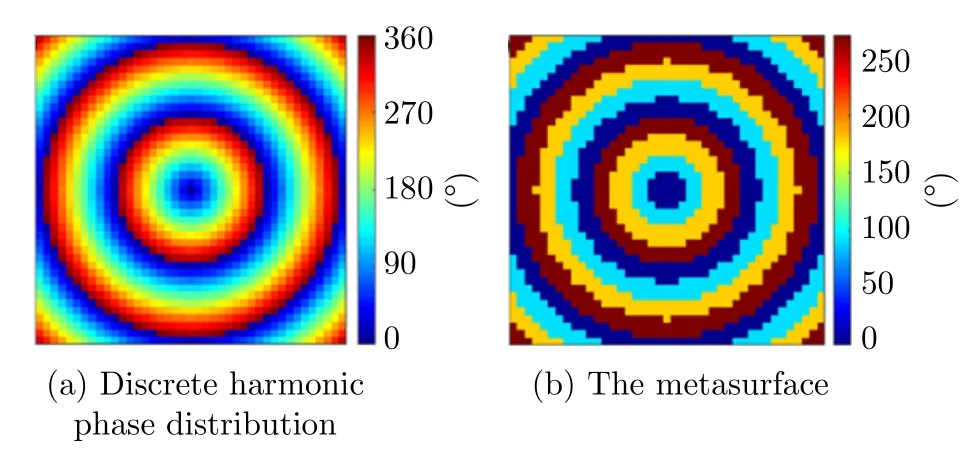
Fig.6 Continuous harmonic phase distribution (a) and discrete harmonic phase distribution (b) of the metasurface

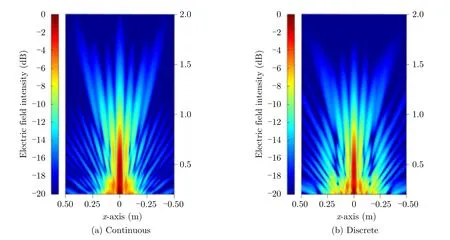
Fig.7 Simulated electric field distributions of the first order harmonic Quasi-Bessel beam at a cutplane perpendicular to the metasurface,when the phase profile of the metasurface

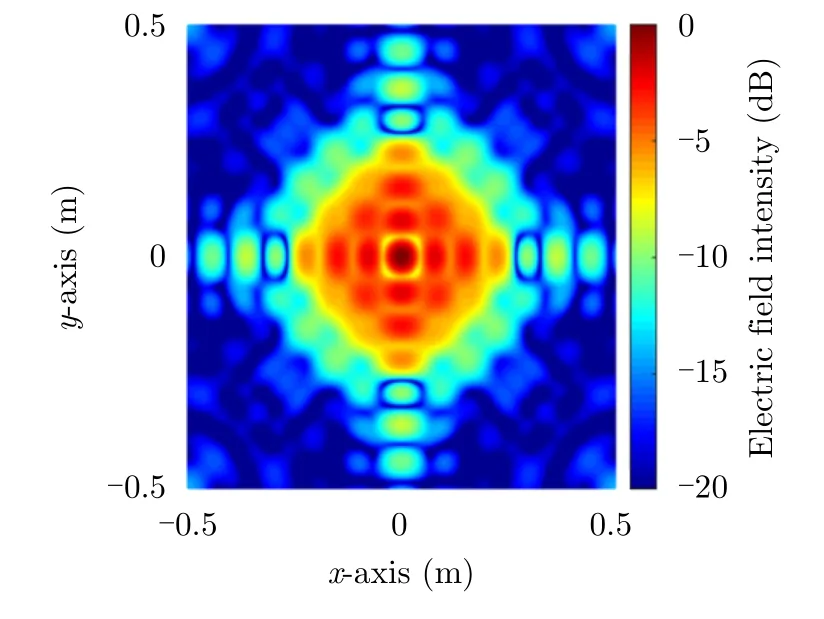
Fig.8 The simulated first order harmonic electric field distributions at a cutplane parallel to the metasurface

4 Conclusion

In this paper,we realize the generation of an nonlinear Quasi-Bessel beam by a time-domain digital coding metasurface.To achieve the required phase profile of the metasurface in order to get a Quasi-Bessel beam at the first harmonic frequency,a periodic reflection coefficient with triangular phase distributions is considered to get a high conversion efficiency from fundamental to the first order harmonic,and a time delay is used to obtain the harmonic phase for each element.Numerical simulations reveal that the nonlinear Quasi-Bessel beam can be generated as expected,and the discrete phase states introduced by the digital coding metasurface have limited impact on the beam properties,which agree well with theoretical predictions.