猪活动区域多孔介质模型及其阻力系数的CFD模拟

刘德钊 辛宜聪 荣 莉 王朝元 李保明

(1.浙江大学 生物系统工程与食品科学学院，杭州 310058；2.奥胡斯大学 土木与建筑学院，丹麦 奥胡斯 8000；3.中国农业大学 水利与土木工程学院，北京 100083;4.农业农村部设施农业装备与信息化重点实验室，杭州 310058)

良好的猪舍内环境对猪健康生长和生产力的提高至关重要。计算流体力学(Computational fluid dynamics, CFD)近年来被广泛用于畜禽舍内气流、温湿度和气体浓度的模拟研究，已成为研究舍内环境的重要手段之一[1-3]。在以往对猪舍内环境的CFD模拟中，为简化计算猪体模型通常被省略[4-5]。然而，在对猪舍进行模拟时，将猪体存在因素考虑在内对准确模拟舍内空气流动非常重要。因此有些研究尝试在舍内环境模拟中建立实际尺寸的猪体模型[6-7]，如Seo等[8]对全尺寸商业猪场中648头猪进行详细建模，采用CFD模拟探究了舍内温度分布和气流模式。然而，在有大量动物的情况下采用这种方式进行建模，普通台式机以及专业的Workstation计算机根本无法满足如此巨大的计算量要求，同时计算时间会成倍增加。

采用多孔介质模型简化动物区域可以有效解决这一难题[9-10]。应用多孔介质模型，需要先获得模型设定所需的阻力系数，即多孔介质区域的入口速度与进出口压降之间的关系。Du等[11]求取养鸡场的笼养鸡区域的阻力系数，将其简化为多孔介质模型，探究养鸡场内气流、温度和相对湿度的分布，结果显示模拟与实测结果吻合良好。Cheng等[12]探究蛋鸡的几何形状、分布以及体重对阻力系数的影响，为将蛋鸡区域简化为多孔介质模型提供了参考。在养猪场中，直接测量养猪区域的风速以及压降存在较大困难，因此通常采用CFD模拟获得不同风速下养猪区域的压降进而计算多孔介质模型所需的阻力系数[13]。然而，猪体的不同几何模型假设对气流产生的阻力存在差异。在此前的研究中，学者们通常会将猪体模型进行简化，省略细小的部位，例如尾巴、耳朵、四肢，在保证模拟准确度的情况下节约计算成本[14]。Li等[15]将省略了细小部位的猪体模型用于对流换热损失的模拟研究，可是在实际畜禽场的模拟中，由于动物的实际尺寸和不规则的形状，省略细小部位的动物简化模型仍然会产生较大的计算量[16]。因此，学者们开始使用简单的几何模型代替动物模型，如圆柱体、椭球体和球体等[17-18]。Mondaca与Choi[16]发现球体、圆柱体和6个圆柱的装配体均能较好的模拟奶牛平均热通量。Li等[19]将实际尺寸的猪模型与圆柱体模型进行对比，结果表明2种模型的对流换热系数具有较强的相关性，可以采用圆柱模型作为猪的简化模型。但是该研究仅考虑了猪在站立时的情况，而在实际养殖过程中育肥猪大约80%的时间都处于躺卧状态[20]，而且目前仍没有研究表明何种简化几何体可代表猪的躺卧模型以及不同几何体简化模型之间阻力系数有何差异性。因此，研究猪在躺卧姿势下对气流的阻碍作用是非常有必要的。

本研究以躺卧的育肥猪作为研究对象，将简化后的猪体躺卧模型作为参考模型，并选择半椭球、椭球、半圆柱3种简单几何体分别代替简化猪模型，计算得到的阻力系数可用于之后的猪舍全尺寸模拟，探究4种模型的阻力系数之间的差异以及对动物区域气流以及压力分布的影响，为多孔介质模型在动物区域的使用和动物模型的简化与选择提供参考。

1 材料与方法

1.1 CFD模拟方法验证

为确保在对不同躺卧猪模型的探究过程中所采用的模拟方法的有效性，参考Cheng等[12]已发表文献中的风洞实测值对本研究的CFD模拟进行验证。Cheng等采用直径为150 mm的球体代替1.5 kg的鸡模型，在长为6 910 mm、宽和高均为500 mm的风洞内进行试验，主要测量了鸡区域内5条垂直测量线(L2～L6)的风速值，再对此风洞试验进行CFD模拟。这与本研究中猪区域以及计算域的气流特性相近，且同样分为X、Y和Z3 个方向分别求取阻力系数。CFD模拟方法的验证采用探究不同躺卧猪模型阻力系数时所用的模拟方法对文献中的风洞试验进行CFD模拟，参考Cheng等的几何模型及边界设置，几何模型如图1所示。采用非结构化四面体网格对计算域进行网格划分，并选择3种数量的网格对验证模拟进行网格独立性检验，高密度网格数量为3 574 326，中等密度网格数量为2 708 984，低密度网格数量为1 769 593，模拟所得到的鸡区域进出口的压降依次分别是0.381、0.383 和0.398 Pa，由于高密度网格与中等密度网格设定下压降的误差仅为-0.52%，因此选择中等密度的网格进行验证模拟。采用标准k-ε湍流模型和scalable壁面函数，压力-速度耦合选用SIMPLE算法，动量、湍动能和湍流耗散率选用二阶迎风离散格式。将本研究CFD模拟得到的风速廓线与文献中的风洞实测值进行对比，计算得到平均相对误差，用于验证本研究模拟方法的有效性，平均相对误差计算公式如下式：

图1 验证几何模型Fig.1 Geometric model of validation

(1)

式中：MRE为平均相对误差；n为测点数；xi为第i个点的速度模拟值，m/s；yi为第i个点的速度测量值，m/s。

1.2 猪躺卧模型的阻力系数

1.2.1猪的躺卧模型

本研究选择55 kg育肥猪作为研究对象，研究表明在猪的所有躺卧姿势中，侧躺且四肢伸展姿势占比高于60%[21]，因此本研究中猪的躺卧模型均基于此种姿势。猪重量与体尺之间的幂函数关系如下[22]：

L=(26.8±0.7)M(0.33±0.01)

(2)

H=(8.7±0.2)M(0.30±0.01)

(3)

W=(7.7±0.2)M(0.37±0.01)

(4)

式中：L为躺卧猪体总长度，cm；H为躺卧猪体高度，cm；W为躺卧猪体宽度，cm；M为猪的体重，kg。

由上述公式计算得到猪主要身体部位的尺寸，结合实际中猪的形状进行简化并建立了躺卧时的简化猪模型。以简化猪模型作为参考模型，将简化猪模型继续简化为3种简单几何模型，分别为半椭球模型、椭球模型和半圆柱模型，根据简化猪模型的体尺建立半椭球模型、椭球模型和半圆柱模型，再对这3种简单几何模型的体尺进行微调使得这3种模型的体积都与简化猪模型的体积相同，如图2所示。考虑到圆柱体放置在地板上时与地板间的空隙较大，不符合猪在躺卧时的实际情况，因此没有选择圆柱体模型。猪的尾巴、耳朵和四肢等部位在划分网格时会显著增加网格数量，而这些部位在猪躺卧的情况下对气流的影响较小，因此在建模时省略。

图2 猪的4种躺卧模型Fig.2 Four geometric models of lying pigs

1.2.2猪的分布

猪的数量和在猪栏内的分布对气流有非常大的影响。模拟所选择的猪场位于浙江省义乌市(29°21′N，119°94′E)，根据此猪场的实际养殖规模以及内部结构，其中单个猪栏长L=5 680 mm、宽W=4 850 mm，猪栏高度根据猪站立时的高度H设置为700 mm[9]。猪栏中实心地板区域和漏缝地板区域分别占猪栏总面积的30.99%和69.01%，共有27头猪。猪的躺卧方向参考猪舍内不同时段拍摄的实际照片得到。根据Bjerg等[9]提出的猪栏内猪的分布规律，实心地板区域应有13头猪躺卧、2头猪站立，漏缝地板区域应有9只猪躺卧、3只猪站立。结合Li等[15]在CFD模拟中采用的猪舍内分布和此研究中实际猪和猪栏的大小，本次模拟的猪的分布以半椭球模型分布为例，如图3所示。本研究的研究对象仅为猪的躺卧模型，因此4种不同躺卧模型下猪的分布完全相同，仅躺卧模型不同，猪栏内共有5头猪站立，均采用简化猪模型，离地277.9 mm。

图3 半椭球躺卧猪模型分布Fig.3 Distribution of half ellipsoid lying pig model

1.2.3计算域与边界条件

计算猪体所在区域X、Y和Z3个方向上的阻力系数的计算域如图4所示。进风口设置为速度入口边界，风速取0.05、0.10、0.15、0.20和0.25 m/s。出风口设置为压力出口边界，猪的表面设置为壁面边界，其余面均设置为对称边界。

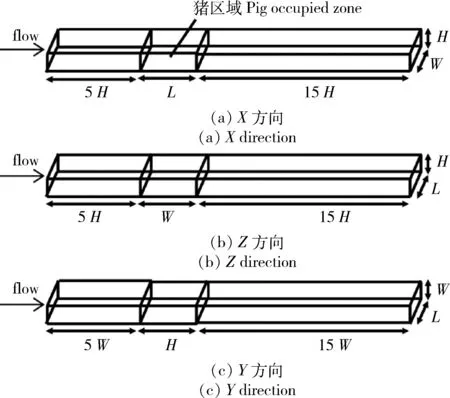
图4 不同方向的计算域Fig.4 Computational domains of different directions

1.2.4网格划分与数值求解

基于CFD验证模拟中网格划分经验对计算域进行网格划分，同样采用非结构化四面体网格。控制方程采用基于有限体积的离散方法，即采用雷诺平均N-S方程(RANS)。同时，本模拟研究采用标准k-ε湍流模型和scalable壁面函数。标准k-ε湍流模型自从被提出之后就变成工程流场计算中主要的湍流模型，scalable壁面函数能避免计算结果恶化，对于任意细化的网格能给出一致的解。此外，求解压力耦合方程的半隐方法(SIMPLE)用于压力-速度场修正，而动量、湍动能和湍流耗散率选用二阶迎风离散格式。

1.2.5阻力系数的计算

CFD模拟通常将动物所在区域简化为多孔介质模型进行求解，能够降低建模以及网格计算的难度。准确的阻力系数对多孔介质模型的设置至关重要，包括黏性阻力系数与惯性阻力系数。有限厚度的多孔介质模型的阻力系数如下式Darcy定律所示[13]：

(5)

式中：Δp为压力降，Pa；1/α为黏性阻力系数，1/m2；C2为惯性阻力系数，1/m；μ为空气动力粘度，Pa/s；ν为风速，m/s；ρ为空气密度，kg/m3；Δn为多孔介质区域厚度，m。

将风速与模拟所得的进出口的压降拟合成常数项为0的一元二次方程，其二次项与一次项前的系数通过式(5)可解得惯性阻力系数与黏性阻力系数。

1.3 多孔介质模型验证

为了能够将躺卧猪模型简化为多孔介质模型，在求解得到阻力系数之后还需要采用多孔介质模型验证其准确性。将养猪区域设置为多孔介质区域并设置阻力系数，其余设置均与躺卧猪模型的阻力系数求解相同，在不同风速下进行CFD模拟，将所得验证压降值与不同躺卧猪模型的模拟压降值进行对比，验证阻力系数的准确性。

2 结果与分析

2.1 CFD模拟方法验证

图5为CFD模拟得到的5条不同测量线(L2～L6)的风速廓线与文献中风洞实测值的对比。从图中可以看出，在大多数情况下模拟值与实测值吻合较好，在L5实测值与模拟值之间的差异性较大，这是因为标准k-ε模型本身不能很好模拟回流区所造成的。本研究中模拟值与实测值的平均相对误差为8.41%，Cheng等采用相同的湍流模型所得误差为8.10%。因此，本研究中采用的模拟方法能够合理地模拟动物区域的气流运动。

图5 不同测量线的模拟风速廓线与实验测量值Fig.5 Simulated velocities profiles and experimental measurements along different measuring lines

2.2 不同几何模型对单位长度压降的影响

图6为简化猪模型、半椭球模型、椭球模型和半圆柱模型在X、Y和Z方向上速度与单位长度压降之间的关系以及拟合方程。由图6可以看出，单位长度的压降随速度的增加而增大，并且在同一方向上，速度越大，4种模型的单位长度压降值相差越大。以简化猪模型作为参考模型，简化猪模型与半椭球模型之间的相对误差在X方向上为-21.6%～-21.2%，在Z方向上为-24.5%～-23.5%，在Y方向上为6.9%～7.0%。简化猪模型与椭球模型之间的相对误差在X方向上为-2.9%～-1.1%，在Z方向上为-11.3%～-9.0%，在Y方向上为14.7%～13.6%。简化猪模型与半圆柱模型之间的相对误差在X方向上为-6.9%～-6.6%，在Z方向上为-11.6%～-10.3%，在Y方向上为30.6%～31.6%。由此可见，在X和Z方向上，简化猪模型与椭球模型的单位长度压降值的相对误差最小，与半椭球模型之间的相对误差最大，这可能是由于半椭球模型底面与地面完全重合，气流沿着模型表面流线型边缘线流动，减少了对空气的阻力作用，导致单位长度的压降值最小。在图6(a)和6(b)中，单位长度的压降值从大到小依次为简化猪模型、椭球模型、半圆柱模型，但是在图6(c)中，半圆柱模型单位长度压降值最大，这可能是因为半圆柱模型在Y方向上的投影面积最大，而投影面积与阻力成正相关，投影面积越大，对气流阻力越大，单位长度压降越大。

图6 4种躺卧猪模型在X、Y和Z方向上速度与单位长度压降之间的关系Fig.6 Relationship between velocity and pressure drop per unit length of four lying pig models in X, Y and Z directions

2.3 不同几何模型对阻力系数的影响

表1为4种模型在不同方向上的惯性阻力系数与黏性阻力系数，由表1可知，在X、Y和Z3种方向上，4种模型均在Y方向上的惯性阻力系数最大，X方向上的惯性阻力系数最小，这可能是因为4种模型在Y方向上的投影均大于X和Z方向，这与Cheng等[12]研究简化鸡模型阻力系数的结果一致。椭球模型与简化猪模型的惯性阻力系数在X和Z2个方向上最为接近，其在X、Z和Y方向上的惯性阻力系数与简化猪模型之间的相对误差分别为-4.0%、-12.2%和14.7%。黏性阻力系数值在表1中无明显规律，且将风速值代入公式(5)中经过计算可知一次项对单位长度压降的贡献较小，因此没有对黏性阻力系数进行详细分析。根据阻力系数可知，椭球模型与简化猪模型最相似，因此在今后对多孔介质模型的应用研究中，为了降低建模的难度，可以使用椭球模型代替简化猪模型对阻力系数进行求解，并且为今后利用多孔介质模型模拟全尺寸猪舍的CFD研究提供了可靠的数据。本研究中所得阻力系数的结果是在假设猪的体重为55 kg的情况下计算得到的，并不能代表猪在其他体重下的阻力系数，在后续的研究中将会对不同体重下猪体模型的阻力系数进行系统性的研究。

2.4 不同几何模型对气流分布的影响

图7为不同几何模型在X方向上，风速为0.25 m/s 时猪栏内y=160 mm平面上的风速分布，由图中可以看出，不同猪体模型会影响风速的分布。简化猪模型、半椭球模型、椭球模型和半圆柱模型在此平面的最大风速分别为0.42、0.46、0.44 和0.45 m/s，结合图中可知，半椭球与半圆柱对风速分布影响较为明显，模型背风面低风速区域与高风速区域明显多于其他2种模型，这可能是因为半圆柱与半椭球模型底面与猪栏地板重合，对气流完全阻挡，造成背风面处风速更低，其在X方向上惯性阻力系数较低，因此高风速区域也相对较多。椭球模型与简化猪模型对气流影响最相似，与表1中阻力系数结果一致。然而在Cheng等[12]的研究中，通过分析鸡模型与椭球模型的风速分布图，最大风速分别为5.78 和4.30 m/s，得出椭球模型不能代替鸡模型的结论，这可能是因为鸡模型相对于椭球模型来说更为复杂，且椭球模型将鸡的脖子以上部分全部省略，导致2种模型相差较大，并且鸡在鸡笼中的分布更为紧密，孔隙率低，因此模型的不同会导致在风速分布上的显著差异。而对于本研究，躺卧时猪的体态相比鸡更为圆润，猪在躺卧时的高度仅约为站立时的一半，因此上方空间更大，所以椭球模型与猪模型对气流分布的影响并无显著差异。此外，Li等[23]采用CFD探究鸡的对流换热系数，结果表明，球体模型与鸡模型的对流换热系数拟合较好，在后续研究中可以采用球体模型代替鸡模型。因此，在简化模型时需要根据不同动物的特征以及在舍内的分布情况进行简化，同时模型的简化程度也受到研究目的的影响。

表1 4种躺卧猪模型在X、Y和Z方向上的阻力系数Table 1 Resistant coefficients of four lying pig models in X, Y and Z directions

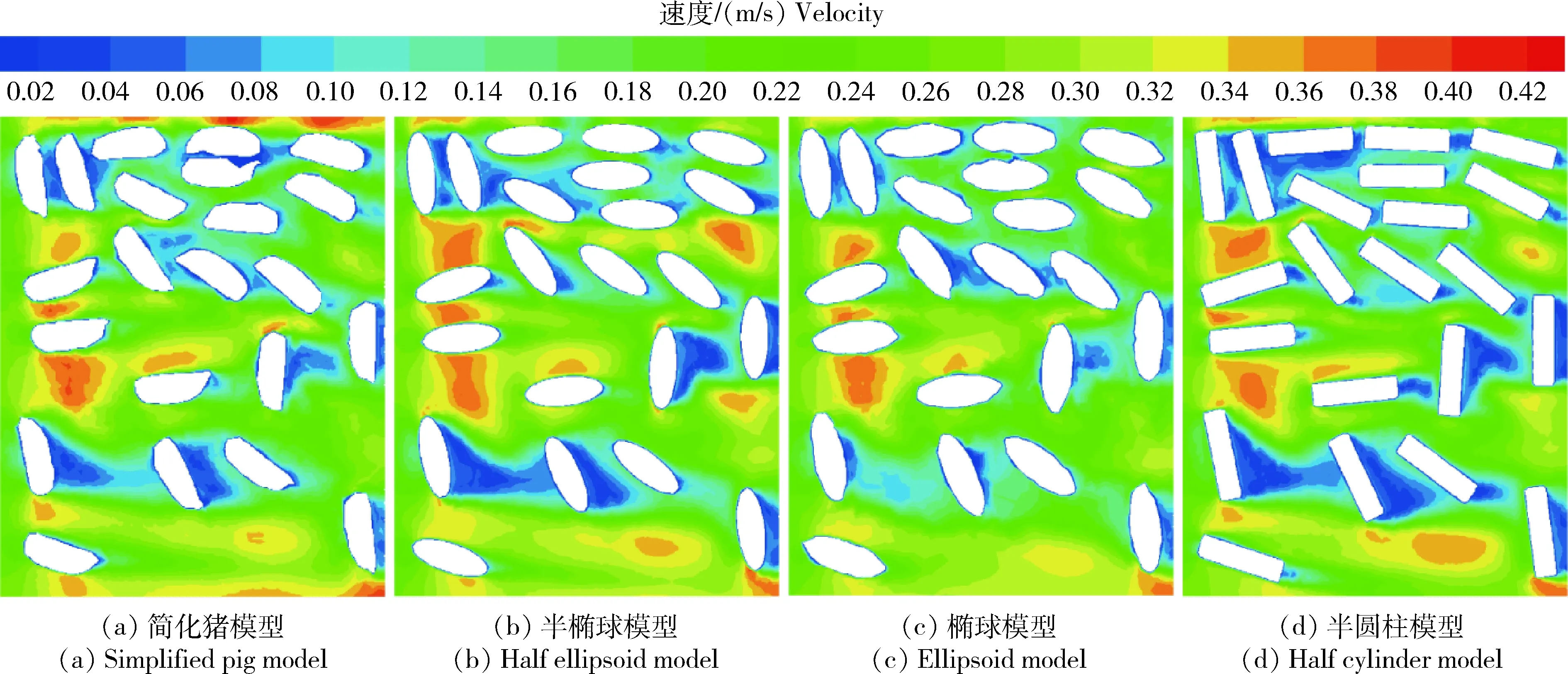
图7 4种躺卧猪模型在y=160 mm平面上的风速分布Fig.7 Velocity distribution of four lying pig models in the plane of y=160 mm

2.5 不同几何模型对压力分布的影响

图8为不同几何模型在X方向上，风速为 0.25 m/s 时猪栏内y=160 mm平面上的压力分布。因为4种猪模型的分布完全相同，所以压力分布的变化趋势相同，但是局部压力值存在差异。简化猪模型、半椭球模型、椭球模型和半圆柱模型在此平面上的最大压力分别为0.086、0.068、0.097 和0.081 Pa。从图中可以看出，猪模型的存在使得在猪的身后产生了气流分离与低压区，较大的压力值均出现在靠近进风口的猪模型的迎风面，而在远离进风口的位置处则出现负压。在猪分布密集区域，4种模型的压力分布差异不明显，而在猪模型分布稀疏的区域，模型迎风面产生的较大压力值差异显著。这与Bustos-Vanegas等[24]采用多孔介质模型模拟奶牛区域的空气流动的研究中得到的压力分布规律一致，并且提出虽然动物模型与多孔介质模型得到的局部压力相差较大，但是总压降是相同的，说明多孔介质模型仍是适用的。

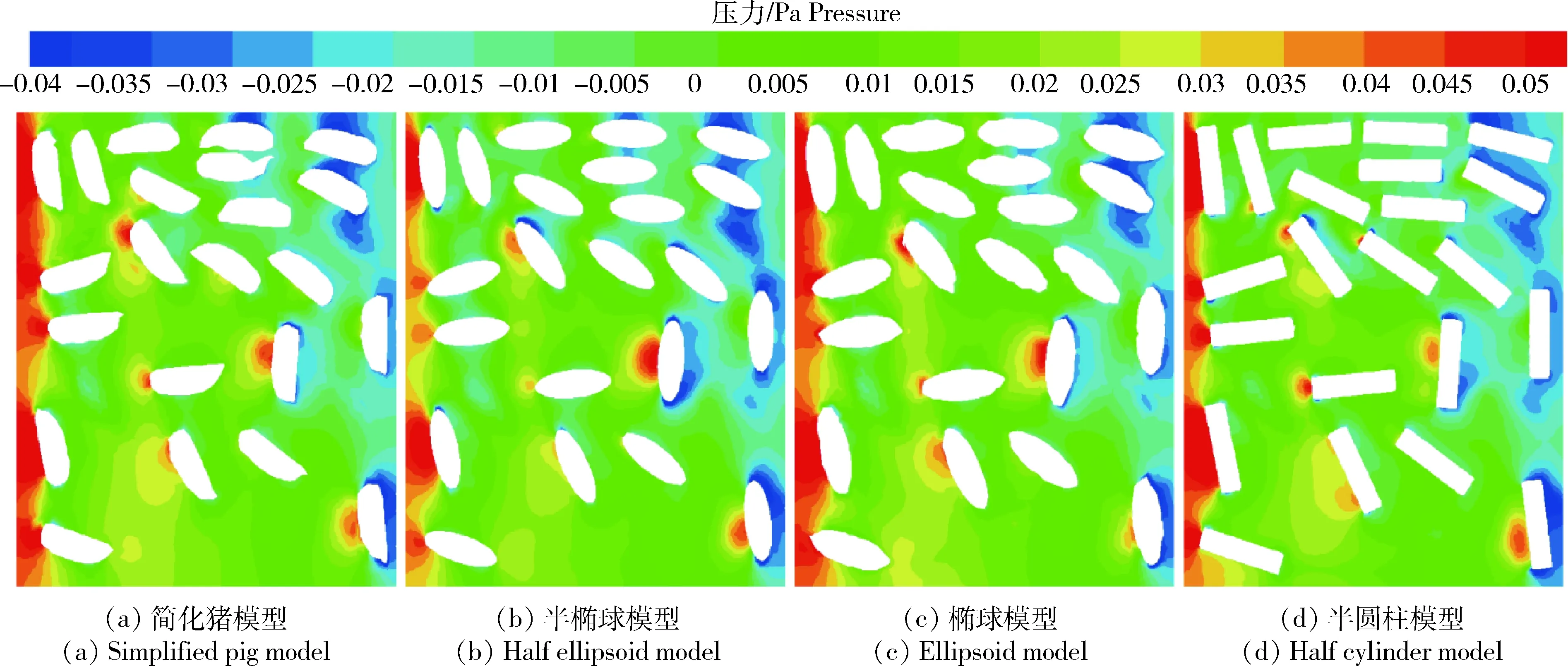
图8 4种躺卧猪模型在y=160 mm平面上的压力分布Fig.8 Pressure distribution of four lying pig models in the plane of y=160 mm

2.6 多孔介质模型验证

图9为简化猪模型在X、Y和Z方向上的模拟压降值与多孔介质模型压降值的对比。由图可知，简化猪模型的单位长度压降值与采用简化猪模型阻力系数的多孔介质模型的单位长度压降值吻合度高。以简化猪模型为例，可以说明采用CFD模拟的方法求解阻力系数是有效的，同时验证了阻力系数的正确性。在之后的研究中可以直接采用多孔介质模型代替复杂的动物模型。

图9 X、Y和Z方向上简化猪模型的多孔介质模型验证Fig.9 Validation of porous media model for simplified pig model in X, Y and Z directions

3 结 论

本研究对简化猪模型、半椭球模型、椭球模型和半圆柱模型4种躺卧猪模型进行了CFD模拟，探究了不同躺卧猪模型对阻力系数的影响。得出以下结论：

1)采用本研究的CFD模拟方法得到的风速值与文献中的风速实测值吻合较好，平均相对误差为8.41%。

2)简化猪模型与椭球模型单位长度压降之间的相对误差在X方向上为-2.2%～-1.1%，在Z方向上为-11.3%～-9.0%，在Y方向上为14.7%～13.6%。在X、Z和Y方向上的惯性阻力系数相对误差分别为-4.0%、-12.2%和14.7%，在今后的研究中可以使用椭球模型代替简化猪模型。

3)不同躺卧猪模型会影响猪栏内风速和压力的分布。椭球模型与简化猪模型栏内的气流分布基本一致，半椭球与半圆柱模型则对气流分布产生了显著影响。压力分布的差异主要体现在躺卧猪模型分布稀疏的区域。

4)将通过躺卧猪模型求解得到的阻力系数用于多孔介质模型，能够得到与模拟单位长度压降值吻合度较高的验证值，说明多孔介质模型对于简化动物区域是适用的。