基于PCA的土壤Cd含量高光谱反演模型对比研究

郭 飞，许 镇，马宏宏，刘秀金，杨 峥，唐世琪

1.中国地质科学院地球物理地球化学勘查研究所，河北 廊坊 065000 2.中国地质调查局土地质量地球化学调查评价研究中心，河北 廊坊 065000 3.中国科学院空天信息创新研究院，北京 100101

引 言

镉(Cadmium，Cd)是一种有毒重金属[1]，它不仅会降低土壤微生物的生物活性，还易通过在植物可食部位的累积，进入食物链危害人体[2]。矿产资源的开采是造成其周边农用地土壤污染的重要原因之一[3]。如何快速有效测定土壤中Cd的含量及空间分布已成为目前亟待解决的问题。高光谱遥感由于光谱分辨率高、波段连续，能快速高效获取精细的光谱信息等优势，成为快速查明土壤重金属污染状况的新技术方法之一[4]。

利用可见-近红外光谱对土壤重金属含量进行定量反演已成为国内外热点研究问题。Kemper等[5]利用可见-近红外光谱，基于线性模型MLR建模预测As和Cd等重金属含量，认为土壤重金属含量与铁、铁氧化物相关；有研究采用SMLR，PLSR等线性建模方法建立了土壤重金属含量反演模型；有报道基于逐步回归和相关系数方法，筛选出对重金属敏感的特征波段，将它们组合成综合特征变量对研究区Cu元素进行了反演。尽管国内外关于土壤重金属含量估算相关研究逐渐增多，但是仍存在一些问题。例如，针对高光谱数据波段信息冗余的问题，多数研究选择丢掉大量的波段，仅利用相关系数以及逐步回归法筛选出了部分特征波段，损失了大量有用的信息。事实上，土壤中重金属含量与光谱曲线之间的关系很难用几个波段解释。因此，选择一种既可以保证波段主要信息量，又能减少输入变量的特征参数尤为重要。此外，关于土壤重金属含量估算模型的问题，绝大部分的研究主要采用线性回归模型，如SMLR和PLSR等；而非线性回归模型考虑较少。客观上讲，土壤中重金属含量在光谱曲线上的响应会受多种因素影响，二者之间关系非常复杂；而简单线性回归模型很难处理非线性、随机性等复杂的问题。因此，在高光谱模型的选择上应对非线性模型加以考虑。

选择湖北省黄石市矿山周边农用地土壤为研究对象，针对于高光谱反演中波段信息冗余等问题，提出了基于PCA的降维方法，结合多种高光谱反演模型，验证PCA筛选主成分量可实现土壤重金属含量的高精度反演，并通过不同高光谱模型的对比，确定了适合该研究区域Cd含量的最佳预测模型，从而实现了土壤Cd含量的快速、精确光谱检测，为土壤重金属反演提供新的思路。

1 实验部分

1.1 研究区与土壤采样

研究区位于湖北省东南部的黄石市(114°30′—115°30′E，29°30′—30°20′N)，地处长江中下游，具有典型的大陆性季风气候。地势南高北低，东西平，海拔高度为120～200 m。研究区内矿产资源丰富，有多个大中型矿床，矿山开采、冶炼生产对周边土壤造成一定的重金属污染。在研究区共采集0～20 cm表层土壤56件，采样点(图1)位于矿山周边的农用地，采集表层土样初始质量大于1 kg，样品经室内自然风干、研磨后过10目(孔径2 mm)的尼龙筛，利用四分法分成两份，分别用于室内光谱测试和实验室化学分析。

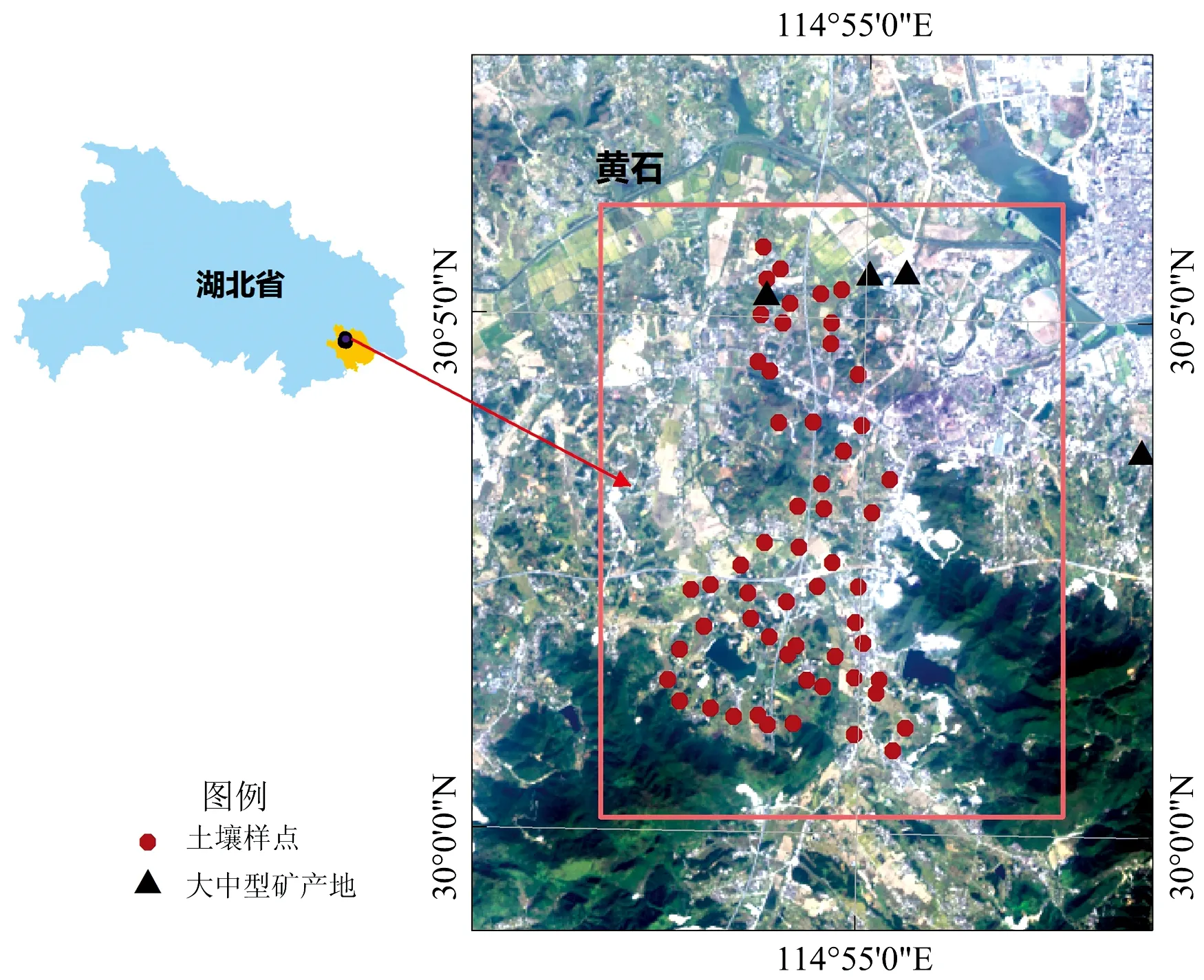
图1 研究区采样点分布示意图Fig.1 The distribution of sampling point in the study area

1.2 光谱测定

土壤光谱数据获取采用美国ASD公司的FieldSpec4地物光谱仪(光谱波段范围350～2 500 nm)，利用卤素光源和标准白板完成测量。该光谱仪采样间隔为1.4 nm(350～1 000 nm)和2 nm(1 000～2 500 nm)，经光谱重采样后(间隔1 nm)，共输出2 151个波段。测试在暗室进行，选择一稳固平台，将土样放入直径90 mm，高19 mm的透明玻璃器皿，使其表面尽量平整，以50 W的卤素灯为光源，光源与样品保持50 cm距离，光源探头位于样本正上方7 cm高，光线与样品保持15°的照射角度，保证测量时无阴影遮挡。开机预热30 min后对仪器进行调整和校准并开始测量。每个土壤样本采集10条光谱曲线，取光谱反射率的平均值作为样本的反射率光谱值，剔除350～399和2 450～2 500 nm信噪比低、噪声大的边缘波段，共获得2 050个波段数据。

1.3 数据处理

1.3.1 光谱预处理

土壤样品光谱数据测定过程中，由于光线亮度变化和土壤表面凹凸不平会对实验结果产生影响，采用取光谱反射率倒数对数的方法来避免此影响。倒数对数[6]计算公式为

(1)

其中λi为光谱波长值，R(λi)为对应光谱波段的反射率。

主成分分析(principal components analysis，PCA)是由Pearson于1901年提出的一种分析、简化数据集的方法[7]。该方法的优势在于降低数据集维数，同时保证信息量最大，对于拥有大量波段信息的高光谱数据，通过一系列的矩阵变化，在测量空间寻找几组正交向量，保留数据方差最大、信息量最多的组分，从而达到高光谱数据降维的目的。主要步骤如下：

(1)将波段数据组合成为矩阵，设随机变量X1，X2，…，XP；其样本均数为X1，X2，…，XP；样本标准差记为S1，S2，…，SP。首先进行标准化变换

(2)

以此类推求得第三，第四，…，第p个主成分。保留主成分个数取决于累积方差在总方差所占百分比(贡献率)。

1.3.2 反演模型

利用PCA对原始光谱以及倒数对数光谱进行波段降维，将累积贡献率达到99.99%的主成分作为特征变量，选择线性模型PLSR，以及非线性模型SVM，ANN和RF分别建立土壤Cd含量估算模型。PLSR是一种常用于高光谱反演土壤元素含量的新型多元统计方法[8]，它能够很好地解决自变量间多重共线问题。SVM是以内核统计学理论为基础理论，它的优势主要体现在解决小样本、非线性以及高维模式的识别[9]。ANN由一组相互连接的人工神经元组成，利用大量神经元之间的链接结构进行分布式并行信息处理的数学模型，该模型基本架构由输入层、输出层和隐藏层三部分构成[10]。RF是一个组合分类器算法[11]，由一系列决策树组成，利用自助法重采样技术，在初始样本数据集上生成多个自助样本集，每个自助样本集是每棵分类树的全部训练数据，然后根据自主样本集生成多个分类树组成随机森林。

1.3.3 精度评估

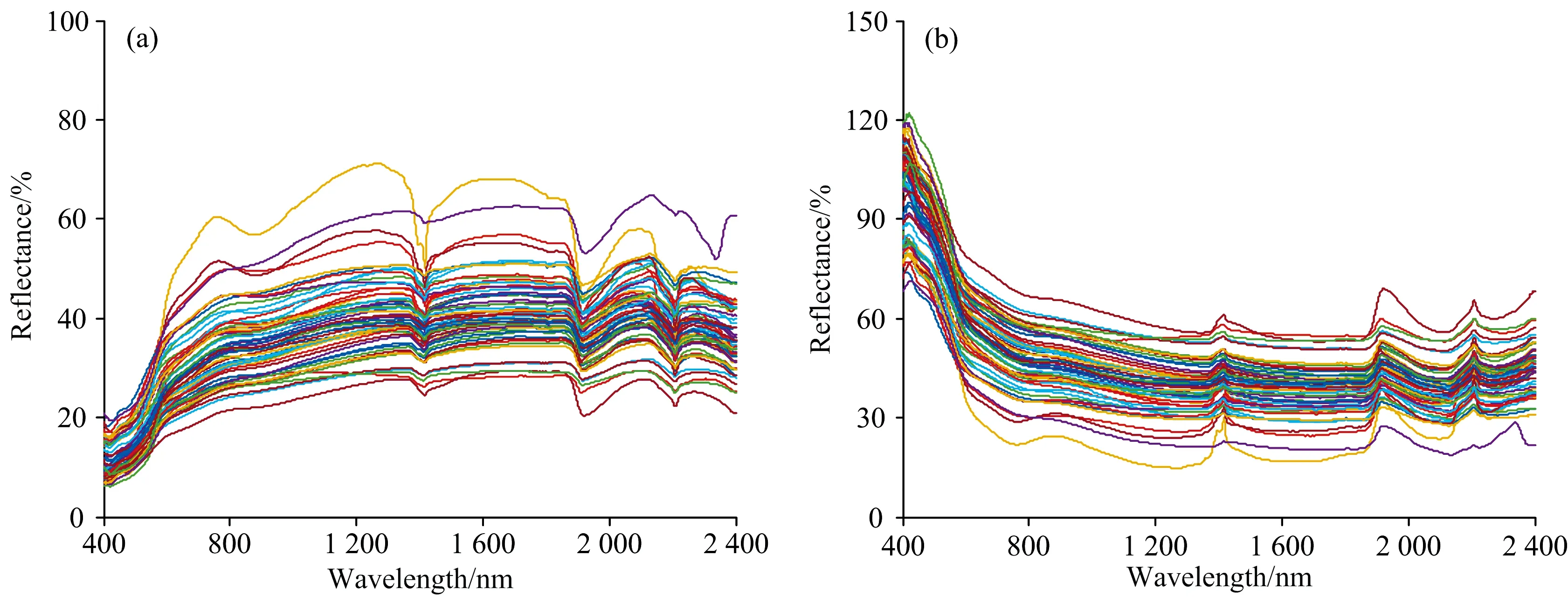
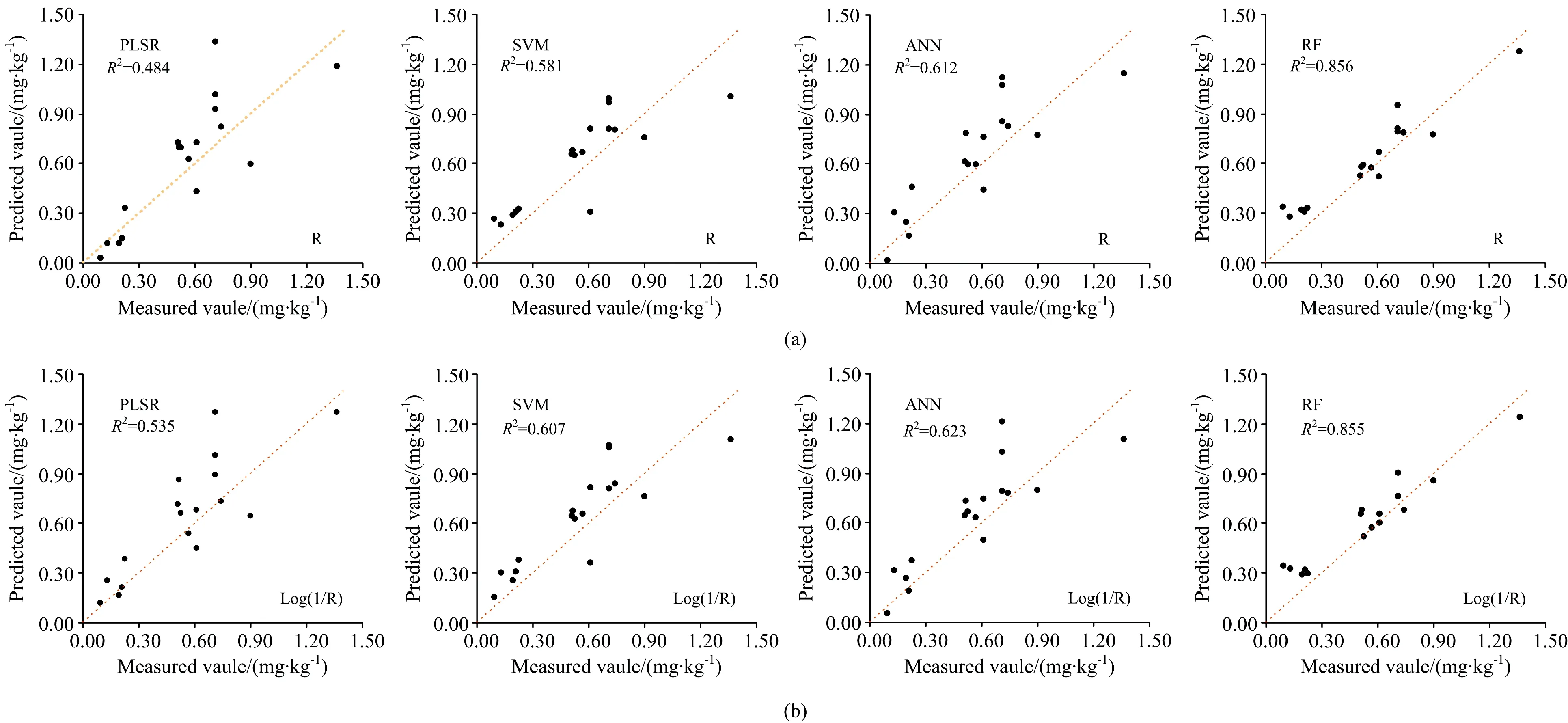
采用R2、RMSE和RPD评价指标对估算模型的反演精度进行评估。R2和RPD越大，RMSE越小，说明预测效果越好，通常认为R2越趋近于1，模型的预测效果越佳。当RPD>2时，模型具极好的预测能力；当1.4

2 结果与讨论

2.1 土壤重金属含量统计分析

利用等离子体质谱法测定Cd含量，Cd元素的描述性统计结果如表1所示，Cd均值为0.64 mg·kg-1。根据土壤环境质量标准(GB15618—2018)，该区域的Cd含量高于农用地污染风险筛选值，而低于管制值，存在一定的土壤污染风险。从空间分布看，其变异系数介于0.5～0.75之间，属于中等变异，说明Cd在土壤中分布不均，空间变异较为显著。将56个样本数据按照7∶3比率随机分割，训练样本39个，用于筛选模型输入变量。验证样本17个，用于对高光谱模型的评估。

表1 土壤Cd含量描述统计分析(mg·kg-1)Table 1 Descriptive statistics analysis of soil Cd content

2.2 光谱变换与PCA降维

所有土壤样本原始光谱反射率曲线[图2(a)]趋势大致相同，在可见光区域反射率呈明显上升，超过800 nm后光谱曲线趋于平缓。在1 400，1 900和2 200 nm附近有三个明显凹陷的吸收峰，为土壤黏土矿物的吸收特征。经倒数对数变化后[图2(b)]的光谱曲线与原始曲线的变化趋势基本相反。

图2 (a)土壤样本原始光谱反射率曲线；(b)土壤样本倒数对数光谱反射率曲线Fig.2 (a) The original spectral reflectance curve of soil samples； (b) The reciprocal logarithmic spectral reflectance curve of soil samples

利用PCA算法，对原始光谱曲线以及变换后的倒数对数光谱曲线的2 050个波段进行降维，原始光谱曲线和倒数对数光谱曲线各主成分的贡献率和累计贡献率值如表2所示。选取经PCA之后，累计贡献率达到99.99%的主成分个数作为模型的输入变量，其中，原始光谱累积贡献率达到99.99%的主成分个数为12个，光谱变换之后累积贡献率达到99.99%的主成分个数也为12个。将PCA降维选取的组分作为四种模型的输入变量。

表2 主成分贡献率Table 2 Principal component contribution rate

2.3 土壤重金属含量反演模型建立与检验

将PCA降维选取的主成分作为模型的自变量(X)，土壤Cd含量为因变量(Y)，采用线性回归PLSR模型，以及非线性回归SVM，ANN和RF模型分别建模比对，验证基于PCA筛选的特征变量对不同模型预测能力的影响，以及优选出研究区Cd含量的最佳预测模型。

2.3.1 基于PCA原始光谱建模

利用PCA对原始光谱数据降维，选择累计贡献率达99.99%的12个主成分量作为模型输入变量，运用PLSR，SVM，ANN和RF方法建模，土壤Cd含量的反演模型[图3(a)]的精度评价如表3所示，根据图3(a)与表3可知：PCA-RF的决定系数(R2=0.856)最高，RPD高达3.39，表明PCA-RF模型具有极好的预测能力，是预测土壤Cd含量的优势模型；PCA-ANN和PCA-SVM的RPD都高于2，其决定系数(R2)分别为0.621和0.581，两种模型同样具有好的预测能力；而PCA-PLSR的R2和RPD分别仅为0.484和1.8，该模型的预测能力一般。经PCA降维选取的特征波段，使得模型均具有一定的预测能力。

2.3.2 基于PCA倒数对数光谱建模

运用四种方法对PCA降维后的倒数对数光谱进行建模[图3(b)]，其反演精度如表3。由图3(b)和表3可知：PCA-RF模型的预测能力在光谱变换后仍为最佳，其R2为0.855，RPD为3.39，表明模型仍具有极好的预测能力；PCA-ANN次之，其R2为0.623，RPD为2.12，模型同样具有好的预测能力；PCA-SVM的R2为0.607，RPD为2.00，模型也具有好的预测能力，而PCA-PLSR的R2为0.535，RPD仅为1.89，模型预测能力一般。

表3 基于原始光谱-倒数对数光谱不同模型精度评价Table 3 Accuracy evaluation of different models based on original spectral-reciprocal logarithmic spectral

图3 (a) 原始光谱不同预测模型散点图；(b) 倒数对数光谱不同预测模型散点图Fig.3 (a) Scatterplots of different prediction models based on original spectral data； (b) Scatter plots between different prediction models based on reciprocal logarithmic spectral

2.3.3 基于PCA原始光谱-倒数对数模型对比分析

四种模型的预测能力顺序在光谱变换前后未发生改变(图4)，光谱变换对于各模型的预测能力有所提升，其中提升效果最为显著的是PCA-PLSR模型，该模型的R2提升了10.5%，RPD提升了5.0%，其次为PCA-SVM模型，该模型的R2提升了4.5%，RPD提升了2.5%，PCA-ANN模型，R2和RPD分别提升了1.8%和1.4%，而PCA-RF模型无明显改变。

图4 原始光谱-倒数对数对比分析图Fig.4 The contrast analysis diagram between original spectral and reciprocal logarithmic

通过对比光谱变化前后各模型的预测精度可得，非线性模型的预测能力优于线性模型，倒数对数光谱变换对于模型的预测能力有所提升，可弱化光谱数据测定时光线亮度和土壤表面凹凸产生影响。

3 结 论

以湖北省黄石市矿区周边农用地土壤为研究对象，利用PCA方法对光谱变化前后数据进行降维，选取特征变量，在此基础上对比分析了不同反演模型对土壤Cd含量测定的反演精度，得出如下结论：

(1)经倒数对数变换后的光谱，预测能力有所提升，PCA-PLSR模型的提升效果最为明显，PCA-SVM和PCA-ANN稍有提高，倒数对数变换可弱化光谱测定中光强度变化和土壤表面凹凸的影响。

(2)利用PCA方法进行降维处理可以有效降低高光谱数据量，选取的12个主成分量对变化前后的光谱累计贡献率可达99.99%，四种模型均具有一定的预测能力，保证模型具有极好的输入变量。

(3)不同模型的反演精度顺序为：PCA-RF>PCA-ANN>PCA-SVM>PCA-PLSR，非线性模型PCA-RF，PCA-ANN和PCA-SVM的RPD均大于2，具有极好的预测能力，其中PCA-RF模型的RPD超过3，说明模型具有较高稳定性和预测精度。

本研究主要采用PCA对光谱数据进行降维，对比分析不同模型的反演能力，PCA-RF模型可为土壤重金属含量反演提供很好的参考依据。PCA对高光谱数据特征变量选取具有显著效果，但仍存在其他的降维方法，需要进一步深入研究。