单边加载下的深基坑水平位移分析

杨永波

(重庆市勘测院，重庆 401121)

1 引 言

深基坑工程施工过程中，根据基坑周边施工环境和设备的安置，可以将基坑各边的荷载类型分为无加载、单边加载和多边加载等几种情况。对于单边加载来说，又可以根据加载的宽度进行分类，主要有基坑边全部加载、基坑边局部加载两种形式[1]。大部分深基础施工时，基坑边处于无加载情况，但在某些施工阶段，由于现场需求，会出现单边施加荷载的状态。这种情况下，有必要进行单边加载状态下的基坑边水平位移分析，以便对风险点有较好的掌握和预判。

桩锚支护体系下的深基坑在施工开始前，需要收集钻勘资料和桩锚支护体系设计资料，结合施工方案进行基坑边水平位移分析[2]。目前的分析手段有基于极限平衡法、有限元法、弹性地基梁法等方法，其中从有限元法发展出来的有限差分法，在工程中应用较多[3]。该方法可以对岩石、土壤、刚体等多种物质的三维受力和变形状态进行模拟，分析其塑性流动情况。它将研究对象分解为微小单元，每一个微小单元作为一个质点，计算和记录质点不同状态下的变化轨迹、变化速率、承受压力等。采用拉格朗日法按照确定的时间步长执行计算程序，从而模拟出这些质点的集合变化、屈服、崩塌过程。

2 基于有限差分的模拟计算方法

2.1 构建分析模型

进行模拟分析，首先要构建分析模型。对桩锚支护结构的深基坑工程来说，有限差分模型主要有土体本构模型、结构单元等[4，5]。土体本构模型较为复杂，工程应用通常进行简化，常用非线性E-B模型、渐进单屈服面模型、Drucker-Prager模型、Null模型和Mohr-Coulombr模型等。基坑工程中的支护体系的结构单元一般包括锚索、梁和桩三种，每个单元的自由度不同，索能受拉和受压，但不能承受弯矩，梁结构适合模拟横向剪切变形以及轴向截面的扭曲变形非常小的构件，桩结构具有索和梁的综合特性。

建立模型需要开展的工作包括选择模型范围、确定模型参数、确定边界条件和初始条件[6]。范围的选择主要由工程施工范围(含影响范围)，限定范围后需要确定差分格网，并定义坐标系。在确定土体模型后，需要输入支护材料的参数，即锚、桩的模拟单元。模型的边界条件包括位移边界条件和应力边界条件，其确定原则为：在模型内部的对称面上，施加位移边界条件，那么该模型在这个方向上的位移矢量和即为零；在外部表面上，对研究模型施加应力边界条件。

2.2 有限差分法模拟步骤

采用有限差分进行计算和分析有以下几个步骤：①由初始节点的速度，推导出节点的应变速率、应变增量和旋转速率三个重要参数；②列本构方程，先后求解单元应力的增量和新单元应力；③获取节点质量、不平衡力以及阻尼力等，求解新的节点速度；④列出节点运动方程[6，7]。基于有限差分的计算是循环模式的，如图1所示：

其模拟流程如图2所示。

图1 基于有限差分的计算流程循环图

图2 有限差分法的模拟流程

3 单边超载的基坑顶部位移案例分析

3.1 工程概况

某高层住宅施工时，需开挖一深基坑，该基坑东西开挖长度为 67 m，南北开挖长度为 31 m，实际开挖深度为自地坪至主楼基础垫层底，约 9 m。该项目场地属于河流冲积阶地，地形平坦。地层自上而下依次排列为人工填土、粉质黏土、含黏性土卵石、粉质黏土、细砂、粉质黏土、泥质粉砂岩。工程地质参数表如表1所示。本项目深基坑支护采用的是人工挖孔灌注桩，并加锚杆。支护桩直径为 1.0 m～1.2 m，长 10.5 m，间距 1.5 m～2.0 m，锚杆布置在距桩顶 2.5 m处。

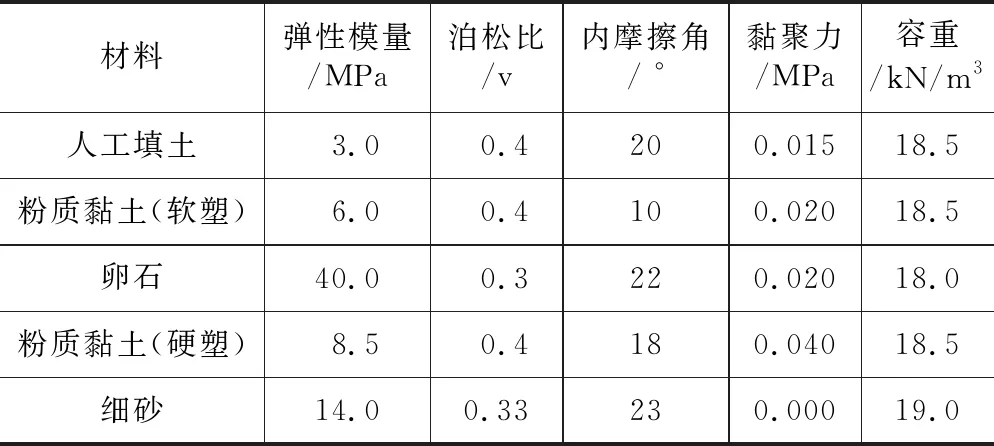
工程地质参数表 表1

本项目按平均间距6 m布设了水平位移监测点，角点处、周边重要设施较近处等位置进行了加密[8]。监测数据显示：基坑顶部监测点的最大水平位移为 15.2 mm，该点位设置在长边中部附近的桩位上。

3.2 无加载情况下变形模拟

在变形监测工作开展的同时，该项目采用有限差分法进行了变形模拟。主要开展工作内容如下：

(1)有限差分程序计算参数

包括本项目的土体参数、支护桩单元参数、支护锚杆参数等，均需输入计算程序。限于篇幅，具体参数本文不再列举。

(2)模拟尺寸及坐标轴定义

为方便研究，对于基坑的水平及竖向以实际开挖值的3倍，作为模拟计算范围，建立的模拟坐标系如图3所示。

图3 模型坐标系建立

(3)施工工况模拟

按照施工工序，将整个计算过程分为赋予土体属性、计算初始地应力、土体在自重条件下达到平衡、模拟混凝土桩打入过程、赋予桩属性、开挖与超挖数值、施加锚杆且赋予锚杆属性、重复开挖和施加锚杆的过程、开挖至基底设计标高等，最后计算结果分析，与实际监测结果对比[9，10]。其中基坑长边模拟计算结果如图4所示：

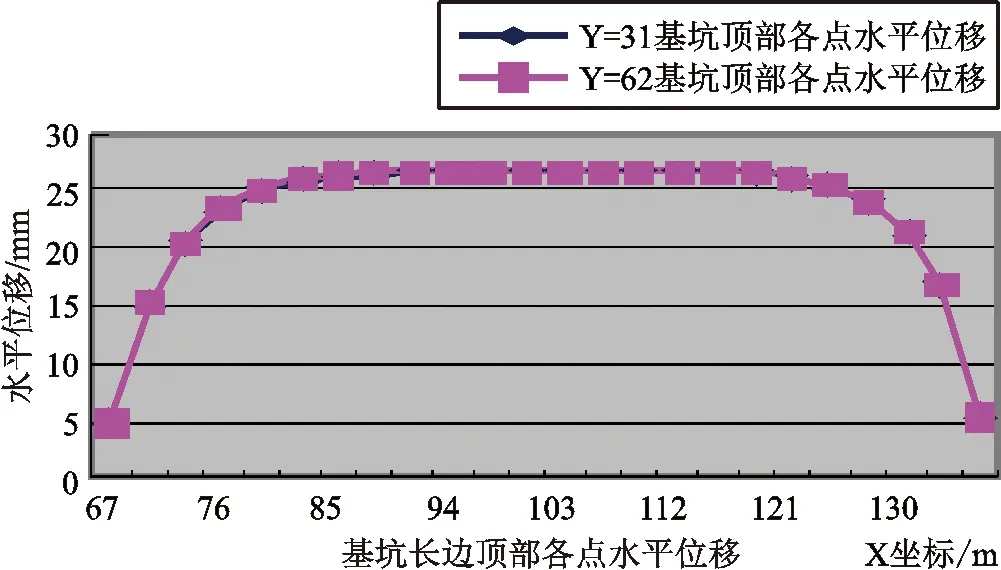
图4 基坑长边顶部各点模拟计算水平位移图

模拟计算与实际监测结果对比情况如下：无加载时，模拟计算所得位移最大的桩位与监测所对应桩的水平位移与实际监测值(15.2 mm)相差 5.1 mm，计算及实际监测的最大位移桩位均位于基坑长边中部。基坑长边土体最大水平位移为 26.65 mm，短边土体最大位移为 25.66 mm，均位于基坑边的中部，土体的位移值均为模拟计算值，无实际监测值进行对比。

3.3 单边施加满载情况下变形模拟

以短边加载为例，对整个短边加载，加载大小为 20 kPa(表2)。

对整个短边满荷载的模拟工况 表2

将该工况下模拟计算值与无加载情况下的基坑模拟计算值进行对比。由于数据量较大，而本次模拟只是将荷载加载于两条短边的其中之一上(加载短边为X=134的短边，即基坑右侧的短边)，对比情况如表3所示。

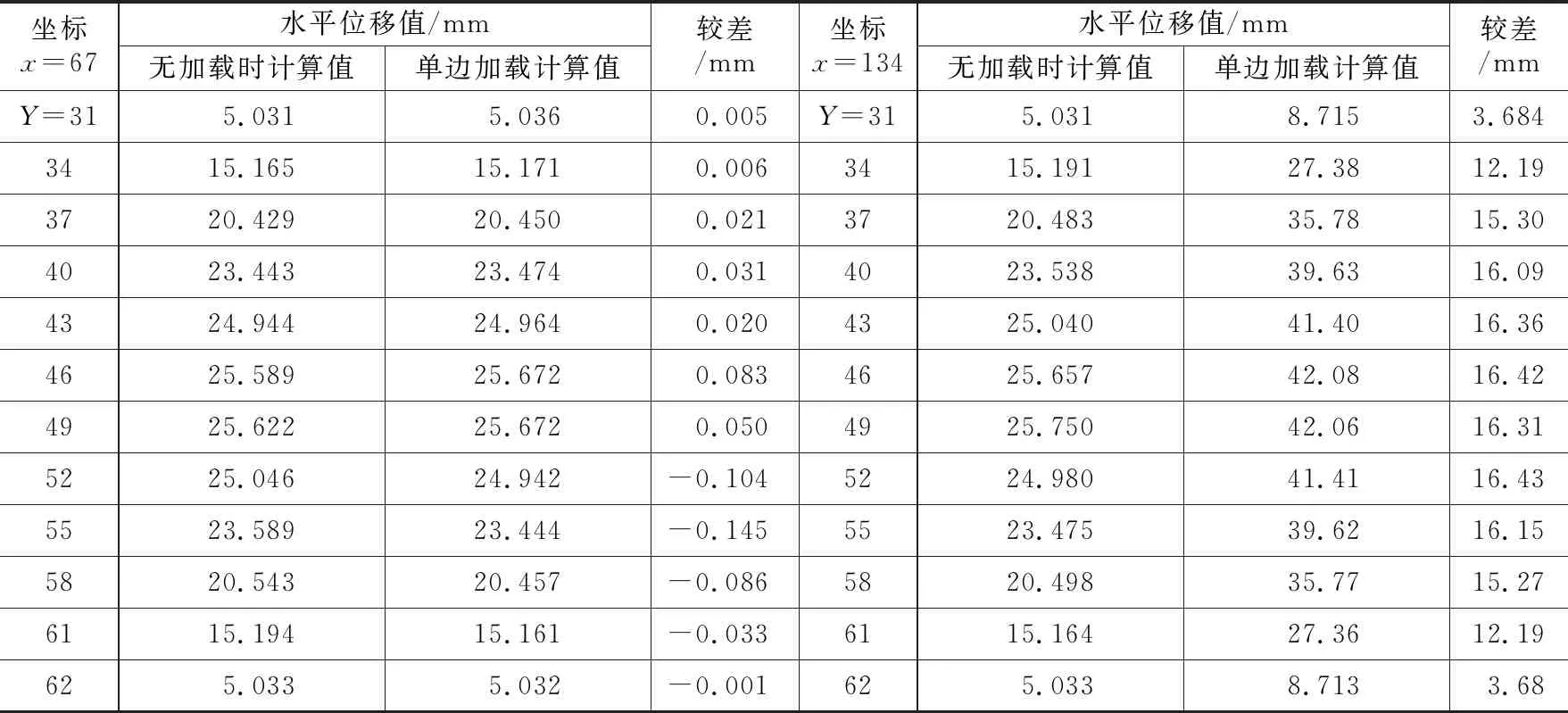
短边水平位移对比表 表3

通过对比，可以看出未加载的基坑边(X=67)，其顶部各点水平位移与无荷载情况下的基坑顶部各点水平位移比较变化不大；加载基坑边上(X=134)，其顶部各点水平位移比无荷载时增加较多，在所加载的短边中点上水平位移增加了 16.42 mm，增幅为63.9%。水平位移变化趋势与无荷载时一致，基坑顶部各点水平位移由基坑中部的最大值对称地向两边递减。

3.4 单边局部加载情况下变形模拟

本文选择深基坑施工荷载作为模拟的加载形式，加载条件设定情况如下：

(1)强度的确定：本文加载强度取 30 kPa，由《建筑施工手册》堆土要求反算而来。

(2)长度的确定：本文加载长度取 9.0 m，即基坑边缘至1倍开挖深度的位置。

(3)宽度的确定：本文加载宽度设为0.1L～0.5L(L为基坑边长)。

(4)位置的确定：本文加载位置分为从角点开始至宽度范围、以转折点为对称点、基坑中点开始偏离中点至角点方向的宽度范围。

为对比不同状态下的位移情况，本文分别以0.1L～0.5L的不同宽度在不同位置加载等13种工况进行模拟。模拟工况如下(表4)：

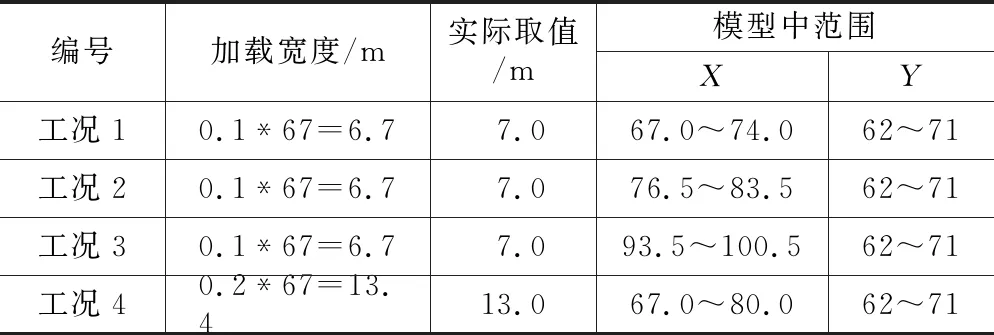
短边水平位移对比表 表4

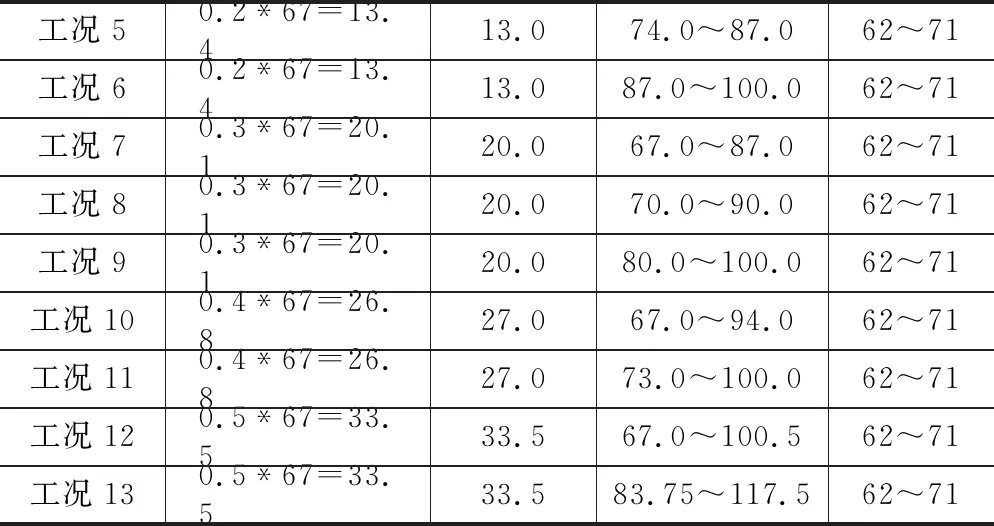
续表4

在不同工况下模拟，将模拟计算与测量数据比较，可以对比出局部施加荷载情况下的变形情况。由于工况较多，无法一一列举，限于篇幅，本文仅列出固定了位置但变换加载宽度的几个工况(工况3、6、9、12、14)水平位移对比图(图5)，以及固定了宽度但变换加载位置的几个工况(工况12、13)水平位移对比图(图6)。

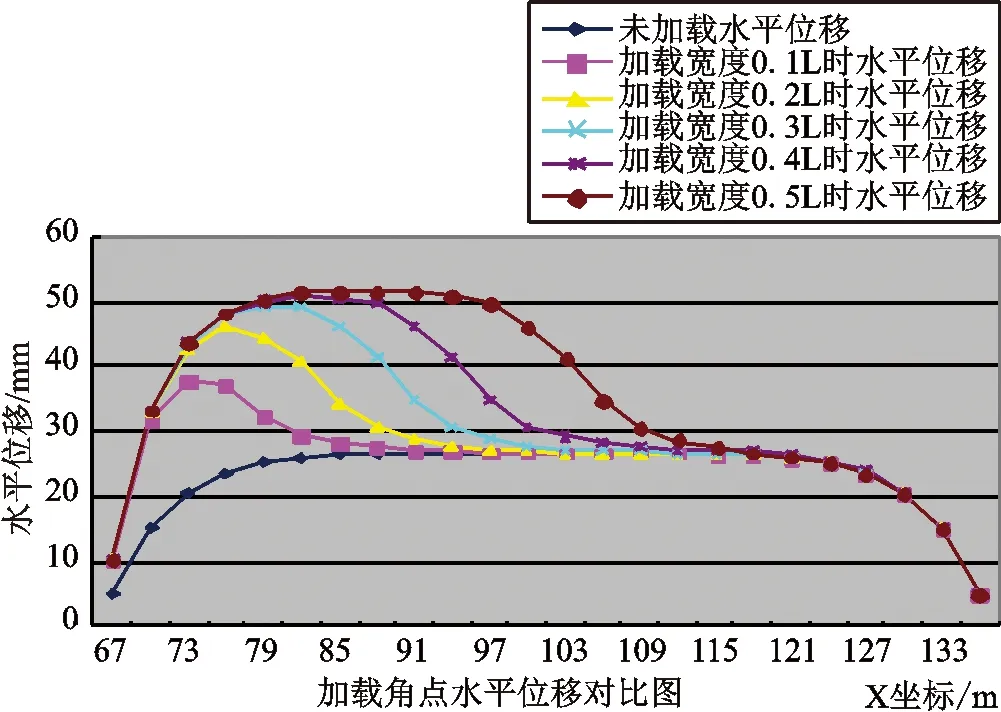
图5 荷载位于基坑角点时不同宽度下的水平位移对比图

图6 加载宽度0.4L时水平位移对比图

通过多种工况的对比分析可以看出，对于角点之外的位置进行加载，在位置不变的情况下，加载宽度越大则水平位移最大值也越大，水平位移最大值与荷载中心位移值差异变小，荷载影响范围的绝对值变大，但影响范围与加载宽度的比值变小；在加载宽度不变时，随着加载中心与基坑中部距离减小，水平位移最大值与荷载中心位移值差异变小，荷载中心位置与水平位移最大值位置差异变小，荷载影响范围变大，并逐渐趋于稳定；位于荷载中心的部分水平位移值增大得最多。

对于在角点处加载的情况，荷载对基坑顶部最大水平与荷载中心位移值及其位置影响较大；随着加载范围的增大，基坑顶部最大水平位移变大，基坑顶部最大水平位移偏离加载中心的距离变小。

4 结 语

本文在实际案例测量数据的基础上，应用有限差分法对基坑边上无荷载、单边满布荷载、单边局部荷载几种情况下基坑顶部各点水平位移分布情况进行了数值模拟分析与计算，通过计算可以看出在参数准确的情况下，模拟计算能较好地预测基坑边变形趋势。这种模拟计算可以用来指导水平位移监测点的设置。以本文的案例来说，在单边加载的情况下，如果加载位于基坑角点范围以外，宜在荷载中心设置水平位移监测点；如果加载位置在基坑角点范围以内则还要结合加载宽度综合考虑来确定水平位移监测点的设置位置。此外，模拟计算还可以指导施工荷载安放位置。若基坑边存在不可避免的施工荷载情况下，可以将施工荷载放置于从基坑边起的1倍基坑开挖深度范围之外；若因客观条件必须放置于1倍开挖深度范围之内，建议荷载放置于基坑四个角落的角点范围内。